美しすぎる 数と級数と積分と
今回、この記事に内容が詰まってしまい、証明や導出などを畳み込んであります。(フェルマー的なことを言って誤魔化してもよかったのですが、さすがにプライドが許さなかったです^^)
畳み込まれている部分は、このように強調された書体となっておりますので、閲覧の際はご注意ください。
初めに
こんにちは。にわかの数学好きArsenicです!
今回は、mathlog様の公式のイベントに参加させていただきましたが、まだ2記事目なので、甘めにお願いいたします!
今回は、数学の定数の中でも「美しい」、「重要だ」と呼ばれることの多い
$ \color {red}\pi(円周率)$、$\color {purple} e(自然対数の底)$、$\color {orange} \gamma(オイラー定数)$、$\color{magenta} i(虚数単位)$、$\color{green} \phi(黄金比)$
に関して積分や級数(+微分方程式)で語り尽くしたいと思います。
簡単に内容を載せますと、
1) 数の評価
2) 積分厳選11問
3) 物理、化学と精通する数
という感じです。
少し難しい内容もありますが、美しいので是非!
$\color{red}\pi$に関して
$\color{red}\pi$は、言わずと知れた数「円周率」です。
様々な定義の仕方がありますが、有名な近似でいえば、$$\int_{0}^{1} \dfrac{1}{x^2+1} dx=\dfrac{\color{red}\pi}{4} $$$$4\arctan\dfrac{1}{5}-\arctan\dfrac{1}{239}=\dfrac{\color{red}\pi}{4}(マチンの公式)$$$$\int_{-\infty}^{+\infty} \dfrac{\sin x}{x} dx=\color{red}\pi$$などがあげられます。
$\color{purple}e$関して
$\color{purple}e$も有名な数である、「自然対数の底」です。(ネイピア数とも言います)
$\color{purple}e$の定義式も様々な形がありますが、$$\color{purple}
e = \lim_{t \to 0} (1 + t)^{\frac{1}{t}}
$$
この定義式は非常に有名です。
$\color{orange}\gamma$関して
$\color{orange}\gamma$は、「オイラー定数」と呼ばれ、$$\color{orange}\gamma=\lim_{n \to \infty} \left(1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots +\dfrac{1}{n}-\log n\right)$$で定義されます。
しかしながら、この定数が有理数なのか無理数なのかもわかっていません。
$\color{magenta} i $に関して
$\color{magenta} i $は、虚数単位といい、$ \sqrt{-1}$ に値する数です。
様々な応用例があるわけではない(僕の知識不足)ですが、有名な式として、$$\color{purple} {e}^{\color{magenta}{i} \color{red} {\pi}}\color{black}=-1$$は非常に有名です。
$\color{green} \phi$に関して
$\color{green} \phi$ は、黄金比(黄金数)と呼ばれる数で、二次方程式$$x^2-x-1$$
の解です。
特殊関数の紹介
ここで、いくつか特殊関数を紹介しておきます。(最後のはマニアックですが、あとで出てきます^^)
$Beta Function$
$\Re (x)>0、\Re (y)>0$なる複素数$x、y$に対して、
$$\color{blue} B(x,y)=\int_{0}^{1} t^{x-1} (1-t)^{y-1} dt$$
$Gamma Function$
$x \notin {0、1、2 \cdots}$なる複素数$x$に対して、
$\begin{eqnarray}
\left\{
\begin{array}{l}
\color{brown}\Gamma(x)=\int_0^{\infty} t^{x-1} {\color{purple} {e}} ^{-t} dt (\Re(x)>0) \\
\color{brown} \Gamma(a)=\dfrac{\Gamma(a+1)}{a}が成り立つ (\Re(x)<0)
\end{array}
\right.
\end{eqnarray}$
$Dirichlet's Eta Function$
$$\color{olive} \eta(x)=\sum_{n=1}^{\infty} \dfrac{(-1)^{n-1}}{n^s}$$
また、ガンマ関数の亜種として、「ディガンマ関数」というものが存在し、通常、$\psi(z)$であらわされます。
ディガンマ関数は、ガンマ関数を対数微分して得られる関数で、性質として、$\psi(1)=-\gamma$というものがあります。
積分であらわしてみる。
これらの美しい定数ですが、面白い積分があるので、ご紹介したいと思います。
$$\int_{-\infty}^{+\infty} \dfrac{\cos x}{1+x^2} dx=\dfrac{\color{red}\pi}{\color{purple}e}$$
$$\int_{0}^{\infty} \dfrac{\sin x \log x}{x} dx=-\dfrac{\color{orange}\gamma \color{red}\pi}{2}$$
これらが成り立ちます。(勿論示します。)
一個目の積分
被積分関数を$I$とおく。この時、$$I=2\int_{0}^{\infty} \dfrac{\cos x}{x^2+1} dx$$
ここで、$$I(t)=\int_{0}^{\infty} \dfrac{\cos tx}{x^2+1}$$を考える。
ラプラス変換すると、
$$\mathcal{L} \left( I(t)\right)=\int_{0}^{\infty} e^{-st} I(t) dt$$
$$\int_{0}^{\infty} e^{-st} \int_{0}^{\infty} \dfrac{\cos tx}{x^2+1} dxdt$$
ここで、最初の積分は、独立しているから、$$\to \int_{0}^{\infty} \int_{0}^{\infty} e^{-st} \dfrac{\cos tx}{x^2+1} dxdt$$
フビニの定理を用いて、
$$\int_{0}^{\infty} \int_{0}^{\infty} e^{-st} \dfrac{\cos tx}{x^2} dtdx$$
$$=\int_{0}^{\infty} \dfrac{1}{x^2+1} \left( \int_{0}^{\infty} e^{-st} \cos tx dt\right)dx$$
()中は、$\cos tx$のラプラス変換であるから、
$$\mathcal{L}\left( I(t)\right)=\int_{0}^{\infty} \left( \dfrac{1}{x^2+1} \dfrac{s}{s^2+x^2}\right) dx$$
ここで、部分分数分解を行うと、$$\dfrac{s}{\left( x^2+1\right)\left(s^2+x^2\right)}=\dfrac{s}{s^2-1}\left( \dfrac{1}{x^2+1} -\dfrac{1}{x^2+s^2}\right)$$
$$\int_{0}^{\infty} \dfrac{s}{\left( x^2+1\right)\left(s^2+x^2\right)}=\dfrac{s}{s^2-1}\int_0^{\infty}\left( \dfrac{1}{x^2+1} -\dfrac{1}{x^2+s^2}\right) dx$$
以上より、$$\mathcal{L} \left( I(t)\right) =\dfrac{s}{s^2-1}\left[ \arctan x-\dfrac{1}{s} \arctan \dfrac{x}{s}\right]_{0}^{\infty}$$
$$=\dfrac{s}{s^2-1}\left( \dfrac{{\color{red} \pi}}{2} -\dfrac{1}{s} \dfrac{{\color{red} \pi}}{2}\right)$$
$$=\dfrac{{\color{red} \pi}}{2} \dfrac{s}{s^2-1}\left( \dfrac{s-1}{s}\right)$$
$$\mathcal{L}\left( I(t)\right)= \dfrac{{\color{red} \pi}}{2} \dfrac{1}{s+1}$$
$$\to \mathcal{L}^{-1} \mathcal{L}\left( I(t)\right)= \mathcal{L}^{-1}\left(\dfrac{{\color{red} \pi}}{2} \dfrac{1}{s+1}\right)$$
$$=I(t)=\dfrac{{\color{red} \pi}}{2} e^{-t}$$
$$\therefore I=I(1)=\dfrac{{\color{red} \pi}}{e}$$
考察していきます。
この積分は、留数定理を用いれば、簡単に示せるかもしれません(確証はないですが)
この記事の最初のほうでラプラス変換という操作が出てきました。
様々な変換をした後に、結果的に$e$という数に収束(数学的な意味ではない)するのは結構美しいことだと思います。
また、三角関数などの定積分の計算では、よく${\color{red} \pi}$などが登場します。(弧度法でもそうですね。)
$\arctan$の$0$から、$\infty$までの定積分の値は、$\frac{{\color{red} \pi}}{2}$になるものも一つの魅力だと思います。
二個目の積分
被積分関数を$I$とおく。
まず、$$ I(s)=\int_{0}^{\infty} \dfrac{\sin x}{x^s}$$ を考える。
$$\dfrac{d}{ds} I(s)=\dfrac{d}{ds} \int_{0}^{\infty} \dfrac{\sin x}{x^s} dx$$
$$=\int_{0}^{\infty} \dfrac{\partial}{\partial s} \dfrac{\sin x}{x^s} dx$$
$$\dfrac{\partial}{\partial s} x^{-s}= x^{-s} \log x$$より、
$$I'(s)=\int_{0}^{\infty} \dfrac{\sin x}{x^s} \log x dx$$
今回、$I'(s=1)=I$である。
$$I(s)=\int_{0}^{\infty} \dfrac{\sin x}{x^s}$$
$$=\int_{0}^{\infty} \sin x \dfrac{1}{x^s}$$
ここで、$$I_1=\int_{0}^{\infty} t^{-s-1} e^{-tx} dt$$とする。
$tx=u\to dt=\frac{1}{x} du$より、$$I_1=\int_{0}^{\infty} \dfrac{u^{s-1}}{x^{s-1}} e^{-u} \dfrac{du}{x}$$
$$=\dfrac{1}{x^s} \int_{0}^{\infty} u^{s-1} e^{-u} du=\dfrac{1}{x^s} \Gamma(s)$$
$$\to \dfrac{1}{x^s} =\dfrac{1}{\Gamma(s)} \int_{0}^{\infty} t^{s-1} e^{-tx} dt$$
$$\to I(s)=\int_{0}^{\infty} \sin x\left( \dfrac{1}{\Gamma(s)} \int_{0}^{\infty} t^{s-1} e^{-tx} dt\right) dx$$
$$=\dfrac{1}{\Gamma(s)} \int_{0}^{\infty} \int_{0}^{\infty} \left(\sin x\right) t^{s-1} e^{-tx} dxdt$$
$t$は独立しているから、
$$=\dfrac{1}{\Gamma(s)} \int_{0}^{\infty} t^{s-1} \left( \int_{0}^{\infty} \sin x e^{-tx} dx\right) dt$$
$$I(s)=\dfrac{1}{\Gamma(s)} \int_{0}^{\infty} \dfrac{t^{s-1}}{1+t^2} dt$$
ここで、$t^2=y \to dt=\frac{1}{2} y^{-\frac{1}{2}} dy$と置換すると、
$$I(s)=\dfrac{1}{2\Gamma(s)} \int_{0}^{\infty} \dfrac{y^{\frac{s-1}{2}}y^{-\frac{1}{2}}}{1+y}$$
$$I(s)=\dfrac{1}{2 \Gamma(s)} \int_{0}^{\infty} \dfrac{y^{\frac{s}{2}-1}}{1+y}$$
ここで、$$\int_{0}^{\infty} \dfrac{y^{z-1}}{1+y}=\Gamma(z)\Gamma(1-z)={\color{red} \pi} \csc {\color{red} \pi} z$$だから、
$$I(s)=\dfrac{1}{2 \Gamma(s)} {\color{red} \pi} \csc\dfrac{{\color{red} \pi} s}{2}$$
ここで、$I=I'(s=1)$だから、
$$I'(s)=\dfrac{{\color{red} \pi}}{2} \left( \dfrac{-\Gamma'(s)}{\Gamma^2(s)} \csc\dfrac{{\color{red} \pi} s}{2} -\dfrac{{\color{red} \pi}}{2} \csc\dfrac{{\color{red} \pi} s}{2} \cot \dfrac{{\color{red} \pi} s}{2}\right)$$
$$\to I'(1)=\dfrac{{\color{red} \pi}}{2} \left( \Gamma'(1) \csc\dfrac{{\color{red} \pi}}{2} -\dfrac{{\color{red} \pi}}{2} \csc\dfrac{{\color{red} \pi}}{2} \cot \dfrac{{\color{red} \pi}}{2}\right)$$
$$=I'(1)=-\dfrac{{\color{red} \pi}}{2} \Gamma'(1)$$
$$\therefore I'(1)=I=-\dfrac{{\color{red} \pi} \gamma}{2}$$
考察していきます。
ガンマ関数の反射公式である$refrection formula$が登場しました。
この公式を使用したら、必ず$\pi$と、三角関数の一つである$\csc$が登場しました。この時点で、もうその積分に$\pi$が登場することが決まったもの 的な感じに感じますが、今回は、オイラー定数$\gamma$が登場したことも一つの魅力です。
先ほど、ガンマ関数の亜種として紹介いたしました、「ディガンマ関数」と、オイラー定数$\gamma$に関係があることも不思議です。
「ディガンマ関数」が、ガンマ関数を(対数)微分することによって得られる関数であるから、先ほどのように関数$I(s)$のようなものを考え、変換していく過程で、ガンマ関数を微分する必要性が出てきて、その際にディガンマ関数になり、オイラー定数が登場する。こんな感じの流れですね。
また、あくまでも余談ですが、二項係数とも面白いつながりがあり、
$$ \color {blue}\lim_{n \to \infty} \sqrt[2^n]{\prod_{k=0}^{n} {}_n \mathrm{C}_k}=\sqrt{\color{purple}e}$$という等式も成り立ちます。(これは示しましょう。)
区分求積で証明
$$\lim_{n \to \infty} \sqrt[2^n]{\prod_{k=0}^{n} {}_n \mathrm{C}_k}=\lim_{n \to \infty} \left( \left(n!\right)^{n+1}\left(\prod_{k=0}^{n} \dfrac{1}{k!}\right)^2\right)^{\frac{1}{n^2}}$$
$$=\lim_{n \to \infty} \left( (n!)^{n+1} \prod_{k=1}^{n} \prod_{i=1}^{k} \dfrac{1}{i^2} \right)^{\frac{1}{n^2}}$$
$$=\lim_{n \to \infty} \left( \prod_{i=1}^n i^{n+1} \cdot \prod_{i=1}^n \dfrac{1}{(i^2)^{n+1-i}} \right)^{\frac{1}{n^2}}$$
$$=\lim_{n \to \infty} \left(\prod_{i=1}^{n} i^{2i-n-1}\right)^{\frac{1}{n^2}}$$
$$=\lim_{n \to \infty} \exp{\dfrac{1}{n^2} \sum_{i=1}^{n} \left(2i-n-1\right) \log i}$$
$$=\lim_{n \to \infty} \exp{\left( \dfrac{1}{n^2} \sum_{i=1}^{n} \left( 2i-n-1\right) \left( \log i - \log n\right)\right)} $$
ここで、$$\sum_{i=1}^{n} \left( 2i-n-1\right)=0$$
であるから、$$=\lim_{n \to \infty} \exp {\left( \dfrac{1}{n} \sum_{i=1}^{n} \left(\dfrac{2i}{n}-1-\dfrac{1}{n}\right) \log {\dfrac{i}{n}} \right)}$$
$$=\exp{\int_0^1 \left( 2x-1\right) \log x dx}$$
$$=\color{purple} {e} ^{\color{black}\frac{1}{2}}=\color{black}\sqrt{\color{purple} e}$$
さて、今回の記事では、様々なことをやってみたい思います。
というわけで、まずはこちら!
$ \dfrac{\color{red}\pi}{\color{purple}e^{\color{orange}\gamma}}$の考察
$$A=\dfrac{\color{red}\pi}{\color{purple}e^{\color{orange}\gamma}} $$
を考えてみます.
なかなか一筋縄ではいかなさそうなゴツイ(あくまでも僕の感想です)ですが、考察してみましょう.
適当に近似すると、
$$\dfrac{\pi}{e^{\gamma}}≒1.763876989\cdots$$
です。
導出は以下です。
ただの計算
まず、$\gamma$を導出する。
オイラー-マクローリンの総和公式を用いる。
オイラーマクローリンの総和公式は、
$f(x)$を、$(2m+1)$階連続微分可能な関数とすると、
$$\sum_{k=1}^{n} f(k)=\int_{0}^{n} f(x) dx+\dfrac{1}{2} \left( f(1)+f(n)\right) +\sum_{k=1}^{m} \dfrac{B_{2k}}{(2k)!} \left( f^{(2k-1)} (n) -f^{(2k-1)} (1) \right)+R_{n} (f、m)$$
ただし、$$0≦R_{n} (f、m)≦\dfrac{2}{(2\pi)^{2m} } \int_{1}^{n} |f^{(2m+1)} (x)| dx$$は剰余項、$B_{2k}$はベルヌーイ数である。
これを用いて、オイラー定数の近似値を求めます。
まず、$f(x)=\frac{1}{x}$を求めると、
$$f'(x)=-\dfrac{1}{x^2}、f''(x)=\dfrac{1}{x^3}\cdots f^{(n)}(x)=(-1)^n \dfrac{n!}{x^{n+1}}$$
これを先ほどの公式に適用すると、
$$\sum_{k=1}^{n} \dfrac{1}{k} =\log n+\dfrac{1}{2} \left( \dfrac{1}{1} +\dfrac{1}{n}\right)+\sum_{k=1}^{m} \dfrac{B_{2k}}{(2k)!} \left( (-1)^{2k-1} \dfrac{(2k-1)!}{n^{2k}} - (-1)^{2k-1} (2k-1)!\right) R_{n} (f、m)$$
ここで、$(2k)!=(2k-1)!\cdot 2k$から、
$$\sum_{k=1}^{n} \dfrac{1}{k} =\log n+\dfrac{1}{2} \left( \dfrac{1}{1} +\dfrac{1}{n}\right)+\sum_{k=1}^{m} \dfrac{B_{2k}}{2k} \left( 1-\dfrac{1}{n^{2k}}\right) R_{n} (f、m)$$
これを、オイラー定数の定義式に代入すると、
$$\gamma=\lim_{n \to \infty} \left(\log n+\dfrac{1}{2} \left( \dfrac{1}{1} +\dfrac{1}{n}\right)+\sum_{k=1}^{m} \dfrac{B_{2k}}{2k} \left( 1-\dfrac{1}{n^{2k}}\right) R_{n} (f、m) -\log n\right)$$
$$=\dfrac{1}{2} +\sum_{k=1}^{m}\dfrac{B_{2k}}{2k} +R_{\infty} (f、m)$$
以上より、
$$\sum_{k=1}^{n} \dfrac{1}{k} =\log n+\dfrac{1}{2} \left( \dfrac{1}{1} +\dfrac{1}{n}\right)+\sum_{k=1}^{m} \dfrac{B_{2k}}{2k} \left( 1-\dfrac{1}{n^{2k}}\right) R_{n} (f、m)$$
$$=\log n+\dfrac{1}{2n} -\dfrac{1}{2^{2k}} \sum_{k=1}^{m} \dfrac{B_{2k}}{2k} +R_{n} (f、m)-R_{\infty} +\left( \dfrac{1}{2} +\sum_{k=1}^{m} \dfrac{B_{2k}}{2k} R_{\infty} (f、m)\right)$$
この式の誤差項を無視して、$B_2、B_4、B_6\cdots B_{2n}$に値を代入することで、$$\gamma=\sum_{k=1}^{n} \dfrac{1}{k} -\log n -\dfrac{1}{2n}+\dfrac{1}{12n^2}-\dfrac{1}{120n^4}+\dfrac{1}{256n^6}+\cdots$$
個の級数を用いて、オイラーは、$\gamma$を少数第16位まで計算して、$$\gamma=0.5772156649015325\cdots$$をたたき出しました。
さて、せっかく求めたので、$\frac{\pi}{e^{\gamma}}$を近似してみましょう。
それぞれを少数16位まで用意します。
${\color{red} \pi}=3.1415926535897932\cdots$
$e=2.7182818284590452\cdots$
$\gamma=0.5772156649015325\cdots$だから、$$\dfrac{{\color{red} \pi}}{e^{\gamma}}≒1.763876989\cdots$$です。
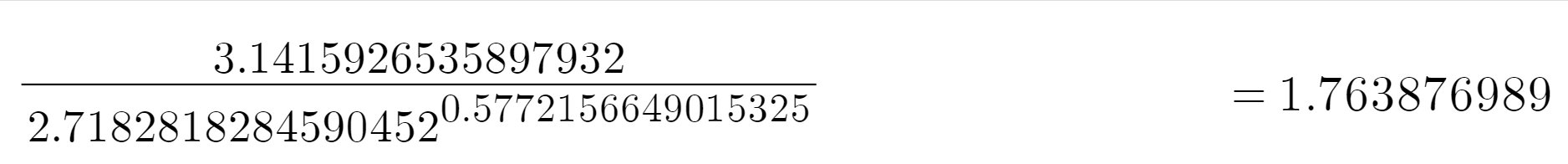電卓様の結果
積分です
$$I=\int_{0}^{1} \log \left(\log \dfrac{1}{x} \right) \dfrac{1}{\left( 1+x\right)^2} dx$$
まず、$\log x = -u \to x=e^{-u} \to dx=-e^{-u} dx$
したがって、積分は、$$I=\int_{0}^{\infty} \dfrac{\log u}{\left( 1+e^{-u}\right)^2} e^{-u} du$$
ここで、$u\to x$とすると、
$$I=\int_{0}^{\infty} \dfrac{\left( \log x\right)e^{-x}}{\left( 1+e^{-x}\right)^2} dx$$
ここで、$$\dfrac{1}{1+x} =\sum_{k≧0} (-1)^k x^k$$
$|x|<1$から、
$$\to \dfrac{1}{1+e^{-x}} =\sum_{k≧0} (-1)^k e^{-kx}$$
$$-\dfrac{(-e^{-x})}{(1+e^{-x})^2} =\sum_{k≧0} (-1)^{k} (-k)^{-kx}$$
$$=\sum_{k≧0} (-1)^{k+1} ke^{-kx}$$
$$I(s)=\int_{0}^{\infty} \dfrac{x^{s-1}e^{-x}}{(1+e^{-x})^2} dx$$
$$=I'(s)=\int_{0}^{\infty} \dfrac{\left( x^{s-1} \log x\right) e^{-x}}{(1+e^{-x})^2}$$
$I'(s=1)=I$となる。
$$\to \int_{0}^{\infty} x^{s-1} \dfrac{e^{-x}}{(1+e^{-x})^2} dx=\int_{0}^{\infty} x^{s-1} \sum_{k≧1}(-1)^{k+1} ke^{-kx} dx$$
$$\int_{0}^{\infty}=\sum_{k≧1} (-1)^{k+1} k\int_{0}^{\infty} x^{s-1} e^{-kx} dx$$
ここで、$kx=u \to x=\frac{du}{k}$
$$\to I(s)=\sum_{k≧1} (-1)^{k+1} k\int_{0}^{\infty} \dfrac{u^{s-1}}{k^{s-1}} e^{-u} \dfrac{du}{k}$$
$$=\sum_{k≧1} \dfrac{(-1)^{k+1}}{k^{s-1}} \int_{0}^{\infty} u^{s-1} e^{-u} du$$
上の式の後半は、ガンマ関数である。
$$=\Gamma(s) \sum_{k≧1} \dfrac{(-1)^{k+1}}{k^{s-1}}$$
後半は、ディリクレのイータ関数だから、
$$=\Gamma(s) \eta(s)$$
$$I'(s)=\Gamma'(s) \eta(s-1)+\Gamma(s) \eta'(s-1)$$
今回は、$I(1)$だから、
$$I=\Gamma'(1) \eta(0)+\eta'(0)$$
ここで、$$\Gamma'(1)=-\gamma、\eta(0)=\dfrac{1}{2}、\eta'(0)=\dfrac{1}{2} \log \dfrac{{\color{red} \pi}}{2}$$であるから、
$$I=\dfrac{\gamma}{2} +\dfrac{1}{2} \log \dfrac{{\color{red} \pi}}{2}$$
$$I=\dfrac{1}{2} \left( -\gamma+\log \dfrac{{\color{red} \pi}}{2}\right)$$
ここで、$-\gamma=\log e^{\gamma}$だから、$$I=\dfrac{1}{2} \left( \log \dfrac{{\color{red} \pi}}{2} -\log e^{\gamma}\right)$$
$$\therefore I=\dfrac{1}{2} \log \dfrac{{\color{red} \pi}}{2e^{\gamma}}$$
らまぬじゃん
$$\int_{0}^{\infty} e^{-\alpha e^x}+e^{-\alpha e^{-x}} -1 dx (\alpha>0)$$
積分を$I(\alpha)$とおく。
$x \to -x$とすると、$$I(\alpha)=\dfrac{1}{2} \int_{-\infty}^{\infty} e^{-\alpha e^x}+e^{-\alpha e^{-x}} -1 dx$$
ここで、$e^{x}=u\to x=\log u\to dx=\frac{1}{u} du$から、
$\alpha\to -\infty、u \to 0$
$\alpha \to \infty、u \to \infty$だから、
$$I(\alpha)=\dfrac{1}{2} \int_{0}^{\infty} \left( e^{-\alpha x} +e^{-\frac{\alpha}{u}}-1\right) \dfrac{1}{u} du$$
$$=\dfrac{1}{2}\left( \int_{0}^{\frac{1}{\alpha}} +\int_{\frac{1}{\alpha}}^{\infty} \dfrac{e^{-\alpha x} +e^{-\frac{\alpha}{u}}-1}{u} du\right)$$
ここで、$$I_1=\int_{0}^{\frac{1}{\alpha}} \dfrac{e^{-\alpha u}-1}{u} du+\int_{\frac{1}{\alpha}}^{\infty} \dfrac{e^{-\alpha u}}{u} du$$
$$I_2=\int_{0}^{\frac{1}{\alpha}} \dfrac{e^{-\frac{\alpha}{u}}}{u}du+\int_{\frac{1}{\alpha}}^{\infty} \dfrac{e^{-\frac{\alpha}{u}}-1}{u} du$$
とする。
まず、$I_1$を求める。
ここで、$\alpha u=z$とおく。$\to du=\frac{1}{\alpha} dz$
だから、
$$I_1=\int_{0}^{1} \dfrac{e^{-z}-1}{z} \alpha \dfrac{1}{\alpha} dz+\int_{1}^{\infty} \dfrac{e^{-z}}{z} \alpha \dfrac{1}{\alpha} dz$$
$$=\int_{0}^{1} \dfrac{e^{-z}-1}{z} dz+\int_{1}^{\infty} \dfrac{e^{-z}}{z} dz$$
したがって、$I_1=-\gamma$
$I_2$を求める。
まず、$\frac{\alpha}{u}=z\to u=\frac{\alpha}{z} \to du=-\frac{\alpha}{z^2} dz$から、
$$I_2=\int_{\infty}^{\alpha^2} \dfrac{e^{-z}}{\alpha} z\dfrac{-\alpha}{z^2} dz+\int_{\alpha^2}^{0} \dfrac{e^{-z}-1}{\alpha} z\left(\dfrac{-\alpha}{z^2} \right) dz$$
$$I_2=\int_{\infty}^{\alpha^2} \dfrac{e^{-z}}{z} dz+\int_{0}^{\alpha} \dfrac{e^{-z}-1}{z} dz$$
$$=\int_{\infty}^{\alpha^2} \dfrac{e^{-z}}{z} dz+\int_{0}^{\alpha^2} \dfrac{e^{-z}}{z} dz-\int_{0}^{\alpha^2} \dfrac{1}{z^2} dz$$
したがって、
$$I_2=\int_{0}^{\infty} \dfrac{e^{-z}}{z} dz-\int_{0}^{\alpha^2} \dfrac{1}{z} dz$$
$$=\int_{0}^{1} \dfrac{e^{-z}}{z} dz+\int_{1}^{\infty} \dfrac{e^{-z}}{z} dz-\int_{0}^{1} \dfrac{1}{z} dz-\int_{1}^{\alpha^2} \dfrac{1}{z} dz$$
$$=\int_{0}^{1} \dfrac{e^{z-1}}{z} dz+\int_{1}^{\infty} \dfrac{e^{-z}}{z} dz-\int \dfrac{1}{\alpha^2} \dfrac{1}{z} dz$$
$$=-\gamma-\left. \log z\right|_{1}^{\infty}$$
$$\therefore I_2=-\gamma-2\log \alpha$$
以上より、$I_1=-\gamma、I_2=-\gamma-2\log \alpha$より、
$$I(\alpha)=\dfrac{1}{2}\left( -2\gamma-2\log \alpha \right)$$
$$\therefore I(\alpha)=-\left( \gamma+\log \alpha \right)$$
ここから、値を入れていく。
$$I({\color{red} \pi})=-(\gamma+\log {\color{red} \pi})=-(\log e^{\gamma} +\log {\color{red} \pi})$$
$$\therefore I(\pi)=-\log e^{\gamma} {\color{red} \pi}$$
$$I(\gamma)=-\log e^{\gamma} \gamma$$
$$I(\phi)=-\log e^{\gamma} \phi$$
$$I(e^{-69})=69-\gamma$$
ガンマ関数の
ガンマ関数の評価
$$\dfrac{1}{\Gamma(x)}=xe^{\gamma x} \prod_{k≧1} \left( 1+\dfrac{x}{k}\right)e^{-\frac{x}{k}}$$
$$-\log \Gamma(x)=\log x+\log e^{\gamma x}+\sum_{k≧1}\log \left( 1+\dfrac{x}{k}\right)e^{-\frac{x}{k}}$$
$$\to -\log \Gamma(x)=\log x+\gamma x+\sum_{k≧1}\log \left( 1+\dfrac{x}{k}\right)e^{-\frac{x}{k}}$$
$$\to -\log \Gamma(x+1)=\gamma x +\sum_{k≧1} \left(\log \left(1+\dfrac{1}{k}\right)-\dfrac{x}{k} \right)$$
$$\to \log \Gamma(x+1)=-\gamma x+\sum_{k≧1}\left( \dfrac{x}{k} -\log \left(1+\dfrac{x}{k}\right)\right)$$
ここで、
$$\dfrac{1}{x+1} =\sum_{n≧1} (-1)^{n-1} x^{n-1} (|x|<1)$$
これの積分を考えると、
$$\int \dfrac{1}{x+1} =\int \sum_{n≧1} (-1)^{n-1} x^{n-1}$$
$$\to \log \left( 1+\dfrac{x}{k}\right)=\sum_{n≧1} (-1)^{n-1} \dfrac{x^n}{k^n n}$$
$$\to \log \Gamma(x+1)=-\gamma x +\sum_{k≧1} \left( \dfrac{x}{k}-\sum_{n≧1} \dfrac{(-1)^{n-1} x}{k^n n}\right)$$
$$=-\gamma x+\sum_{n≧1} \left( \dfrac{x}{k}-\dfrac{x}{k}-\sum_{k≧2} \dfrac{(-1)^{n-1} x}{k^n n}\right)$$
$$\log \Gamma(x+1)=-\gamma x-\sum_{k≧1} \sum_{n≧2} \dfrac{(-1)^{n-1} x^n}{k^n n}$$
ここで、総和記号に関して、この級数は収束するから、
$$=-\gamma x -\sum_{n≧2} \sum_{k≧1} \dfrac{(-1)^{n-1} x^n}{k^n n}$$
$$=-\gamma x-\sum_{n≧2} \dfrac{(-1)^{n-1} x^n}{n} \sum_{k≧1} \dfrac{1}{k^n}$$
後ろの級数は、$\zeta(n)$だから、
$$\log \Gamma(x+1)=-\gamma x-\sum_{n≧2} \dfrac{(-1)^{n-1} x^n \zeta(n)}{n}$$
ここで、$x=-\frac{1}{2}$の時、
$$\log \Gamma\left( \dfrac{1}{2}\right)=\dfrac{\gamma}{2} -\sum_{n≧2} (-1)^{n-1} \left(\dfrac{1}{2} \right) (-1)^n$$
$$\to \log \Gamma \left( \dfrac{1}{2}\right)=\dfrac{\gamma}{2}-\sum_{n≧2} (-1)^{2n-1} \left( \dfrac{1}{2}\right)$$
$$=\dfrac{\gamma}{2}+\sum_{n≧2} \dfrac{\left( \dfrac{1}{2}\right)^n \zeta(n)}{n}$$
後ろの級数を$S$とでも置き、様々な値を代入すると、
$$\log \sqrt{{\color{red} \pi}}=\log e^{\frac{\gamma}{2}} +S$$
$$\to S=\log \sqrt{{\color{red} \pi}}-\log \sqrt{e^{\gamma}}$$
$$=\log \sqrt{\dfrac{{\color{red} \pi}}{e^{\gamma}}}$$
$$S=\dfrac{1}{2} \log \dfrac{{\color{red} \pi}}{e^{\gamma}}$$
微調整すると、
$$\sum_{n≧2} \dfrac{\zeta(n)}{2^{n-1} n}=\log \dfrac{{\color{red} \pi}}{e^{\gamma}}$$
複素対数関数
ここで、次の積分に行く前に、(正直言ってあまり使いませんが)定義したい事柄があるので定義します。
それは、$\color{magenta} i乗$の定義です。
例えば、非常に有名ですが、$\color{magenta} i^i$は実数になります。(この証明一応あげておきます)
$\color{magenta} i^i$は実数
複素対数関数を軽く定義します。
以下、$a、b \in \mathbb{R}、n \in \mathbb{Z}$とする。
この時、自然対数の底$\color{purple}e$に対して、$$\color{purple} e^{\color{black}z}=\color{purple} e^{\color{black}a}\color{black}\left( \cos b+\color{magenta} i \color{black}{\sin x}\right)$$
が成り立つ。
これの逆関数として、
複素数$z$が与えられたときに、$\color{purple} e^{\color{black}w}\color{black} = z$となる$w$を、$z$の対数とみなし、$w=\log z$で書く。
一般に、$0$でない複素数$z$に対して、その対数は、$$\log z=\log|z|+i\arg z$$
これらを用いると、複素数乗が定義できる。
ここから$\color{magenta} i^i$を評価する。
まず、複素対数関数は、多価関数であるため、範囲を$-\pi<\arg z≦\arg \pi$の範囲に限定すると、一つ取り出すことができます。
この値を「主値」といい、通常、$\mathrm{Log} z$として表現されます。
以上の道具を用いると、$\mathrm{log} i=\left( \frac{1}{2}+2n\right) \pi i$でありますから、範囲を$-\pi<\arg z≦\arg \pi$に限定すると、$\mathrm{Log} z=\dfrac{1}{2} {\color{red} \pi} i$
このことを用います。
まず、定義より、$i^i=e^{i \log i}$
そして、$\log i$の主値は、$\mathrm{Log} z=\dfrac{1}{2} {\color{red} \pi} i$から、$i^i=e^{\frac{1}{2} {\color{red} \pi} i^2 }$
以上から、$i^i=e^{-\frac{1}{2} \pi}=0.20787957635\cdots$
以上より、$i^i \in \mathbb{R}$が示された。
さて、上の定義を用いると、次のような積分
$$\int_{0}^{\frac{\pi}{2}} \tan^{\color{magenta} i} dx (\color{magenta}i\color{black}は虚数単位)$$
を見ても、吐きたくなりません。(まぁこの積分解くのには使わないのですが..)
ということで、へんてこりんな積分を計算します。
へんてこりんな積分
この積分を$I$と置くと、
$$I=\int_{0}^{\frac{\pi}{2}} \tan^{i} dx$$
まず、$\tan x=\sin x (\cos x)^{-1} $だから、
$$I=\int_{0}^{\frac{\pi}{2}} \sin^i \cos ^{-i} dx$$
$$=\left( \dfrac{1}{2}\right) 2\int_{0}^{\frac{\pi}{2}} \sin^i \cos ^{-i} dx$$
ここで、ベータ関数の定義$$B\left(x、y\right)=2\int_{0}^{\frac{\pi}{2}} \sin^{2x-1} t \cos^{2y-1} t dt$$から、
$$I=\dfrac{1}{2} B \left(\dfrac{1+i}{2}、\dfrac{1-i}{2}\right)$$
ここで、ベータ関数とガンマ関数の関係式から、
$$\dfrac{1}{2} \dfrac{\Gamma\left( \dfrac{1+i}{2}\right) \Gamma\left( \dfrac{1-i}{2}\right)}{\Gamma\left( \dfrac{1+i}{2}+ \dfrac{1-i}{2}\right)}$$
ここで、ガンマ関数の反射公式から、$$\dfrac{1}{2}{\color{red} \pi} \csc\left[ {\color{red} \pi} \left( \dfrac{1+i}{2}\right)\right] =\dfrac{1}{2} \csc\left[\dfrac{{\color{red} \pi}}{2} +\dfrac{i{\color{red} \pi}}{2} \right] =\dfrac{{\color{red} \pi}}{2} \sec\left( \dfrac{i{\color{red} \pi}}{2}\right)$$
$$\therefore I=\dfrac{{\color{red} \pi}}{2} \mathrm{sech} \left( \dfrac{{\color{red} \pi}}{2}\right)$$
はい。ということで、次の積分です。
$${\color{lime}I}=\int_{0}^{\frac{\pi}{2}} \dfrac{\csc x\left(2\sin x\right)}{\sin x}dx$$
はい、この積分も特に何の変哲もないただの積分ですね。
最低でも$\color{red} \pi$が絡むということは容易に想像できますね。
面白くないので、ささっと示して、次の積分に行きましょう。
実は盲点ほんとに盲点
まず、$$I(a)=\int_{0}^{\frac{\pi}{2}} \dfrac{\csc(a\sin x)}{\sin x} dx$$を定義します。$(I(2)=I)$
$$\dfrac{d}{da}I(a)=\dfrac{d}{da}\int_{0}^{\frac{\pi}{2}} \dfrac{\csc(a\sin x)}{\sin x} dx $$
$$I'(a)=\int_{0}^{\frac{\pi}{2}} \dfrac{\partial}{\partial a} \dfrac{\csc(a\sin x)}{\sin x} dx$$
$$\int_{0}^{\frac{\pi}{2}} \dfrac{1}{\sin x}\dfrac{\sin x}{1+a^2 \sin^2 x} dx$$
$$I'(a)=\int_{0}^{\frac{\pi}{2}} \dfrac{dx}{1+a^2 \sin^2 x}$$
ここで、$x \to \frac{\pi}{2} -x$とすると、
$$I'(a)=\int_{0}^{\frac{\pi}{2}} \dfrac{dx}{1+a^2 \left(\sin\left(\frac{\pi}{2}-x\right)\right)^2}$$
$$I'(a)=\int_{0}^{\frac{\pi}{2}} \dfrac{dx}{1+a^2\cos^2 x}$$
$$I'(a)=\int_{0}^{\frac{\pi}{2}} \dfrac{\sec^2 x dx}{\left( 1+a^2 \cos^2 x\right) \cdot \sec^2 x} 神のような選択$$
$$I'(a)=\int_{0}^{\frac{\pi}{2}} \dfrac{\sec^2x dx}{\sec^2 x+a^2}$$
$$I'(a)=\int_{0}^{\frac{\pi}{2}} \dfrac{\sec^2 x}{\left(a^2+1\right) +\tan^2 x}$$
ここで、$\tan x=u$と置換すると、
$x=0\to u=0、x=\frac{\pi}{2}\to u=\infty、\sec^2 x dx=du$
$$I'(a)=\int_{0}^{\infty} \dfrac{du}{a^2+1+u^2}$$
$$I'(a)=\dfrac{1}{\sqrt{a^2+1}} \tan^{-1} \left.\dfrac{u}{\sqrt{a^2+1}} \right|_{0}^{\infty}$$
$$I'(a)=\dfrac{\pi}{2} \dfrac{1}{\sqrt{a^2+1}}$$
したがって、
$$\int I'(a) da=\dfrac{\pi}{2}\int\dfrac{1}{\sqrt{1+a^2}} da$$
$$I(a)=\dfrac{\pi}{2} \sinh^{-1} a+C(Cは積分定数)$$
$I(a=0)=0=\frac{\pi}{2} \sinh^{-1} 0+C$
だから、$C=0$
$I(a)=\dfrac{\pi}{2} \sinh^{-1} a$
$I(2)=\dfrac{\pi}{2} \sinh^{-1} 2$
ここで、$\sinh^{-1} x=\log\left(x+\sqrt{x^2+1}\right)$
$$\sinh^{-1} 2=\log \left( 2+\sqrt{5}\right)=\log\left( 1+1+\sqrt{5}\right)$$
である。したがって、
$${\color{lime}I}=\dfrac{\color{red}\pi}{2} \log \left( 1+2{\color{green} \phi}\right)$$
考察していきます。
この積分の最後のほうに、双曲線関数sinhsinhが登場しました。
そして、この逆関数を考えると、自然対数が登場する美しい式になり、そのxに、1を入れたら黄金比が出てくることは結構盲点です。
この積分を選んだ理由としては、黄金比の出方が美しかったこと と、自然対数の中に黄金比が登場したこと
この二つが大きな理由です。
さて、いかがでしたでしょうか。最後に黄金比を持ってくるのは多少強引すぎたかもしれませんが、黄金比が答えに出てきましたね。
どんどん行きましょう。次の問題は、こちらです!!!
$f'(x)=f^{-1} (x)を満たす関数f(x)を1つ求めよ。$
ちょっと積分からは離れました。この問題には、果たして、どのような数学定数が登場するのでしょうか。
黄金比
個の微分方程式を満たす$f$を求める。
$$f(x)=y=\alpha x^{\beta} (\alpha、\beta \in \mathbb{C})$$
これを考える。ひとまず微分すると、
$$\dfrac{dy}{dx}=\alpha \beta x^{\beta-1}$$になる。
$y=\alpha x^{\beta} \to \frac{y}{\alpha}=x^{\beta}$
以上より、$$y^{\frac{1}{\beta}} \alpha^{-\frac{1}{\beta}}$$
$$\therefore f^{-1}(x)=x^{\frac{1}{\beta}} \alpha^{-\frac{1}{\beta}}$$
$$f'=f^{-1} \to \alpha \beta x^{\beta-1} =\alpha^{-\frac{1}{\beta}} x^{\frac{1}{\beta}}$$
この$2$津が等しいということは、「係数と指数が等しい」ことだから、連立方程式
$$ \begin{cases} \beta-1=\dfrac{1}{\beta} \\ \alpha \beta=\alpha-\dfrac{1}{\beta} \end{cases} $$
となる。この連立方程式を解くと、$$\beta\left( \beta-1=\dfrac{1}{\beta}\right)$$
$$=\beta^2-\beta-1=0$$
$$\therefore \beta={\color{green} \phi}、1-{\color{green} \phi}$$
したがって、$$\alpha^{\frac{1}{\beta}}\left( \alpha \beta=\alpha^{-\frac{1}{\beta}}\right) \to\alpha^{1+\frac{1}{\beta}} \beta=1$$
$$\beta-1=\dfrac{1}{\beta} \to \beta=1+\dfrac{1}{\beta}$$
$$\alpha^{\beta} \beta=1$$
$$\alpha=\left(\dfrac{1}{\beta}\right)^{\frac{1}{\beta}}$$
$$\to \alpha=\left( \beta-1\right)^{\beta-1}$$
したがって、
$$ \begin{cases} \beta={\color{green} \phi}、\alpha=\left( {\color{green} \phi}-1\right)^{{\color{green} \phi}-1} \\ \beta={\color{green} \phi}-1、\alpha=\left( -{\color{green} \phi}\right)^{-\phi} \end{cases} $$
したがって、
$$f(x)=\alpha x^{\beta}$$
$$f(x) =\left( {\color{green} \phi}-1\right)^{{\color{green} \phi}-1} x^{{\color{green} \phi}}、f(x)=\left(-{\color{green} \phi}\right)^{-\phi} x^{1-{\color{green} \phi}}$$
もう一つ示してみましょう。
$$f(x)=({\color{green} \phi}-1)^{{\color{green} \phi}-1} x^{{\color{green} \phi}} \to f'(x)=(-1)^{{\color{green} \phi}-1} {\color{green} \phi} x^{{\color{green} \phi}-1}$$
$$f^{-1}(x)=\left( \dfrac{x}{({\color{green} \phi}-1)^{{\color{green} \phi}-1}}\right)^{\frac{1}{{\color{green} \phi}}}$$
$${\color{green} \phi}^2-{\color{green} \phi}-1=0 \to {\color{green} \phi}-1-\dfrac{1}{{\color{green} \phi}}=0$$
$$\to {\color{green} \phi}-1=\dfrac{1}{{\color{green} \phi}}$$
$$\to f'(x)=\left(\dfrac{1}{{\color{green} \phi}}\right)^{\frac{1}{{\color{green} \phi}}} {\color{green} \phi} x^{\frac{1}{{\color{green} \phi}}}={\color{green} \phi}^{1-\frac{1}{{\color{green} \phi}}} x^{\frac{1}{{\color{green} \phi}}}$$
$$\to f'(x)=\dfrac{x^{\frac{1}{{\color{green} \phi}}}}{({\color{green} {\color{green} \phi}}-1)^{({\color{green} \phi}-1) \frac{1}{{\color{green} \phi}}}}=\dfrac{1}{({\color{green} \phi}-1)^{1-\frac{1}{{\color{green} \phi}}}} x^{\frac{1}{{\color{green} \phi}}}$$
$$=\dfrac{1}{\dfrac{1}{{\color{green} \phi}^{1-\frac{1}{{\color{green} \phi}}}}} x^{\frac{1}{{\color{green} \phi}}}$$
$$\to f^{-1}(x)={\color{green} \phi}^{1-\frac{1}{{\color{green} \phi}}}x^{\frac{1}{{\color{green} \phi}}}=f'(x)$$
黄金比にまみれました。この結果は、非常に興味深い結果であると思います。
無理やり数値代入でも、ゴリゴリ計算したとしても、結果が黄金比で収束する(数学的な意味ではない)ことは非常に面白いことです。
なお、この問題は、この関数以外に解を持つかどうかが不明です。発見した方は、ご返信ください!
さて、徐々に面白みが出てきたところで、次の積分に行きます。
この積分は、また一風変わった形で数が出てきます。ぜひ一度チャレンジを!!!
$$\lim_{k \to \infty} \dfrac{\sqrt{k}}{e^k} e^{\int_{0}^{\infty} \lfloor{ke^{-x}} \rfloor dx} (k \in \mathbb{Z})$$
見た目ゴツイですが、超幾何級数よりはマシだと思うので、示しましょう。
なお、積分は、$e$の肩についています。(つまり累乗)
解答にどんな数が出てくるのか、予想してみてください。
俺はお前のことを忘れていた
$$I= \int_{0}^{\infty} \lfloor{ke^{-x}} \rfloor dx$$と置く。そして、$ke^{-x}=u$と置換。
$x=-\log \frac{u}{k}、dx=-\frac{1}{u} du$
$x=0\to u=k、x = \infty \to u=0$だから、
$$I=-\int_{k}^{0} \dfrac{\lfloor{u}\rfloor}{u} du$$
$$=\int_{0}^{k}\dfrac{\lfloor{u}\rfloor}{u} du $$
ここで、床関数の性質$n< u< n+1、\lfloor{u}\rfloor=n$から、
$$\int_{0}^{1}+\int_{1}^{2}+\int_{2}^{3} \cdots \int_{k-1}^{k} \dfrac{\lfloor{u}\rfloor}{u} du $$を考える。
ここで、床関数の性質から、
$$I=\int_{1}^{2} \dfrac{1}{u} du+\int_{2}^{3} \dfrac{2}{u} du+\cdots +\int_{k-1}^{k} \dfrac{k-1}{u} du$$
$$=\sum_{n=1}^{k-1} \int_{n}^{n+1} \dfrac{n}{u} du$$
$$=\sum_{n=1}^{k-1} \left.n \log u\right|_{n}^{n+1}$$
$$=\sum_{n=1}^{k-1} n\left( \log(n+1)-\log n\right)$$
これを総和記号$\sum$を用いずに表すと、$$I=\left( \log 2-\log1\right)+2\left( \log 3-\log 2\right)+3\left( \log 4-\log 3\right)+\cdots \left(k-1\right) \left( \log k-\log (k-1)\right)$$
$$=-\left( \log2+\log 3+\log 4+\cdots +(k-1)\right) +(k-1)\log k$$
$$=-\log {\left(1\cdot 2\cdot 3\cdots(k-1)\right)} +\log {k^{k-1}}$$
$$=-\log(k-1)!+\log {k^{k-1}}$$
$$\therefore I=\log {\dfrac{k^{k-1}}{(k-1)!}}$$
これを、元の極限の式に代入して、
$$\lim_{k \to \infty} \dfrac{\sqrt{k}}{e^k} e^{I}=\lim_{k \to \infty} \dfrac{\sqrt{k}}{e^k} \dfrac{k^{k-1}}{(k-1)!}$$
$$=\lim_{k \to \infty} \dfrac{\sqrt{k}}{e^k} \dfrac{k\cdot k^{k-1}}{k\cdot(k-1)!}$$
$$=\lim_{k \to \infty} \dfrac{\sqrt{k}}{e^k}\dfrac{k^k}{k!}$$
ここから後処理。
$Starling$の公式から、$k \to \infty、k! \sim \sqrt{2{\color{red} \pi} k}\left(\dfrac{k}{e}\right)^k$がいえるから、
$$\lim_{k \to \infty} \dfrac{\sqrt{k}}{e^k} \dfrac{k^k}{\sqrt{2{\color{red} \pi}} \sqrt{k}} \dfrac{e^k}{k^k} $$
$$\therefore \dfrac{1}{\sqrt{2{\color{red} \pi}}}$$
いかがでしたでしょうか。
階乗の近似公式に${\color{red} \pi}$が出てきていましたね。
そこまで難しくはないですが、$k!$にすることができたら楽でしたね。
次は、またちょっと違う積分です。
$$\int_{0}^{\infty} \int_{0}^{\infty} e^{-x} \left( \dfrac{x}{y}\right)^2 \log\left( 1+\dfrac{y^2}{x^2}\right) \log y dxdy$$
見た目がゴツイです。それに限ります。
重積分に関して、何かわからないことなどがありましたら、
こちら
をご覧ください。
この積分に、どのような数学定数が関係してくるのでしょうか。
一応自然対数があるので、$e$は絡んできそうですね。
是非予想してみてくださいな。
答えはきれい
積分を$I$とおく。
そして、この積分は、
$$I=\int_{0}^{\infty} \int_{0}^{\infty} e^{-x} \left( \dfrac{x}{y}\right)^2 \log\left( 1+\dfrac{y^2}{x^2}\right) \log y dydx$$
ここで、$ \frac{y}{x}=u\to dy=xdu$ だから、
$$\int_{0}^{\infty} \int_{0}^{\infty} e-{-x} \dfrac{1}{u^2} \log \left( 1+u^2\right) \log (xu) x dudx$$
ここで、$\log xu=\log x+\log u$
$$\int_{0}^{\infty} \int_{0}^{\infty} \dfrac{xe^{-x}}{u^2} \log(1+u^2) \log u dudx+\int_{0}^{\infty} \int_{0}^{\infty} \dfrac{xe^{-x}}{u^2} \log(1+u^2) \log x dudx$$
$$=\int_{0}^{\infty} xe^{-x} dx \int_{0}^{\infty} \dfrac{\log(1+u^2) \log u}{u^2} du+\int_{0}^{\infty} xe^{-x} \log x dx \int_{0}^{\infty} \dfrac{\log(1+u^2)}{u^2} du$$
それぞれの積分ごとに、$I_1、I_2、I_3、I_4$と置くと、$I=I_1I_2+I_3I_4$となる。
ここで、$I_2=I_4=\pi$だから、
あとは、$$I_1=\int_{0}^{\infty} xe^{-x} dx、I_3=\int_{0}^{\infty} xe^{-x} \log x dx$$を求める。
ここで、$$\Gamma(z)=\int_{0}^{\infty} x^{z-1} e^{-x} dx$$だから、
$I_1=\Gamma(2)=1$
$$I_3=\int_{0}^{\infty} xe^{-x} \log x dx $$
$$=\dfrac{\partial}{\partial z} x^{z-1} =x^{z-1} \log x$$
$$ここで、\dfrac{d}{dz} \Gamma(z)=\dfrac{d}{dz} \int_{0}^{\infty} x^{z-1} e^{-x}を考えると、$$
$$I_3=\int_{0}^{\infty} \dfrac{\partial}{\partial z} x^{z-1} e^{-x} dx$$
そして、$$\Gamma'(z)=\int_{0}^{\infty} x^{z-1} e^{-x} \log x dx$$
今回、$z-1=1 \to z=2$だから、$I_3=\Gamma'(2)$
そして、$$\Gamma'(1)=\int_{0}^{\infty} e^{-x} \log x dx=-\gamma $$
$\Gamma(z+1)=x\Gamma(x) \to \Gamma'(z+1)=x\Gamma'(x)=\Gamma'(2)=-{\color{orange} \gamma}+1$
以上より、$I=I_1I_2+I_3I_4$だから、
$I={\color{red} \pi}+(1-{\color{orange} \gamma}){\color{red} \pi}$
$\therefore I={\color{red} \pi}(2-{\color{orange} \gamma})$
いかがでしたでしょうか。
だいぶオイラー定数${\color{orange} \gamma}$が出てくるタイミングがわかってきました。
$$\int_{0}^{2{\color{red} \pi}} \dfrac{1}{\Gamma\left( 1-e^{ix}\right)} dx$$
ガンマ関数の中の虚数単位をどのように処理すべきかが難点そうですね。
答えはきれい
この積分には、多少の複素関数が絡みます。
まず、積分を$I$とおく。この時、
$$I=\int_{0}^{\frac{\pi}{2}} \dfrac{\Gamma(e^{ix})}{\Gamma(e^{ix}) \Gamma(1-e^{ix})} dx$$
ここで、$\Gamma(z) \Gamma(1-z)={\color{red} \pi} \csc {\color{red} \pi} z$から、
$$I=\int_{0}^{\frac{\pi}{2}} \dfrac{\Gamma(e^{ix})}{{\color{red} \pi} \csc ({\color{red} \pi} e^{ix})} dx$$
$$=\dfrac{1}{\pi}\int_{0}^{\frac{\pi}{2}} \Gamma(e^{ix}) \sin({\color{red} \pi} e^{ix})$$
ここで、$e^{ix}=z \to ie^{ix}=dz=iz \to dx=\frac{dz}{iz}$だから、
$$I=\dfrac{1}{\pi i} \int \dfrac{\Gamma(z) \sin({\color{red} \pi} z)}{z} dz$$
ここで、$e^{iz}=z$は、
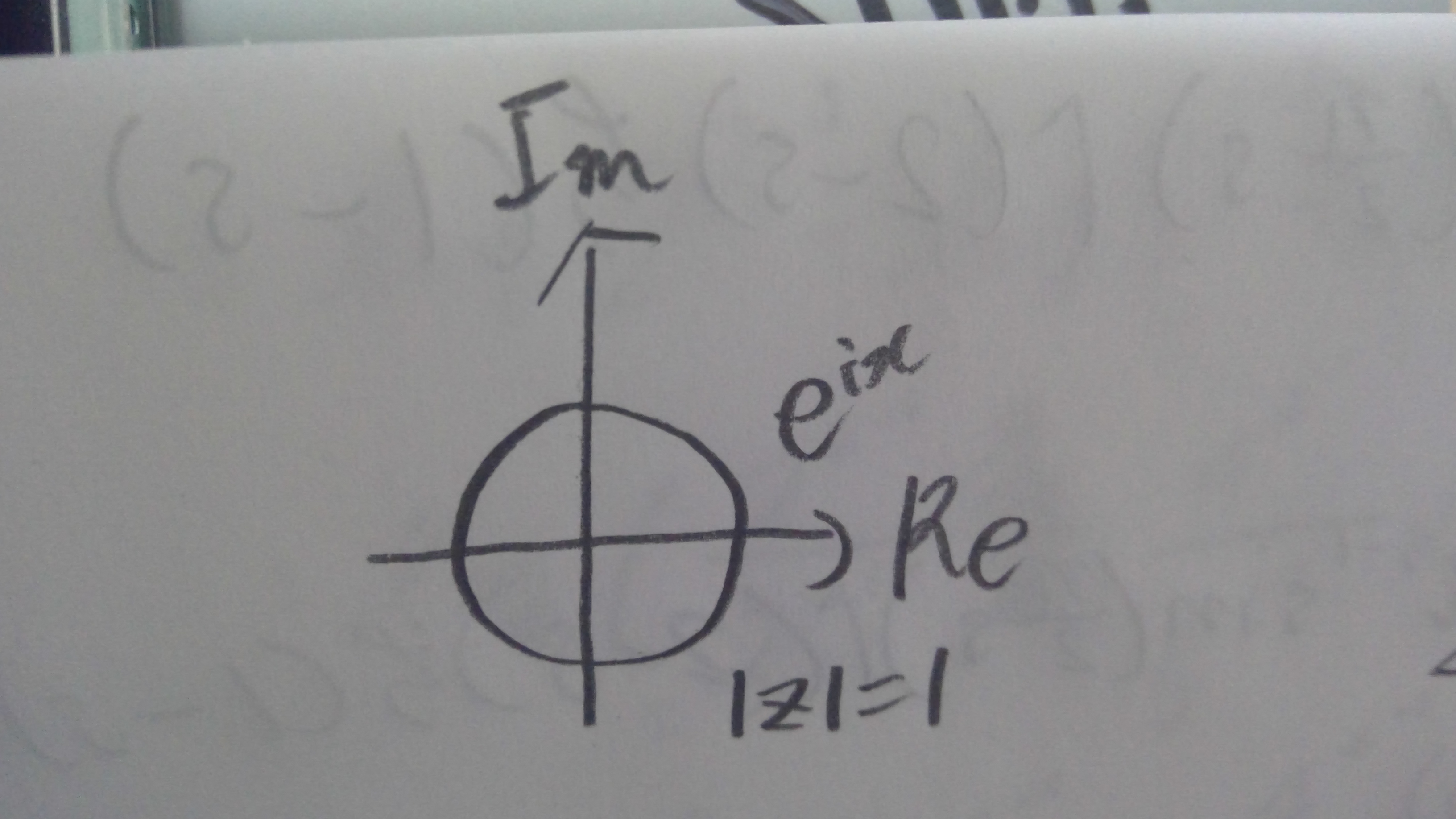図
上の図のようになるから、
$$I=\dfrac{1}{{\color{red} \pi} i} \oint_{|z|=1} \dfrac{\Gamma(z) \sin({\color{red} \pi} z)}{z} dz$$
$$I=\dfrac{1}{{\color{red} \pi} i} 2{\color{red} \pi} i \sum \mathbf{Res} \dfrac{\Gamma(z) \sin({\color{red} \pi} z)}{z} dz$$
$$I=2\mathbf{Res}_{z=0} \left(\dfrac{\Gamma(z) \sin({\color{red} \pi} z)}{z} \right)$$
$$=2\lim_{z \to 0} \dfrac{z \Gamma(z) \sin({\color{red} \pi} z)}{z}$$
$$=2\lim_{z \to 0} \Gamma(z+1) \dfrac{\sin {\color{red} \pi} z}{z}$$
$$\therefore I=2{\color{red} \pi}$$
次の積分です。
$$ \int_{-\infty}^{+\infty} e^{-x^2} \cos(2x^2) dx$$
評価されるべき
今回考慮すべきは、実部なので、実部を主に調べていく。
$Euler's formula$より、$$\cos(2x^2)=\Re \left( {\color{purple} e}^{i(2x)}\right)$$
$$I=\Re \int_{-\infty}^{\infty} {\color{purple} e}^{-x^2} {\color{purple} e}^{2ix} dx$$
$$=\Re \int_{-\infty}^{\infty} {\color{purple} e}^{-x^2(1-2i)} dx$$
$$=2\Re \int_{0}^{\infty} {\color{purple} e}^{-x^2(1-2i)} dx$$
ここで、$$I(t)=\int_{0}^{\infty} {\color{purple} e}^{-tx^2} (t \in \mathbb{C})$$を考える。
この時、ラプラス変換すると、
$$\mathcal{L}\left( I(t) \right) =\int_{0}^{\infty} {\color{purple} e}^{-st} I(t) dt$$
$$=\int_{0}^{\infty} {\color{purple} e}^{-st} \left( \int_{0}^{\infty} {\color{purple} e}^{-tx^2} dx\right) dt$$
$x$は独立であり、無理やるねじ込むと、
$$\mathcal{L} \left( I(t)\right) =\int_{0}^{\infty} \int_{0}^{\infty} {\color{purple} e}^{-st} {\color{purple} e}^{-tx^2} dxdt$$
有界性があるため、フビニの定理を用いて、
$$=\int_{0}^{\infty} \int_{0}^{\infty} {\color{purple} e}^{-st} {\color{purple} e}^{-tx^2} dtdx$$
$$\mathcal{L} \left( I(t)\right) =\int_{0}^{\infty} \left( \int_0^{\infty} {\color{purple} e}^{-st} {\color{purple} e}^{-tx^2} dt \right) dx$$
上の式において、()中は、$\mathcal{L} \left( {\color{purple} e}^{-tx^2}\right)$だから、
$$\mathcal{L} \left( I(t)\right) =\int_{0}^{\infty} \mathcal{L} \left( {\color{purple} e}^{-tx^2}\right) dx$$
$$=\int_{0}^{\infty} \dfrac{dx}{s+x^2}=\left.\dfrac{1}{\sqrt{s}} \arctan \dfrac{x}{\sqrt{s}}\right|_{0}^{\infty}$$
したがって、$$\mathcal{L} \left( I(t)\right) =\dfrac{1}{\sqrt{s}} \dfrac{\pi}{2} $$となる。
ここで、元に戻すために、逆ラプラス変換をすると、
$$\mathcal{L}^{-1} \mathcal{L}\left( I(t)\right)(s)=\mathcal{L}^{-1} \left(\dfrac{1}{\sqrt{s}} \dfrac{\pi}{2} \right) $$
この$\pi$を、$\sqrt{\pi} \sqrt{\pi}$ととらえると、
$$=\dfrac{\pi}{2} \mathcal{L}^{-1} \left( \dfrac{\sqrt{\pi}}{\sqrt{s}}\right) $$
$$=\dfrac{\pi}{2} \mathcal{L}^{-1} \left( \dfrac{\Gamma\left(\frac{1}{2} \right)}{\sqrt{s}}\right)$$
$$\dfrac{\pi}{2} \mathcal{L}^{-1} \left( \frac{\Gamma\left(-\frac{1}{2}+1 \right)}{s^{-\frac{1}{2} +1}}\right)$$
以上より、$$I(t)=\dfrac{\pi}{2} t^{-\frac{1}{2}}$$
となる。さて、求める積分に戻ると、
$$I=2\Re \int_{0}^{\infty} {\color{purple} e}^{-x^2(1-2i)} dx$$
$$I(1-2i)=\dfrac{\sqrt{\pi}}{2}(1-2i)^{-\frac{1}{2}}$$
ここで、$Z=1-2i \to |Z|=e^{i\alpha}$と置くと、
$|Z|=\sqrt{1^2+2^2}=\sqrt{5} と\alpha$
$$I(1-2i) =\dfrac{\pi}{2} (\sqrt{5}) ^{-\frac{1}{2}} {\color{purple} e}^{-\frac{i\alpha}{2}}$$
$$(\sqrt{5}) ^{-\frac{1}{2}}=\sqrt{\sqrt{5}} などから、$$
$$2\Re I(1-2i) =2\Re \left(\dfrac{\pi}{2} \dfrac{1}{\sqrt{\sqrt{5}}}{\color{purple} e}^{-\frac{i\alpha}{2}}\right)$$と置くと、$$I=\dfrac{\sqrt{\pi}}{\sqrt{\sqrt{5}}} \cos \dfrac{\alpha}{2}$$となるから、あとは、$\alpha$の値を求める。
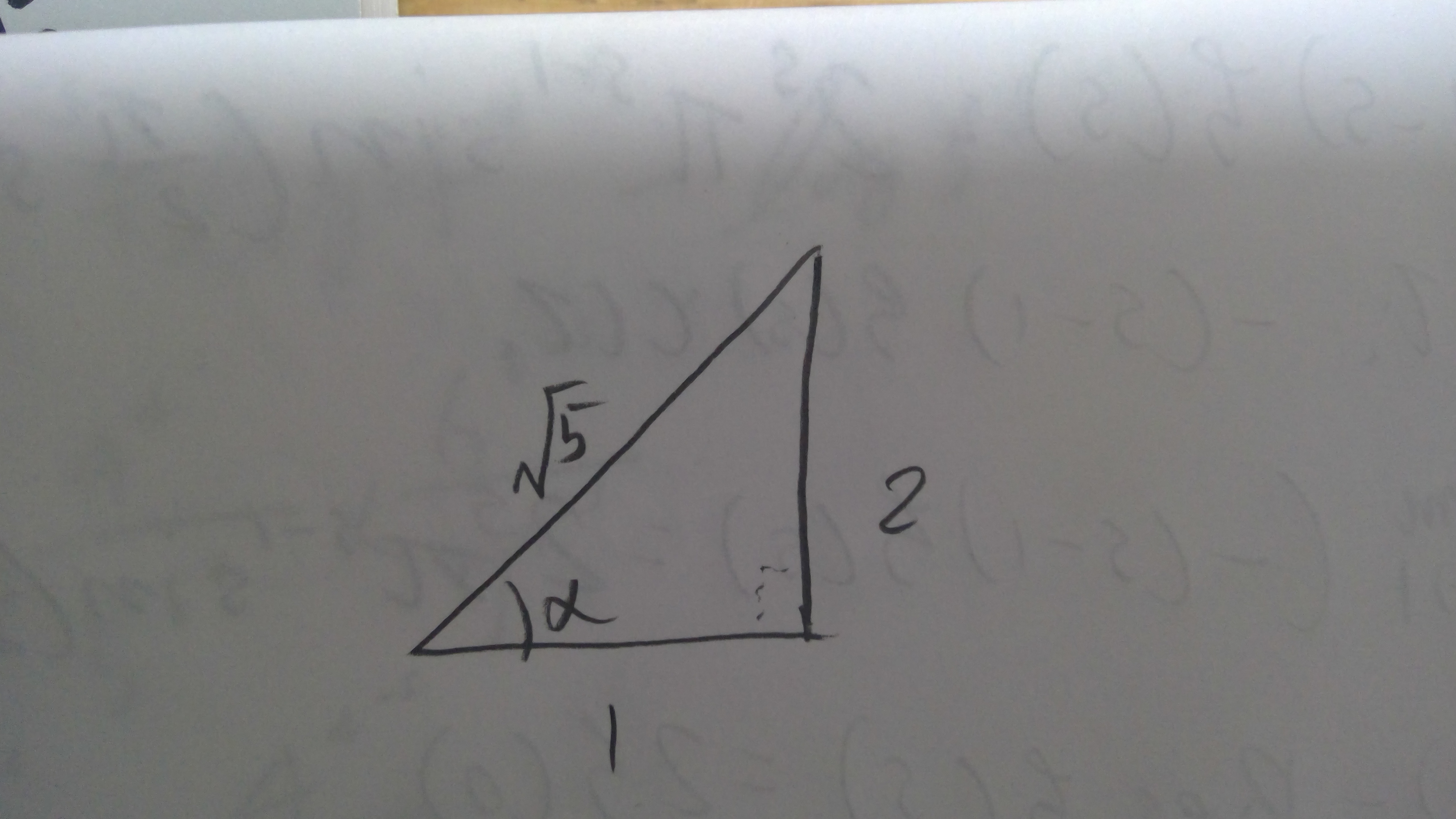図
上の図は、底辺が$1$の実数部を表す直角三角形
図の場所に$\alpha$をとると、垂線になるから、$Z$は、その長さを表す。(図参照)
したがって、$ \cos \alpha=\sqrt{\sqrt{5}}$ だから、半角の公式より、
$$\cos \dfrac{\alpha}{2} =\sqrt{\dfrac{1+\cos \alpha}{2}} \to \cos \dfrac{\alpha}{2}=\sqrt{\dfrac{1+\left( \sqrt{\sqrt{5}}\right)}{2}} \to \sqrt{\dfrac{1+\left( \sqrt{\sqrt{5}}\right)\cdot \sqrt{5}}{2\sqrt{5}}}=\sqrt{\dfrac{\phi}{\sqrt{5}}}$$
以上より、$\cos \dfrac{\alpha}{2}=\sqrt{\dfrac{{\color{green} \phi}}{\sqrt{5}}} $となるから、
$$I=\dfrac{\sqrt{\pi}}{\sqrt{\sqrt{5}}} \dfrac{\sqrt{{\color{green} \phi}}}{\sqrt{\sqrt{5}}}$$
$$\therefore I=\sqrt{\dfrac{{\pi {\color{green} \phi}}}{5}}$$
さて、いかがでしたでしょうか。この積分は、もっと評価されるべきだと思うのは、自分だけでしょうか???
この積分を乗せた理由としては、最後に黄金比が登場するところです。
多少の無理やり感は否めないですが。
しかしながら、このような形で、黄金比が登場するとは思いませんでした。
$$\sum_{n≧2} \dfrac{\zeta(n)-1}{n}$$
特殊関数登場
まずは解きましょう。
この級数を$S$とおく。
$$\sum_{n≧2} \dfrac{\left( \zeta(n)-1\right) \left( n-1\right)!}{n\left(n-1\right)!}$$
$$=\sum_{n≧2} \dfrac{\zeta(n) \Gamma(n)-\Gamma(n)}{n!}$$
$$=\sum_{n≧2} \dfrac{1}{n!} \left( \zeta(n)\Gamma(n)-\Gamma(n)\right)$$
ここで、$\Gamma(n)=\int_{0}^{\infty} {\color{purple} e}^{-x} x^{n-1} dx$だから、$$\to\int_{0}^{\infty} \dfrac{x^{n-1}}{{\color{purple} e}^x-1}=\zeta(n) \Gamma(n)$$
であるから、
$$=\sum_{n≧2} \dfrac{1}{n!} \left(\int_{0}^{\infty} \dfrac{x^{n-1}}{{\color{purple} e}^x-1}- \int_{0}^{\infty} {\color{purple} e}^{-x} x^{n-1} dx\right)$$
$$=\sum_{n≧2}\dfrac{1}{n!} \left( \int_0^{\infty} \left( \dfrac{1}{{\color{purple} e}^x-1} - \dfrac{1}{{\color{purple} e}^x}\right) dx\right)$$
$$=\sum_{n≧2} \int_0^{\infty} \dfrac{x^{n-1}}{n!} \left( \dfrac{1}{{\color{purple} e}^x-1} - \dfrac{1}{{\color{purple} e}^x}\right) dx$$
$$\therefore S=\int_0^{\infty} \left( \dfrac{1}{{\color{purple} e}^x-1} - \dfrac{1}{{\color{purple} e}^x}\right) \sum_{n≧2} \dfrac{x^{n-1}}{n!} dx$$
ここで、
$$\sum_{n≧2} \dfrac{x^n-1}{n!}=\dfrac{1}{x} \sum_{n≧2} \dfrac{x^n}{n!}$$
$$\dfrac{1}{x} \left( \sum_{n≧0} \dfrac{x^n}{n}-1-x\right)$$
ここで、${\color{purple} e}^x$のマクローリン展開から、$$\dfrac{1}{x} \left( {\color{purple} e}^x-1-x\right)$$
$$=\sum_{n≧2} \dfrac{x^{n-1}}{n!} =\dfrac{e^x}{x}-\dfrac{1+x}{x}$$
$$S=\int_0^{\infty} \left( \dfrac{1}{{\color{purple} e}^x-1} -\dfrac{1}{{\color{purple} e}^x}\right) \sum_{n≧2} \dfrac{x^{n-1}}{n!} dx$$
$$\int_0^{\infty} \left( \dfrac{1}{{\color{purple} e}^x-1} -\dfrac{1}{e^x}\right)\left( \dfrac{e^x}{x}-\dfrac{1+x}{x}\right)$$
$$\int_0^{\infty} \dfrac{e^x}{x\left( e^x-1\right))}-\dfrac{1+x}{x\left(e^x-1 \right)}-\dfrac{1}{x}+\dfrac{1+x}{xe^x} dx$$
$$\int_0^{\infty} \dfrac{e^x-1}{x\left( e^x-1\right))}-\dfrac{x}{x\left(e^x-1 \right)}-\dfrac{1}{x}+\dfrac{1+x}{xe^x} dx $$
だから、いろいろ消去して、
$$\int_0^{\infty} -\dfrac{1}{\left( e^x-1\right)} +\dfrac{e^{-x}} {x} +\dfrac{1}{e^x} dx$$
$$\int_0^{\infty} \dfrac{e^{-x}}{x} -\dfrac{1}{e^x-1}dx+\int_{0}^{\infty} e^{-x} dx$$
ここで、$$\psi(z)=\int_{0}^{\infty} \dfrac{e^{-x}}{x}-\dfrac{e^{-zx}}{1-e^{-x}} dx$$を用いると、
$$S=\left. \psi(1)-e^x\right|_{0}^{\infty}$$
$$\therefore S=1-{\color{orange} \gamma} \left( \because \psi(1)=-{\color{orange} \gamma}\right)$$
いかがでしたでしょうか。この級数の最後に、オイラー定数が出てくるなんて予想もできません。
この級数からは、何となくですが、リーマンゼータ関数とオイラー定数の関係がありそうな感じがしますね。
結局のところは、ガンマ関数までもっていってしまい、結果、微分して、ディガンマ関数になったところで、ある程度「オイラー定数が出てきそうだな」ということは予測できるのかもしれません。
物理と精通する数
さて,上では、数学に関していろいろと語りまくってきましたが、そろそろ分野を移行して「物理」に行きたいと思います。
物理には、基本的に、 $\color{purple} e、\color{magenta} i$の二種類が主に活躍します。
まず、$\color{purple} e$に関して
ネイピア数は、空気抵抗を加味した自由落下の数式に出てきます。
$$u=\dfrac{mg}{k} \left( 1-{\color{purple} e}^{\frac{kt}{m}}\right)$$
変数分離形の微分方程式
$$m \dfrac{dv}{dt}=mg-kv$$を満たす関数を求めればよい。
ただし、初期条件は、$t=0、v=0$
両辺を$mg-kv$で割ると、
$$\dfrac{m}{mg-kv} \dfrac{dv}{dt}=1$$
両辺を$t$で積分して、
$$\int \dfrac{m dv}{mg-kv}=\int t dt$$
あとは、この積分を計算し、上の式を得る。
勿論、$$v=\dfrac{mg}{k}$$も解である。
なお、こちらの数式は、 https://manabitimes.jp/math/1013 を参考にした
$i$に関して
$$ i \hbar \dfrac{\partial}{\partial t} \psi(r,t) = \left(- \dfrac{\hbar^2}{2m} \nabla^2+ V(r,t) \right) \psi(r,t) $$
シュレーディンガー方程式（シュレーディンガーほうていしき、英: Schrödinger equation）とは、物理学の量子力学における基礎方程式である。 シュレーディンガー方程式という名前は、提案者であるオーストリアの物理学者エルヴィン・シュレーディンガーにちなむ。1926年にシュレーディンガーは量子力学の基礎理論に関する一連の論文を提出した。
シュレーディンガー方程式の解は一般的に波動関数と呼ばれる。波動関数はまた状態関数とも呼ばれ、量子系（電子など量子力学で取り扱う対象）の状態を表す。シュレーディンガー方程式は、ある状況の下で量子系が取り得る量子状態を決定し、また系の量子状態が時間的に変化していくかを記述する。あるいは、波動関数を量子系の状態を表すベクトルの成分と見た場合、シュレーディンガー方程式は状態ベクトルの時間発展方程式に置き換えられる。状態ベクトルによる記述は波動関数を用いた場合と異なり物理量の表現によらないため、より一般的である。シュレーディンガー方程式では、波動関数や状態ベクトルによって表される量子系の状態が時間とともに変化するという見方をする。状態が時間変化するという考え方はシュレーディンガー描像と呼ばれる。(Wikipedia)
シュレディンガー方程式(表記ブレはご容赦を)は、簡単に説明いたしますと、「波(エネルギー)」と、「力」を結びつける方程式です。
一番最初の虚数単位$i$は、本当にわかりやすく説明するのであれば、微分した結果前に出てきてしまったものだという認識です。
(恩師に感謝)
化学と精通する数
化学には、「アレニウスの式」というものが存在します。
$$ k = A \exp \left( - \dfrac{E_a}{RT} \right) $$
ここの章は、
https://astro-dic.jp/boltzmann-distribution/
こちらを参考にしている。
この式について詳しく見ていきます。(ボルツマンという名前が出てきます。)
このアレニウスの式というのは、スウェーデンの化学者である、アレニウスが提唱した式です。
化学反応が生じる条件は、「原子や分子が衝突したときに活性化エネルギー以上のエネルギーを獲得していること」です。アレニウスの式は、衝突回数と活性化エネルギー以上のエネルギーを獲得する確率の積であり、これは化学反応が生じる確率に一致します。
アレニウスの式も、後半(exp)の部分は、確率と絡みます
この式の変数は、
$k=反応速度定数 R=気体定数 E=活性化エネルギー$
$A=度数因子(独立している)、T=温度$を表しています。
しかし、この式になぜ$e$が登場するのでしょうか。
それを見ていきます。
反応速度定数と活性化エネルギーについて
アレニウスの式を語るうえで、避けて通れないのがこの「活性化エネルギー」です。
まず、反応速度定数に関してですが、一つ例を挙げてみます。
$A、B$という物質から、$C、D$という物質に変化する化学反応を見てみます。
$aA+bB\to cC+dD (a、b、c、dは係数)$となりますが、この時の反応速度は、$v=k[A]^{m}[B]^{n} (ただし、[A]、[B]は、A、Bの濃度を表す)$によって書けることが一般的に知られています。この式の比例定数$k$のことを、アレニウスの式の左辺でもある、「反応速度係数」といいます。つまり、この反応速度係数を求めるための式がアレニウスの式といえますね。
また、この式から自明ですが、反応速度係数$k$の値が大きければ大きいほど反応速度$v$は早くなり、逆に反応速度係数$k$が小さければ、反応速度$v$も小さくなります。
反応速度係数$k$の単位は、反応速度$v$の単位によって異なります。
また、反応速度係数$k$の値は、同一温度条件では、各々の反応において固有な値をとります。しかしながら、温度条件が変化すると、反応速度係数$k$の値も変化します。
化学反応が起こるとき、それぞれの物質が持つエネルギー(ポテンシャルエネルギー)の収支のみでは、説明することができない余分なエネルギーが関与します。このエネルギーのことを、「活性化エネルギー」といいます。
分子や原子などがお互いに衝突し、結合反応などの反応が生じる時、この活性化エネルギーを考慮しなければならなくなることが多いです。
さて、ここまで長々と説明してきましたが、アレニウスの式になぜ$e$が出てくるのか。
その理由は、$e$だけでなく、$\exp \left( - \dfrac{E_a}{RT} \right) $に関係があります。
この部分は、「ボルツマン因子」と呼ばれる部分です。
ボルツマン因子は、簡単に説明いたしますと、「温度が一定で、熱平衡にあり、体積の変化や、粒子の出入りがないときに、ある状態が発現する相対的な確率を表すもの」であります。
先ほど、アレニウスの式の説明の部分でも「確率」という言葉が出てきましたが、その言葉は、この「ボルツマン因子」からきているのですね。
ボルツマン因子が出てきました。最後に、ボルツマン因子に関係のある「ボルツマン定数」に関して説明します。
ボルツマン定数は、「気体定数をアボガドロ定数で割った値」であります。
さて、このボルツマン定数が用いられる統計学的な分野に、「ボルツマン分布」があります。
ボルツマン分布とは、「熱平衡にある、古典的な粒子に関する確率統計」です。
簡単に説明すると、
エネルギーが$E_{i}$の状態にある分子の数が$\exp \left(\frac{-E_i}{K_{B} T}\right)$に比例する
ということを表しています。
この分布に関して、量子性を鑑みると、フェルミ統計やボース統計になる。
ここまでボルツマン分布に関して説明してきましたが、「フェルミ統計」などの、多少関係のあるものについて、軽く齧ります。
フェルミ統計とは、電子や中性子、ニュートリノなどフェルミ粒子の集団が従う統計規則。フェルミ分布あるいはフェルミ-ディラック分布ということもある。同一種類の複数のフェルミ粒子は区別がつかない。またパウリの排他原理により、同じ状態に複数の粒子は存在できない。このために温度$T$で熱平衡にある場合、状態$i$の分布関数は、
$$f=\dfrac{1}{\exp\left[ \dfrac{\epsilon_{i}-\mu}{K_{B} T}\right]-1}$$
と表される。ここで$\epsilon_{i}$は状態、$i$ のエネルギー準位、$\mu$は化学ポテンシャル、$K_{B}$はボルツマン定数である。化学ポテンシャル$\mu$が負の大きな数の場合、ボルツマン分布に近づく。化学ポテンシャルが基底状態のエネルギーより高く、温度が低い場合、縮退圧を発生させるようなフェルミ縮退という状態が実現する。
ボース統計に関して
光子やアルファ粒子などボース粒子の集団が従う統計規則。ボース-アインシュタイン統計あるいはボーズ分布ということもある。同一種類の複数のボース粒子は区別がつかず、また何個でも同時に同じ状態に存在できる。このために温度$T$ で熱平衡にある場合、状態$i$の分布関数は、
$$f=\dfrac{1}{\exp\left[ \dfrac{\epsilon_{i}-\mu}{K_{B} T}\right]-1}$$
と表される。ここで$\epsilon_{i}$は状態、$i$ のエネルギー準位、$\mu$は化学ポテンシャル、$K_{B}$はボルツマン定数である。化学ポテンシャル$\mu$が負の大きな数の場合、ボルツマン分布に近づく。
化学ポテンシャルはつねに基底状態のエネルギーより低い。基底状態のエネルギーと等しくなるとボース-アインシュタイン凝縮を起こす。フェルミ統計も参照。
分布
(上の画像は、
https://astro-dic.jp/bose-statistics/
にあったもの)
このように、一見数学とは(専門的に)関係のない分野においても、$e$などの定数が活躍します。
あとがき
さて、ここまで様々な観点(主に積分)で数学定数に関してみてきました。
お互いにものすごく深い関係があるのにも関わらず、オイラーの等式やネイピア数、円周率などが多く出てきてしまっているのが今の数学の現状です。
なんか寂しいですね。
最後に。
蛇足
$$\eta(s)=\sum_{k≧1} \dfrac{(-1)^{k-1}}{k^s}$$
$$=\dfrac{1}{1^s}-\dfrac{1}{2^s}+\dfrac{1}{3^s}+\dfrac{1}{4^s}+\cdots$$
$$\to ^eta(s)=1^{-s}-2^{-s}+3^{-s}-4^{-s}+\cdots$$
ここで、$\frac{d}{ds} \eta(s)$を考える。
$$\to \eta'(s)=-1^{-s} \log 1+2^{-s} \log 2-3^{-s} \log 3+4^{-s} \log 4 -\cdots$$
$$=\log 2^{2^{-s}}-\log 3^{3^{-s}}+\log 4^{4^{-s}}-\log 5^{5^{-s}} \cdots$$
$$=-\log \left( \dfrac{2^{2^{-s}}}{3^{3^{-a}}} \cdot \dfrac{4^{4^{-s}}}{5^{5^{-s}}} \cdot \dfrac{6^{6^{-s}}}{7^{7^{-s}}}\right)$$
$$\to {\color{purple} e}^{\eta'(s)}=\left( \dfrac{2^{2^{-s}}}{3^{3^{-a}}} \cdot \dfrac{4^{4^{-s}}}{5^{5^{-s}}} \cdot \dfrac{6^{6^{-s}}}{7^{7^{-s}}}\right)$$
$s=0$の時、
$${\color{purple} e}^{\eta'(s)}=\dfrac{2\cdot 4\cdot 6\cdots}{3\cdot 5\cdot 7\cdots}$$
$$\left({\color{purple} e}^{\eta'(s)}\right)^2=\left(\dfrac{2\cdot 4\cdot 6\cdots}{3\cdot 5\cdot 7\cdots}\right)^2$$
$$\to {\color{purple} e}^{2\eta'(0)}=\dfrac{\pi}{2}$$
$$\to 2\eta'(0)=\log \dfrac{\pi}{2}$$
$$\to \eta'(0)=\dfrac{1}{2}\log \dfrac{\pi}{2}$$
ゼータ関数に関して
$$\eta(s)=\left( 1-2^{1-s}\right) \zeta(s)$$
$\frac{d}{ds} \eta(s)$を考える。
$$\eta'(s)=\left( 1- 2^{1-s}\right) \zeta'(s) +\left( 2^{1-s} \log 2\right) \zeta(s)$$
$s=0$の時、
$$\eta'(0)=-\zeta'(0)+\left( 2\log 2\right) \zeta(0)$$
$$\zeta(s)=2^s \pi^{s-1} \sin \left( \dfrac{\pi}{2} s\right) \Gamma(1-s) \zeta(1-s)$$
ここで、$(1-s) \zeta(s)$を考えると、
$$(1-s) \zeta(s) =2^s \pi^{s-1} \sin \left(\dfrac{\pi}{2} s \right)\Gamma(2-s) \zeta(1-s)$$
ここで、$-(s-1) \zeta(n)$として、
$$\lim_{s \to 1} \left( -(s-1) \zeta(s) 2^s \pi^{s-1} \sin \left(\dfrac{\pi}{2} s \right)\Gamma(2-s) \zeta(1-s)\right)$$
$$\to \mathrm{Res}_{s=1} \zeta(s) =2\zeta(0)$$
$$\zeta(s)=\dfrac{1}{s-1}+\gamma+O(s-1)$$
$$\to (s-1) \zeta(s)=1+\gamma+(s-1)O(s-1)$$
$$\lim_{s \to 1} (s-1) \zeta(s)=\mathrm{Res}_{s=1} \zeta(s)=1$$
$$\to \eta'(0)= -\zeta'(0) +(2\log 2)\zeta(0)$$
$$\to \dfrac{1}{2} \log \dfrac{\pi}{2}=-\zeta'(0) +(2 \log 2)\left( -\dfrac{1}{2}\right)$$
$$\zeta'(0)=-\log 2-\log \sqrt{\dfrac{\pi}{2}}$$
$$=-\left( \log \left( \sqrt{\dfrac{\pi}{2}} \cdot 2\right)\right)$$
$$=-\left( \log \sqrt{2\pi}\right)$$
$$\therefore \zeta'(0)=\log \dfrac{1}{\sqrt{2\pi}}$$
未解決問題
有名なものは、$\pi-{\color{purple} e}$の無理数性の証明です。
数$Ⅰ$の集合の分野で命題の問題で、必ずといっていいほど出てくる、「有理数+有理数=有理数」的なものの延長線上です。
これ以外はあまり耳にしませんが、先ほど挙げたとおり、$\color{orange} \gamma $の無理数or有理数の評価なども未解決問題です。
クリスマスまでの記事リレー的なmathlog様の公式イベントの「大学数学基礎」のほうで投稿いたしましたが、他投稿者様のレベルが高く、合わせる顔がありません。
しかしながら、「特殊な知識がなくても理解できる」ことを意識して書いたので、悪しからず。
オイラー定数に関して、自分はあまり今まで向き合ったことがないことが現状でした。しかしながら、特殊関数などを調べていくうちに、徐々にオイラー定数が出てくる機会が増加していき、「あ、これほかの数(円周率や自然対数の底)と関係あるじゃん」などと思うことが多くなり、この記事を書いた次第です。
ディガンマ関数を用いること以外にも、オイラー定数の定義の仕方があります。これも非常に興味深いです。
好評であれば特殊関数版や続編も出そうと思います。
$$ 完 $$
何か気になることなどがございましたら、何なりと返信ください。。
なお、議論不十分な箇所がいくらか存在すると思います(作者承知)。
色はあまり意味はありません。
MEMO
複素対数関数のミスを修正いたしました。(2023年12月22日)