はじめての圏論 ― ① 何のための圏論？

新興宗教「圏論」

ここ５０年くらいで圏論への風当たりは一転し、今ではブームと言っていいほど人気が無駄に高い。だが、相変わらずよく避けられている。傍から見れば「ヘンテコな矢印だけの謎語」で全ての数学をしようとする過激派^*1が湧きだしたあたりから、「一度踏み出せば後戻りができなくなる宗教」という揶揄も目に入るようになった。どうやら今でもその残党は身を潜めているようだ（最近失踪した自称数学者Youtuberがわざわざ動画を作ってまでした忌避アピールを見たときは、粘度が変なバグり方したツンデレかと思った。それとも数学に嫌われすぎて老けたのか？）。

この記事では、圏を考えるモチベ的な偏見をなんとなーく話す。圏論初めての人向けの記事である。少なくとも耄碌の戯言に煽られる人を減らすくらいはできるだろう。宗教圏論に入信しなくても圏論はできることを知ってもらいたい。

本文

まず圏とは何か？

圏とは有向グラフに髭が付いたものである。有向グラフとは、点と、それらの間に伸びる矢印のネットワークを表す代数的構造を言う。まずはこれを定義しよう。

$V$は点全体の集まり、$E$は矢印全体の集まり、$\text{dom}:E\rightarrow V;$は矢印に始点を割り当てる写像、$\text{cod}:E\rightarrow V$は矢印に終点を割り当てる写像と呼ぶ。この定義から、点と矢印のネットワークを表現できることが分かるだろうか？どの矢印も１つの点から１つの点に向かって伸びている。

２点$x,y\in V$に対して、$\text{Hom}(x,y)\coloneqq\{f\in E\mid\text{dom}(f)=x,\text{cod}(f)=y\}$、$\text{End}(x)\coloneqq\text{Hom}(x,x)$と定義する。$\text{Hom}(x,y)$は$x$から$y$に伸びる矢印全体の集合と読む。

集合だけ与えられてもただの物の集まりがあるだけだが、そこに演算を入れれば追加情報を与えられる。例えば集合$G$に二項演算$+$を入れてアーベル群$(G,+)$とすれば、$G$の要素を使って算数ができる。こういうのを代数的構造という。有向グラフもその一種だが、考える集合は$V$と$E$の２つだ。アーベル群に構造を保つ写像(＝準同型)があるように、台集合が２個の場合も構造を保つ写像が定義できる。

それでは、圏を定義する。圏とは、有向グラフに$\text{id}$（アイデンティティ）という特別な矢印と、矢印の合成という関係と、これらが満たす公理を付けたものである。

圏の場合、点のことを「対象」、矢印のことを「射」と呼ぶ。$\text{cod}(f)=\text{dom}(g)$が成り立つことを「$(g,f)$は合成可能である」という。先ほどと同様、各$x,y\in\mathcal{C}$に対して$\text{Hom}_\mathcal{C}(x,y)\coloneqq\{f\in\text{Mor}_\mathcal{C}\mid\text{dom}(f)=x,\text{cod}(f)=y\}$、$\text{End}_\mathcal{C}(x)\coloneqq\text{Hom}_\mathcal{C}(x,x)$と定義する。全ての$x,y\in\mathcal{C}$に対して$\text{Hom}_\mathcal{C}(x,y)$が集合のとき、圏$\mathbfcal{C}$は局所小圏であるという。対象全体$\mathcal{C}$及び射全体$\text{Mor}_\mathcal{C}$が集合のとき、圏$\mathbfcal{C}$は小圏であるという。

圏の準同型を関手かんしゅという。

定義より、関手の射のほうの写像$F$は、各$x,y\in\mathcal{C}$に対して$f\in\text{Hom}_\mathcal{C}(x,y)$なる射$f$を$\hspace{-1.5pt})F$$\hspace{-2.3pt}f)\in\text{Hom}_\mathcal{D}(F(x),F(y))$に移すことが分かる。

同型類を分類するための圏論

このように、圏自体は群や位相空間、半順序集合のような数学的構造の一種に過ぎない。圏の真価は、対象を群やベクトル空間などの数学的構造の集まりとしたときに発揮される。圏を成す数学的構造は、射だけでその性質を完全に表現できる。このことを簡単に話す。

まず、対象が数学的構造、射が構造を保つ写像（＝準同型写像）が成す圏の例を挙げる。

私たちが近代から慣れ親しんできたほとんど^*3全ての数学的構造は、構造を保つ写像と共に圏を成す。近代以降、私たちは集合に何か構造を入れることで色々な概念を定義し、構造を保つ写像を駆使して構造の多様性を記述してきた。これを簡素化すれば、ただの点と矢印だけのネットワークになるのは当たり前だ。では、逆にそれだけでどこまで記述できるのだろう？というのが具体圏論というもの。そしてその答えは……冒頭で述べた通り原理上は全てが記述できる。

同型と性質

数学的構造には、「構造として同じ」という意味の同型という同値関係が伴う。同型のとき変わらない量（＝同型不変量）のことを性質という。例えば群$G_1,G_2$が同型$G_1\cong G_2$だったとしよう。台集合の濃度は群論的性質だ。$G_1\cong G_2$ならば$|G_1|=|G_2|$になる。二乗して１になる元の総数は群論的性質だ。$G_1\cong G_2$ならば$|\{g\in G_1\mid g^2 =1_{G_1}\}|=|\{g\in G_2\mid g^2 =1_{G_2}\}|$になる。群が可解群
かけいぐん（かけいぐん）かどうかは群論的性質だ。Yesを$1$、Noを$0$と見なせば、不変量として扱える。
さて、群全体の集まりを用意して、同型類を分類する状況を考えてみよう。同型類が完全に分類できれば、私たちは群について全てわかったことになる。すべての群は「台集合の濃度」や「二乗して１になる元の総数」といったパラメータを持っている。まず「台集合の濃度」に注目しよう。群全体の集まりの中で、台集合の濃度が１のもの、２のもの、３のもの、４のもの、……というように部屋分けすれば、別々の部屋にいる群同士は同型にならない。台集合の濃度は群論的性質だからだ。定義の対偶を取ると「$|G_1|\neq|G_2|$ならば$G_1\ncong G_2$」になることから言える。さて、これで完全に分類できただろうか？というとできてない。例えば台集合の濃度が４のものの中にも、互いに同型にならない群が混ざっている。では、さらに別のパラメータに注目して部屋分けして……を繰り返していけば、より正確な同型類に近づいていく。…いつか終わるのだろうか？

２つの群について、これとこれとこれとこの性質が同じならば同型になる！という性質たちを完全な性質（or 完全同型不変量）という。同型類を完全に分類できる性質たちと言ってもよい。例えば、ベクトル空間の次元は完全なベクトル空間論的性質である。$V_1\cong V_2\Leftrightarrow \dim(V_1)=\dim(V_2)$だからだ。

対象が数学的構造の圏について、射をいい感じに選ぶと、考えたい「同型$\cong$」と同型射の存在という圏の同値関係「$\cong_\mathcal{C}$」がちょうど一致することがある（名前からお察しの通り）。一度圏を成してしまえば、そこから$\text{Hom}$関手という完全な性質が自然に得られる。原理上は、圏の言葉だけで何もかもが書けてしまうのだ。これが圏を考える最大のメリットだろう。

長いので、以後は対象のほうの写像$\text{Hom}_\mathcal{C}(a,\cdot)$だけを書いて$\text{Hom}$関手を指すものとする。

定理１の自然同型は、以下の図式が可換になることを言っている。
\begin{xy} \xymatrix { \text{Hom}_\mathcal{C}(a,x) \ar[d]_{ f\circ_\mathcal{C}-} \ar@{->}[r]|{\cong_\textsf{Set}}^{\theta_x}& \text{Hom}_\mathcal{C}(b,x) \ar[d]^{f\circ_\mathcal{C}-} \\ \text{Hom}_\mathcal{C}(a,y) \ar@{->}[r]|{\cong_\textsf{Set}}^{\theta_y} & \text{Hom}_\mathcal{C}(b,y) \ar@{}[lu]|{\circlearrowright} } \end{xy}
これは一体どういうことか？まず、各$x\in\mathcal{C}$に対して$\text{Hom}_\mathcal{C}(a,x)\overset{\theta_x}{\cong}_\textsf{Set}\text{Hom}_\mathcal{C}(b,x)$となる全単射$\theta_x$の存在を言っている。これは$a$から$x$への射と$b$から$x$への射の本数が同じになるという意味だ。つまり$|\text{Hom}_\mathcal{C}(a,x)|=|\text{Hom}_\mathcal{C}(b,x)|$という意味だ。自分から伸びる射の本数は「性質」であるということだ。これをさらに強めた、「上の図式が可換になるような全単射$\theta_x$の存在」がまさに完全な性質になることを言っている。これは「合成したら何になるか情報を保つ全単射の存在」という意味だ。

$\theta$という同一視の下で、$a$から$x$への射$\phi$の対応物$\theta_x(\phi)$を$\theta_x(\phi)=\phi'$と書こう。ここで、$x$から$y$への射$f\in\text{Hom}_\mathcal{C}(x,y)$と$\phi$を合成すると$f\circ_\mathcal{C}\phi$という$a$から$y$への射が得られる。これは$b$から$y$への射$(f\circ_\mathcal{C}\phi)'$という対応物がある。一方、$\phi'$と$f$を合成すると$b$から$y$への射$f\circ_\mathcal{C}\phi'$が得られる。上の図式が可換とは、これらが等しい$(f\circ_\mathcal{C}\phi)'=f\circ_\mathcal{C}\phi'$ということだ。
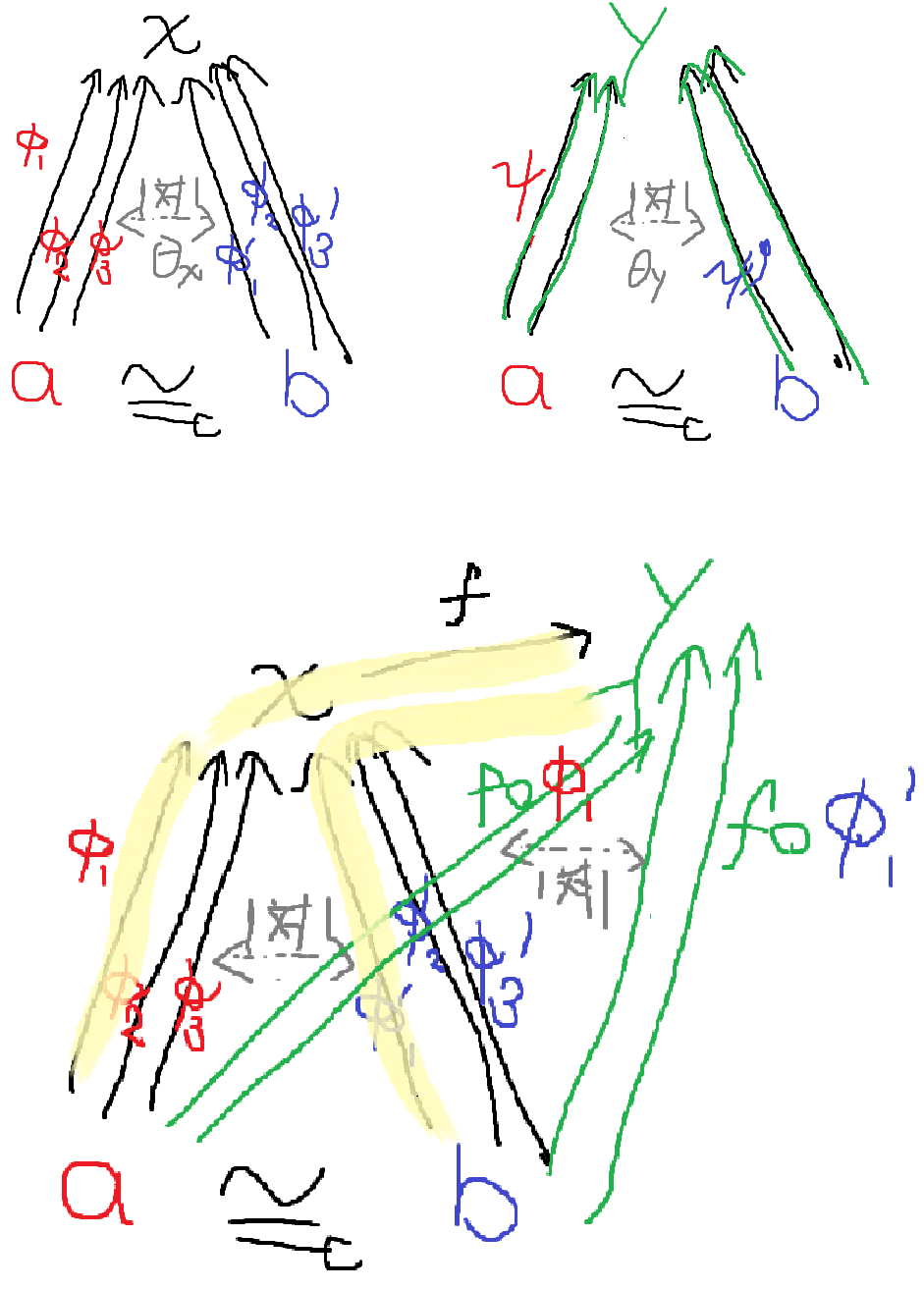この落書きを図と言い張る勇気
つまり、$a\in\mathcal{C}$の完全な性質$\text{Hom}_\mathcal{C}(a,\cdot)$とは自身から伸びる射の本数と合成したら何になるか情報のことであり、自然同型$\text{Hom}_\mathcal{C}(a,\cdot)\cong\text{Hom}_\mathcal{C}(b,\cdot)$とはそれらが同じになるという意味だ。

準同型とは射？

群と群準同型の圏$\textbf{Grp}$における、同型射の存在という同値関係$\cong_\textbf{Grp}$は通常の群同型に一致する。だが、$\textbf{Grp}$以外にも同型射の同値関係$\cong_\mathcal{C}$が群同型と一致するような射の選び方はたくさんある。例えば、射を単射準同型としたり、$\text{dom}$と$\text{cod}$をひっくり返した反対圏$\textbf{Grp}^{\text{op}}$としても、$\cong_\mathcal{C}$は群同型に一致する。同型類を分類するという目的から見れば、射を一つ選ぶことは観察道具を一つ選ぶようなものだ。これらの圏の$\text{Hom}$関手が持ってる個別の情報（$\mathbb{Z}/{7\mathbb{Z}}$から$\mathfrak{S}_5$への射の本数など）は全然違うが、どの圏の$\text{Hom}$関手も完全な性質になっている。
顕微鏡で見ても虫眼鏡で見ても光電子分光で見ても、確かに個別の得られるデータは全然違うが、全部調べきって組み合わせれば最終的に同じものが見える。どれも完全に調べられる観察道具＝完全な性質なら。

群全体$\textsf{Grp}$と群準同型の圏は、$\textbf{Grp}$という表記と共に「群の圏」と呼ばれる。じゃあ対象を距離空間全体$\textsf{Met}$にしたとき、距離空間の圏$\textbf{Met}$に付く"正しい"射は何か？という話題がたまに上がるが、これは世界一頭の悪い話だ。立憲民主党に投票するよりも無駄なことだ。対象が群のとき、群準同型が特別な射であり、正しい射である理由など何もない。射が単射準同型であれop圏の射であれ何であれ、同型射の存在という同値関係$\cong_\mathcal{C}$がちゃんと調べたい同型に一致していればどれも正しい射なのだ。じゃあ、なんで$\textbf{Grp}$って書かれるのか？個人的には、群準同型が誰でも簡単に思いつく「標準的な」射だからなんだと思う。「準同型の最も一般的な概念は射です」と説明する人もいるが、本質を空透かししてるように思う。

伏線回収

最後に、冒頭で挙げた性質を$\text{Hom}$関手で表現してみよう。群$G$の「台集合の濃度」は$|\text{Hom}_\textbf{Grp}( \mathbb{Z},G)|$に等しい。$p$を素数として「位数が１か$p$の元の総数」は$|\text{Hom}_\textbf{Grp}( \mathbb{Z}/{p\mathbb{Z}},G)|$に等しい（位数１とはつまり単位元なので、実質位数$p$の元の総数）。いずれも$\mathbf{Grp}^{\text{op}}$の$\text{Hom}$関手$\text{Hom}_{\textbf{Grp}^\text{op}}(G,\cdot)$が持っている、射の本数の情報だ。

いいねちょうだい🥺