ジャグリングを数え上げます

本記事は 組合せ論 Advent Calendar 2025 の記事となっております．

はじめに

知人の影響からジャグリングなるものをはじめ，もう二年も経ってしまいました．私は生粋の数学人間であったので，本来こんなものと出会うことすらなかったのでしょうが，なぜそんな私がジャグリングを始めたのかといえば，ジャグリングが非常に組み合わせ論との相性が良いということになるでしょう．

本記事の目標はジャグリングを数理モデル化した概念を定め，それがいくつあるのかを数え上げることです．議論の内容は主としてmojによります．

問題設定

この記事では数学的には次の問題を解く事になります．

次の節でこれがどのようにジャグリングと関連しているのかを述べますが，問題のみに興味がある人は次節を飛ばして数学的な議論のみを読むこともできます．

ジャグリングのモデル化

本節ではジャグリングの一種のモデル化としてジャグリングパターンと呼ばれるものを定めます．これが本記事で数え上げる対象となります．
これに関する説明は例えばmathlogの記事ではサイトスワップ，書籍ではmojなどさまざまなところに丁寧なものがあるので，本節ではサイトスワップの性質などには深入りすることなく，数え上げに必要な部分だけを述べようと思います．

ジャグリングといえばさまざまなものが存在しますが，ここではいくつかのボールを投げるジャグリングに限ることにします．モデル化のための仮定として以下を考えます．

この仮定から，ビート$t$で投げたボールがビート$f(t)$で落ちてくるものとして全単射$f: \mathbb Z \rightarrow \mathbb Z$を定めることができます．
仮定の1つ目が考えるべき時刻を整数に制限してよいことを表していて，仮定の2つ目が$f$を全単射と思って良いことを表しています．
さらにボールが落ちてくるのは投げた時刻より後でなければならないので$f(t) > t$であることもわかります．逆にこれを数学的なジャグリングの定義とします

ジャグリングパターンを考える上では，ボール数と周期と呼ばれる二つの特徴量が非常に重要になります．

まずボール数に関して考えます．$f$を定めると，このパターンをジャグリングするのに必要なボールの数は確定します．
$t$から投げたボールは$f(t)$で再び投げられるので，これらの二つのビートで投げられるボールは同じです．このようにして，あるボールがどのビートで投げられるのかというのを$f$から辿ることができるので，そこに出てきたボールの数を数えれば良いです．
数学的に定式化するならば，同じボールが投げられるビートを同値関係$\sim$で表すと，これは$t\sim f(t)$から生成されることがわかり，$\sim$の同値類の数がボールの数を表しているということになります．

次に周期について考えます．ジャグリングパターンは無限に続くジャグリングを表しています．しかし，実用上は流石に無限にジャグリングをするわけにもいかないので，周期性の条件を課すことにより本質的に有限長になっているようなジャグリングパターンのみを考えることがよくあります．
ビート$t$に投げられたボールが$f(t)$でキャッチされるということは，このボールは$f(t)-t$の間だけ飛んでいたということになります（つまりこの時間だけかけて落ちてくるような高さで投げるということです）．これを高さ関数$h(t)$と呼ぶことにしたとき，ジャグリングパターンが周期$p$を持つとは高さ関数が周期$p$の周期関数であること，つまり$h(t)=h(t+p)$を満たすこととして定めます．

以上のことを考えると，問題文はジャグリングの言葉を用いて次のように表すことができます．

数え上げる

問題を再掲します．

証明の鍵となるアイデアは次のようなグラフによる図示を考えることです．

例えば$f(t)=t+3$のダイヤグラムは次のようなグラフになります．

$f(t)=t+3$のダイヤグラム

このとき，問題に登場する同値類はグラフの連結成分と一致します．さらに$h$が正であることは有向辺が値を大きくする方向に貼られていることと，周期性の条件はグラフが周期的であること（つまり，頂点$t$を$t+p$に移す写像がグラフ同型を与えること）と同値です．
逆に，入次数と出次数が全て1の有向グラフがあればそこから写像を復元できますから，そのようなもののうち連結成分が$b$個で有向辺の向きが正しく，周期性の条件を満たすものを与えれば条件を満たす$f$が復元されます．このようなグラフの数を数えることを考えましょう．
以下では，条件から有向辺の向きは明らかなので，向きを明示せずにグラフを考えます．

次のようなカードを考えます．

$b=3$の場合のカード

これは$b=3$の場合で書いており，一般にはそれぞれが$b$本の線からなる$b$種類のカードを考える事になります．
このようなカードを横に並べると例えば次のようになります．

$f(t)=t+3$に対するカードの並べ方

これをダイヤグラムと思うことにすると，この例では$f(t)=t+3$の場合のグラフと等しくなっています．
このようにして作ることのできるダイヤグラムについて調べてみましょう．
まず周期性は，カードの並べ方が周期性を持つかということに対応します．
連結成分の数に関しては，各カードにある$b$本の線がそれぞれ異なる連結成分を構成しているので，グラフは$b$個の連結成分を持つように見えます．
これより，もしも全てのダイヤグラムがカードの並びから構成できるとすれば，求めるものは$b$種類のカードを$p$枚並べる方法に対応するので$b^p$通りが答えになります．

これは概ね正しいですが，少し問題があります．次のようなカードの並べ方を考えましょう．

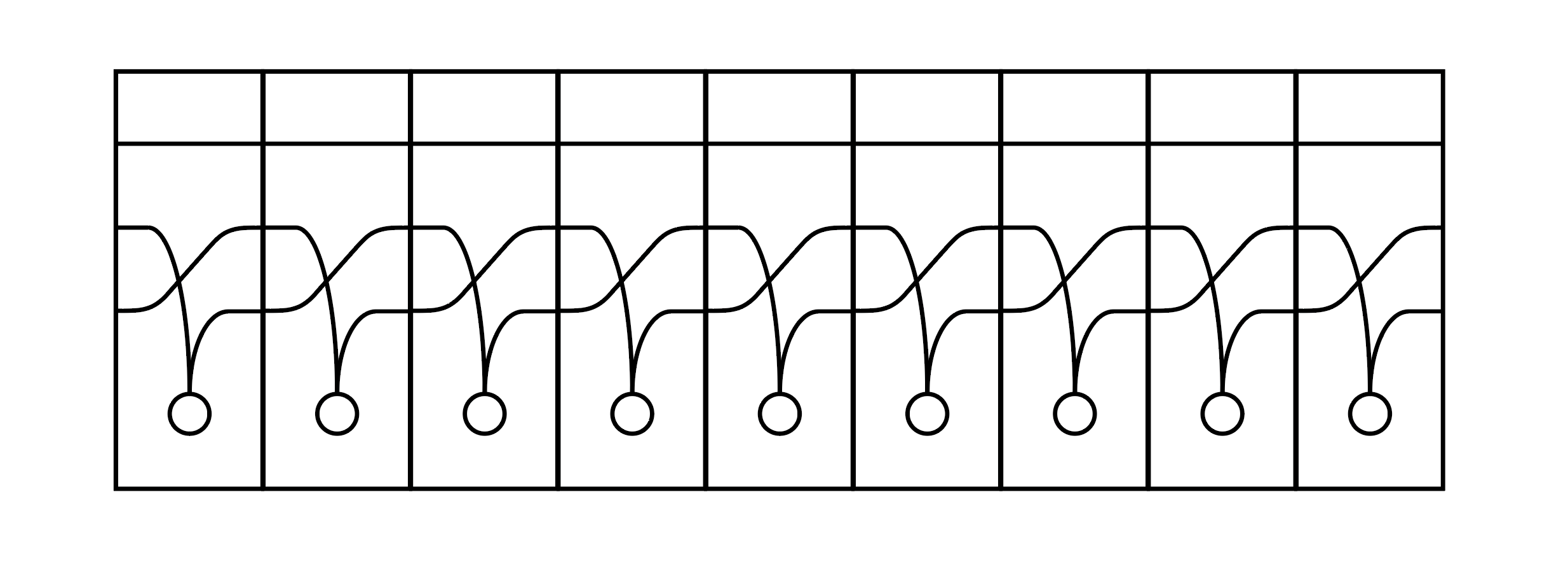うまくいかない例

このとき，一番上の線が一度も頂点に触れることがなく，うまくダイヤグラムを構成できていません．
このような問題を解消するため，もしもこのように一度も頂点に触れない線があった場合はこれを無視してダイヤグラムを構成することにします．すると連結成分の数は無視した線の数だけ減るので，実際には$b$個以下の連結成分を持つダイヤグラムを構成していることになります．

したがって，先ほどの答えを求めるための議論は，もしもこのようなカードの並べ方で連結成分が$b$個以下のダイヤグラムが全て構成できるならば，求めるものは$b^p-(b-1)^p$通りとなる，というように修正されます．

以下ではダイヤグラムが全てカードから構成可能であることを確認します．
それぞれのカードは線を交わらせることにより線を入れ替える操作だと思えるので，ダイヤグラムをうまく変形してカードに存在している形になるように辺の交わり方を調整できれば，ダイヤグラムをカードを使って構成することができます．
ダイヤグラムの各辺がいくつ交点を持つかを確認します．例えば先ほどの$f(t)=t+3$の図であれば，それぞれの辺は下から上に2箇所（図中丸印）で交わり，上から下に2箇所（図中四角印）で交わります.

$f(t)=t+3$のダイヤグラムの交点

このとき，カードで上から下に交わるのは，そのカードで頂点に入る線（下の青線）のみです．

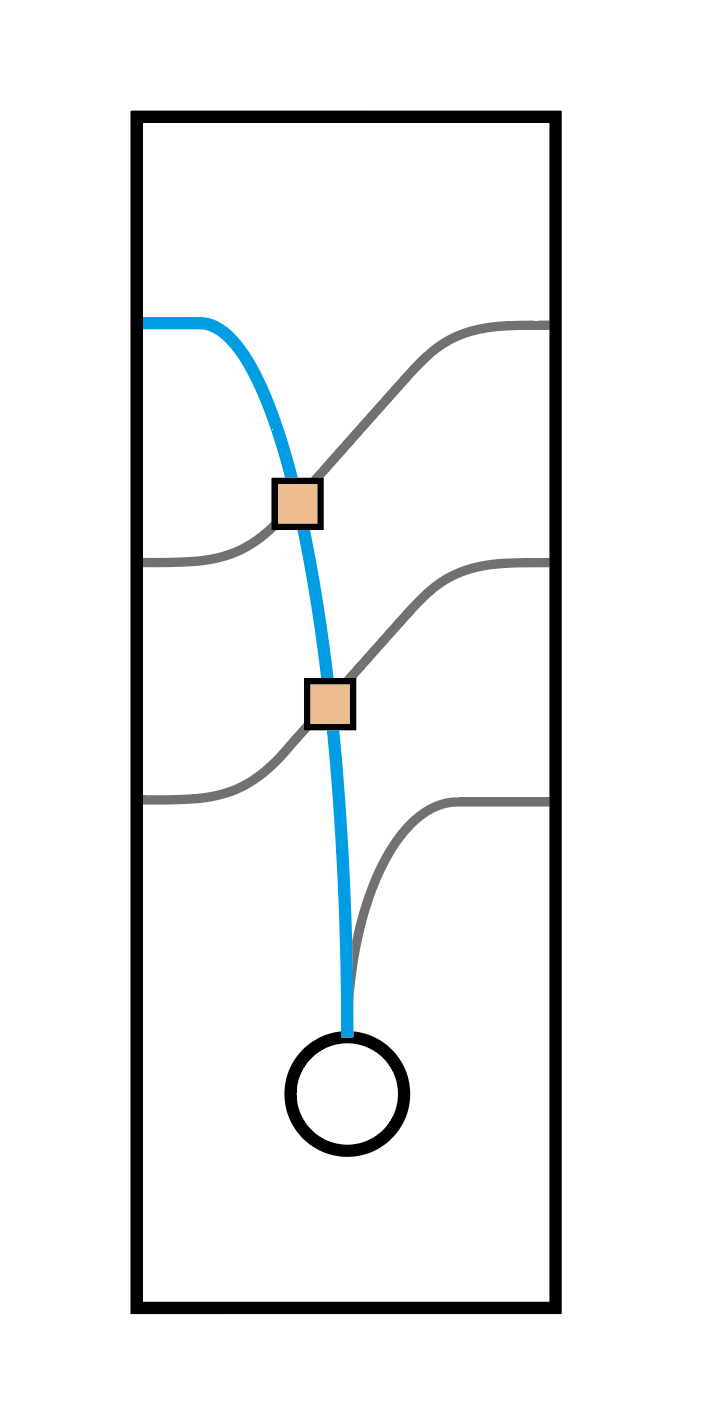カードの交点

したがって，ダイヤグラムで上から下に交わる交点がその辺が入る頂点の真上に並ぶようにダイヤグラムを変形します．このとき，その交点の数と一致するカードを選んで並べていくと元のダイヤグラムと同じ形のグラフがかけることがわかります．したがって任意のダイヤグラムはカードを使って表すことができます．

以上のことから求めるべき$f$の数は$b^p-(b-1)^p$であることがわかりました．

おわりに

今回はジャグリングから出てくる組み合わせの問題について取り上げました．実はジャグリングをしている人と数学が好きな人の共通部分はかなり大きいらしく，サイトスワップ理論と呼ばれるジャグリングパターンについて組み合わせ的に調べる理論はかなりよく調べられています．それによれば，ジャグリングパターンという対象はどうやら数学的に程よく非自明な対象らしく，手頃な道具で議論できる範囲でも簡単なものからとても非自明なところまで，かなり豊かに話題が広がっていることが確認できます．
今回の記事では数え上げの問題設定の理解に必要なほんのわずかな部分しか触れられませんでしたが，もしこの記事で興味を持った方がいれば，非常によくまとまった初歩的な解説としてサイトスワップを，さらに深く学びたい方に向けては古典的によく知られた内容が概ね網羅された本としてmojを読むことをおすすめします．

ジャグリング経験者向けの補足

本節では，サイトスワップを知っている人に向けての補足を述べます．

注意で述べたように，今回の議論の仮定では0が出てくるようなサイトスワップを認めないものとして数え上げを行いました．実は0を含めてもそこまで大きな修正なく同様に数え上げを行うことができます．ここでは変化する点を簡単に述べます．

まず，ボールに触れないビートは$f(t)=t$として定めるとうまくジャグリングパターンの概念を拡張できます．したがって考えるべき問題は元の問題のうち，$h(t)$が正の整数という条件を非負整数という条件に置き換えたものになります．

問題を解くだけであれば，サイトスワップの全ての項に1を加えることを考えれば$b$が1だけ増えた元の正の整数に関する問題に帰着されるので$(b+1)^p-b^p$が答えであることがわかりますが，実はこのような間接的な手法ではなく，0を含むかもしれないダイアグラムをカードによって実現することによって解くこともできます．

ダイヤグラムの上では0を投げるビートは辺が繋がっていない孤立した頂点として表されます．そこでカードととして，線を頂点につながない新たなカードを加えた次のような$b+1$枚を考えることにすれば良いです．

$b=3$におけるカードの拡張

この場合も同様の議論をすることで，ボールが$b$個以下のパターンがカードを並べることで全て実現できるので，$(b+1)^p-b^p$通りのパターンがあることがわかりました．