特異ホモロジーと単体的ホモロジーの同型について
この記事は、Physics Lab. 2025アドベントカレンダーの15日目として書かれたものです。
はじめに
こんにちは、Physics Lab. 2025数理物理班副班長です。アドベントカレンダー15日目、今日は代数トポロジーの話をしたいと思います。今日は真面目にやります[1]。え?Physics Lab.のアドベントカレンダーで「真面目にやる」と言っているのに物理をしていない?そんなことは知りません。
この記事の内容
代数トポロジーの中で、ホモロジー群と呼ばれるものがありますが、これにはいくつかの構成方法があり、それらはどれも同じ結果を返すことが知られています。この記事では、特に単体的ホモロジーと特異ホモロジーの二つの間の同型を示します[2]。簡単のため、ホモロジー群の係数は$\mathbb{Z}$とします。また、この記事では考える空間を少し制限することがあります。
想定している前提知識
単体的ホモロジーの直感の節までは、高校数学でのオイラーの多面体定理を認めます。
基本的な位相空間の知識(位相空間の定義や連続性の定義、コンパクトやHausdorffなど)は仮定します。また、アーベル群の定義くらいは仮定します。この記事の主題は単体的ホモロジーと特異ホモロジーの同型を示すことなので、そこに至るまでの議論で証明を省略している部分があります。
代数トポロジーとは?
代数トポロジーが何かを説明するために、代数トポロジーに何ができるのかを説明します。代数トポロジーとは、二つの位相空間(位相空間を知らない人は図形と思ってください)が「連続的に変形する」ことができるかどうかを判断することができます[3]。よくある話ですが、「穴」があると連続変形することができません。連続変形することができるかどうかは「穴」の数を数えることが重要です。
今まで「連続変形できるかどうか」という話をしてきましたが、どのように判定するのかというと、「連続変形で変わらない量」を調べます。単体的ホモロジーの初めの節で解説しようと思います。
ここで、そもそもなぜ「連続変形できるかどうか」を調べるのか、という疑問があります。実は、「連続変形できるかどうか」は「ゆるい」条件になります。これはたとえば、一点も中身の詰まった球も星形も全部同じとみなすということを意味します。ですが、逆にこの「ゆるい」くくりを構成している全てのもので一致するということは、強力な条件になります。たとえば、物理では、代数トポロジーを用いて、適切な条件で、「磁気モノポールが存在すれば、その磁荷は離散的である[4]」ということが言えます。
単体的ホモロジー
位相空間を単体(三角形や四面体の一般化)によって「分割」し、それによって「穴」の数を数えるのが単体的ホモロジーです。
直感~オイラーの多面体定理~
オイラーの多面体定理は、次のようなことを言っていました。
(面の数)-(辺の数)+(頂点の数)=2
多面体というのは、3次元で「中身の詰まっていない」図形ですね。この「中身がない」ことは穴が一つあるということを意味します。ここで、「中身の詰まった図形」を考えると、次のような量を考えられます。
-(「中身」の数)+(面の数)-(辺の数)+(頂点の数)=1
この「中身」の数は多面体において0なので、多面体と中身の詰まった多面体では右辺に異なる値が現れます。つまり、この量によって穴があるかどうかを判定できる場合があるということです。この量は、ホモロジー群から計算することができる「オイラー標数」と言うものと関係しています。
$\Delta$複体
ここからはちゃんと数学をしていきます。まず単体的ホモロジーの舞台を用意します。普通は単体的複体を用いますが、それを少し一般化した$\Delta$複体を定義します(こちらの方が計算が簡単)。
$p$次元単体とは、以下の集合のことである。
$$\Delta^n=\{(t_0,\cdots,t_n)\in \mathbb{R}^p|\sum_{i=0}^n t_i=1,\ t_i\geq 0\ \text{for all i}\}$$
この図形の各頂点に$v_0,\cdots,v_n$という番号を適当に振る(番号の振り方を一つ固定しておく)。これによってn-単体を$[v_0,\cdots,v_n]$と書くことがある。
$n $-単体から一つ頂点を除くと、残った点から$n-1$単体を一つ作ることができる。これをこのn-単体の表面という。$\Delta$の内核を$\mathring{\Delta}^n$と書く。($\mathring{\Delta}^0=\Delta^0$であることに注意。)
頂点に番号を振ることによって、頂点に「順番」が生まれ、単体に「向き」が定まります。これは、後で「境界」と呼ばれる概念を考えるときに効いてきます。
$X$を位相空間とする。$\Delta$-複体とは、連続写像$\sigma_{\alpha}:\Delta^n\rightarrow X$の族であり、以下の性質を満たすものである(ただし、$\alpha$は$n$の情報も持っている)。
- $\sigma_{\alpha}|_{\mathring{\Delta}^n_{\alpha}}$は単射で、$X$の各点は必ず$\sigma_{\alpha}|_{\mathring{\Delta}^n_{\alpha}}$に含まれる。
- $\sigma_{\alpha}|_{\Delta^n_{\alpha}}$を$\Delta$の表面に制限したものは、ある$\sigma_{\beta}$である。ただし$\Delta^n$の表面を$\Delta^{n-1}$と同一視して書いている。
- $A\subseteq X$が開集合である$\Leftrightarrow$ 各$\sigma_{\alpha}$に対して$\sigma_{\alpha}^{-1}(A)\subset \Delta^p$が開集合。
このような$\Delta$-複体を$\delta(X)$と書くことにする。また、この集合の中で特に$n$-単体からの写像を集めた集合を$\delta_n(X)$と書くことにする(これはこの記事だけのノーテーションなので注意)。
この定義から、$\sigma_{\alpha}|_{\mathring{\Delta}^n_{\alpha}}$が同相写像であることがすぐにわかります[5]。$\Delta$-複体は直感的には、$X$を単体を用いて「分割」しています。$\Delta$-複体は$X$から一意に定まるものではないと言うことを注意してください。
この定義の特徴は、表面において単射を仮定していないことです。これは例えば、$0$-単体(点)が一つあり、$1$-単体がその点を始点と終点とするループであるような場合も許されます。例えば、Kleinの壺を平面上で同一視を入れることによって実現する時、表面において単射を仮定した場合(「単体的複体」を用いた定義)と仮定しない場合では次のような違いがあります[6]。
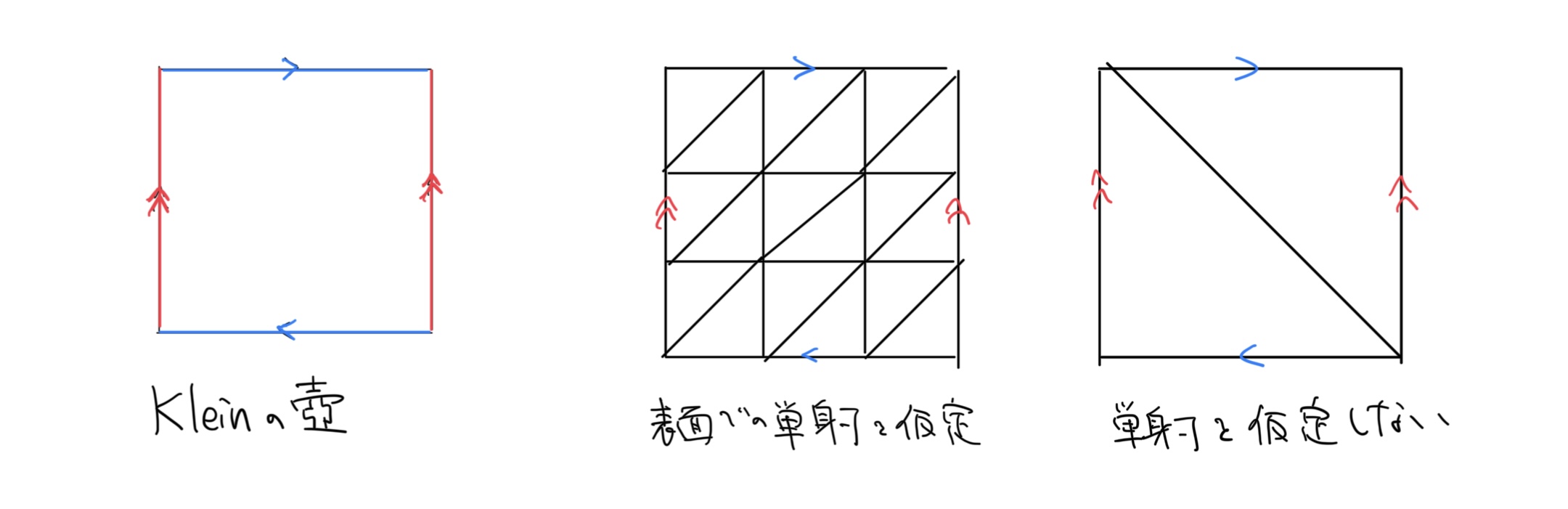
後の定義を見るとわかりますが、分割の個数が多いことはホモロジー群の計算の煩雑さに直結します。分割の個数が少ない$\Delta$-複体はその点優秀と言えるでしょう。
単体的ホモロジー
$\Delta$-複体を用いてホモロジー群を定義します。ここで、のちの議論のために一般化した相対ホモロジーを定義しておきます。
$\Delta$-複体$\delta(X)$を考える。$\Delta_n(X)$を、$\delta_n(X)$で生成される自由アーベル群として定義する。つまり、
$$ \Delta_n(X)\coloneqq \left\{\left.\sum_{\sigma_{\alpha}\in \delta_n(X)} n_{\alpha}\sigma_{\alpha}\right| n_{\alpha}\in \mathbb{Z},\quad \#\{\alpha|n_{\alpha}\neq 0\}<\infty \right\}$$
である。ここで、$\#$は集合の元の個数である。
$\Delta_n(X)$の元を$n$-チェインという。
境界写像$\partial_n:\Delta_n(X)\rightarrow \Delta_{n-1}(X) $を以下のように定義する。
$$\partial_n \sigma_{\alpha}=\sum_{i=0}^n (-1)^i\sigma_{\alpha}|_{[v_0,\cdots\hat{v_i},\cdots,v_n]}$$
ただし、ハットはその頂点を除くことを意味する。
しばしば添え字$n$を省略して単に$\partial$と書く。
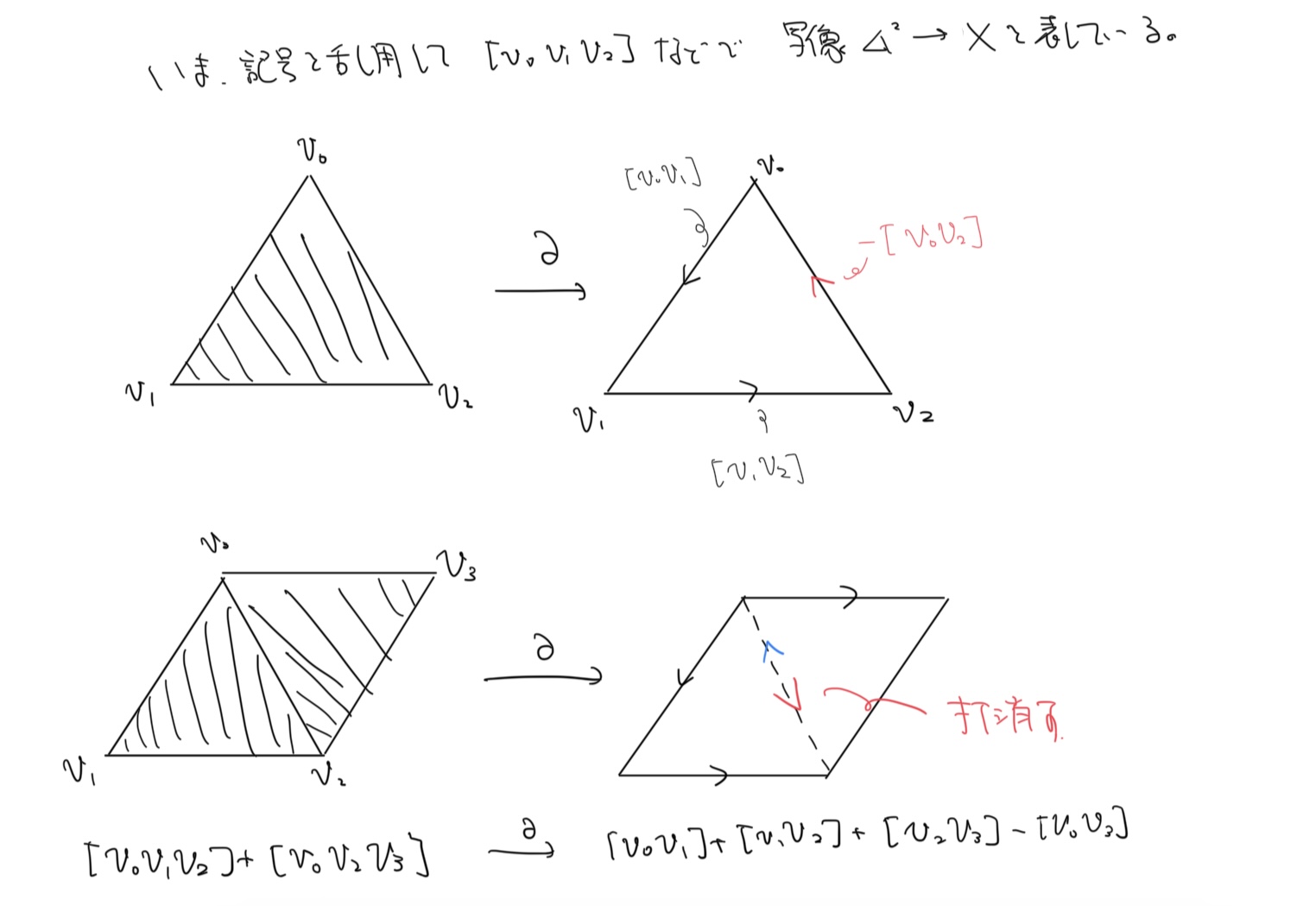 境界写像についての簡単な例
境界写像についての簡単な例
ここで少し直感についての話をしましょう。チェインについて、チェインの和は、そこに現れる係数が$1$のとき、各射像の像(四面体などの$n$-単体に「近い」形になっているはず)の適当に向きを決めた「貼り合わせ」のように思うことができます。これがサイクルであるというのは、その境界がない、つまり「端」がないこととみなせます。「貼り合わせ」が境界であるというのは、その端がなく、中身が詰まっていることとみなせます。
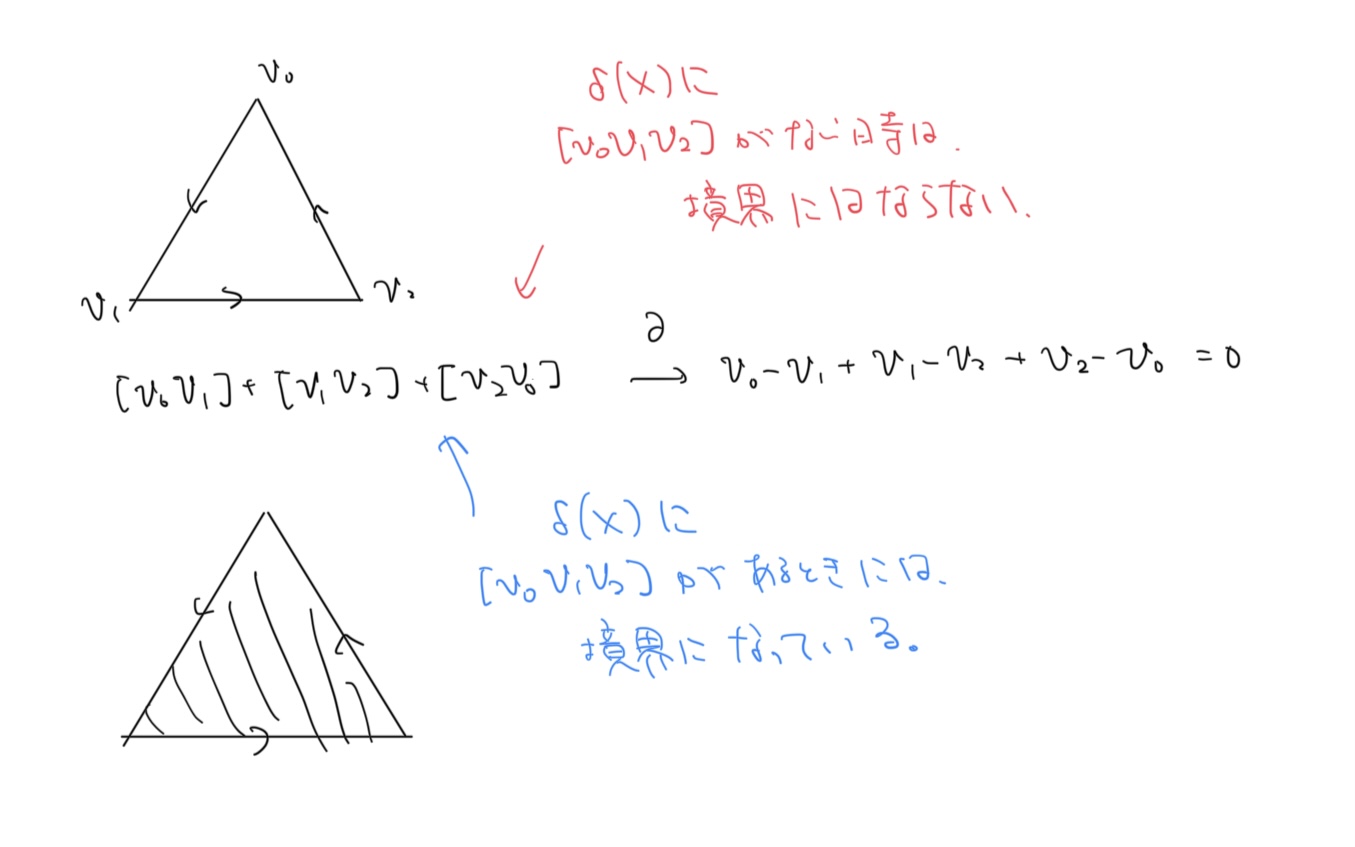 境界になっているかどうかは中身が詰まっているかで決まる
境界になっているかどうかは中身が詰まっているかで決まる
境界写像はアーベル群の間の準同型です。この境界写像が$\partial^2=0$を満たすことが定義による具体的計算によりわかります。これにより、$\ker\partial_n \subset \Im \partial_{n-1}$がわかります。
$\Delta$-複体$\Delta_X$の$n$-次単体的ホモロジー群$H^{\Delta}_n(X)$は、以下のように定義される。
$$H^{\Delta}_n(X)=\ker\partial_n/ \Im \partial_{n-1}$$
$\ker\partial_n$の元を($n$-)サイクル、$\Im \partial_{n-1}$の元を境界と呼ぶ。$H^{\Delta}_n(X)$の元のことをホモロジー類といい、二つの$n$-サイクルの差が境界になっているとき、二つはホモロガスという。
ここで、直感の節とのつながりについて少し言及しておきましょう。まず、一番簡単な四面体を考えてみましょう。四面体には中身が詰まっている時には3-単体から四面体への同相写像$f$が存在するので、その写像とその表面(さらにその表面...)への制限たちからなる$\Delta$-複体を考えることができます。この「中身が詰まっている」かどうかは、3-単体からの同相写像$f$があるかどうかで判断できます。これが存在すれば$f$の表面たちから作られるサイクルは$f$の境界になります(上の定義の前に書いた直感も参照)。よって2次のホモロジー群は自明な群$0$になります。$f$がなければ、四面体の面たちからなるサイクルは境界になっておらず、2次のホモロジー群は$\mathbb{Z}$になります。同様の考察をすると、中身が詰まっていようがいなかろうが、1次のホモロジー群は自明になります。そして0次のホモロジー群は$\mathbb{Z}$です。また、3次以上のホモロジー群は、そもそもサイクルがないので0です。
実は、多面体についてホモロジー群を計算していくと、$H_n(X)=\mathbb{Z}^{b_n}$と表すことができ、$b_n$の交代和$-b_3+b_2-b_1+b_0$(これはオイラー標数と呼ばれます)がオイラーの多面体定理で右辺に現れている量と等しいことがわかります。
さて、次にここから相対ホモロジーというものを定義します。これは次に定義する部分複体を用いて、商群によって定式化されます。
$\Delta$-複体$\delta(X)$を考える。その部分複体とは、$\delta(X)$の部分集合$S$でそれ自体が$\bigcup_{\sigma_{\alpha}\in S}\Im \sigma_{\alpha}$の$\Delta$-複体になっているものを言う。$A=\bigcup_{\sigma_{\alpha}\in S}\Im \sigma_{\alpha}$として$\delta(A)\subset \delta(X)$と書く。
$\Delta_n(A)\subset \Delta_n(X)$は、部分群であるから、商群$ \Delta_n(X)/\Delta_n(A)$を考えられる。
この商群の間に$\partial_n$から自然に誘導される準同型$\bar{\partial}_n:\Delta_n(X)/\Delta_n(A)\rightarrow \Delta_{n-1}(X)/\Delta_{n-1}(A)$がただ一つ存在する。
また、これは$\bar{\partial}^2=0$を満たす。
$\Delta_n(A)\subset \Delta_n(X)$が部分群であることは明らか。また、$\partial$は$\Delta_n(A)$の元を$\Delta_{n-1}(A)$の元に送る(これは$\Delta$-複体の定義からすぐに従う)。そこで、$p_n:\Delta_n(X)\rightarrow \Delta_n(X)/\Delta_n(A)$を商写像とすると、$p_{n-1}\circ\partial_n$は$\ker(p_{n-1}\circ\partial_n) \supset\Delta_n(A) $を満たし、よって商群の普遍性から準同型$\bar{\partial}_n:\Delta_n(X)/\Delta_n(A)\rightarrow \Delta_{n-1}(X)/\Delta_{n-1}(A)$が一意存在する。
このとき、$\ker(p_{n-1}\circ\partial_n) \supset\Delta_n(A) $より、任意の元$[c_n]\in\Delta_n(X)/\Delta_n(A)$[7]に対して$\bar{\partial}[c_n]=[\partial c_n]$が導かれる。ここから、$\bar{\partial}^2[c_n]=[\partial^2 c_n]=[0]$が示される。
これを用いると、上と同様にホモロジー群が定義できます。
$\delta(X)$とその部分複体$\delta(A)$を考える。これらに対して以下のように相対単体的ホモロジー群を定義する。
$$H^{\Delta}_n(X,A)=\ker\bar{\partial}_n/ \Im \bar{\partial}_{n-1}$$
単体的ホモロジー群の時と同様、$\ker\bar{\partial}_n$の元を($n$-)サイクル、$\Im \bar{\partial}_{n-1}$の元を境界と呼ぶ。$H^{\Delta}_n(X)$の元のことをホモロジー類といい、二つの$n$-サイクルの差が境界になっているとき、二つはホモロガスという。
相対単体的ホモロジーにおいて同一視されるのは、境界をとった際に$\delta(A)$に入っているようなものです。つまり、境界が$A$に収まっていればよいというイメージです。
ここまでが単体的ホモロジー群の定義です。単体的ホモロジー群は、以下のような特徴を持ちます。
利点
計算がしやすい。$\Delta_n(X)$の生成元の個数が少ないので、具体的に計算することができます。
欠点
不変性が見えにくい。ホモロジー群が空間に対して定まり、それがホモトピー不変であることを見るには、ホモロジー群が三角形分割によらないことを示さなければなりません。これが大変で、特異ホモロジーとの同型によって間接的に示されます。
特異ホモロジー群
さて、ここからは特異ホモロジー群です。これは、単体的ホモロジー群の$\Delta$-複体の条件を極限まで緩めたようなもので、ホモロジー群のホモトピー不変性など多くのことを導くことができるので、理論的にとても重要です。また、単体的ホモロジー群では、(脚注で少し触れましたが、)考えられる位相空間にある程度の制限がかかっていました。しかし、特異ホモロジー群ではその条件がありません。
では、定義に移りましょう。
$X$を位相空間とする。$n$-単体から$X$への連続写像全体によって生成される自由アーベル群を$C_n(X)$と書く。これの元を$n$-チェインという。つまり、
$$C_n(X)\coloneqq \left\{\left.\sum n_{\alpha}\sigma_{\alpha}\right| n_{\alpha}\in \mathbb{Z},\quad \#\{\alpha|n_{\alpha}\neq 0\}<\infty \right\}$$
である。
ここで、$f$には連続写像であるという条件以外に何も課していないということに注意してください。極端なことを言えば、$n$-単体から$X$の中の一点に送る写像も$n$-チェインです。
定義を見ればわかりますが、この$C_n(X)$は非常に大きなAbel群になります。
次に、境界写像を定義しましょう。これは前とほぼ同じです。
境界写像$\partial_n:C_n(X)\rightarrow C_{n-1}(X) $を以下のように定義する。
$$\partial_n \sigma_{\alpha}=\sum_{i=0}^n (-1)^i\sigma_{\alpha}|_{[v_0,\cdots\hat{v_i},\cdots,v_n]}$$
ただし、ハットはその頂点を除くことを意味する。
しばしば添え字$n$を省略して単に$\partial$と書く。
これも$\partial^2=0$を満たし、$\ker\partial_n\subset \Im \partial_{n-1}$が成立します。
位相空間$X$の$n$-次特異ホモロジー群$H_n(X)$は、以下のように定義される。
$$H_n(X)=\ker\partial_n/ \Im \partial_{n-1}$$
$\ker\partial_n$の元を($n$-)サイクル、$\Im \partial_{n-1}$の元を境界と呼ぶ。$H_n(X)$の元のことをホモロジー類といい、二つの$n$-サイクルの差が境界になっているとき、二つはホモロガスという。
単体的ホモロジー群の時と同様に、相対ホモロジー群を定義できます。
$X$を位相空間、$A$をその部分空間とする。
$C_n(A)$は$C_n(X)$の部分群である。よって商群$ \Delta_n(X)/\Delta_n(A)$を考えられる。
この商群の間に$\partial_n$から自然に誘導される準同型$\bar{\partial}_n:\Delta_n(X)/\Delta_n(A)\rightarrow \Delta_{n-1}(X)/\Delta_{n-1}(A)$がただ一つ存在する。
また、これは$\bar{\partial}^2=0$を満たす。
$\partial$が$C_n(A)$の元を$C_{n-1}(A)$に写すことを示せばあとは前の命題と同様に従う。ところが、このことは$C_n(A)$の定義と境界の定義を考えると自明である。
$X$を位相空間、$A$をその部分空間とする。これらに対して以下のように相対特異ホモロジー群を定義する。
$$H^{\Delta}_n(X,A)=\ker\bar{\partial}_n/ \Im \bar{\partial}_{n-1}$$
特異ホモロジー群の時と同様、$\ker\bar{\partial}_n$の元を($n$-)サイクル、$\Im \bar{\partial}_{n-1}$の元を境界と呼ぶ。$H^{\Delta}_n(X)$の元のことをホモロジー類といい、二つの$n$-サイクルの差が境界になっているとき、二つはホモロガスという。
特異ホモロジー群は非常に大きなAbel群を非常に大きなAbel群で割ったものとして定義されており、計算が非常に大変です。試しに一点集合$*$で計算してみてください。これは一点集合への写像が一つしかないことから簡単に計算できて、$H_0(*)=\mathbb{Z},\quad H_n(*)=0\ (n\neq 0)$となるはずです。$C_n(*) (n\neq 0)$が$0$ではないことに注意してください。
ここまで二つのホモロジー群を定義してきました。二つのホモロジー群は全く異なるように見えます。特に、特異ホモロジー群は非常に大きなAbel群を非常に大きなAbel群で割ったものとして定義されており、どのような形になるのか見当もつきません。しかし、初めに述べたように、これら二つのホモロジー群は一致するのです。なんとも不思議ですね。
特異ホモロジーの不変性について
連続変形について
二つのホモロジー群の同型に進む前に、連続変形による不変性について触れておきます。この節では$I$と言ったら閉区間$[0,1]$を指します。
位相空間$X,Y$を考える。連続写像$f,g:X\rightarrow Y$がホモトピックとは、ある連続写像$h:X\times I\rightarrow Y$が存在して$h(x,0)=f(x),\quad h(x,1)=g(x)$を満たすことである。このとき$f\simeq g$と書く。
写像$f:X\rightarrow Y$がホモトピー同値であるとは、連続写像$g:Y\rightarrow X$が存在して、$f\circ g\simeq \mathrm{id}_Y$かつ$g\circ f\simeq \mathrm{id}_{X}$を満たすことである。また、このとき、空間$X,Y$もホモトピー同値という。
$X$を位相空間、$A$をその部分空間とする。$r:X\times I\rightarrow X$が強変位レトラクトであるとは、
- $r(x,0)=\mathrm{id}_X$
- $r(x,1)\in A$
- $\forall t\in I,\forall x\in A, \quad r(x,t)=x$
を満たすものである。
強変位レトラクトの$I$の成分を$1$に固定したものは、明らかに$A$と$X$のホモトピー同値です。これが我々が日常で思い浮かべる「連続変形」に近いでしょう[8]。
特異ホモロジーの不変性
この節では特異ホモロジーの位相不変性について触れます。特異ホモロジーは、定義からほぼ即座にいそう不変性が出てくると言う点で優秀です。さらにホモトピー不変(つまりホモトピー同値な空間に対して同型)と言う性質もあるのですが、こちらは紹介するだけで証明は省略しようと思います[9]。
$X,Y$を位相空間とする。$f:X\rightarrow Y$を連続写像とする。このとき、任意の$\sigma:\Delta^n\rightarrow X$に対して、写像$f$を合成することで$f\circ \sigma:\Delta^n\rightarrow Y$を得られる。これを拡張することで、準同型$f_{\sharp}:C_n(X)\rightarrow C_n(Y)$を得る[10]。$f_{\sharp}$を$f$から誘導される準同型という。
この誘導される準同型は以下のような性質を満たします。
$X,Y,Z$を位相空間とし、$f:X\rightarrow Y, g:Y\rightarrow Z$とする。
- $ (g\circ f)_{\sharp}=g_{\sharp}\circ f_{\sharp}$
- $(\mathrm{id}_{X})_{\sharp}=\mathrm{id}_{C_n(X)}$
- $f$が同相写像の時$f_{\sharp}^{-1}=(f^{-1})_{\sharp}$
1,2. 定義からすぐに示される。
3. 1で$g=f^{-1}$として、2.を使うと示される。
また、定義を具体的に書き下してみると、次がわかります。
$f_{\sharp}$は$\partial$と交換する:$f_{\sharp}\partial=\partial f_{\sharp} $
ここで、異なる空間の$\partial$を同じ記号で表していることに注意。
$X,Y$を位相空間とする。$f:X\rightarrow Y$を連続写像とする。
このとき、$f$から誘導される準同型$f_{\sharp}:C_n(X)\rightarrow C_n(Y)$から、準同型$f_*:H_n(X)\rightarrow H_n(Y)$が誘導される。
こちらの$f_*$のことも、$f$から誘導される準同型と呼びます。記号が異なるので、混同することは少ないと思います。
命題4より、$f_{\sharp}$はサイクルをサイクルに送り、境界を境界に送る。よって、$\ker\partial_n$から$H_n(Y)$への商写像$p_n$を考えると、$\ker p_n\circ f_{\sharp}\supset \Im\partial_{n-1} $であり、したがって、一意的に準同型$f_*:H_n(X)\rightarrow H_n(Y) $が存在する。
この命題から特異ホモロジー群の位相不変性が導かれます。
位相空間$X$と$Y$が同相なら、任意の$n\in \mathbb{N}$に対して$H_n(X)\cong H_n(Y)$。
$f:X\rightarrow Y$を同相写像とする。$f_*:H_n(X)\rightarrow H_n(Y)$があるが、$f_*^{-1}=(f^{-1})_*$が存在するから、$H_n(X)\cong H_n(Y)$である。
さらに強く、ホモトピー不変性も成り立ちます。
位相空間$X$と$Y$がホモトピー同値なら、任意の$n\in \mathbb{N}$に対して$H_n(X)\cong H_n(Y)$。
証明は、$f$と$g$がホモトピックなら、同じ準同型$f_*=g_*$を誘導することを示します。このために、$\Delta^n\times I$を単体で分割し、その単体たちによって、$f_{\sharp}$で送ったチェインを少しずつ$g_{\sharp}$で送ったものに変形します。この変形を行う写像$P$が境界写像に対して良い性質$\partial P+P\partial =g_{\sharp}-f_{\sharp}$を満たすことから、$f_*=g_*$が導かれます。
今最後に使った性質は重要なので、定義だけしておきます(この記事ではほぼ使いません)。
連続写像$f,g$から誘導される$f_{\sharp},g_{\sharp}$に対して$\partial P+P\partial =g_{\sharp}-f_{\sharp}$を満たす写像$P$をチェインホモトピーという。
今の定義式で、始域をサイクルに制限すると$P\partial$が$0$になり、終域側で「境界全体の集合で割る」と言う操作をする商写像$p_n$を合成すると、$p_n\partial=0$だから、命題5での構成により$f_*=g_*$となります。
長完全列
目標としている特異ホモロジーと単体的ホモロジーの同型を示すためには、長完全列と呼ばれるものを用いるので、ここでその定義をします[11]。この節では、特異ホモロジーと単体的ホモロジーの両方に対して成り立つ性質を議論します。ノーテーションがよくないですが、$C_n(X)$と書いたら、$C_n(X)$または$\Delta_n(X)$を表し、$H_n(X)$は特異または単体的ホモロジー群を表します。また、$C_n(X,A)$と書いたときには、$\Delta$-複体を考える際は$A$が$X$の部分複体であることを仮定しています。
短完全列とは、次のようなアーベル群などの集合[11]と写像の列で、各写像$d_i$に対して$\ker d_i=\Im d_{i-1}$が成り立つことを言う。
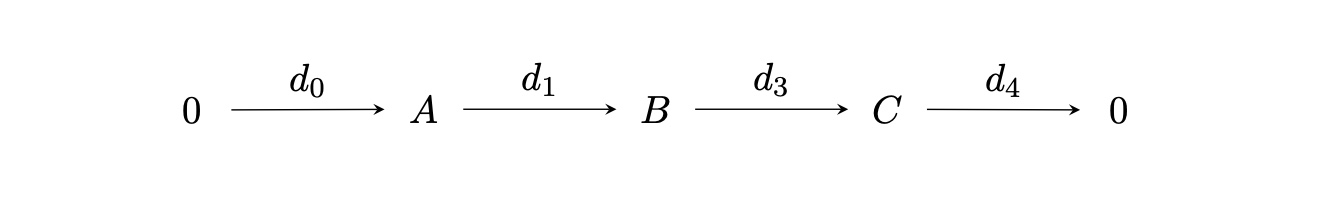 短完全列
短完全列
長完全列とは、同様にアーベル群などの集合と写像の列で、各写像$d_i$に対して$\ker d_i=\Im d_{i-1}$が成り立つことを言う。
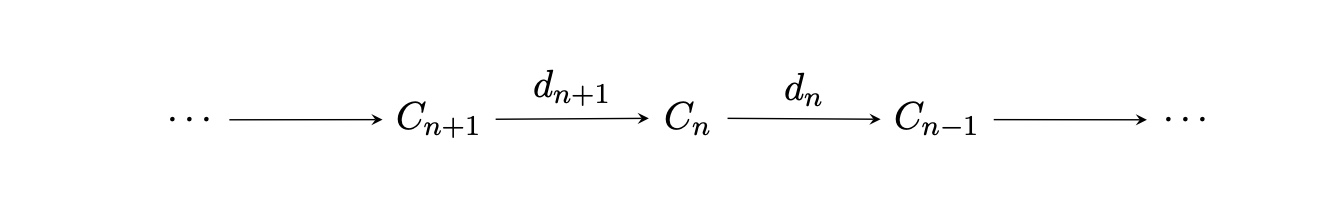 長完全列
長完全列
定義から自明に以下が従います。
以下の短完全列を考える。
このとき、$f$は単射であり、$g$は全射である。
この節では、一定の条件のもとでホモロジー群とそれを結ぶ準同型によって完全列が構成されることを見ます。完全列はホモロジー群について多くのことを教えてくれます。例えば、「複雑な形」をした位相空間を二つの開集合で被覆した時、その二つの被覆についてのホモロジー群から元の位相空間のホモロジー群の情報を得ることができます(Mayer-Vetoris完全列など)。この節では、後で使うために、相対ホモロジー群とホモロジー群からなる長完全列の存在について述べます。
長完全列は、名前の通り長いので、存在を示すのは難しそうに見えるかもしれません。しかし、次のように、短完全列から長完全列を構成することができます。
$A,B,C$を位相空間とする。任意の$n\in \mathbb{N}$に対して、$A,B,C$のチェイン全体の集合からなる短完全列が以下のように与えられるとする。ただし、$f_{n},g_{n}$は$f_{n-1}\partial =\partial f_{n},\ g_{n-1}\partial =\partial g_{n}$を満たす準同型である。
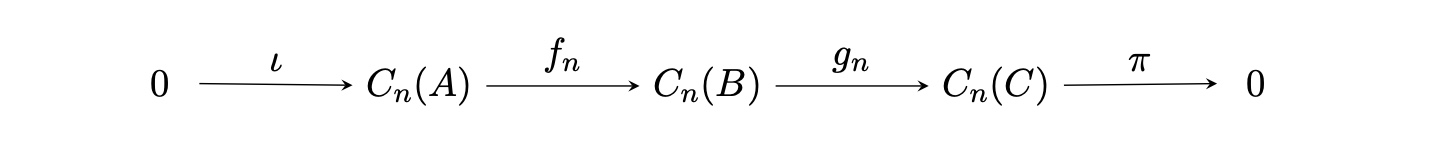
このとき、準同型$\delta:H_n(C)\rightarrow H_{n-1}(A)$が存在して、以下のような長完全列をなす。

ここで、$f_*,g_*$は、$f_n, g_n$から命題5の議論と同様に作られる準同型である。
証明は省略します。これは位相的なことは一切必要なく、純粋に代数的な議論で示すことができます[12]。証明はしませんが、$\delta$の構成だけ示しておきましょう。
$[c_n]\in H_n(C)$を考える。$\partial c^p=0$である。$g_{n}$は全射より、ある$b_n\in H_n(B)$が存在して$ g_nb_n=c_n$を満たす。可換性から、$g_{n-1}\partial b_n=\partial g_{n}b_n=\partial c_n=0$である。よって$\partial b_n$は$\ker g_{n-1}=\Im f_{n-1}$に入っている。したがってある$a_{n-1}$が存在して、$\partial b_n=f_{n-1}a_{n-1}$である。再び可換性と$f_{n-1}$の単射性から$f_{n-1}\partial a_{n-1}=0\Rightarrow \partial a_{n-1}=0$。よって$\delta[c_n]=a_{n-1}$とする。
Zig Zag Lemmaを用いると、以下のような長完全列の存在を示すことができます。
以下のような長完全列が存在する。
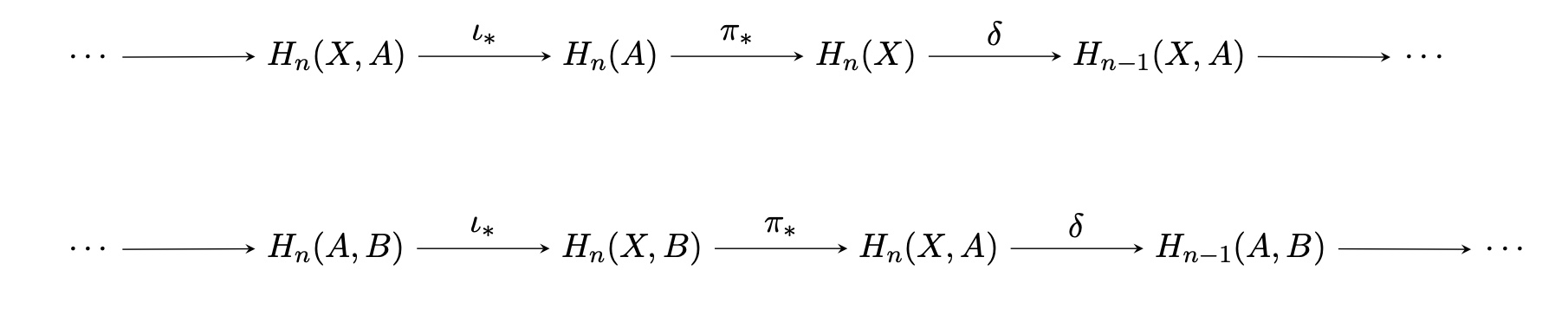
Zig Zag Lemmaの仮定を示せば良い。以下のような短完全列があることを言う。
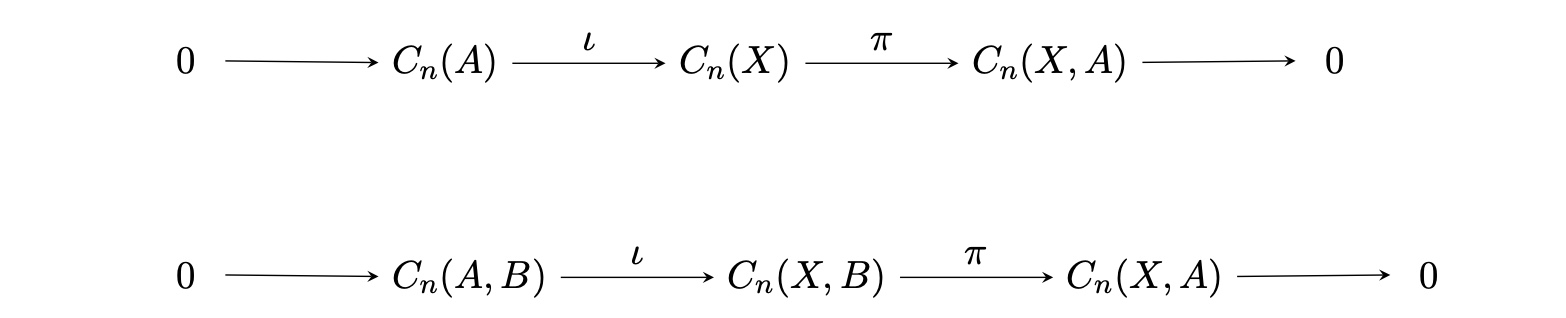
ここで、$\iota$は包含写像、$\pi$は商写像である。$\iota$の単射性は明らか。\piが全射であることも商写像だから、明らか。
残りは$\ker \pi= \Im \iota$を示さなければならないが、これは$C_n(X,A)$の定義と$\iota,\pi$の定義からすぐにわかる。
良いペア
特異ホモロジーと単体的ホモロジーの同型の証明にあたって、必要なことがもう一つあります。この節に関しても証明は行いません[13]。また、ノーテーションを元に戻します。
$X$を位相空間、$A$をその空でない閉集合であり、ある$X$内の近傍の強変位レトラクトになっているとする。このとき組$(X,A)$を良いペアという。
良いペアについて、以下のような命題が成立します。
良いペア$(X,A)$に対して、商写像$q:X\rightarrow X/A$は同型$q_*:H_n(X,A)\rightarrow H_n(X/A,A/A)$を誘導する。右辺は
$$H_n(X/A,A/A) \cong H_n(X/A) \quad (n\neq 0)$$
$$H_0(X/A,A/A)\oplus \mathbb{Z}\cong H_0(X/A)$$
を満たす。
これは以下の定理を用いて証明されます。
$Z\subset A\subset X,\quad Z\subset \mathring{A}$とする。
包含写像$(X\backslash Z, A\backslash Z)\hookrightarrow (X,A)$は同型$H_n(X\backslash Z, A\backslash Z)\rightarrow H_n(X,A)$を誘導する。
すなわち、$A,B\subset X,\quad \mathring{A}\cup \mathring{B}=X$のとき、包含写像$(B,A\cap B)\rightarrow (X,A)$は同型$H_n(B,A\cap B)\rightarrow H_n(X,A)$を誘導する。
定理(の前半)が言っていることは、$X,A$のどちらにも含まれる部分を取り除いても、相対ホモロジー群は変化しないと言うことです。これは$C_n(X,A)$の定義が$C_n(A)$で割っているのだから当たり前に見えるかもしれませんが、証明はかなり大変です。
証明には重心細分というものを用います。
単体$[v_0k,\cdots,v_n]$の点は$\sum_{i}t_iv_i\quad (\sum_it_i=1,t_i\geq 0)$である。各$i$に対して重心とは、点$b=\sum_i\frac{1}{n+1}v_i$のことである。
$[v_0,\cdots,v_n]$の重心細分は帰納的に定義される。$[v_0,\cdots,v_n]$の重心細分とは$n$-単体$[b,w_1,\cdots,w_{n-1}]$たちのことである。ただし、ここで$[w_1,\cdots,w_{n-1}]$は$[v_0,\cdots,\hat{v}_i,\cdots,v_n] $のある重心細分である。
証明の方針だけ述べておきます[14]。
この命題において、直感的には、単体からの写像で$C_n(A)$と$C_n(B)$に跨っているようなものが問題になりそうです。そこで、重心細分を用いて単体を小さく分割していくことにより、像が$A$または$B$の少なくとも一方に入るようにします。その際、ホモロジー群を変化させないように、チェインホモトピーで結ばれるように工夫します。
重心細分の性質の証明
重心細分した単体の直径が元の$\frac{n}{n+1}$以下になることを示す。これは重心細分を繰り返すと単体の「大きさ」が0にいくと言う点で重要である。線形なチェインに対する重心細分
まず、ユークリッド空間内の凸集合$Y$への線型写像$\sigma:\Delta^n\rightarrow Y$から生成される自由アーベル群$LC_n(Y)$に対する重心細分準同型$S:LC_n(Y)\rightarrow LC_n(Y)$を定義する。これは$\sigma:\Delta^n\rightarrow Y$を、始域を$ \Delta^n$の重心細分(を単体とみなしたもの)に制限した写像たちの和によって与えられる。これは$S\partial =\partial S$を満たす。$S$に対して準同型$T:LC_n(Y)\rightarrow LC_{n+1}(Y)$で$T\partial +\partial T=\mathrm{id}-S$を満たすものを定義できる。一般のチェインに対する重心細分
一般の$\sigma:\Delta^n\rightarrow X$に対して$S$の作用を$S\sigma=\sigma_{\sharp}S\ \mathrm{id}_{\Delta^n}$によって定義する。これは2.での性質と同じ性質を満たし、2.と同様$T$が存在する。重心細分の繰り返し
重心細分を繰り返すと、1.での結果からその像は一般に「縮小」される。そして$S^m\sigma$を線型結合のように書いた時の「基底」それぞれの像が$A$または$B$のいずれか一方に含まれるようにする。$\sigma$に$m(\sigma)$回$S$を作用させるとそのようになるとした時、$D:C_n(X)\rightarrow C_{n+1}(X)$を$D\sigma=\sum_{i=0}^{m(\sigma)}TS^i\ \sigma$と定義する。さらに、包含写像$\iota:C_n(A)+C_n(B)\rightarrow C_n(X)$に対して$D\partial +\partial D=\mathrm{id}-\iota\rho$と$\rho \iota=\mathrm{id}$を満たすように$\rho:C_n(X)\rightarrow C_n(A)+C_n(B)$を定義する。主張の証明
$\rho$ から$(C_n(A)+C_n(B))/C_n(A)\hookrightarrow C_n(X)/C_n(A)$が誘導される。これはホモロジー群の同型を誘導する。また、包含写像から誘導される$C_n(B)/C_n(A\cap B)\rightarrow (C_n(A)+C_n(B))/C_n(A)$も同型である。これらから主張が従う。
以下の可換図式を使う。$V$を$A$の近傍で$A$への強変位レトラクトが存在するものとする。
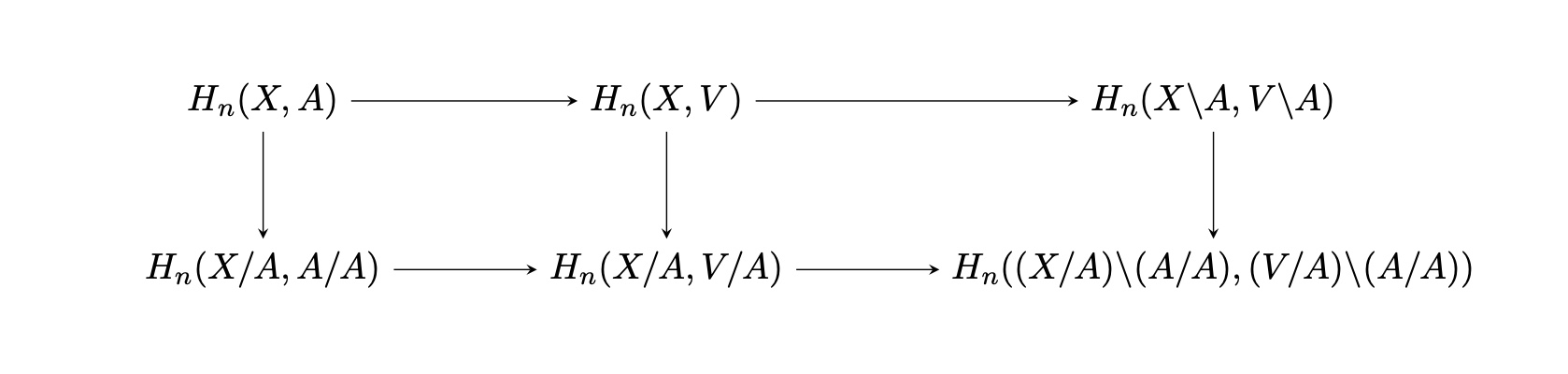
左上の矢は$(X,V,A)$についての完全列から同型である。左下も、$V$から$A$への強変位レトラクトが$V/A$から$A/A$への強変位レトラクトを誘導するから、同型となる。右側の横向きの矢二つはExcision Lemmaより同型である。さらに右側の$q_*$もExcision Lemmaにより同型である。よって最も左の$q_*$も同型である。
補題3と命題4を使うと次のような完全系列が導かれます。
以下のような完全系列が存在する。
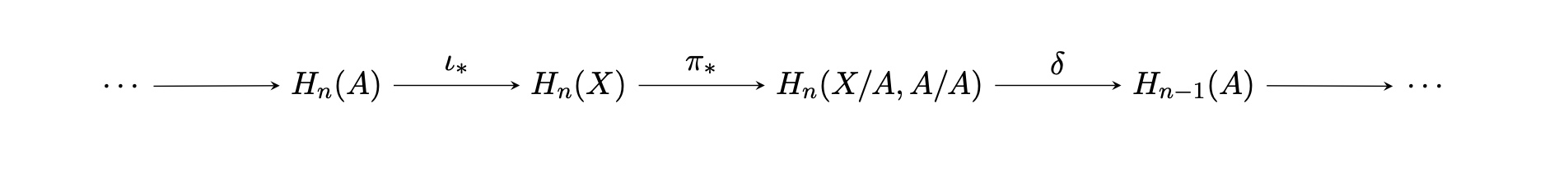
命題4での$H_n(X,A)$を同型によって$H_n(X/A,A/A)$に置き換えれば良い。
ここから球面の特異ホモロジー群を計算可能です。
$n\neq 0$とする。$H_m(S^n)=0\quad (m\neq 0,n)$であり、$H_m(S^n)=\mathbb{Z}\quad(m=0,n)$である。
$S^n=D^n/S^{n-1}$($D^n$は$n$次元球)であることに注意する。$D^n$は可縮だから$0$次以外のホモロジー群は自明であり$H_0(D^n)=\mathbb{Z}$、命題13の長完全列により、$m\neq 0$で$H_m(S^n)\cong H_m(S^n,S^{n-1}/S^{n-1})\cong H_{m-1}(S^{n-1})$を得る。$H_n(S^0)$を考えるとこれは$H_0(S^0)$のみ$\mathbb{Z}^2$でそれ以外は$0$である($S^0$は2点からなる集合)。$H_0(D^n)=\mathbb{Z}$に注意すると$H_1(S^1)=\mathbb{Z}$であり、よって$n$についての帰納法から主張が従う。
さらに、空間のウェッジ積について以下の性質が成り立ちます。
$\bigvee_{\alpha}X_{\alpha}$を考える。基点$x_{\alpha}$に対して$(X_{\alpha},x_{\alpha})$が良いペアなら、$H_n(\bigvee_{\alpha}X_{\alpha},[x_{\alpha}])\cong \bigoplus_{\alpha}H_n(X_{\alpha},\{x_{\alpha}\})$である。
命題4において$(X,A)=(\coprod_{\alpha}X_{\alpha},\coprod_{\alpha}\{x_{\alpha}\})$とすれば従う。
$\Delta$-複体$\delta(X)$がある。自然数$k$をひとつ固定する。$n\leq k$とし、$\delta(X)$の元で$n$-単体からの写像であるようなもの全体を集める。これらの写像による像の合併を$k$-スケルトンといい、$X^k$で書く。
要するに、$\Delta$-複体が点、辺、面...というように下の次元から$X$を「組み上げていく」ようなものであると解釈すると、その途中段階が$k$-スケルトンです。このスケルトンについて以下のような性質が成り立ちます。
$(X^k,X^{k-1})$は良いペアである。
$X^{k-1}$の$X^k$での近傍で、$X^{k-1}$への強変位レトラクトが存在するようなものを構成すれば良い。これは任意の$\sigma:\Delta^k\rightarrow X$に対して十分小さい$\varepsilon$をとり、$U\coloneqq\{(t_0,t_1,\cdots,t_n)\subset \Delta^n|\exists i\in\{0,\cdots,n\}, t_i<\varepsilon\}$を考えると、$\bigcup_{\alpha}\sigma_{\alpha}(U)$($\sigma_{\alpha}$は$n$-単体からの写像)として近傍が構成できる。$U$から$\partial \Delta^n$への強変位レトラクトと$\sigma_{\alpha}$を合成することで$\bigcup_{\alpha}\sigma_{\alpha}(U)$から$X^{k-1}$への強変位レトラクトが構成できる。
特異ホモロジーと単体的ホモロジー群の同型
さて、ようやく本題です。
$$H^{\Delta}_n(X)\cong H_n(X)$$
を示しましょう。このためには今までの議論に加えて、補題が一つ必要です。
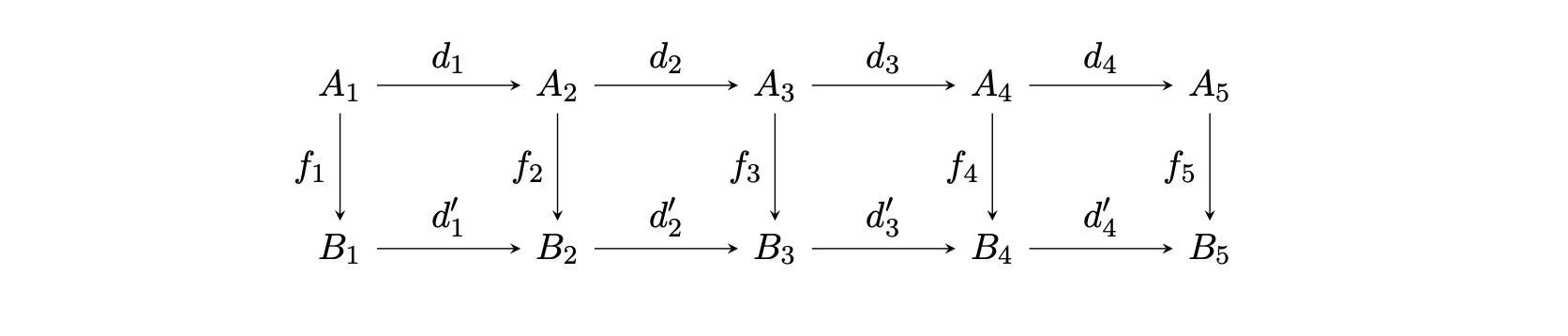
次の補題を認めるかもしれないし証明するかもしれません(公開日までのキャパによります)認めます。証明は地味な図式追跡によって行われます。
以下のような可換図式がある。それぞれ$A_1$から$B_5$まではアーベル群であり、それらを結ぶ矢印は準同型である。このとき、$f_1,f_2,f_4,f_5$が同型なら、$f_3$も同型。
位相空間$X$には$\Delta$-複体$\delta(X)$が存在し、「ある自然数nが存在して、$N\geq n$ならば$\Delta_N(X)=\emptyset$である」とする(つまり有限次元である)。このとき、
$$H^{\Delta}_n(X)\cong H_n(X)$$
が成立する。
これは実はもっと一般に無限次元や相対ホモロジー群で成り立つのですが、その証明は上の主張を頑張って拡張していく感じになります。正直無限次元を扱うことはそんなにない(?)と思うので、今回は有限次元のみ証明しておきます。
それでは証明に移りましょう。
次のような長完全列を考え、Five lemmaを用いて証明を行う。

横の写像は長完全列の構成で与えられる写像である。縦向きの写像は、次のように与えられる。$\Delta_n(X^k)$の元は$n $-単体からの連続写像であることに注意すると、$\Delta_n(X^k)$は$C_n(X^k)$の部分群である。そこで、包含写像$i_n:\Delta_n(X^k)\rightarrow C_n(X^k)$が存在する。また、任意の$[c_n]\in \Delta_n(X^k,X^{k-1})$に対して、$[c_n]\in \Delta_n(X^k)$を$[c_n]\in C_n(X^k)$に送る準同型が存在する。これのwell-definednessは、任意の$d_{n}\in \Delta_{n}(X^{k-1})$にたいして、$c_n+d_n$を包含写像で送ると$c_n+d_n\in C_n(X^{k})$となる。ここで$d_n\in C_{n-1}(X^{k-1})$であることから、$d_n$によらず$[c_n]\in C_n(X^k,X^{k-1})$が定まる。
まず、$H^{\Delta}_n(X^k,X^{k-1})$と$H_n(X^k,X^{k-1})$を結ぶ写像が同型であることを示そう。左辺を調べる。$n< k$のとき、$\Delta_n(X^k)=\Delta_n(X^{k-1})$(これは$X^k$の定義から)。同様に定義から$n>k$のとき$\Delta_n(X)=\emptyset$であるから、$H^{\Delta}_n(X^k,X^{k-1})=0$である。これに対して$n=k$のとき、$H^{\Delta}_n(X^n,X^{n-1})$は境界をとって$\Delta_{n-1}(X^{k-1})$に入る元全体であるから、定義から$\Delta_{n}(X^{k},X^{k-1})$である:$H^{\Delta}_n(X^n,X^{n-1})=\Delta_{n}(X^{n},X^{n-1})$。次に右辺を調べる。このためには、次の写像を考える。$\Phi=\coprod_{\alpha}\sigma_{\alpha}:\coprod_{\alpha}\Delta_{\alpha}^k\rightarrow X^k$。これは同相写像$\coprod_{\alpha}\Delta_{\alpha}^k/\coprod_{\alpha}\partial\Delta_{\alpha}^{k}\cong X^k/X^{k-1} $を誘導する。さらに、$\coprod_{\alpha}\Delta_{\alpha}^k/\coprod_{\alpha}\partial\Delta_{\alpha}^{k}\cong \bigvee_{\alpha}S^k_{\alpha}$である。これと、$(X^k,X^{k-1})$が良いペアであることを用いると、$H_n(X^k,X^{k-1})\cong H_n(X^k/X^{k-1},X^{k-1}/X^{k-1})$。よって$n\neq k$のときは$H_n(X^k,X^{k-1})=0$であり、$n=k$のときは$H_n(X^n,X^{n-1})=\bigoplus_{\alpha}\mathbb{Z}$(命題8)。ここで、$\alpha$は$\delta(X)$に属する$\Delta^n$からの写像のラベルである。以上で縦の写像が同型であることが示せた。
今の結果を用いると、$k$に関する帰納法により定理を示すことができる。
$k=0$のとき、$H^{\Delta}_n(X^0)\cong H_n(X^0)$であることは$\Delta_0(X^0)\cong C_0(X^0)$であること、$\Delta_n(X^0)=0$と$C_n(X^0)\cong C_{n-1}(X^0)$であることから従う。
$k=m-1$まで成立したとすると、Five Lemmaから任意の$k\in \mathbb{N}$について$H^{\Delta}_n(X^k)\cong H_n(X^k)$が成り立つ。
$X$が有限次元としていたから、ある$N$が存在して、$X^N$は$X$に等しい。よって帰納法の過程で$k=N$としたものが今示したかった主張を示している。
参考文献
Allen Hatcher. Algebraic Topology. Cambridge University Press , 2001.
中原幹夫. 理論物理学のための幾何学とトポロジーI(原著第2版). 日本評論社, 2018.