【図形】相加相乗平均と台形
はじめに
二つの数の平均を求める方法には、算術平均、調和平均、幾何平均などがあります。この中で算術平均は相加平均、幾何平均は相乗平均とも呼ばれ、この2つの平均には大小関係が成り立ちます。相加平均は一般に平均といわれて思い浮かべる足し算を使った平均の求め方ですね。
相加平均と相乗平均
$$ \frac{a+b}{2} $$
$$ \sqrt{ab}\ (ただしa\geq0,b\geq0) $$
相加平均と相乗平均には次のような大小関係が成り立ちます。
$$ \frac{a+b}{2}\geq\sqrt{ab}\ (ただしa\geq0,b\geq0) $$
台形に現れる相加相乗平均
図形の中で相加平均、相乗平均の値を探すことで、視覚的に相加相乗平均の大小関係を見ることができます。例えば円の中にも相加相乗平均を見つけることができます。
【図でわかる】相加相乗平均と円
台形と相加平均
台形を用いて、相加平均、相乗平均を探してみましょう。
 台形と相加平均
台形と相加平均
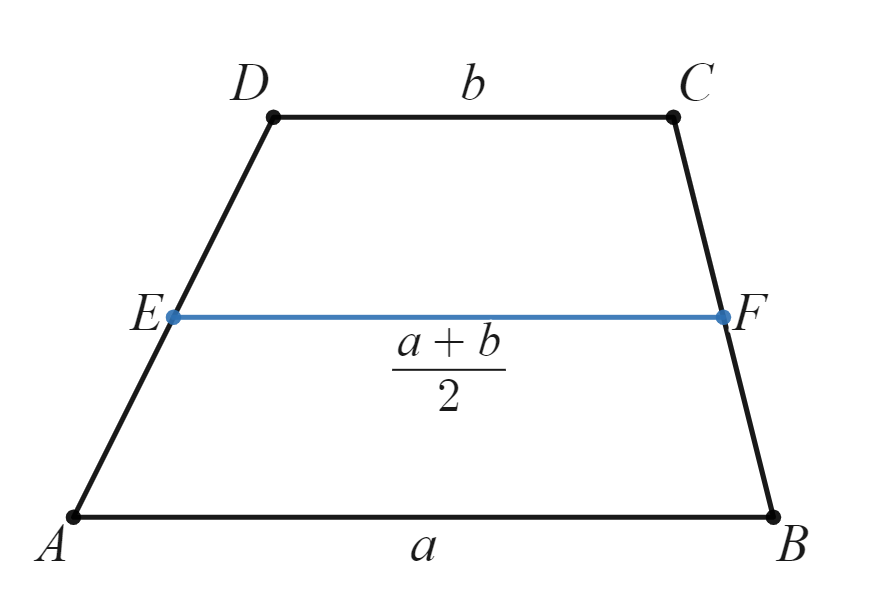
上図のような$AB/\!/DC$の台形$ABCD$を考えます。線分$AB$の長さを$a$、線分$DC$の長さを$b$とします。点$E$、点$F$をそれぞれ線分$AD$、線分$BC$の中点とすると、青い線分$EF$は$\frac{a+b}{2}$となります。実際に確認してみましょう。
 台形と相加平均
台形と相加平均
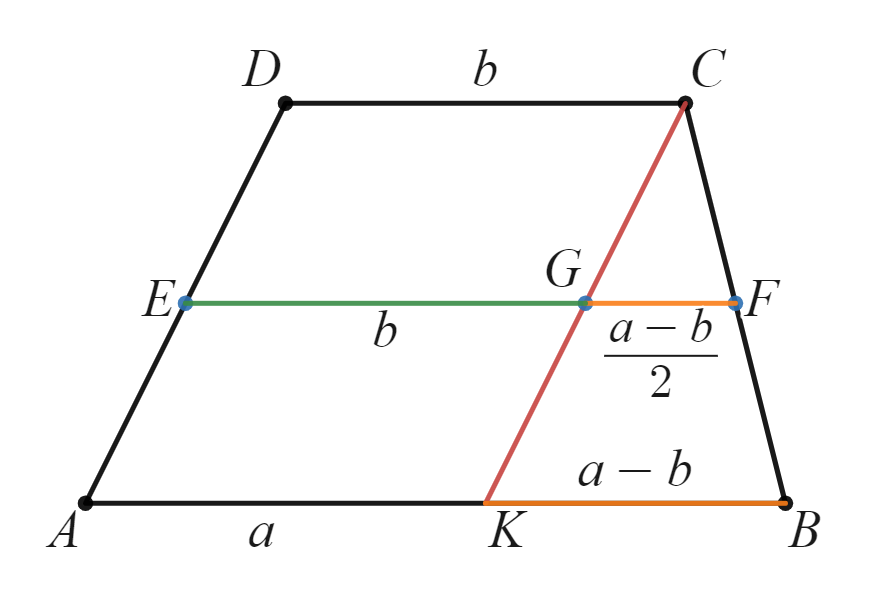
点$C$を通り線分$AD$と並行な直線と線分$AB$の交点を$K$とし、線分$CK$と線分$EF$の交点を$G$とします。すると$KB$の長さは$a-b$となります。$\triangle CKB \backsim \triangle CGF$で$CB:CF=2:1$より、$GF$の長さは$\frac{a-b}{2}$となります。一方で四角形$EGCD$は平行四辺形なので線分$EG$の長さは$b$です。なので線分$EG=EG+GF=b+ \frac{a-b}{2} =\frac{a+b}{2}$となります。
台形と相乗平均
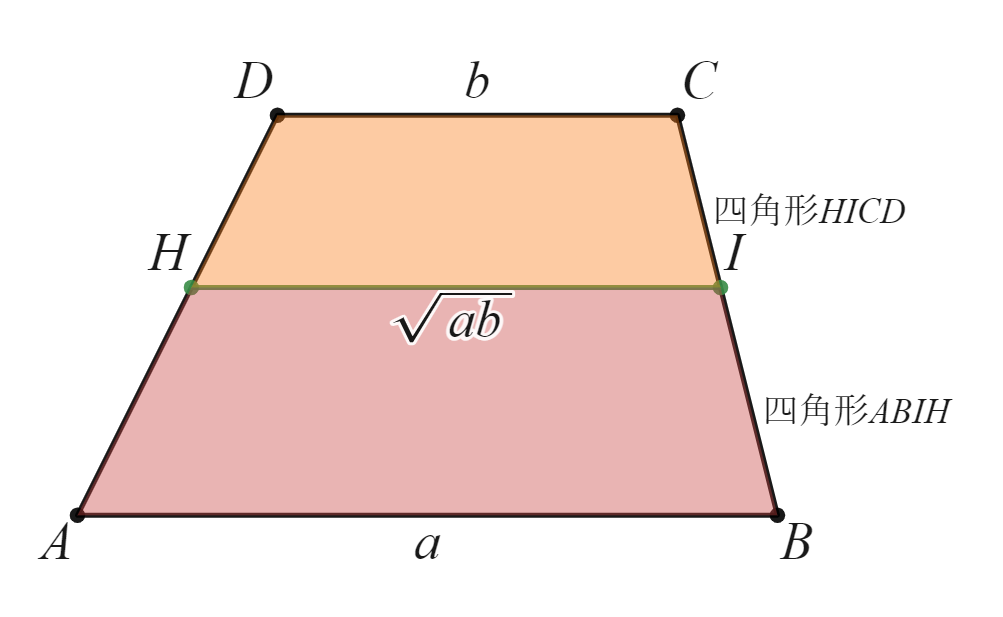
結論から書くと$四角形ABIH \backsim 四角形HICD$となるような線分$HI$の長さが$\sqrt{ab}$になります。線分$IH$の長さを$x$とおくと、$四角形ABIH \backsim 四角形HICD$より$AB:IH=IH:DC$より$a:x=x:b$なので$x^2=ab$、すなわち$x= \sqrt{ab}$となります。
 台形と相乗平均
台形と相乗平均
$四角形ABIH \backsim 四角形HICD$で$AB:HI= \sqrt{a}:\sqrt{b}$なので、台形の面積の相似比は$a:b$、高さの比は$\sqrt{a}:\sqrt{b}$となります。
まとめ
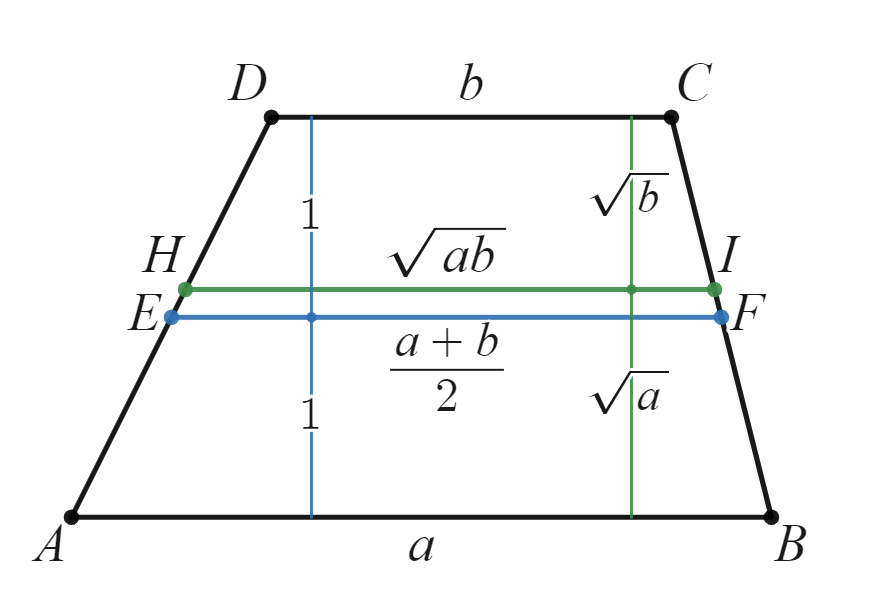
青い線分$EF$の長さが相加平均、緑の線分$HI$の長さが相乗平均です。
このように台形の中に現れる相加相乗平均を見つけることによって、大小関係を視覚的に見ることができました。
 相加相乗平均と台形
相加相乗平均と台形