太鼓を潰すと音はどのように変化するか?
通常,太鼓は円形の膜を持つことが多い.
では,太鼓の直径を変えずに円形の太鼓を細長い楕円形に潰していくと,太鼓の音はどのように変わるのだろうか?
 潰れた太鼓
潰れた太鼓
太鼓の直径を保ちながら潰すと,膜の面積が小さくなるため,太鼓の音が高くなると予想される.これは,一般に小さな太鼓は「トントン」と高い音を出すのに対し,大きな和太鼓は「ドンドン」と低い音を出すため,直感的に理解しやすい.
では,この「音が高くなる現象」を数学的に定量化できるだろうか?
太鼓の音は振動モードに対応しており,それぞれの振動モードは太鼓の膜に関連するラプラシアンのディリクレ固有値によって表される.
ラプラシアンのディリクレ固有値問題は,有界領域 $ \Omega$ に対して次のように定式化される:
$$
\begin{cases}
-\Delta u = \lambda u & \text{in } \Omega, \\
u = 0 & \text{on } \partial \Omega,
\end{cases}
$$
ここで $u$ は振動モードに対応する関数,$ \lambda$は固有値であり,
ラプラシアン$ \Delta$は次式で定義される微分作用素である:
$$
\Delta := \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}
$$
これらの固有値は,太鼓の基音や倍音に対応している.最も小さい固有値 $\lambda_1$ は基音に対応し,次の固有値 $\lambda_2, \lambda_3, \dots$ はそれぞれ2倍音,3倍音といった高次の倍音に対応する.
長方形の太鼓
楕円領域のディリクレ固有値を厳密に扱うのは困難であるため、まずは長方形領域におけるラプラシアンのディリクレ固有値問題を考える。特に、幅1、高さ$t$の長方形領域における第一固有値に注目する。
幅1, 高さ$t$ の長方形領域
幅$1$、高さ$t$の長方形領域$\Omega = [0,1] \times [0,t]$でのラプラシアンのディリクレ固有値問題は次のように定式化される:
$$
\begin{cases}
-\Delta u = \lambda u & \text{in } \Omega \\
u = 0 & \text{on } \partial \Omega
\end{cases}
$$
この問題の第一固有値(最も小さい固有値)は、次の式で与えられる:
$$
\lambda_{1,1} = \pi^2 \left( \frac{1^2}{t^2} + \frac{1^2}{1^2} \right) = \pi^2 \left( \frac{1}{t^2} + 1 \right)
$$
この式は、$t$が小さくなるにつれて固有値がどのように変化するかを捉える上で非常に重要である。
高さを潰したときの漸近挙動
領域の高さ$t$を潰していく、すなわち$t \to 0$の極限を考える。第一固有値$\lambda_{1,1}$は次のような振る舞いを示す:
$$
\lambda_{1,1} = \pi^2 \left( \frac{1}{t^2} + 1 \right)
$$
ここで$t \to 0$とすると、$\frac{1}{t^2}$の項が支配的となり、$\lambda_{1,1}$は急激に増加する。具体的には、次の漸近的な挙動が得られる:
$$
\lim_{t \to 0} t^2 \lambda_{1,1} = \pi^2
$$
この結果から、領域が潰れると第一固有値が非常に大きくなり、音が鋭く高くなることがわかる。
三角形の太鼓
 三角形の太鼓
三角形の太鼓
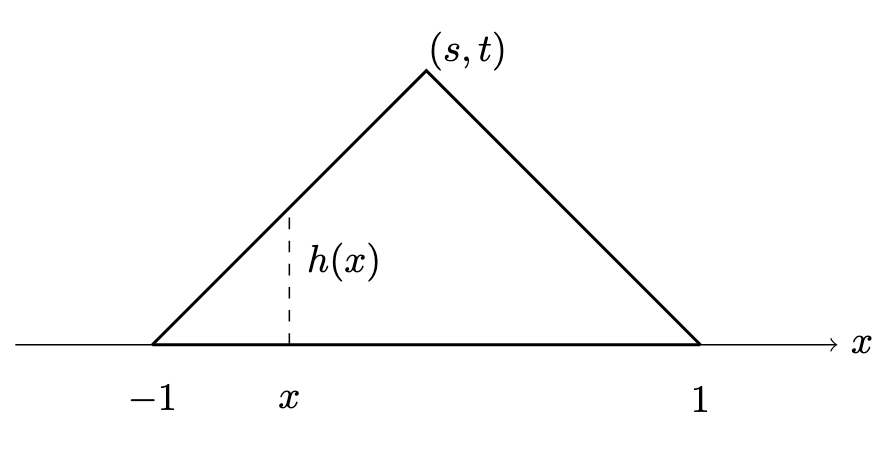
三角形領域 $T^t$ を,頂点が $(-1, 0)$,$(1, 0)$,および $(s, t)$ で定義されるものとし,その底辺は区間 $I = [-1, 1]$ であるものとする.
区間 $I$ 上で関数 $h(x)$ を次のように定義する:
$$
h(x) = \begin{cases}
\frac{t}{1+s}(x+1) & x \in [-1, s], \\
\frac{t}{1-s}(x-1) & x \in [s, 1],
\end{cases}
$$
$h(x)$は各$x$における三角形領域$T^t $の高さである.
Ourmières-Bonafos[1]は,三角形領域 $T^t$ におけるディリクレ固有値の漸近展開を次のように導いた:
$$
\lambda_k^t \sim t^{-2}\left( \pi^2 + (2\pi^2)^{2/3}\kappa_k t^{2/3} + \beta_{3,k} t + \dots \right) \quad (t \to 0),
$$
ここで,$\kappa_k$ は$\mathbb{R}$上の関数に対して定義されるシュレディンガー作用素
$$
L_s^{\text{mod}} := -\frac{d^2}{dx^2} + \left( \frac{1}{1+s}\mathbf{1}_{\mathbb{R}_-} + \frac{1}{1-s}\mathbf{1}_{\mathbb{R}_+} \right) |x|
$$
の固有値である.
漸近展開の第一項目 $ \pi^2/t^2$ が長方形の場合と同じであることは興味深い.また,第2項に現れる $(2\pi^2)^{2/3} \kappa_k t^{2/3}$ という項が加わることで,潰れる前の領域の形状が固有値に反映されていることがわかる.
Jerison の結果
(工事中)
参考文献
- Ourmières-Bonafos, Thomas. "Dirichlet eigenvalues of asymptotically flat triangles." Asymptotic Analysis 92, no. 3-4 (2015): 279-312.
