縦横の比が無理数の長方形を縦横の比が有理数のいくつかの小長方形に分割できるか？
答えはNoだ。それを主張するのが以下の定理である。
長方形$K$が縦横の比が有理数である有限個の長方形で分割されれば, $K$の縦横の比も有理数である.
この定理は一見すると明らかな命題に思える。しかし、実際の長さではなく縦横の辺の比が有理数なのであって、実際の辺の長さは無理数であってもよいことを考えるとすぐにわかることではないだろう。
準備
証明にあたり必要な数学を説明し、いくつかの命題を示す。知っている内容があれば適宜読み飛ばしたって構わない。
有向グラフ
グラフとは、頂点と辺からなる図形のことを指す。グラフの定義には様々な流儀があるが、ここでは以下のように定義する。
互いに交わらない２つの集合$V,E$の対$G=(V,E)$と, ２つの写像$i : E \to V \times V, \tau : E \to E$が次の性質を満たすとき, $G$をグラフという.
- $\tau^2 = \mathrm{id}_E$
- 各$e \in E$について, $\tau(e) \neq e$, $(i\circ\tau)(e) = (\iota \circ i)(e)$
ただし, $\iota : V \times V \to V \times V ; \iota(x,y) = (y,x)$である.
特に$V,E$がともに有限集合であるとき, $G$を有限グラフという.
辺$e$の始点を$o(e)$、終点を$t(e)$、始点と終点を逆にした辺を$\bar{e}$で表すとき、$i(e)=(o(e),t(e)), \tau(e)=\bar{e}$とすれば瞭然とした写像となる。
$G=(V,E)$をグラフとする. $E$の部分集合$E^o$で
$$
E = E^o \sqcup \bar{E}^o,\ \bar{E}^o = \{e \in E \mid \tau(e) \in E^o\} (=\{\bar{e} \mid e \in E^o\})
$$
という非交和が成り立つとき, $X^o=(V,E^o)$を（$X$の）有向グラフという. 逆に, $X$を$X^o$の向きを忘れたグラフという.
定義１の(ii)からグラフはどの辺についてもその逆向きの辺があるとも言えるが、有向グラフはそのうちのどちらか一方の向きの辺だけを選んで向きを定めることだと言える。
グラフ$G=(V,E)$について, 任意の異なる2点$x,y \in V$に対して, ある頂点の列$\{v_k\}_{k=0}^n \subset V$と辺の列$\{e_k\}_{k=1}^n \subset E$があって
$$
x=v_0,\ y=v_n,\ i(e_k) = (v_{k-1},v_k) \enspace (k=1,\cdots,n)
$$
となるとき, $G$は連結であるという.
このような頂点列を道ということもある。要するに、任意の異なる２つの頂点の間に道がある（辺を渡ってたどり着ける）ときに連結である。
グラフ$X=(V,E)$について, 関数$m_V:V\to\mathbb{R},\ m_E:E\to\mathbb{R}$が
$$
m_V(v)>0 \enspace (v \in V), \quad m_E(e)=m_E(\bar{e})>0 \enspace (e \in E)
$$
を満たすとき, $m_V,m_E$をそれぞれ頂点, 辺の重み関数という.
また, $m_V(v)$を頂点$v$の重み, $m_E(e)$を辺$e$の重みという.
重み関数$m_V,m_E$が与えられたグラフを重み付きグラフという.
離散ラプラシアンのポアソン方程式
ラプラシアンといえば、三変数関数$f(x,y,z)$なら
$$
\Delta f \coloneqq \frac{ \partial^2 f }{ \partial x^2 } + \frac{ \partial^2 f }{\ \partial y^2} + \frac{ \partial^2 f }{\partial z^2}
$$
のことを指すだろう。また、このラプラシアン関する
$$
\Delta f = g \quad (D\,\text{上})
$$
という二階偏微分方程式はポアソン方程式と呼ばれる。
これが解をもつための必要十分条件は（適当な条件下で）
$$
\iiint_{D} g(x,y,z) \ dx\,dy\,dz = 0
$$
であることが知られており、解は定数差を除き一意的であることも確かめられる。
ここでは重み付きグラフに対して定義される離散的なラプラシアンとそのポアソン方程式を考える。以後、$X=(V,E)$を$m_V,m_E$を重み関数とする重み付き有限連結グラフとする。
$E_v \coloneqq \{e \in E \mid o(e)=v\},\ C^o(X)\coloneqq \{f : V \to \mathbb{R}\}$とする.
このとき$C^0(X)$は通常の和とスカラー倍で$\mathbb{R}$上線形空間である.
線形写像$\Delta : C^0(X) \to C^0(X)$を
$$
(\Delta f)(v) \coloneqq \frac{1}{m_V(v)} \sum_{e\in E_v} m_E(e)\{f(t(e))-f(o(e))\}
$$
で定めるとき, $\Delta$を離散ラプラシアンという.
なぜこれがラプラシアンの名を冠すかについては参考文献に述べられているので、そちらを参照されたい。なお、$C^0(X)$の$0$は関数の始域である頂点の次元である。
$g \in C^0(X)$を与えたとき, 未知関数$f \in C^0(X)$に関する次の方程式について(1),(2)が成り立つ.
$$
\Delta f = g \qquad \text{（離散的ポアソン方程式）}
$$
- 解が存在すれば, 定数差を除いて一意に定まる.
- 解が存在するための必要十分条件は以下である.
$$ \sum_{v \in V} g(v) m_V(v) = 0 $$
通常のポアソン方程式で成り立つことと同様のものである。
この定理の証明に用いる補題を先に示す。
$C^1(X)\coloneqq\{\omega : E \to \mathbb{R} \mid {}^\forall e \in E,\ \omega(\bar{e}) = -\omega(e)\}$とする.
これは$C^0(X)$と同様の演算で$\mathbb{R}$上線形空間である.
線形写像$d : C^0(X) \to C^1(X)$を
$$
(df)(e) \coloneqq f(t(e))-f(o(e))
$$
で定めるとき, $df \equiv 0$ならば$f$は定数関数である.
なお、この補題の逆は明らかに成り立つ。
$df \equiv 0$ならば任意の辺$e \in E$に対し$f(t(e))=f(o(e))$である.
つまり, 隣り合う２つの頂点での$f$の値は等しい.
$X$は連結であったから, $f$は定数関数である. $\fbox{}$
線形空間$C^0(X),C^1(X)$に内積$\iprod{\cdot}{\cdot}_0,\iprod{\cdot}{\cdot}_1$を以下で定義する.
\begin{align}
\iprod{f}{g}_0 &\coloneqq \sum_{v \in V} f(v)g(v)m_V(v) \quad (f,g \in C^0(X)) \\
\iprod{\omega}{\eta}_1 &\coloneqq \frac{1}{2}\sum_{e \in E} \omega(e)\eta(e)m_E(e) \quad (\omega,\eta \in C^1(X))
\end{align}
このとき, $\varphi,\psi \in C^0(X)$に対して以下が成り立つ.
$$
\iprod{\varphi}{\Delta\psi}_0 = -\iprod{d\varphi}{d\psi}_1
$$
$\iprod{\cdot}{\cdot}_1$に係数$\frac{1}{2}$があるのは、$\omega(e)\eta(e)m_E(e)=\omega(\bar{e})\eta(\bar{e})m_E(\bar{e})$となるからである。それぞれが内積となっているかの確認は読者に委ねる。
\begin{align} \iprod{\varphi}{\Delta\psi}_0 &= \sum_{v \in V} \varphi(v)(\Delta\psi)(v)m_V(v) \\ &= \sum_{v \in V} \varphi(v) \left( \sum_{e\in E_v} m_E(e)\{\psi(t(e))-\psi(o(e))\} \right) \\ &= \sum_{v \in V} \sum_{e \in E_v} \varphi(o(e))\{\psi(t(e))-\psi(o(e))\}m_E(e) \\ &= \sum_{e \in E} \varphi(o(e))\{\psi(t(e))-\psi(o(e))\}m_E(e) \\ & \left(\begin{split} & \sum_{e \in E} \varphi(o(e))\{\psi(t(e))-\psi(o(e))\}m_E(e) \\ =& \sum_{e \in E} \varphi(o(\bar{e}))\{\psi(t(\bar{e}))-\psi(o(\bar{e}))\}m_E(\bar{e}) \\ =& \sum_{e \in E} \varphi(t(e))\{\psi(o(e))-\psi(t(e))\}m_E(e) \\ =& -\sum_{e \in E} \varphi(t(e))\{\psi(t(e))-\psi(o(e))\}m_E(e) \end{split}\right) \\ &=\ \begin{split} \frac{1}{2}\Biggl(&\sum_{e \in E} \varphi(o(e))\{\psi(t(e))-\psi(o(e))\}m_E(e) \\ &- \sum_{e \in E} \varphi(t(e))\{\psi(t(e))-\psi(o(e))\}m_E(e) \Biggr) \end{split} \\ &= \frac{1}{2}\sum_{e \in E} \{\varphi(o(e))-\varphi(t(e))\}\{\psi(t(e))-\psi(o(e))\}m_E(e) \\ &= -\frac{1}{2}\sum_{e \in E} \{\varphi(t(e))-\varphi(o(e))\}\{\psi(t(e))-\psi(o(e))\}m_E(e) \\ &= -\frac{1}{2}\sum_{e \in E} (d\varphi)(e)(d\psi)(e)m_E(e) \\ &= -\iprod{d\varphi}{d\psi}_1 \enspace \fbox{} \end{align}
では、これらの補題から定理２を証明する。
(1) 解が存在すれば, 定数差を除いて一意に定まる.
$f_1,f_2$がともに解であるとし, $f = f_1-f_2$とする.
$f$が定数関数であることを示せばよい.
$$
\Delta f = \Delta f_1 - \Delta f_2 = g - g = 0
$$
である. よって, 補題４より
$$
\iprod{df}{df}_1 = -\iprod{f}{\Delta f}_0 = 0
$$
であるので$df = 0$で, 補題３より$f$は定数関数である. $\fbox{}$
(2) 解が存在するための必要十分条件は以下である.
$$
\sum_{v \in V} g(v) m_V(v) = 0
$$
補題４で, $\varphi\equiv1,\psi = f$とすれば
$$
\sum_{v \in V} (\Delta f)(x)m_V(v) = \iprod{1}{\Delta f}_0 = -\iprod{d1}{df}_1 = -\iprod{0}{df} = 0
$$
となる. よって, $\Delta f = g$の解$f$が存在するならば
$$
\sum_{v \in V} g(v)m_V(v) = 0
$$
である. つまり, 線形写像$S:C^0(X)\to\mathbb{R}$を
$$
S(g) \coloneqq \sum_{v \in V} g(v)m_V(v)
$$
で定めると, $\Im \Delta \subseteq \Ker S$は部分空間である.（等号成立を示す.）
また, $\Delta,S$についての次元定理より
\begin{align}
\dim(C^0(X)) &= \dim(\Ker\Delta)+\dim(\Im\Delta) \\
\dim(C^0(X)) &= \dim(\Ker S)+\dim(\Im S) \\
\end{align}
であるが, このとき$\dim(\Ker\Delta) = \dim(\Im S) = \dim(\mathbb{R}) = 1$である.
（実際, (1)より$\Delta f = 0$となる$f \in C^0(X)$は定数関数に限られるので$\Ker\Delta$は定数関数からなる空間なので$\mathbb{R}$と見なせるし, 任意の実数$y$に対して$g \equiv y\left(\sum_{v \in V} m_V(v)\right)^{-1} \in C^0(X)$とすれば$y=S(g)$となるから$S$は全射である.）
したがって, $\dim(\Im\Delta) = \dim(\Ker S)$であるから
$$
\Im\Delta = \Ker S \enspace \fbox{}
$$
次に、定理１の証明に直接つながる命題を示す。
有理数値関数で重み付けられたグラフについて, $g$を有理数値関数としたときの離散的ポアソン方程式の解が存在するなら, 有理数値関数の解も存在する.
$C^0(X,\mathbb{Q}) \coloneqq \{f:V\to\mathbb{Q}\}$は$\mathbb{Q}$上線形空間である.
また, $\Delta$の定義から$f \in C^0(X,\mathbb{Q})$なら$\Delta f \in C^0(X,\mathbb{Q})$である.
よって, $\Delta$の$C^0(X,\mathbb{Q})$への制限
$$
\Delta^\mathbb{Q} : C^0(X,\mathbb{Q}) \to C^0(X,\mathbb{Q})
$$
は$\mathbb{Q}$上の線形写像となる. 同様にして$S$の$C^0(X,\mathbb{Q})$への制限
$$
S^\mathbb{Q} : C^0(X,\mathbb{Q}) \to \mathbb{Q}
$$
も$\mathbb{Q}$上の線形写像となる. 補題４より$S\circ\Delta \equiv 0$であったから
$$
S^\mathbb{Q}\circ\Delta^\mathbb{Q} \equiv 0
$$
は当然成り立つ. つまり$\Im\Delta^\mathbb{Q}\subset\Ker S^\mathbb{Q}$である.
よって, 定理２の証明において$C^0(X)$を$C^0(X,\mathbb{Q})$に, $\mathbb{R}$を$\mathbb{Q}$に置き換えることで$\Im\Delta^\mathbb{Q}=\ker S^\mathbb{Q}$が同様に示せる.
したがって$g \in \Ker S \cap C^0(X,\mathbb{Q}) = \Ker S^\mathbb{Q} = \Im\Delta^{\mathbb{Q}}$であるので
$$
\Delta f_\mathbb{Q} = \Delta^\mathbb{Q} f_\mathbb{Q} = g
$$
となる解$f_\mathbb{Q} \in C^0(X,\mathbb{Q})$が存在する. $\fbox{}$
定理５の状況で, $f$が解ならば任意の頂点$x,y$に対し
$$
f(y)-f(x) \in \mathbb{Q}
$$
定理５より, $\Delta f = g$が解$f$をもてば有理数値関数の解$f_\mathbb{Q}$がある.
このとき, 定理２の(1)から$f-f_\mathbb{Q}$は定数関数であるので
$$
f(y)-f(y)_\mathbb{Q} = f(x)-f_\mathbb{Q}(x)
$$
したがって$f(y)-f(x) = f_\mathbb{Q}(y)-f_\mathbb{Q}(x) \in \mathbb{Q} \enspace \fbox{}$
長方形分割のデーンの定理
いざ、証明しよう。準備が長くなったので再掲する。
与えられた長方形$K$が, 縦横の比が有理数である有限個の長方形で分割されれば, $K$の縦横の比も有理数である.
先に証明のプロセスを紹介する。
- 長方形分割に対応する有向グラフを考える
- 有理数値関数での上手い重み付けと関数を与える
- それを解とする離散的ポアソン方程式を見つける
- 定理５の系から結論が従う
相似な長方形を考えることにより, $K$の縦の長さを$1$と仮定すれば横の長さが有理数となることを示せば十分であるとわかる. これを示す.
まず, 長方形分割に対応する有向グラフを考える.
$K$の長方形分割に現れる, $K$の縦の辺に平行な線分（以降, 縦線分という）を要素とする集合を頂点集合$V$とし, 各小長方形を要素とする集合を有向辺集合$E^o$とする. ここで各$e \in E^o$に対し$o(e),t(e)$をそれぞれ$e$に対応する小長方形の左側, 右側を含む縦線分とする.
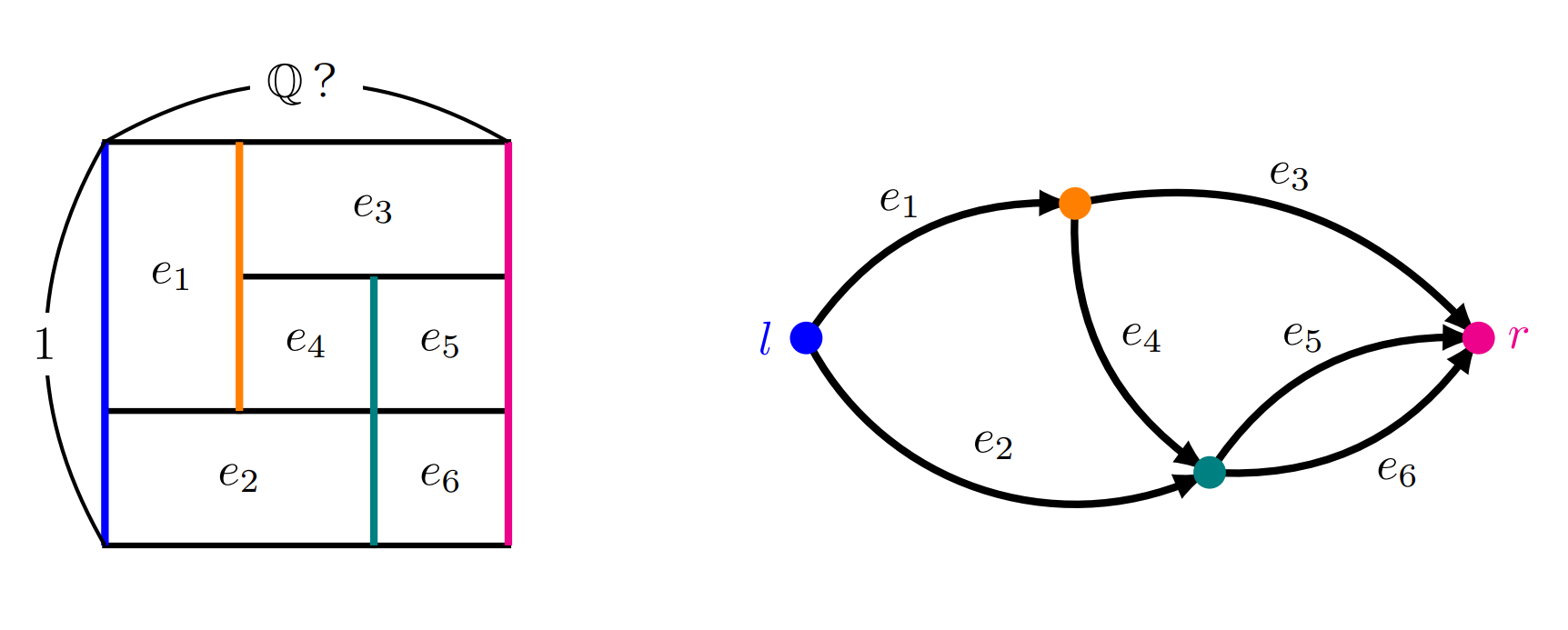長方形分割と対応する有向グラフの例
こうして得られる有向グラフ$X^o=(V,E^o)$に対して, その向きを忘れたグラフを$X=(V,E)$とする. これらは有限グラフである.
また, $K$の左側, 右側の辺に対応する頂点をそれぞれ$\textcolor{blue}{l},\textcolor{magenta}{r}$とする.
このとき, 任意の頂点$v \in V$に対して$v \neq r$なら$o(e)=v$となる辺$e \in E^o \subset E$が存在する. $\cdots(\star)$
$X$の有限性より, $v_n=r$となるまで$(\star)$を繰り返せば$(v_{k-1},v_k)\in E$であるような頂点の列$\{v=v_0,\cdots,v_n=r\}$を取ることができて, これは$v$から$r$への道である. よって, 任意の異なる2点の間には少なくとも$r$が媒介する道があるので$X$は連結である.
次に, $X$の重み関数を定義する.
$$
m_V \equiv 1 \qquad m_E(e) \coloneqq \frac{\text{小長方形 }e \text{ の縦の長さ}}{\text{小長方形 } e \text{ の横の長さ}} \enspace (e \in E)
$$
とすると$m_V$は明らかに, $m_E$は仮定より有理数値関数である.
また, $f \in C^0(X)$を
$$
f(v) \coloneqq \text{辺 } l \text{ から縦線分 } v \in V \text{までの距離} \enspace (v \in V)
$$
で定めると, 任意の小長方形$e \in E^o \subset E$に対して
$$
f(t(e))-f(o(e)) = e \text{ の横の長さ}
$$
となる. よって
$$
m_E(e) \{f(t(e))-f(o(e))\} = e \text{ の縦の長さ}
$$
であり, 各縦線分$v \in V$に対して
\begin{align}
\sum_{e \in E^0,\ o(e)=v} m_E(e) \{f(t(e))-f(o(e))\} &= \text{縦線分 } v \text{ の長さ} \enspace (v \neq r) \\
\sum_{e \in E^0,\ t(e)=v} m_E(e) \{f(t(e))-f(o(e))\} &= \text{縦線分 } v \text{ の長さ} \enspace (v \neq l)
\end{align}
が得られる.
以上から$\Delta f$について考える. $v \in V$について
(i) $v \neq l$かつ$v \neq r$のとき
\begin{align}
(\Delta f) (v) &= \sum_{e \in E_v} m_E(e)\{f(t(e))-f(o(e))\} \\
&= \sum_{e \in E^o,\ o(e)=v} m_E(e)\{f(t(e))-f(o(e))\} + \sum_{e \in \bar{E}^o,\ o(e)=v} m_E(e)\{f(t(e))-f(o(e))\} \\
&= \sum_{e \in E^o,\ o(e)=v} m_E(e)\{f(t(e))-f(o(e))\} + \sum_{e \in E^o,\ o(\bar{e})=v} m_E(\bar{e})\{f(t(\bar{e}))-f(o(\bar{e}))\} \\
&= \sum_{e \in E^o,\ o(e)=v} m_E(e)\{f(t(e))-f(o(e))\} - \sum_{e \in E^o,\ o(e)=v} m_E(e)\{f(t(e))-f(o(e))\} \\
&= 0
\end{align}
(ii) $v=l$のとき
$t(e)=l$となる$e \in E^0$は存在しない.
よって$E_l = \{e \in E \mid o(e) = l\} = \{e \in E^o \mid o(e) = l\}$であるから
\begin{align}
(\Delta f)(l) &= \sum_{e \in E_l} m_E(e)\{f(t(e))-f(o(e))\} \\
&= \sum_{e \in E^0,\ o(e)=l} m_E(e)\{f(t(e))-f(o(e))\} \\
&= \text{辺 } l \text{ の長さ} = 1
\end{align}
(iii) $v=r$のとき
$o(e)=r$となる$e \in E^0$は存在しない.
よって$E_r = \{e \in E \mid o(e) = r\} = \{e \in E^o \mid t(e) = r\}$であるから
\begin{align}
(\Delta f)(r) &= \sum_{e \in E_r} m_E(e)\{f(t(e))-f(o(e))\} \\
&= -\sum_{e \in E^0,\ t(e)=r} m_E(e)\{f(t(e))-f(o(e))\} \\
&= -(\text{辺 } r \text{ の長さ}) = -1
\end{align}
以上, (i),(ii),(iii)より$g \in C^0(X)$を
$$
g(v) \coloneqq \left\{\begin{array}{cl}
0 & (v \neq l,r) \\
1 & (v = l) \\
-1 & (v=r)
\end{array}\right.
$$
とおけば, $f$は離散的ポアソン方程式
$$
\Delta f = g
$$
の解である.
したがって, $X$は有限連結グラフであって$m_V,m_E,g$は有理数値関数であるから, 定理５の系より
$$
f(l)-f(r) = K\text{ の横の長さ} \in \mathbb{Q} \quad \fbox{}
$$
おわりに
この定理を知ったきっかけは私の高校時代の友人がふと送信してきたメッセージであった。「縦横の比が無理数である長方形を、縦横の比が有理数の長方形を有限個使って敷き詰められるか」という、まさにこの定理が答えとなる問いそのものであった。周りの数学徒と幾度か議論を交わし、その中で得た面白い結果もあった。実際の証明にもあるグラフを与えてみるというアイデアも考え付いたが、証明には届かなかった。
最終的には、すでに証明されているらしいと聞いてこの定理を知った。証明自体は難しいものではないが、数学の分野を横断した非常に学びの多いものであった。実は数学だけでなく、物理の電気回路で用いられる考え方（離散的ラプラシアン）も関連しているということには驚いた。
参考文献には、この定理の証明や電気回路との関連、さらにはもう１つの（多面体の分割に関する）デーンの定理の証明なども述べられている。これらの内容にご関心のある方は、ぜひご一読いただきたい。
主張は直観的で理解しやすいが、証明には確かな数学が必要になる。そのような定理には、特段の美しさがある。
