テンソル積と直和は交換する
加群のテンソル積が直和と交換するという命題を証明します．まずテンソル積の定義を確認します．
$A$を環とする．
$X$を右$A$加群，$Y$を左$A$加群，$M$をAbel群とする．$\phi\colon X\times Y\to M$が次を充たすとき，$\phi$は$A$平衡であるという．任意の$x,x'\in X,y,y'\in Y,a\in A$に対し，
- $\phi(x+x',y)=\phi(x,y)+\phi(x',y)$
- $\phi(x,y+y')=\phi(x,y)+\phi(x,y')$
- $\phi(xa,y)=\phi(x,ay)$
$X\times Y$から$M$への$A$平衡全体を$\Bal_A(X,Y;M)$で表す．
$X$を右$A$加群，$Y$を左$A$加群とする．組$(T,\phi)$が次の(1),(2)を充たすとき，$(T,\phi)$または$T$を$X,Y$のテンソル積，$\phi$をテンソル積の構造射と云う．
- $T$はAbel群，$\phi\in \Bal_A(X,Y;T)$
- $(S,\psi)$も(1)を充たすとき，(つまり$S$はAbel群，$\psi\in\Bal_A(X,Y;S)$のとき)
$$\ex! f\in\Hom_{\Ab}(T,S),\psi=f\circ\phi$$
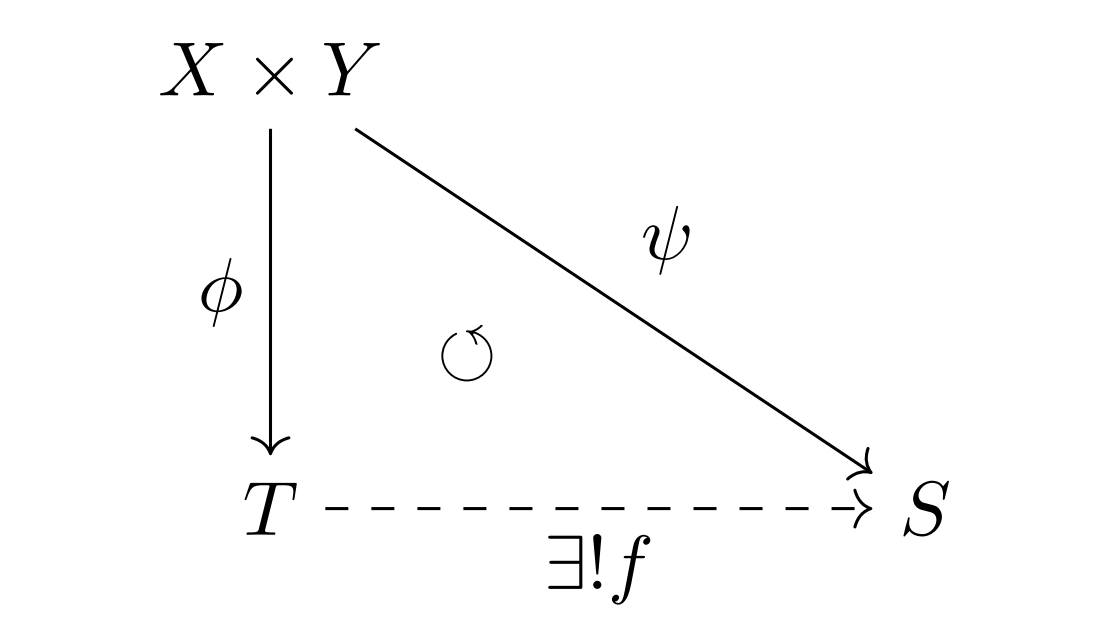テンソル積の普遍性
テンソル積はuniqueに存在して$\dps T=X\otimes_A Y$で表す．
条件(1)(2)をテンソル積の普遍性という．
$\phi(x,y)$を$x\otimes_A y$とかく．また$\phi$を$\otimes_A$とかく．
次に直和の定義を確認します．この定義において$A$加群とは左$A$加群または右$A$加群のどちらかとします．
$\{X_\lam\}_{\lam\in\Lam}$を$A$加群族とする．組$(X,\{\iota_\lam\}_{\lam\in\Lam})$が次の(1),(2)を充たすとき，$(X,\{\iota_\lam\}_{\lam\in\Lam})$または$X$を$\{X_\lam\}_{\lam\in\Lam}$の直和，$\iota_\lam$を包含という．
- $X$は$A$加群，$\all \lam\in\Lam,\iota_\lam\in\Hom_A(X_\lam,X)$
- $(M,\{j_\lam\}_{\lam\in\Lam})$が(1)を充たすとき，
$$\ex!\Phi\in\Hom_A(X,M),\all\lam\in\Lam,j_\lam=\Phi\circ \iota_\lam$$
を充たすことを云う．直和はuniqueに存在して$\dps X=\bigoplus_{\lam\in\Lam}X_\lam$と表す．
今回示す定理です．
右$A$加群族$\{X_{\lam}\}_{\lam\in\Lam}$と左$A$加群族$\{Y_{\mu}\}_{\mu\in M}$に対して，
$$\br{\bigoplus_{\lam\in\Lam} X_{\lam}}\otimes_A \br{\bigoplus_{\mu\in M} Y_{\mu}}\cong \bigoplus_{(\lam,\mu)\in\Lam\times M}\br{X_{\lam}\otimes_A Y_\mu}$$
$$\iota_{\lam}\colon X_\lam\to\bigoplus_{\lam\in\Lam}X_\lam$$
$$\iota_{\mu}:Y_\mu\to\bigoplus_{\mu\in M}Y_\mu$$
$$\iota_{(\lam,\mu)}\colon X_{\lam}\otimes_A Y_\mu\to\bigoplus_{(\lam,\mu)\in\Lam\times M}\br{X_{\lam}\otimes_A Y_\mu}$$
を包含とする．直和$\bigoplus_{(\lam,\mu)\in\Lam\times M}\br{X_{\lam}\otimes_A Y_\mu}$の普遍性よりAbel群準同型$f$が存在して，任意の$(\lam,\mu)$に対し次を可換にする．
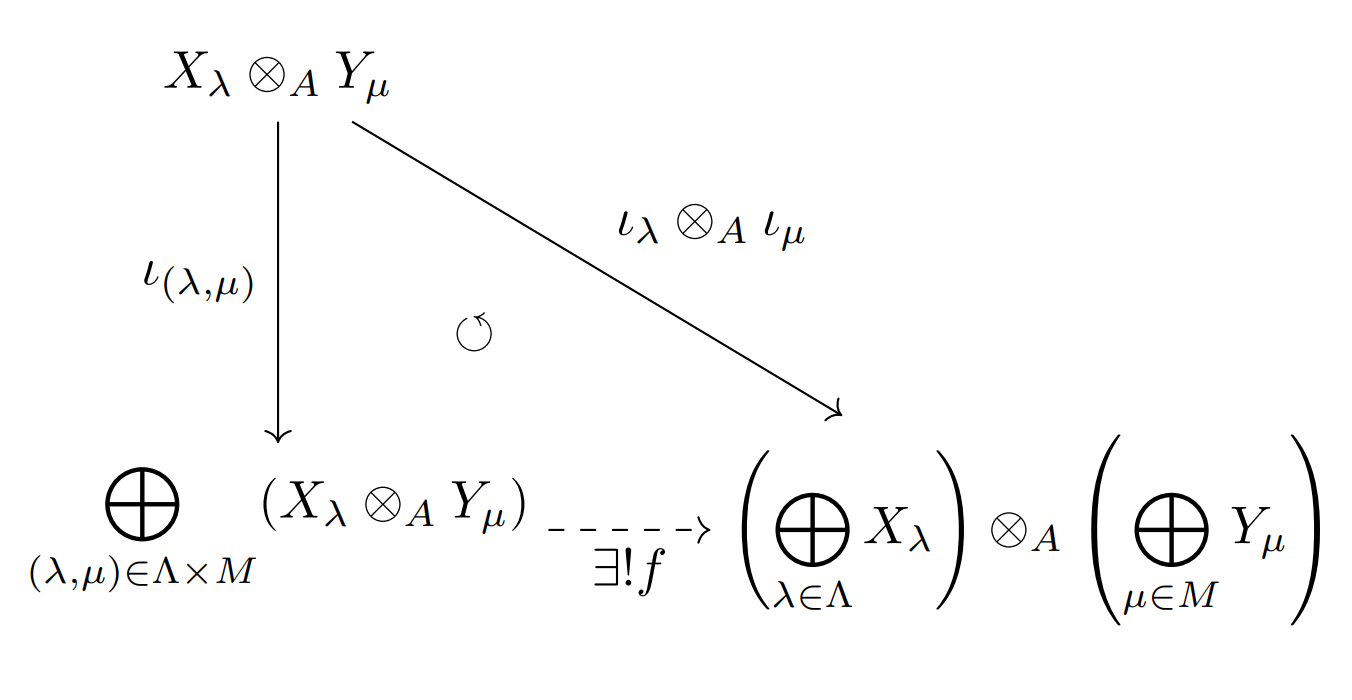直和の普遍性
但し，$\iota_\lam\otimes_A\iota_\mu$は$A$加群の準同型のテンソル積である．
一方，
\begin{align}
\psi\colon\br{\bigoplus_{\lam\in\Lam} X_{\lam}}\times\br{\bigoplus_{\mu\in M} Y_{\mu}}&\to\bigoplus_{(\lam,\mu)\in\Lam\times M}\br{X_{\lam}\otimes_A Y_\mu}\\
((x_\lam)_{\lam},(y_\mu)_\mu)&\mapsto (x_\lam\otimes y_\mu)_{(\lam,\mu)}
\end{align}
と定めると，これは$A$平衡なので，テンソル積$\br{\bigoplus_{\lam\in\Lam} X_{\lam}}\otimes_A \br{\bigoplus_{\mu\in M} Y_{\mu}}$の普遍性によりAbel群準同型$g$が存在して，次を可換にする．
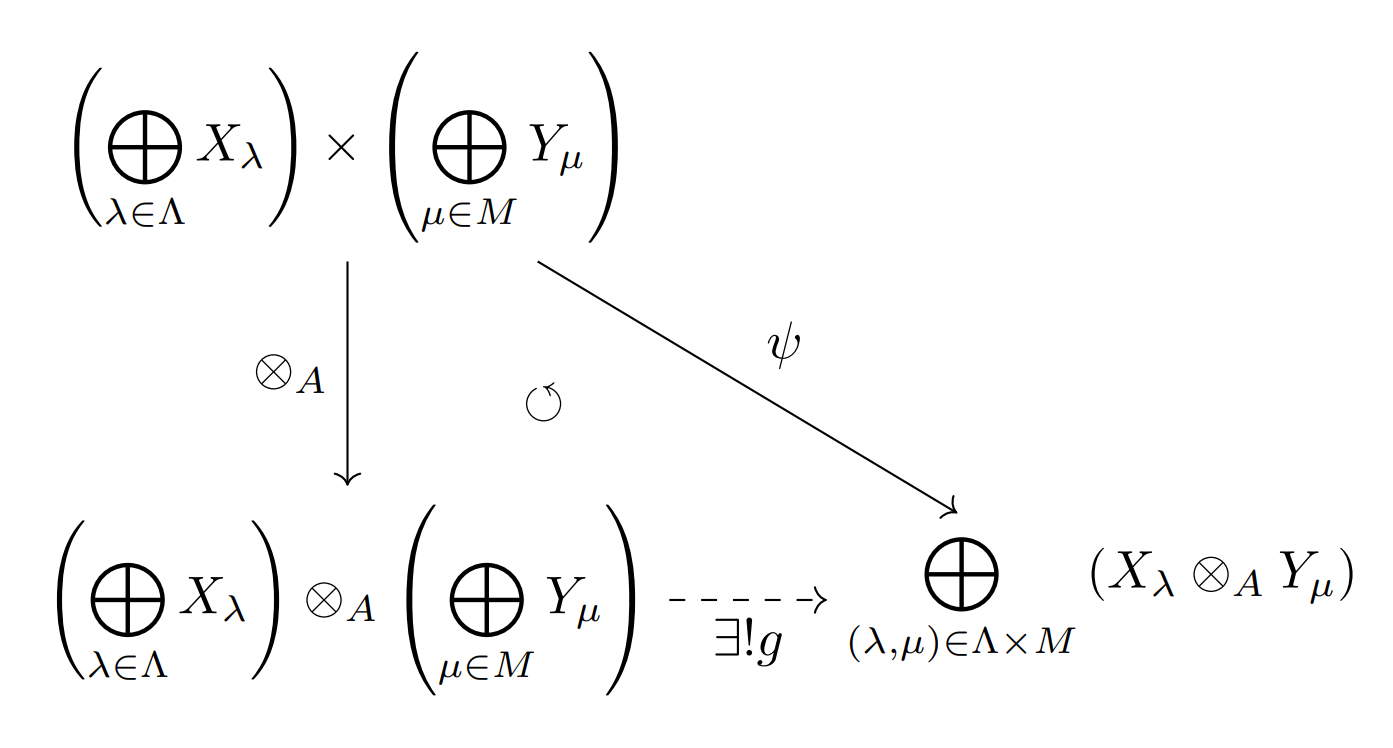テンソル積の普遍性
見づらいのでここから$\otimes_A$を$\otimes$とかく．
$$f(\iota_{(\lam,\mu)}(x\otimes y))=\iota_\lam(x)\otimes\iota_\mu(y)$$
$$g((x_\lam)_\lam\otimes (y_\mu)_\mu)=(x_\lam\otimes y_\mu)_{(\lam,\mu)}$$
に注意すると，
\begin{align} g\circ f(\iota_{(\lam,\mu)}(x\otimes y)) &=g(\iota_\lam(x)\otimes\iota_\mu(y))\\ &=\iota_{(\lam,\mu)}(x\otimes y) \end{align}
\begin{align}
f\circ g((x_\lam)_\lam\otimes (y_\mu)_\mu)
&=f((x_\lam\otimes y_\mu)_{(\lam,\mu)})\\
&=f\br{\sum_{(\lam,\mu)}\iota_{(\lam,\mu)}(x_\lam\otimes y_\mu)}\\
&=\sum_{(\lam,\mu)}f(\iota_{(\lam,\mu)}(x_\lam\otimes y_\mu))\\
&=\sum_{(\lam,\mu)}\iota_\lam(x_\lam)\otimes\iota_\mu(y_\mu)\\
&=(x_\lam)_\lam\otimes (y_\mu)_\mu
\end{align}
である．生成元での等式を線型に拡張することで
$$g\circ f=\id,\;f\circ g=\id$$
を得る．よって$f$は同型である．
$$f\colon\br{\bigoplus_{\lam\in\Lam} X_{\lam}}\otimes_A \br{\bigoplus_{\mu\in M} Y_{\mu}}\cong \bigoplus_{(\lam,\mu)\in\Lam\times M}\br{X_{\lam}\otimes_A Y_\mu}$$
テンソル積と直和の普遍性を用いて示すことができました．
