Penrose diagram

皆さん初めまして！
東京大学教養学部統合自然科学科B3のRelLimです。
今回は駒場理数サークルAdvent Calendar 2日目として、Penrose diagramについて扱っていきます。

　世界地図は、丸い地球を平面の紙に無理なく収めるために、メルカトル図法などの様々な工夫が凝らされています。では、もし「宇宙全史」ー宇宙の始まりから終わりまで、そしてその果てしない広がりを1枚の紙に描くとしたら、どうすればいいでしょうか？
　これを可能にするのが、物理学者Roger Penroseが考案したPenrose diagramです。この図は、時間と空間を巧みに縮めることで、無限の宇宙を有限の領域に描き出します。無限の時間を超え、光すら脱出できないブラックホールの先まで、宇宙全体の構造を直感的に理解することができるようになります。

　この記事の目標は次のPenrose diagramを理解できるようになることです。
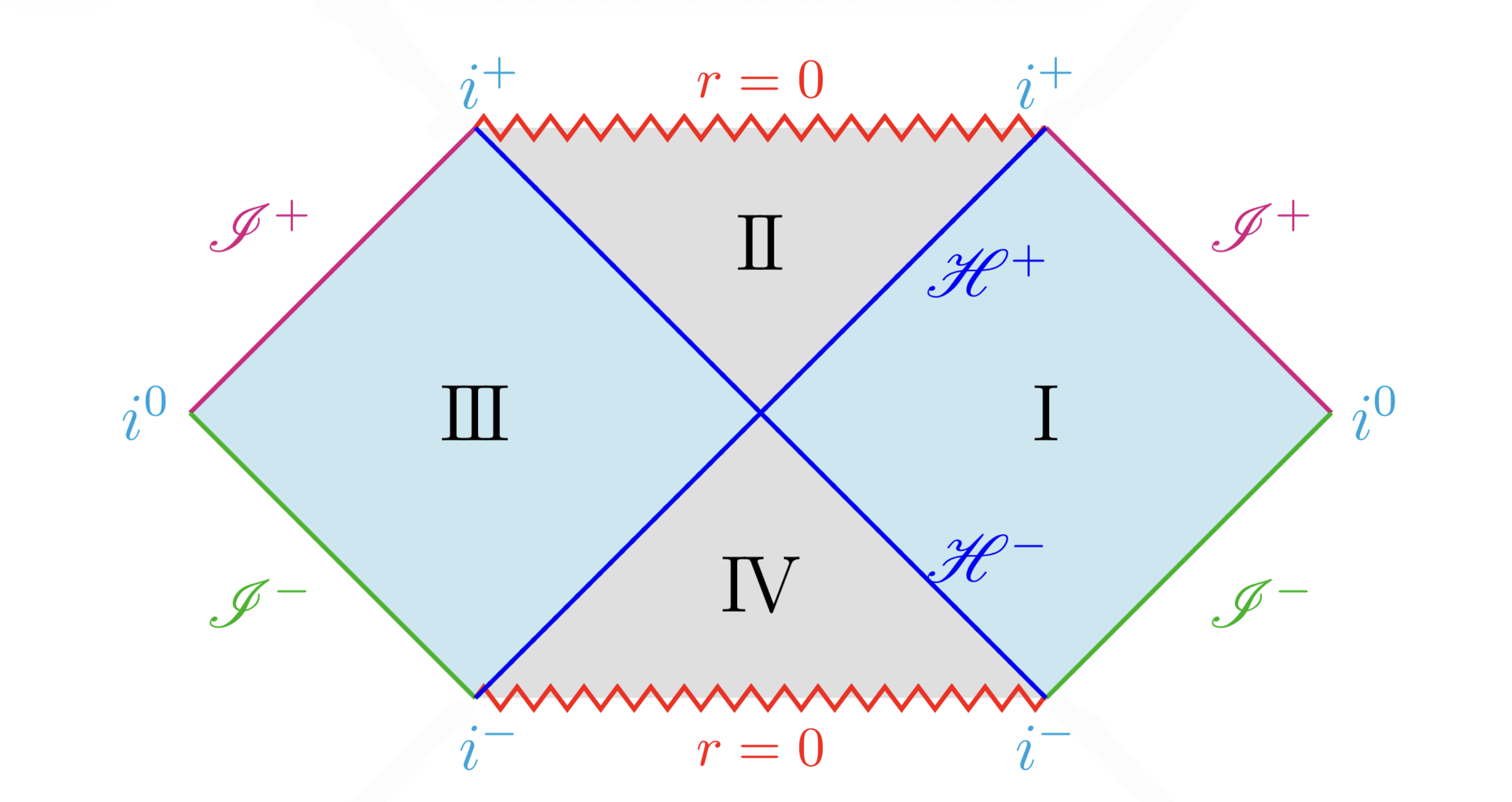Penrose diagram
　実はこの図、中心にブラックホールをもつ宇宙全体を表した図になっています。Ⅰと書かれた領域が、私たちが今住んでいる宇宙に対応し、Ⅱと書かれた領域がブラックホールを表しています。

　この図について紐解いていくために、まずはブラックホール、ひいては重力を物理的に記述するための準備である一般相対性理論について解説します。その後、まずは分かりやすい宇宙を考えることでPenrose diagramの描き方を解説し、これらの準備の下で、ブラックホールを描いたPenrose diagramに挑みます。

1. 一般相対性理論

　Penrose diagramが描けるようになるには、まずは時空を記述する物理である一般相対性理論を理解する必要があります。しかしながら、これは非常に難しい理論であるため、今回は必要な知識を紹介するにとどめようと思います。

1.1 一般相対性理論の指導原理

　一般相対性理論は、次の2つの原理から導かれています

　このふたつの原理から自然と導かれる理論が一般相対性理論です。これらの原理について少し述べておきます。

等価原理

　宇宙空間にエレベーターの箱を置き、その中に人を乗せて地球へ向かって自由落下させる状況を考えます。
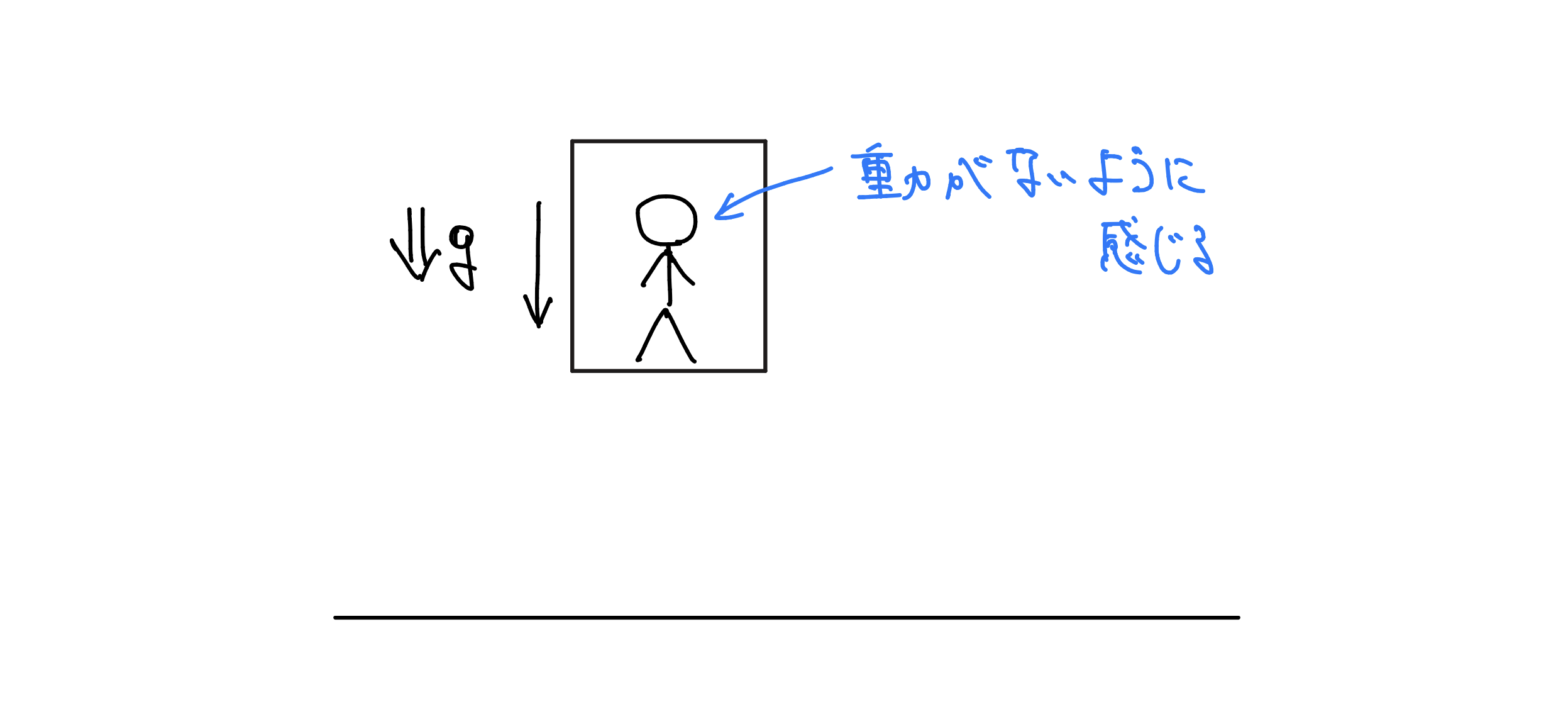自由落下するエレベーターの箱とその中の人

　エレベーターの箱は地球における重力加速度$g$で自由落下します。しかし、エレベーターの中の人は、自分が静止しているように感じます。これは、中の人の座標系が自由落下しているためです。
　このように、重力は局所的には座標変換によって打ち消すことができます。局所的に打ち消すことが出来るのは、重力質量$m_g$と慣性質量$m_i$の差が非常に小さいことに起因しています。重力質量とは、物体がどれほど重力を受けるかの時空の物理量であり、慣性質量はその物体がどれほど動きづらいかを表す物質の物理量になります。自由落下する物体の運動方程式を、重力質量と慣性質量を用いて表すと次式のようになります。

\begin{align} m_i\frac{\mathrm{d^2}x}{\dd{t}^2}=-m_gg \end{align}

　高校物理でも、これらは同じとして計算していました。
　一般相対性理論では、この$m_i=m_g$を等価原理としています。これが任意の物体において等しいことから、物体ごとに座標変換を変更せずともMinkowski時空をとれます。これにより重力を局所的に打ち消せるため、等価原理は、時空は局所的にはMinkowski時空であることを保証しています。すなわち、局所的には特殊相対性理論が成立することを意味するのです。

一般相対性原理

　これは、簡単に言ってしまうと、時空に絶対な座標は存在しないということを要請しています。どのような座標を我々がとっても変わらないような理論であるということです。生じている物理現象は同じなのですから、デカルト座標をとるか極座標をとるかで結果が変わってしまうような理論は整合性が取れているとは言えません。そのため、この原理は物理学を記述する上で極めて自然な要請であると言えます。

　以上の2つの原理から一般相対性理論は出発しています。では、次に重力はどのように記述できるか見ていきましょう。

1.2 時空の幾何学の基礎

　Minkowski時空では直交座標に対して光は直進するとされていますが、重力のある空間ではその限りではないことが知られています。その重要な例が重力レンズ効果です。非常に強い重力源が存在する場合、その付近を通過する光の軌道は曲げられる現象であり、実際に観測されています。そのため、重力は「時空の曲がり」によって記述できると考えられます。数学的にはRiemann幾何学を用いて定式化されています。
　時空の曲がりは計量を用いて記述できます。特殊相対性理論では計量として$\eta_{\mu\nu}=\mathrm{diag}(1,-1,-1,-1)$を採用していました。一般相対性理論では計量としてより一般的な2階対称テンソル$g_{\mu\nu}$を採用します。そのため、線素は次の形になります。
\begin{align} 　\dd{s}^2 = g_{\mu\nu}\dd{x^\mu}\dd{x^{\nu}} \end{align}
　
　また、曲がった空間では「平行移動」が必ずしも向きを保ちません。実際に例を考えてみるとしっくりくると思います。ここでは、地球儀の上で矢印を平行移動させることを考えてみましょう。
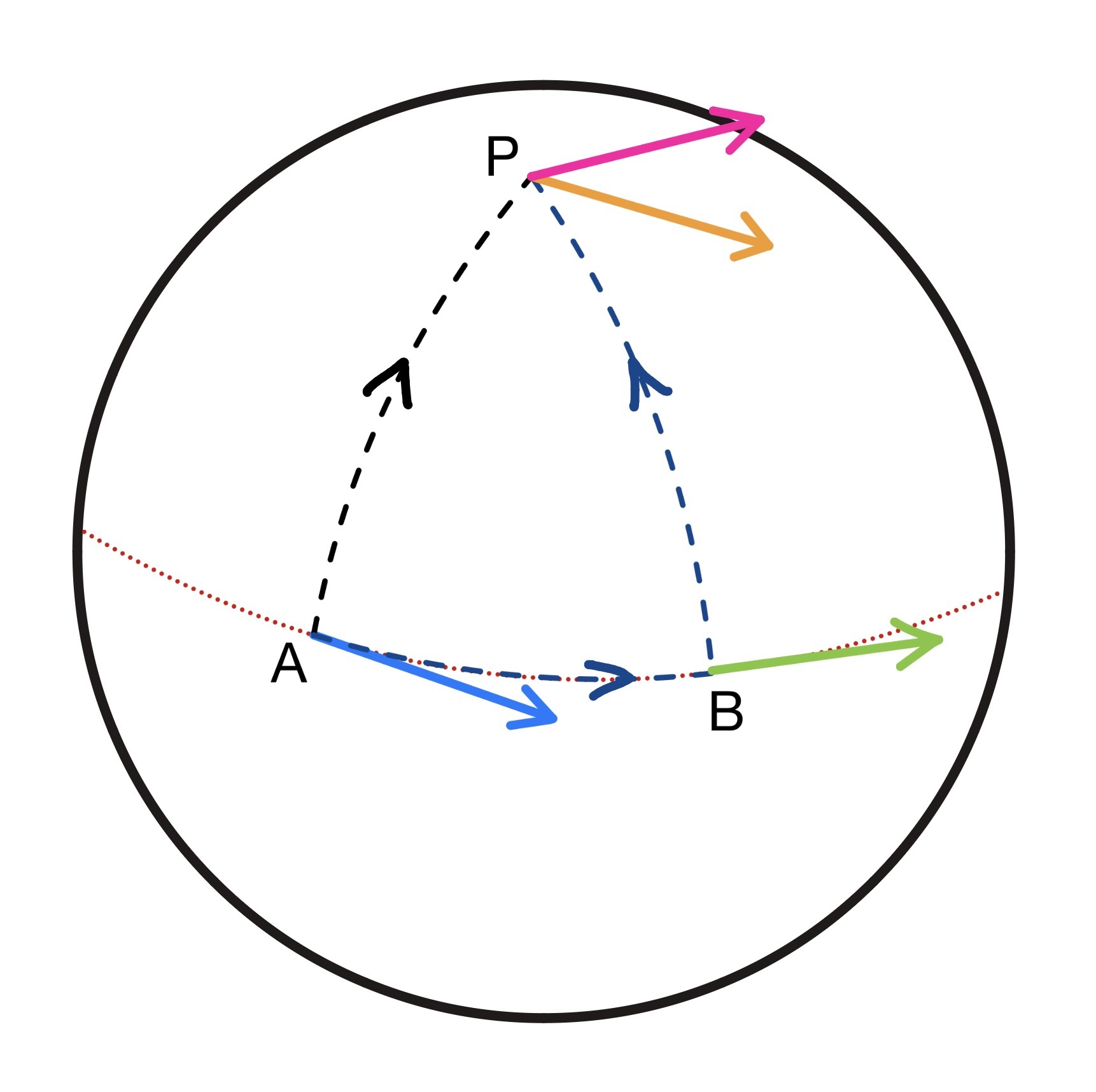曲がった空間での平行移動
　図のように、赤道上の点Aにある、赤道に沿った水色のベクトルを2種類の経路で北極Pに平行移動させることを考えます。まずは、経線にそってA$\to$Pへと平行移動させる経路です。この経路で移動した場合は、北極Pではオレンジ色のベクトルのようになります。もう一つの経路として、最初に赤道に沿ってA$\to$Bへと移動させたのちに、経線に沿ってB$\to$Pへと平行移動させる経路です。この場合は、点Bでは緑色のベクトルのようになり、これを移動させることを考えると、北極Pではピンク色のベクトルのようになります。すると、同じベクトルを平行移動させたにもかかわらず、北極Pでは向きが変わっていることがわかります。これが曲がった空間での特有の性質です。
　逆に、平行移動したときの変化を用いることで、空間がどれくらい曲がっているかを表現する曲率を扱うことができます。Riemann幾何学では、ベクトルやテンソルの「平行移動」を共変微分$\nabla_\mu$で表現します。共変微分を用いて、空間の曲がり具合を記述するRiemannテンソルを定義します。

　この定義の意味を考えておきます。$\nabla_\rho\nabla_\sigma$は先に$\nabla_\sigma$で「平行移動」させたのちに$\nabla_\rho$で「平行移動」させており、$\nabla_\sigma\nabla_\rho$は先に$\nabla_\rho$で「平行移動」させたのちに$\nabla_\sigma$で「平行移動」させています。そのため、どちらも同じ点へとベクトルを「平行移動」させています。そのため、$\qty[\nabla_\rho,\nabla_\sigma]$は、同じ点に2つの経路で平行移動させたときにどれくらいの違いが生じるかを評価する作用素となります。
　具体的に計算すると、これは次のように計算されます。
\begin{align} R^{\mu}_{\:\:\nu\rho\sigma}&=\partial_\rho\Gamma^\mu_{\:\:\nu\sigma}-\partial_\sigma\Gamma^\mu_{\:\:\nu\rho}+\Gamma^\mu_{\:\:\alpha\rho}\Gamma^\alpha_{\:\:\nu\sigma}-\Gamma^\mu_{\:\:\alpha\sigma}\Gamma^\alpha_{\:\:\nu\rho} \\ \Gamma^\rho_{\:\:\mu\nu}&=\frac{1}{2}g^{\rho\sigma}\qty(\partial_\mu g_{\nu\sigma}+\partial_\nu g_{\sigma\mu}-\partial_\sigma g_{\mu\nu}) \end{align}
　Riemannテンソルを用いて、一般相対論で用いる様々な物理量を定義しておきます。

　ここでは示しませんが、RicciテンソルとEinsteinテンソルは対称テンソルです。
　これらを用いて、重力場の基礎方程式を考えます。

1.3 Einstein方程式

　一般相対性理論の基礎方程式であるEinstein方程式は次のような式です。

　ただし、$G$はNewton力学での万有引力定数、$c$は光速です。
　解析力学になれている方向けに書くと、これは次のEinstein-Hilbert作用より導かれます。

\begin{align} S_{\text{EH}} &= \int\qty(\mathcal{L}_\text{M}+\mathcal{L}_\text{G})\sqrt{-g}\:\mathrm{d}^4x\: ＝ \:S_\text{M}+S_\text{G} \\ S_{\text{M}} &= \int\mathcal{L}_\text{M}\sqrt{-g}\:\mathrm{d}^4x \\ S_{\text{G}} &= \int\mathcal{L}_\text{G}\sqrt{-g}\:\mathrm{d}^4x \end{align}
　ただし、$g=\det g_{\mu\nu}$であり、$\mathcal{L}_\text{M}$は物質場のLagrangian、$\mathcal{L}_\text{G}$は重力場のLagrangianです。
　重力場の作用は次の形で書かれます。
\begin{align} 　S_\text{G}=\frac{1}{2\kappa}\int R\sqrt{-g}\:\mathrm{d}^4x \end{align}
　$R$は先ほど導入したRicciスカラーです。$\kappa$は係数であり、Einstein方程式と比較すると直ちにわかるように$\kappa=8\pi G/c^4$となります。
　この作用は、座標変換で不変なことからLagrangianがスカラーになっていることと、Newton重力がPoisson方程式が2回微分までを含むことから$g_{\mu\nu}$の3階以上の高階微分を含まないというアナロジーから定まっています。先ほどの章で、重力は空間の曲がりで記述され、これはRiemann幾何学ではRiemann曲率テンソルを用いて記述できることを見ました。Riemann曲率テンソルを用いて定められた量で、スカラーであり、かつ$g_{\mu\nu}$の高階微分を含まないものの代表的な例は、Ricciスカラー$R$です。そのため、これに不変体積要素$\mathrm{d}^4x\sqrt{-g}$を掛け合わせたものから作用を構成しています。
　物質場については、その変分から2階対称テンソル$T_{\mu\nu}$を定義します。
\begin{align} T_{\mu\nu}\coloneqq \frac{2c}{\sqrt{-g}}\qty[\partial_\alpha\qty{\frac{\partial\qty(\mathcal{L}_\text{M}\sqrt{-g})}{\partial\qty(\partial_\alpha g^{\mu\nu})}}-\frac{\partial\qty(\mathcal{L}_\text{M}\sqrt{-g})}{\partial g^{\mu\nu}}] \end{align}
　物質場の変分はこの$T_{\mu\nu}$により記述されます。以上を用いて、Einstein-Hilbert作用について計量の変分をとることでEinstein方程式が得られます。
　この式について少し噛み砕きます。左辺の$G_{\mu\nu}$は1.2で導入されたEinsteinテンソルであり、時空の曲がり具合を表しています。$T_{\mu\nu}$はエネルギー運動量テンソル(Stress-energy tensor)と呼ばれる2階対称テンソルで、時空中にどんな物質が存在しているかを表しています。また、係数については、時空の曲がりが小さい場合に、Newton力学と理論が整合するように調整されています。
　よって、この式は「時空中の状態を指定した時にその時空にはどのような重力が生じるか」を定める式になっています。両辺とも2階対称テンソルであるため、この式は計量$g_{\mu\nu}$についての10元連立2階非線形微分方程式になっています。

1.4 Schwarzschild解

　では、Einstein方程式を実際に解いてみましょう。と言いたいところですが、これを解くのはほぼ不可能に近いです。微分方程式を解いたことがあれば、10元連立の2階非線形なんて解けるわけないのが容易に想像されると思います。そこで、物理学者たちは式を簡単にする仮定を置いてEinstein方程式を解くことを考えました。
　その最も代表的な解であるSchwarzschild解について今回は述べます。これは1916年に、ドイツの物理学者Karl Schwarzschildによって導かれたEinstein方程式の解析解です。
　これは次の仮定を置いてEinstein方程式を解いています。

1. 真空解である。
2. 球対称時空である。

　それぞれの仮定について簡単に説明します。
　仮定1はシンプルで、時空に何も無い状態を考えることに対応します。数式的には、$T_{\mu\nu}=0$とすることに対応します。これでは何か意味がある結果が得られないような気がします。しかしながら、星が作る重力などを計算する際に、我々が興味があるのはその星の外側の空間の重力であるため、十分に意味のある結果を得ることができます。そのため、この仮定を置いて得た解は、星の外部のみを正しく記述していることに注意が必要です。(これについては3.1で再び述べます。)
　仮定2は、物理的解釈としては「特別な方向が存在しない」ことに対応します。どの方向を眺めても同じような時空になって欲しいというイメージです。より数式的には、2次元球面を示す計量がそのまま残ることに対応します。また、この要請を課すと、適切な座標変換により計量を対角化することが可能になり、$g_{00},g_{11}$を計算するのみで完了です。
　これらの仮定を置いたときの解がSchwarzschild解です。これは次の形になります。

　この解を得るためにはだいぶしんどい計算を頑張る必要がありますが、今回はこれを認めます。（この手計算に私は1日かかりました…。）この式を見ると、計量が時間に依存していない静的解(static)であることが分かります。そのため、次の定理が成立します。

　また、$r=0,2M$で計量が発散することが確認できます。このように、計量が発散するような点を特異点といいます。特異点には、座標変換により取り除くことができる特異点と、どのように座標変換しても取り除くことのできない真の特異点が存在します。真の特異点では、我々の知っている物理法則が全く適用できません。これを判別するための物理量がKrestchmannスカラーです。

　Krestchmannスカラーが発散する点が真の特異点であり、そうでない場合は座標変換で取り除くことができます。Schwarzschild解では、Krestchmannスカラーは次のようになります。

\begin{align} K\propto r^{-6} \end{align}

　これより、$r=0$が真の特異点であり、$r=2M$の特異性は座標変換により取り除くことができます。これについては2.3でより詳しく扱います。

1.5 ブラックホール

　では、特異性が取り除かれる$r=2M$には何か物理的に特別な意味はないのでしょうか。これを議論するために、Schwarzschild時空中で$r>2M$において動径方向($r$方向)に外向きに光を発射するという状況を考えてみます。以下の議論では、式の簡略化のために$r_g\coloneqq2M$という記号を導入しておきます。
　
$r_0\to r_1$への光の伝播
　
　半径$r_0(>r_g)$の位置にいる光源から、半径$r_1(>r_0)$にいる観測者に向けて光を発射します。光が発射されてから観測者がこれを受け取るまでの時間$\Delta t$を求めてみましょう。
　動径方向に伝わる光の経路は$\dd{s}^2=0$を満たすため、次式が成立します。

\begin{align} &\qty(1-\frac{r_g}{r})\dd{t}^2-\qty(1-\frac{r_g}{r})^{-1}\dd{r}^2=0 \\ \\ & \therefore \quad \frac{\dd{r}}{\dd{t}} = 1-\frac{r_g}{r} (> 0) \end{align}

　これを用いて$\Delta t$を計算してみます。
\begin{align} \Delta t & = \int_0^{\Delta t}\dd{t} \\ & = \int_{r_0}^{r_1} \frac{\dd{t}}{\dd{r}}\dd{r} \\ & = \int_{r_0}^{r_1} \frac{1}{1-r/r_g}\dd{r} \\ & = r_1-r_0+r_g\log\qty(\frac{r_1-r_g}{r_0-r_g}) \end{align}

　ここで、光源の位置を$r=r_g$に近づける極限をとってみます。
\begin{align} \Delta t = r_1-r_0+r_g\log\qty(\frac{r_1-r_g}{r_0-r_g}) \longrightarrow \infty\quad(r_0\to r_g) \end{align}

　このように、$r_0\to r_g$では$\Delta t$は発散してしまいます。
　この結果を物理的に解釈すると、「$r=r_g$から発した光は観測者に届かない」ということになります。つまり、$r< r_g$の領域から光は脱出することができないということです。すなわち、この領域こそがブラックホールなのです。$r=r_g$はブラックホールの表面の位置を表しており、一般相対性理論ではこれを事象の地平面(Event horizon)と呼びます。Schwarzschild解は、半径$r=2M$の回転していないブラックホールを含んだ解になっているということになります。 　

2. Penrose Diagram

　ここからがこの記事の本題である、Penrose diagramについてです。
　まずは、Penrose diagramを描くための「宇宙を上手く縮める」方法である共形変換について述べます。その後、最初は描き方のイメージを確かにするために、簡単な場合であるMinkowski時空のPenrose diagramを導入します。最後に、今回の主題であるSchwarzschild解のPenrose diagramに挑んでみます。　

2.1 共形変換

　我々が時空構造を把握しづらい理由の一つに、「時空が無限に広がっているから」というものがあります。時空の構造を視覚的にわかりやすくするためには、まずは目に見える範囲に時空を落とし込む必要があります。そこで、これから議論する共形変換という概念を用います。
　以下、4次元擬リーマン多様体(我々の考えている宇宙の数学的モデルです。)を考え、計量$g^{\mu\nu}$によって線素を次のように定めます。
\begin{align} \mathrm{d}s^2\coloneqq g_{\mu\nu}(x)\mathrm{d}x^{\mu}\mathrm{d}x^{\nu} \end{align}

　それでは、共形変換を定義しましょう。

　 数式的な定義を見てもあまりイメージが湧かないので、この変換の直感的な意義を与えます。

　この性質は何が嬉しいのでしょうか。ここで、特殊相対論でのMinkowski時空について考えてみます。Minkowski時空では、世界線が通過することを許す領域として光円錐を考えました。光はnullな軌道を描き、それはMinkowski時空では45°の直線を描くことから、この光円錐を考えていました。粒子は光速を超えて運動することを許されていないため、光円錐により世界線を制限するということは、｢情報は光速を超えて伝達されない｣という因果律(Causality)を定めるということになります。
　局所的に角度が変わらないということは、各点での光円錐の構造が保存されるということで、これは時空の因果構造を不変に保つということに他なりません。これが共形変換を考える一番大きなモチベーションです。
　さらに、ここでは$\Omega(x)$にもうひとつ条件を課したいと思います。Penrose diagramは無限に広い時空を有限の広さの図に落とし込む必要があります。そのため、$\Omega(x)$として次を満たすようなものを考えます。

\begin{align} \Omega(x)\to0\quad\qty(x\to\infty) \end{align}

　このような$\Omega(x)$を用いた共形変換を特に、共形コンパクト化といいます。

2.2 2次元Minkowski時空のPenrose diagram

　さて、では実際にPenrose diagramを書いてみましょう。最初なので、まずは最も簡単な例である2次元Minkowski時空のPenrose diagramを考えます。以下、順番に計算をしていきましょう。
　線素は次の形で与えられます。
\begin{align} \mathrm{d}s^2=\mathrm{d}t^2-\mathrm{d}x^2 \end{align}
　ここで、null座標$\qty(u,v)$を導入します。
\begin{equation} \left\{ \, \begin{aligned} & u = t-x \\ & v = t+x \end{aligned} \right. \end{equation}

　これを用いると線素は次の形になります。

\begin{align} \mathrm{d}s^2=\mathrm{d}u\mathrm{d}v \end{align}

　これより、計量は次のように書けます。

\begin{align} g_{\mu\nu}=\frac{1}{2} \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \end{align}

　ここで、次の座標変換を考えます。

\begin{equation} \left\{ \, \begin{aligned} \bar{u} &= 2\arctan u \\ \bar{v} &= 2\arctan v \end{aligned} \right. \end{equation}

　このとき、$\bar{u},\bar{v}$のとる範囲は$-\pi\leq\bar{u},\bar{v}\leq\pi$であり、線素は次のように書けます。

\begin{align} \mathrm{d}s^2=\qty(2\cos\frac{\bar{u}}{2}\cos\frac{\bar{v}}{2})^{-2}\mathrm{d}\bar{u}\mathrm{d}\bar{v} \end{align}

　そのため、計量は次の形になります。

\begin{align} g_{\mu\nu}=\frac{1}{2}\qty(2\cos\frac{\bar{u}}{2}\cos\frac{\bar{v}}{2})^{-2} \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \end{align}

　よって、

\begin{align} \Omega^2(x)=\qty(2\cos\frac{\bar{u}}{2}\cos\frac{\bar{v}}{2})^2 \end{align}

としたときの共形変換を考えることによって、Minkowski時空を有限領域へと変換することができます。
　これは共形変換であるため、光円錐が不変のはずです。これを実際に確認してみましょう。
　座標変換後の線素を$\mathrm{d}\bar{s}^2$としたとき、次の関係式が成立します。
\begin{align} \mathrm{d}\bar{s}^2=\Omega^2(x)\mathrm{d}s^2 \end{align}
　座標変換前のnullな軌道とは、$\mathrm{d}s^2=0$となるものと定まっていました。この関係式より、座標変換後のnullな軌道もまた$\mathrm{d}\bar{s}^2=0\;\;(\because \Omega(x)\neq 0)$を満たすため、その方向は45°で不変に保たれます。以上の議論から、たしかに因果律が保たれていることが確認できました。
　では、$\bar{u}\bar{v}$平面上でMinkowski時空を描いてみましょう。$\bar{u},\bar{v}$が取りうる値の範囲に注意すると、次の図のようになります。

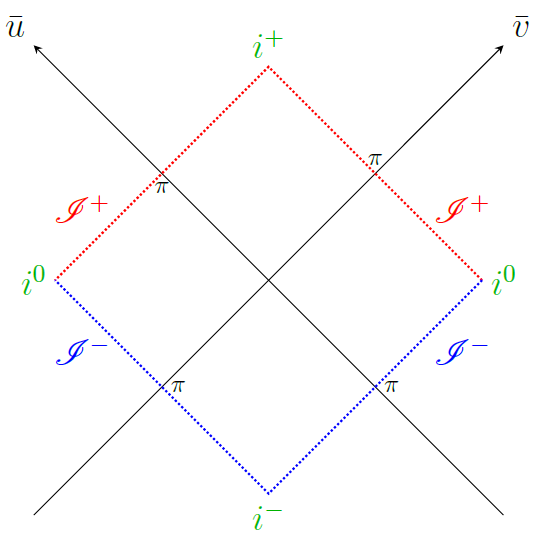Minkowski時空のPenrose diagram

これがMinkowski時空のPenrose diagramです。この正方形の領域が、Minkowski時空と対応しています。
ここで、図1にも表れているようなPenrose diagramに特有の各領域や点の名称を定義しておきましょう。

• $i^+ \:\colon\bar{u}=\bar{v}=\pi\quad$ future infinity（無限遠の未来）
• $i^- \:\colon\bar{u}=\bar{v}=-\pi\quad$ past infinity（無限遠の過去）
• $i^0 \:\:\colon\bar{u}=\pm\pi,\bar{v}=\mp\pi\quad$ spatial infinity（空間的無限遠）
• $\mathscr{I}^+\colon\bar{v}=\pi,\abs{\bar{u}}\neq\pi \:\mathrm{or}\: \bar{u}=\pi,\abs{\bar{v}}\neq\pi\quad$ future null infinity（null線に沿った無限の未来）
• $\mathscr{I}^-\colon\bar{v}=-\pi,\abs{\bar{u}}\neq\pi \:\mathrm{or}\: \bar{u}=-\pi,\abs{\bar{v}}\neq\pi\quad$ past null infinity（null線に沿った無限の過去）

それぞれの意味を簡単に述べておきましょう。時空の中を運動する粒子が描く世界線は$i^-$と$i^+$を結ぶような曲線になり、光速で運動すると、いずれ$\mathscr{I}^+$上に行きつきます。このような特徴的な点や領域にラベルを振っています。

　ここまでは2次元のMinkowski時空を用いて議論してきましたが、これを4次元に拡張することは比較的簡単です。4次元のMinkowski時空の線素は、極座標表示を取ると次のようになります。

\begin{align} \mathrm{d}s^2=\mathrm{d}t^2-\mathrm{d}r^2-r^2\mathrm{d}\Omega^2\quad(\mathrm{d}\Omega^2=\mathrm{d}\theta^2+\sin^2\theta\mathrm{d}\phi^2) \end{align}

　よって、2次元の場合の議論に加えて、各点に2次元球面が埋め込まれたような構造になっています(また、$r$についても非負実数しかとらないため領域に制限が加わりますが、Penrose diagramの形自体に変化はありません)。そのため、本質的な議論は2次元の場合で尽きていると言ってしまっていいでしょう。

2.3 Schwarzschild時空のPenrose diagram

　
　それでは、1.4で紹介したSchwarzschild解のPenrose diagramを描いてみましょう。
　Schwarzschild解は次のような形をしていました。
\begin{align} \mathrm{d}s^2=\qty(1-\frac{2M}{r})\mathrm{d}t^2-\qty(1-\frac{2M}{r})^{-1}\mathrm{d}x^2-r^2\mathrm{d}\Omega^2 \end{align}

　これをテクニカルに変形していきます。
　1.4にて、Schwarzschild計量は$r=0,2M$で発散するが、物理が破綻する真の特異点は$r=0$のみであり、$r=2M$での特異性は取り除くことが出来るとしました。以下では、$r=2M$での特異性を取り除くために、かなりテクニカルな座標変換を行います。 また、計算の簡単のために2次元Schwarzschild座標にて考えます。
まずは次のtortoise座標$r^\ast$を導入します。

\begin{align}   r^\ast&\coloneqq r+2M\ln\abs{\frac{r}{2M}-1} \\   &\to \:\dd{r^\ast}=\qty(1-\frac{2M}{r})^{-1}\dd{r} \end{align}

　このとき、計量は次の形になります。

\begin{align}   \dd{s^2}=\qty(1-\frac{2M}{r})\dd{t^2}-\qty(1-\frac{2M}{r})\dd{r^\ast}^2 \end{align}

　次にnull座標$(u,v)$を導入します。
\begin{equation}   \left\{ \,     \begin{aligned}     & u=t-r^\ast \\     & v=t+r^\ast     \end{aligned} \right. \end{equation}

　これを用いると、計量は次の形になります。

\begin{align}   \dd{s^2}=\qty(1-\frac{2M}{r})\dd{u}\dd{v} \end{align}

　最後に、Kruskal座標$(\bar{u},\bar{v})$を導入します。

\begin{equation}   \left\{ \,     \begin{aligned}     & \bar{u}=\mp \exp\qty(-\frac{u}{4M}) \quad(+\:\colon\:r<2M,\; -\:\colon\:r>2M)\\     & \bar{v}= \exp\qty(-\frac{v}{4M})     \end{aligned} \right. \end{equation}
　Kruskal座標の定義されている範囲は、$0<\bar{v}$となります。
　この座標の下では、計量は次の形になります。

\begin{align}   \dd{s^2}=\frac{32M^3}{r}e^{-r/2M}\dd{\bar{u}}\dd{\bar{v}} \end{align}

この計量を見ると、確かに$r=2M$での発散は取り除かれ、$r=0$の特異性のみが残されています。
　さて、この計量どこかで見覚えがありませんか？そう、この形はMinkowski時空でnull座標を導入した時とかなり似た形をしています。そこで、2.2と同じような座標変換を考え、新たな座標$(\tilde{U},\tilde{V})$を導入します。

\begin{equation} \left\{ \,     \begin{aligned}     & \tilde{U} = 2\arctan \bar{u} \\     & \tilde{V} = 2\arctan \bar{v}       \end{aligned} \right. \end{equation}

　この変換は2.2で確認した通り共形変換であり、計量は次の形になります。
\begin{align}   \dd{s}^2=\frac{32M^3}{r}e^{-r/2M}\frac{\dd{\tilde{U}\dd{\tilde{V}}}}{\cos^2\tilde{U}\cos^2\tilde{V}} \end{align}

　Penrose diagramを描く前に、この計量の性質について少し考察してみましょう。
　まずは光円錐についてです。Minkowski時空の場合と同じく、どの点においてもnullな軌道は45°に保たれているので、光円錐の形は不変です。
　次に、真の特異点である$r=0$と、事象の地平面である$r=2M$に対応する領域を考えます。Kruskal座標に戻って$\bar{u}\bar{v}$を$r<2M$で計算してみます。
　
\begin{align}   \bar{u}\bar{v}=e^{r/2M}\qty(1-\frac{r}{2M}) \end{align}
　これより、次のような対応がわかります。

　\begin{align} 　\left\{ \,     \begin{aligned}     r=0 &\Longleftrightarrow \bar{u}\bar{v}=1 \\ &\Longleftrightarrow \tan\frac{\tilde{U}}{2}\tan\frac{\tilde{V}}{2}=1 \\ &\Longleftrightarrow \tilde{U}+\tilde{V}=\pm\pi \\     r=2M &\Longleftrightarrow \bar{u}\bar{v}=0 \\ & \Longleftrightarrow \tan\frac{\tilde{U}}{2}\tan\frac{\tilde{V}}{2}=0 \\ & \Longleftrightarrow \tilde{U}=0 \;\mathrm{or}\; \tilde{V}=0     \end{aligned} \right. \end{align}
　最後に、Kruskal座標は$0<\bar{v}$でのみ定義されていたため、共形変換後の座標の定義域も$0<\tilde{V}$となります。しかし、計量を眺めたとき、$\tilde{V}\leq0$でも特異な振る舞いをするわけではありません。そのため、$\tilde{V}\leq0$へと自然と拡張することができます。以下では、定義域を拡張して議論していきます。
　以上でPenrose diagramを書く準備は整いました。Schwarzschild時空のPenrose diagramは次の図のようになります。

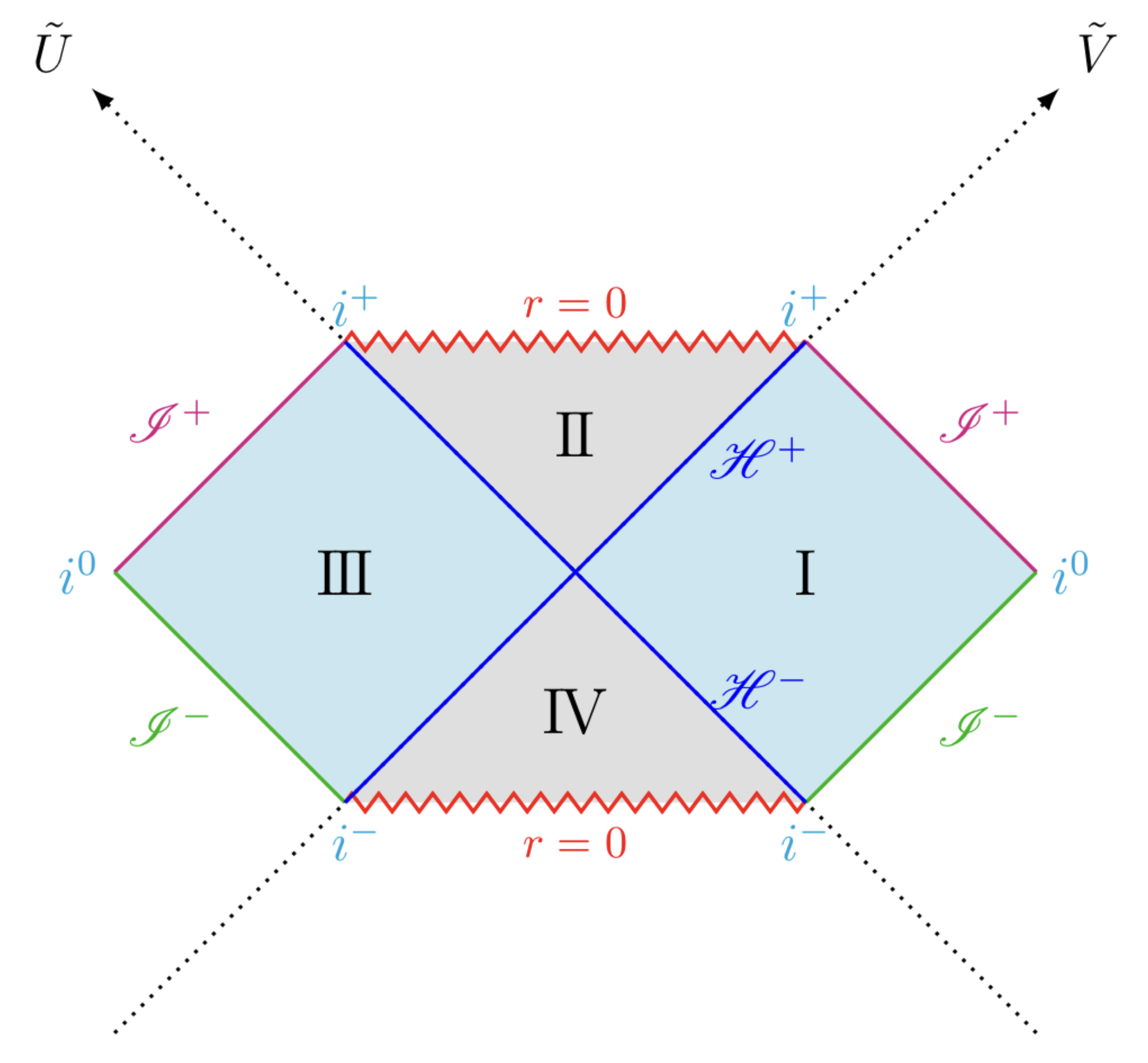Schwarzschild時空のPenrose diagram
　このようにして、冒頭に紹介したSchwarzschild解のPenrose diagramを描くことができました。Minkowski時空の場合と比べると、新たに$\mathscr{H}^\pm$と記号が増えており、これが未来、過去における事象の地平面$r=2M$を表しています。($\mathscr{H}$を採用しているのはHorizon由来です。)
　では、この図についてもっと深く解析するために、光円錐を考えてみましょう。
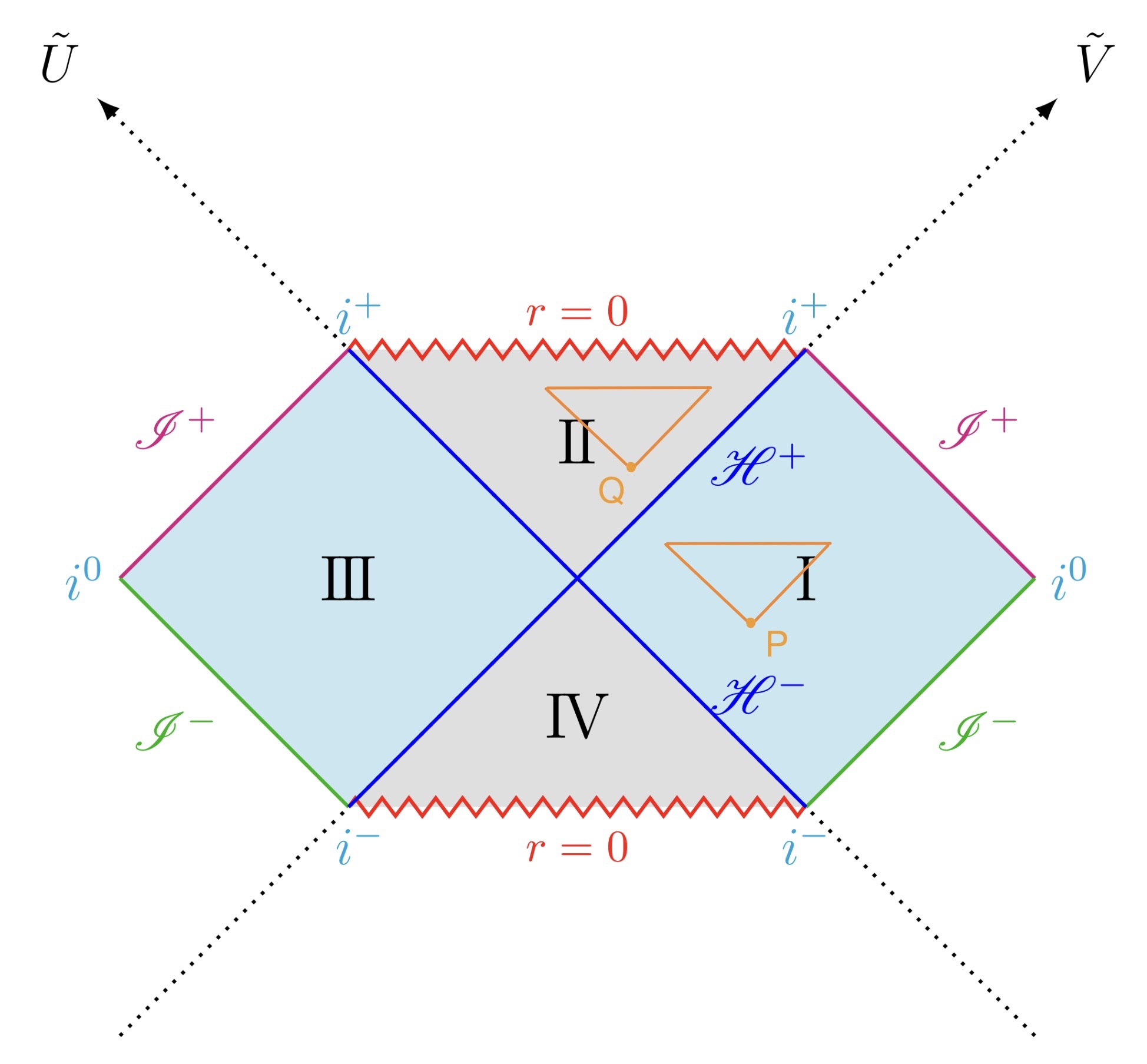Penrose diagramと光円錐

　領域Ⅰ内の点Pと領域Ⅱ内の点Qのそれぞれにおいて、未来方向の光円錐を描いています。
　まずは領域Ⅰについて考えてみましょう。領域Ⅰとは、我々がいる時空領域のことであり、点Pを通過した粒子の軌道を考えると、$\mathscr{I}^+$や$i^+$に到達するものに加えて、$\mathscr{H}^+$を通り抜けて領域Ⅱへと入っていくものも考えられます。
　では、領域Ⅱではどうでしょうか。先ほどの点Pとは大きく変わり、点Qを通過したどんな粒子の軌道も、たとえそれが光であっても、いずれは特異点である$r=0$に到達し、領域Ⅰへは戻ることなどはありません。
　さて、以上の考察から次のようなことが言えます。

　この結果は、$\mathscr{H}$が事象の地平面であり、領域Ⅱがブラックホールに対応していることと確かに一致します。1.5のような少々複雑な計算をしなくても、光円錐を考えるだけでその宇宙の時空構造がより直感的にわかるのは、Penrose diagramの強力な特徴です。
　ここから先は余談なのですが、領域Ⅲは領域Ⅰと対象な構造を持つ並行宇宙であり、領域Ⅳはホワイトホールであると解釈できます。また、領域Ⅲは形式的には領域Ⅰに対して時間が反転した宇宙であるため、ブラックホールとホワイトホールの対応が反転したりします。

3. ブラックホールの物理

　以上のように、Penrose diagramを描くことで、ブラックホールを含むSchwarzschild時空の構造を明らかにすることが出来ました。
　最後に、Penrose diagramの発展的内容や、ブラックホールの物理学について少し述べたいと思います。

3.1 重力崩壊する星のPenrose diagram

　再び、Schwarzschild時空とはなんであったかを見つめてみましょう。これはEinstein方程式の次の仮定を置いた厳密な解析解でした。

• 球対称時空である。
• 真空解である。

そして、Birkhoffの定理より、この解は静的解です。
よって、Schwarzschild時空の事象の地平面は無限の過去からずっと存在しているものということになります。
　しかしながら、我々はブラックホールが出来る具体的な過程をひとつ知っています。それは、非常に重い星が自身の重力によって潰れていく重力崩壊を起こしてブラックホールになるというものです。では、このようにしてブラックホールができる過程のPenrose diagramは書けるのでしょうか。
　答えはYesで次の図のようになります。

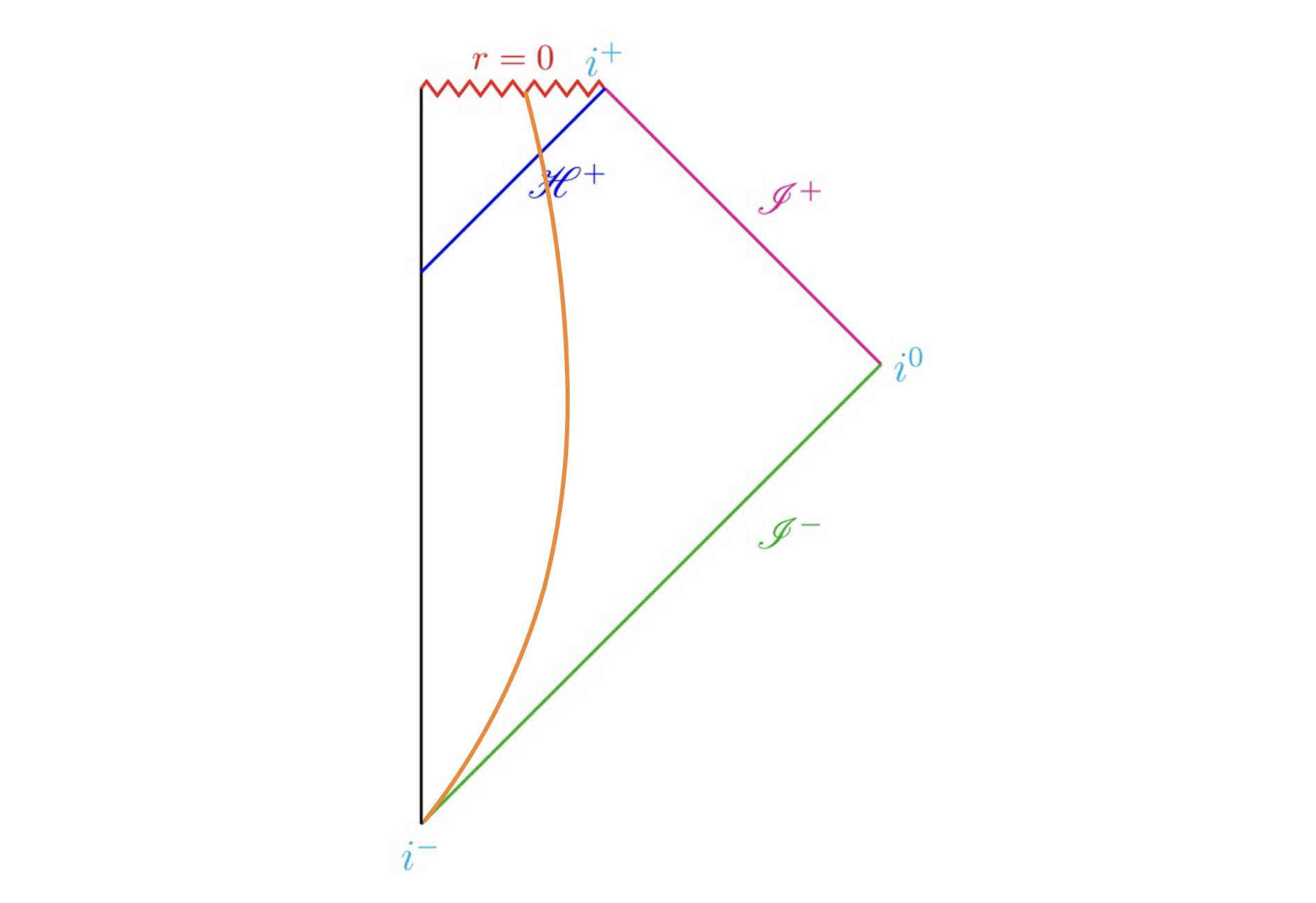重力崩壊する星のPenrose diagram

　オレンジの曲線は重力崩壊する星の表面に対応します。そのため、黒線とオレンジの曲線に挟まれた領域は真空ではないことから正しい図となっていません。しかしながら星の外部に関しては正しいPenrose diagramとなっています。星の内部については、これを完全流体と仮定したエネルギー運動量テンソルからSchwarzschild内部解が得られています。
　この図を見るとおり、過去では星であったものが、重力崩壊によりつぶれ、事象の地平面が生じる過程が描かれています。

3.2 特異点定理と宇宙検閲官仮説

　Penrose diagramを書く過程では深く触れていなかった特異点について、少し述べようと思います。
　Einstein方程式の解において、座標変換で取り除くことの出来ないような、計量を発散させる点のことを真の特異点としていました。以下では簡単のために真の特異点を単に特異点と呼びます。特異点では物理法則が破綻しており、一般相対性理論は、そのような理論自身を破綻させるような要素を内包しているという点でも非常に興味深い理論となっています。
　ここで、特異点について非常に重要な定理を紹介します。それは、HawkingとPenroseにより示された特異点定理です。

　それぞれ用語について補足します。
　光的捕捉面とは、簡単に言うと「光を外向きに放った時にその波面が膨張せずに留まってしまう」面のことです。直感的には、光が進もうとする運動が重力による影響によってつり合い、止まってしまうような面になります。よって、光的捕捉面が存在するということは強い重力場が存在することに対応します。
　エネルギー密度は$\rho\coloneqq T_{\mu\nu}u^\mu u^\nu$で定義されます。ただし、$T_{\mu\nu}$はエネルギー運動量テンソルであり、$u^\mu$はtimelikeなベクトル場です。(timelikeとは、ここでは$u^\mu u_\mu>0$であり、粒子の速度ベクトルなどはこれを満たします。）解釈としては、$T_{\mu\nu}u^\mu u^\nu$とは、4元速度$u^\mu$で動く観測者から見た時空のエネルギー密度に対応します。そして、エネルギー密度が正であることは、重力が引力であることに対応します。よってこの条件は、重力が斥力になるような変な時空は考えないということになります。
　最後に、測地線(Geodesic)についてです。測地線は、計量$g_{\mu\nu}$をもつ時空中を運動する粒子の軌道を決定する、いわば一般相対論における運動方程式であり、次の式で表されます。
\begin{align} \frac{\mathrm{d}^2x^\mu}{\dd{\tau}^2}+\Gamma^\mu_{\:\:\rho\sigma}\frac{\dd{x^\rho}}{\dd{\tau}}\frac{\dd{x^\sigma}}{\dd{\tau}}=0 \end{align}
　重力のみを受けて運動する質量をもつ粒子の運動は必ず測地線に沿うようになり、このような測地線をtimelikeな測地線と呼びます。timelikeな測地線上にはAffineパラメータと呼ばれるパラメータが定まり、これが固有時間$\tau$に一致します。次の図に示すように、粒子が$\tau=0$ではここにいて、$\tau=1$ではここにいるといった感じに測地線上に「名前」を振ることができます。
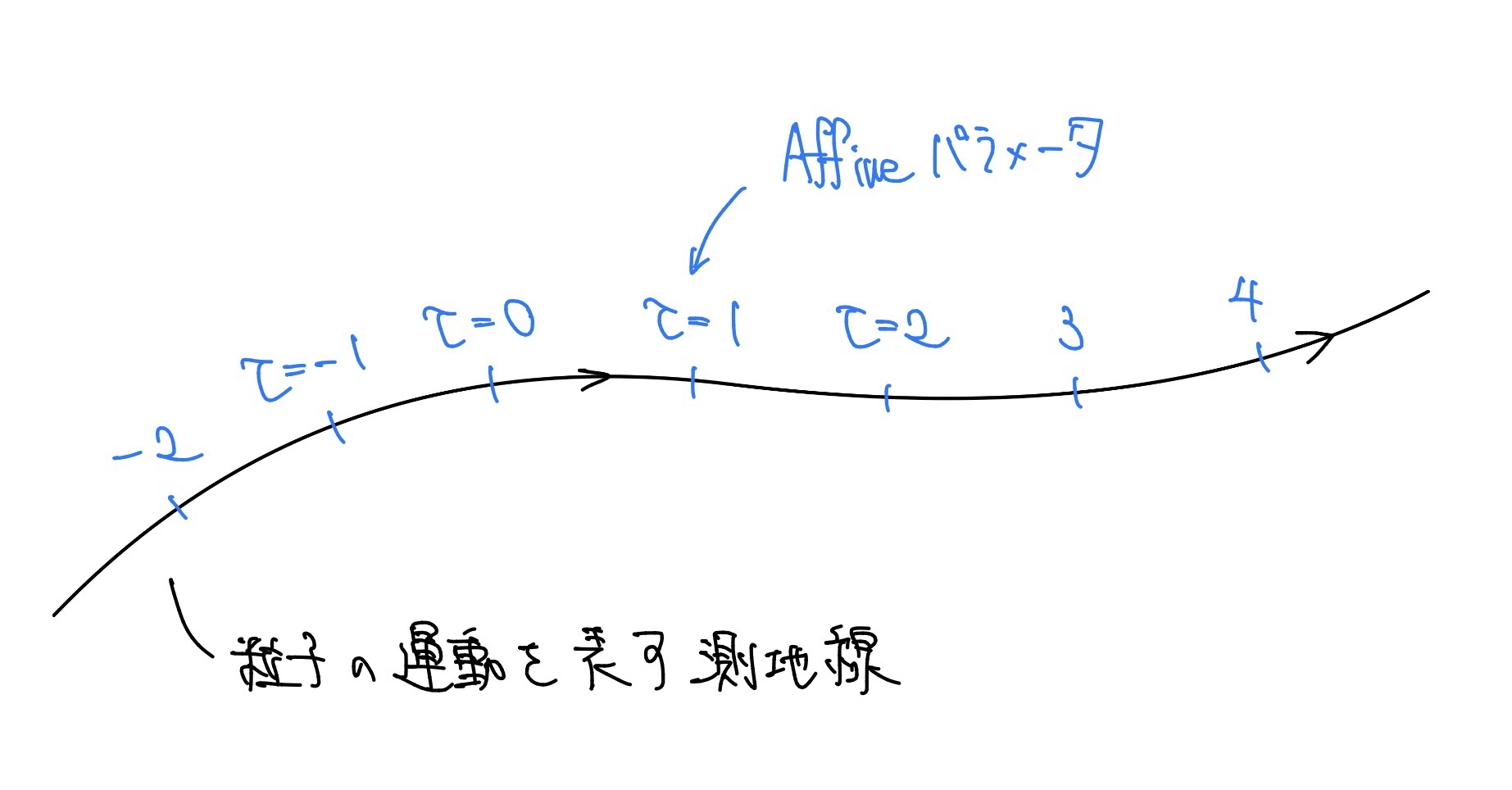測地線とAffineパラメータ
　光の軌道を表す測地線であるnullな測地線に対しても、同様にAffineパラメータを定めることができます。timelikeな測地線とnullな測地線をまとめて因果的測地線と呼び、ここからの議論では因果的測地線のAffineパラメータが重要な役割を果たします。
　では、「有限で延長不可能な測地線が存在する」ということの意味を考えます。そもそも、我々は特異点について議論したいはずで、どうして測地線についてここで考えているのでしょうか。これには、特異点の数学的な難しさが関係しています。これについては少し難しい話になるため、結論のみを認めてもよいです。一般相対論では、時空を滑らかな多様体とし、曲率を定義するために計量が2階微分可能であることを要請しています。このため、計量が発散するような特異点は、もはや多様体上の点としては扱えないため、時空上の点を用いて特異点の存在を議論するためには工夫をする必要があります。そこで、これを測地線を用いて考えることにします。時空が特異である、すなわち特異点が存在することを次で定義します。

　これが特異点の存在に対応することを、Schwarzschild時空で確認してみましょう。粒子の軌道をPenrose diagram上で考えてみると、$i^-$と$i^+$を結ぶような軌道もあれば、次の図のように特異点$r=0$にぶつかる軌道も考えられます。

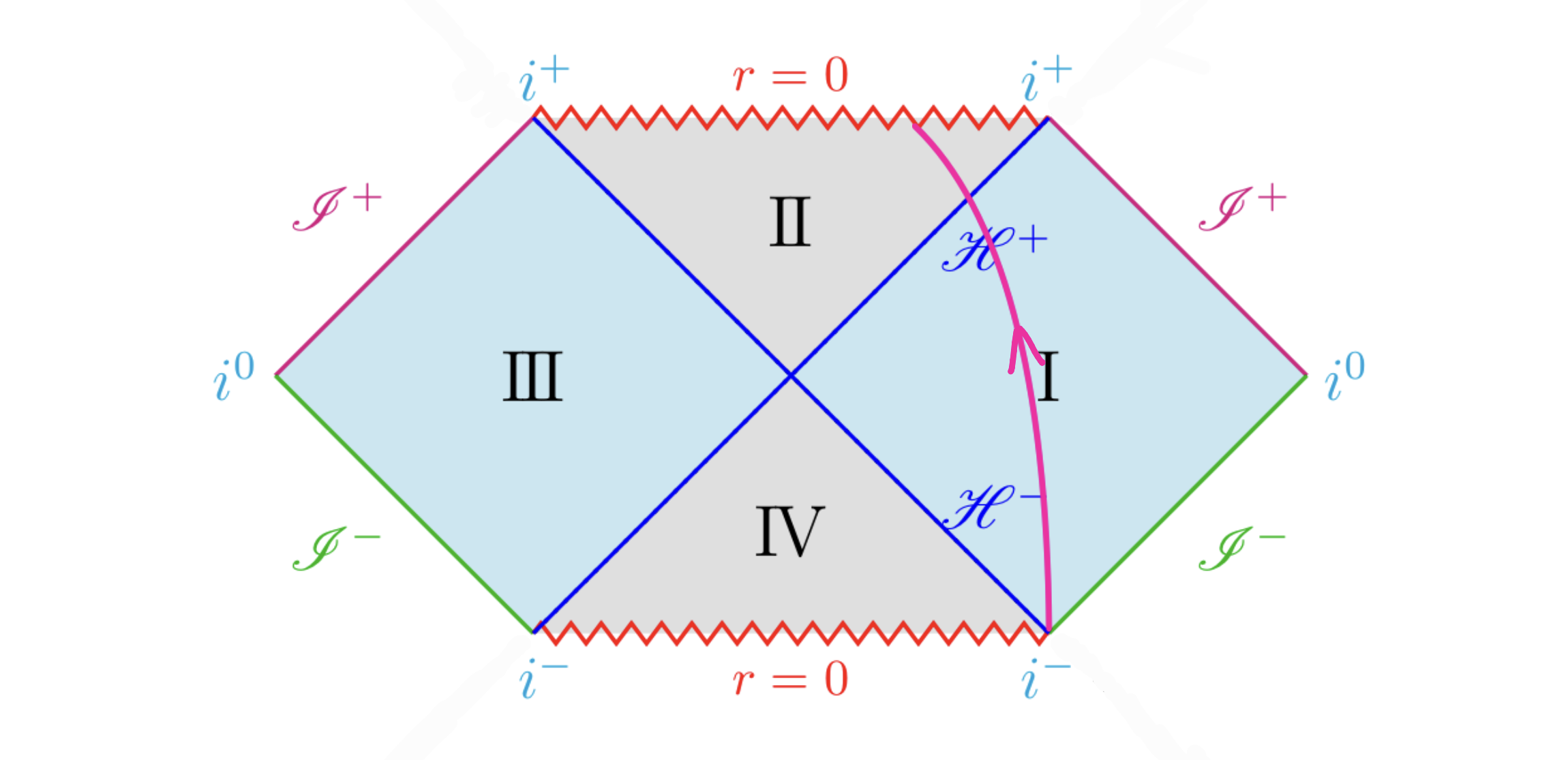未来に延長不可能な測地線

　特異点にぶつかってしまうため、このような測地線はAffineパラメータを未来へ無限に延長することができません。よって、特異点が存在する場合、これにぶつかるような測地線を考えればこれは有限で延長不可能であるため、良い定義になっていることがわかります。
　ここまでの長々とした準備を踏まえると、特異点定理は次のように解釈できます。

　これは物理的にとても不都合な主張のように見えます。一般相対性理論を考える限りでは、我々の宇宙には物理法則を破綻させるような点が必ず存在するというのです。すなわち、一般相対性理論がその理論自体を破綻させてしまうような点を生み出してしまうことになります。直感的にも、計量が発散して時空の構造がとんでもないことになっていそうな点が存在してしまっては困ることはなんとなくつかめるかと思います。
　しかしながら、実はこの宇宙において特異点が存在しても困らない領域が存在します。ここまで読んでくださった皆さんならもうおわかりでしょう。そう、ブラックホールの内部です。ブラックホールの内部であれば、物理法則がいくら破綻しようと、その現象は事象の地平面によって遮られ、我々の観測できる領域へは伝わりません。
　とはいえ、特異点がすべてブラックホールの内部になければならない理由は依然はっきりしていません。そのため、ブラックホールの外側に存在する特異点のことを裸の特異点と呼び、Penroseは次のような仮説を立てました。

　これは、まるで宇宙には｢検閲官｣のような存在がいて、特異点が生じる度にそれをブラックホールで覆い隠しているようだ、という意味から来ています。まだこれは仮説の段階であり、その証明・検証が待たれています。
特異点を隠そうとする検閲官

　ここで紹介したもの以外にも、ブラックホールに対しては様々な研究が行われています。ブラックホールが熱輻射をしていたり、ブラックホールが「蒸発する」という現象が理論的には考えられたりと、非常に面白い性質を持ちます。
　皆さんも、この記事を読んでブラックホールに少しでも興味を持っていただけたらうれしいです。ぜひ、星空を見上げたときには、我々の肉眼には映ることのない漆黒の天体に思いを馳せてみてください。