ランベルトのW関数の積分を解いたり, テトレーションをW関数で表したりした

ランベルトの$W$関数

定義

ランベルトの$W$関数は関数$f(x)=xe^x$の逆関数のことです. 次のように定義します.

ランベルトのW関数

関数$f:\mathbb{R}\to(-1/e,\,\infty),\,x\mapsto xe^x$の逆関数を
$$ f^{-1}(x)=W_0(x)\quad(-1\leq x) $$
$$ f^{-1}(x)=W_{-1}(x)\quad(x\leq-1) $$
と定める. このとき, $W_0$を主枝, $W_{-1}$を分枝と言う.

関数のグラフは以下のようになります.

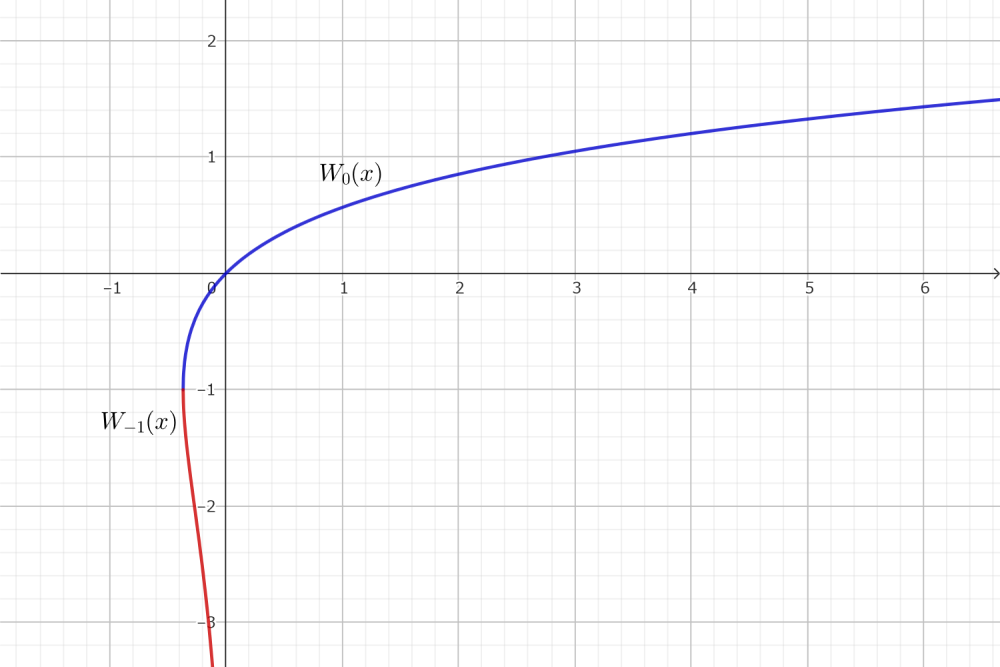ランベルトのW関数

$W_0$の級数展開

$-\dfrac{1}{e}\leq x\leq\dfrac{1}{e}$のとき, 次の式が成り立つ.
$$ W_0(x)=\sum_{n=1}^\infty\frac{(-n)^{n-1}}{n!}x^n $$

英語版WikipediaのLagrange inversion theorem(ラグランジュの反転公式)を参考に級数展開を求めていきます.

ラグランジュの反転公式 ($0$中心の展開)

$f(x)$が点$0$で解析的で$f(0)=0,f'(0)\neq0$を満たすとき
$\displaystyle f^{-1}(x)=\sum_{n=1}^\infty\lim_{t\to0}\left(\frac{d^{n-1}}{dt^{n-1}}\left(\frac{t}{f(t)}\right)^n\right)\frac{x^n}{n!}$

$f(x)=xe^x\,(-1\leq x)$とすると, $f^{-1}(x)=W_0(x)$である.
$$ W_0(x) =\sum_{n=1}^\infty\lim_{t\to0}\left(\frac{d^{n-1}}{dt^{n-1}}e^{-nt}\right)\frac{x^n}{n!} =\sum_{n=1}^\infty\frac{(-n)^{n-1}}{n!}x^n $$
を得る. ダランベールの収束判定法を用いると
$\left|\dfrac{\frac{(-n-1)^n}{(n+1)!}x^{n+1}}{\frac{(-n)^{n-1}}{n!}x^n}\right|=\left|-\dfrac{(n+1)^{n-1}}{n^{n-1}}x\right|=\left|\left(1+\dfrac{1}{n}\right)^{n-1} x\right|< e|x|<1$
よって, 収束半径は$1/e$です.
また, Wolfram Mathematicaで$x=\pm1/e$のときを調べると級数は収束したので, $-1/e\leq x\leq1/e$で級数は収束します.

ランベルトの$W$関数の積分

$$ \int_{-\infty}^{-1} -W_0(W_{-1}^{-1}(x))\,dx+\int_{-1}^0 -W_{-1}(W_0^{-1}(x))\,dx=\frac{\pi^2}{3} $$

$W_{-1}$の積分を$W_0$の積分で表す

$W_0(W_{-1}^{-1}(x))\,(x\leq -1)$と$W_{-1}(W_0^{-1}(x))\,(-1\leq x)$は$y=x$で線対称であることを示す.
$x\leq-1$のとき$-1\leq W_0(W_{-1}^{-1}(x))$より, $W_0(W_{-1}^{-1}(x))$を$W_{-1}(W_0^{-1}(x))$に代入して
$$ W_{-1}(W_0^{-1}(W_0(W_{-1}^{-1}(x))))=W_{-1}(W_{-1}^{-1}(x))=x $$
$W_0(W_{-1}^{-1}(x))\,(x\leq -1)$は$W_{-1}(W_0^{-1}(x))\,(-1\leq x)$の逆関数となっているから, $y=x$で線対称である.
よって, 次の等式を得られる.
$$ \int_{-1}^0 -W_{-1}(W_0^{-1}(x))\,dx=\int_{-\infty}^{-1} -W_0(W_{-1}^{-1}(x))\,dx-1 $$
これを求める積分に代入して
$$ \int_{-\infty}^{-1} -W_0(W_{-1}^{-1}(x))\,dx+\int_{-1}^0 -W_{-1}(W_0^{-1}(x))\,dx =2\int_{-\infty}^{-1} -W_0(W_{-1}^{-1}(x))\,dx-1 =2\int_{-\infty}^0 -W_0(W_{-1}^{-1}(x))\,dx =2\int_{-\infty}^0 -W_0(xe^x)\,dx $$
となる.

級数展開で積分を級数にする

$W_0(x)$の$x=0$中心のテイラー展開は
$$ W_0(x)=\sum_{n=1}^\infty \frac{(-n)^{n-1}}{n!}x^n\quad\left(|x|\leq\dfrac{1}{e}\right) $$
であり, $x\leq-1$のとき, $-\dfrac{1}{e}\leq xe^x<0$なので
$$ 2\int_{-\infty}^0 -W_0(xe^x)\,dx =-2\int_{-\infty}^0 \sum_{n=1}^\infty \frac{(-n)^{n-1}}{n!}(xe^x)^n\,dx $$

積分と無限和の入れ替えのために, 有界であることを示したい.

優関数$f$を
$$ f(x)=\begin{cases} x^2 e^x & (x\leq-2) \\ x+2+\frac{4}{e^2} & (-2< x\leq0) \end{cases} $$
と定めると, 任意の$x\leq0,\,N\in\mathbb{N}$に対して
$\displaystyle 0<\left|\sum_{n=1}^N \frac{(-n)^{n-1}}{n!}(xe^x)^n\right|< f(x)$となる.
$$ \int_{-\infty}^0 f(x) dx =\int_{-\infty}^{-2} x^2 e^x\,dx+\int_{-2}^0 \left(x+2+\frac{4}{e^2}\right)\,dx =2+\frac{18}{e^2}<\infty $$

これより, ルベーグの収束定理が使えて, 総和と積分を入れ換えると
$$ -2\int_{-\infty}^0 \sum_{n=1}^\infty \frac{(-n)^{n-1}}{n!}(xe^x)^n\,dx=-2 \sum_{n=1}^\infty \int_{-\infty}^0 \frac{(-n)^{n-1}}{n!}(xe^x)^n\,dx =-2 \sum_{n=1}^\infty \frac{(-n)^{n-1}}{n!}\int_{-\infty}^0 (xe^x)^n\,dx $$
となる.

残りの積分部分を計算する.

$$ \int_{-\infty}^0 (xe^x)^n\,dx $$
$y=-nx$とおくと, $dx=-\dfrac{dy}{n}$より
$$ =\dfrac{1}{n}\int_0^\infty \left(-\frac{y}{n}\right)^ne^{-y}\,dy =\dfrac{(-1)^n}{n^{1+n}}\int_0^\infty y^{(n+1)-1}e^{-y}\,dy =\dfrac{(-1)^n}{n^{1+n}}\Gamma(n+1) =\dfrac{(-1)^nn!}{n^{1+n}} $$
を得る.

よって, 求めた積分値から無限和を整理すると
$$ -2 \sum_{n=1}^\infty \frac{(-n)^{n-1}}{n!}\int_{-\infty}^0 (xe^x)^n\,dx =-2 \sum_{n=1}^\infty \frac{(-n)^{n-1}}{n!}\cdot\dfrac{(-1)^nn!}{n^{1+n}} $$
$$ =2 \sum_{n=1}^\infty \frac{1}{n^2} =\frac{\pi^2}{3} $$
となる.

また, この積分より
$$ \int_{-\infty}^0 W_0(xe^x)\,dx=-\frac{\pi^2}{6},\,\int_{-1}^0 W_{-1}(xe^x)\,dx=-\frac{\pi^2}{6}-\frac{1}{2} $$
を得る.

$x$の無限テトレーション$x^{x^{x^\cdots}}$を$W$関数で考える

$y=x^y,\,y=x^{x^y}$の概形の比較

$y=x^y$の概形

$y=x^y$はランベルトの$W$関数を用いて, $y$について解ける.
$$ y=x^y\Leftrightarrow \log y=y\log x\Leftrightarrow \left(\dfrac{1}{y}\right)\log\left(\dfrac{1}{y}\right)=-\log x $$
ランベルトの$W$関数を取ると
$$ \log\left(\dfrac{1}{y}\right)=-\log y=W(-\log x)\Leftrightarrow y=e^{-W(-\log x)} $$

$W$関数は2価の関数なので, それぞれの場合でグラフを考えると, 次のようになります.

!FORMULA[72][1114525241][0] $y=x^y$

$y=x^y$を構成する関数

$y=e^{-W_0(-\log x)} :(0,\,e^{\frac{1}{e}}]\to(0,\,e]$
$y=e^{-W_{-1}(-\log x)} :(1,\,e^{\frac{1}{e}}]\to[e,\,\infty)$

$y=x^{x^y}$の概形

$y=x^{x^y}$は$y$については解けないが, $x$については解けるので, 逆関数を求めることでどんな関数で構成されるのか考えます.
$$ y=x^{x^y}\Leftrightarrow\log y=x^y \log x\Leftrightarrow y\log y=x^y \log x^y=(\log x^y)e^{\log x^y} $$
ランベルトの$W$関数を取ると
$$W((\log x^y)e^{\log x^y})=\log x^y=W(y\log y)\Leftrightarrow x=e^{\frac{W(y\log y)}{y}}$$

!FORMULA[83][-1309638227][0] $y=x^{x^y}$

$y=x^{x^y}$を構成する関数

$x=e^{\frac{W_0(y\log y)}{y}} :(0,\,e^{\frac{1}{e}}]\to(0,\,\infty)$
$x=e^{\frac{W_{-1}(y\log y)}{y}} :(0,\,\frac{1}{e}]\to(0,\,1]$

赤と青の曲線が交わる共有点は$(\frac{1}{e^e},\,\frac{1}{e})$です.

テトレーション関連の定理

$x^{x^{x^\cdots}}$が収束する実数$x$の範囲とその極限値

$x\in\mathbb{R}$のとき, $0< x\leq e^{\frac{1}{e}}$で収束し, その極限値は
$$ x^{x^{x^\cdots}}=e^{-W_0(-\log x)}=-\frac{W_0(-\log x)}{\log x} $$
である.

証明は前セクションから$W$関数を使った表示を得ているので, そこを参照してください. Wikipediaには代入する$x$が複素数の場合でも収束するものを選べば, この値に収束することが書かれていますが, 収束する条件が書いてませんでした. $0<|x|\leq e^{\frac{1}{e}}$らへんが妥当かな？

逆関数から導かれる無限テトレーションの値

$f(x)=x^{x^{x^\cdots}}\,(0< x\leq e^{\frac{1}{e}})$に対して
$$ f(x^{\dfrac{1}{x}})=x $$

定理1のきれいな値になるバージョンです.
$$ f(\sqrt{2})=\sqrt{2}^{\sqrt{2}^{\sqrt{2}^\cdots}}=2 $$
とかが有名なんじゃないですかね.

$y=f(x)$とすると, $y=x^y\Leftrightarrow \log y=y\log x\Leftrightarrow f^{-1}(y)=x=y^{\frac{1}{y}}$
前述より, $x^{\frac{1}{x}}$は$f$の逆関数となっている.
$$ \therefore f(x^{\frac{1}{x}})=f(f^{-1}(x)) $$
$y=f^{-1}(x)$とおくと, $y=f(x)$が収束する範囲に$x=f(y)$となる$x$を一つ取れる.
$$ \therefore f(x^{\frac{1}{x}})=f(f^{-1}(x))=f(y)=x $$