Sobolev不等式と等周不等式
解析学で有名なSobolev不等式と, 幾何学的な不等式の一種である等周不等式は同値なことが知られています. 今回はこのことを証明していこうと思います.
準備
今回は一般のRiemann多様体で考えるため, はじめに基本的な用語や証明に使う命題を準備しようと思います. Riemann多様体上には計量から導かれる自然な測度が存在しますので, 以下では特に断りがない限りその測度で考えます(通常の多様体と異なり, この測度は向き付け可能性に関係なく定義されます).
等周不等式
等周不等式は, 多様体の部分集合の表面積と体積に関する幾何学的な不等式です. 具体的には次のようなものを指します.
Riemann多様体$(M^m, g)$上で等周不等式が成立するとは, 次が成り立つことを言う:
ある定数$C>0$が存在して, 境界$\partial \Omega$がなめらかな$m-1$次元部分多様体となるような任意の相対コンパクト領域$\Omega \subset M$に対して,
\begin{align}
\vol{\Omega}^{\frac{m-1}{m}}\leq C\area{\partial \Omega}.
\end{align}
例えば$M=\mbb{R}^m$のときは, $C=\Gamma(m/2+1)^{1/m}/(m\sqrt{\pi})$として等周不等式が成り立ちます.
Riemann多様体上のSobolev空間
続いて, Sobolev不等式の定義を与えるのですが, その前にRiemann多様体上のSobolev空間について復習しておきます.
関数$u$に対し, $\nabla^k u$で$u$の$k$次共変微分を表すことにします($k=0$のときは, $\nabla^0 u=u$と約束することにします). 関数$u\in C_0^{\infty}(M)$のノルム$\|\cdot\|_{k, p}$を
\begin{align}
\|u\|_{k, p}^p=\sum_{j=0}^{k}\int_{M}|\nabla^k u|^p
\end{align}
で定義し, 関数空間$C_0^{\infty}(M)$のノルム$\|\cdot\|_{k, p}$に関する完備化を$W_0^{k,p}(M)$と表して, 今回はこれをRiemann多様体上のSobolev空間の定義とします.
このとき, $\mrm{Lip}_0(M)\subset W_0^{1, p}(M)$が任意の$p\geq 1$に対して成り立ちます. このことは実際, 局所座標近傍でlipschitz関数の台を被覆し, 通常のEuclid空間のときと同様の手順で局所的に近似したものを1の分割で貼り合わせ, なめらかな大域的近似を得ることによって示せます. 後の議論でも用いるのですが, 幾何学ではテスト関数としてしばしばlipschitz(区分的になめらか)なものを用いることが多いため, $\mrm{Lip}_0(M)$がSobolev空間に含まれていることは応用上大事な事実です.
Sobolev不等式とは, 関数空間のSobolev埋め込みに関する解析的な不等式の一種です.
Riemann多様体$(M^m, g)$上でSobolev不等式が成立するとは, 次が成り立つことを言う:
ある定数$C>0$が存在して, 任意の$u\in W_0^{1, m/(m-1)}(M)$に対して
\begin{align}
\left(\int_{M} |u|^{\frac{m}{m-1}}\right)^{\frac{m-1}{m}}\leq C\int_{M}|\nabla u|.
\end{align}
先程同様, $M=\mbb{R}^m$の時は, 等周不等式と同じ定数に対してSobolev不等式が成り立ちます.
一般にRiemann多様体上でこれらの不等式が必ずしも成立するとは限りませんが, 一方が成立すれば必ずもう一方の不等式も成立するという意味でこれらは同値な不等式です.
Riemann多様体$(M, g)$に対し, Sobolev不等式が成立することと, 等周不等式が成立することは同値である.
主張の証明
co-area公式
証明に必要なのは, 次のco-area公式と呼ばれる積分の変換公式です. この公式それ自体, 多様体上で解析学を行なう上で基本的かつ重要なツールの一つです.
$M^m$を$m$次元Riemann多様体とし, $h\in C^\infty(M)$をproperな非負関数とする. このとき, 任意の$f\in L^1(M)$と任意の$t>0$に対し,
\begin{align}
\int_{\{h\leq t\}} f\,|\nabla h|=\int_{0}^{t} \int_{\{h=\tau\}}f\, d\tau
\end{align}
が成り立つ. ここで, 右辺の積分$\int_{\{h=\tau\}}f$は, $m-1$次元Hausdorff測度に関する積分とする.
実は$h$をLipschitz関数としても主張が成立することが知られています. このことはLusinの定理の$C^1$版と呼ぶべきものを用いて, なめらかな場合に帰着させることで示せるのですが, その命題の証明にWhitneyの拡張定理という大道具が必要になります. 少し大変なので詳細は幾何学的測度論の本に譲り, ここでは扱わないことにします.
はじめに, $M'=\{x\in M|\nabla h \neq0\}$とおくと, $M'$は$M$の開集合であり, また, Sardの定理により, $\mbb{R}$における$h$の特異値全体の成す集合は測度$0$となるから,
\begin{align}
\int_{\{h\leq t\}\cap M'} f\,|\nabla h|=\int_{0}^{t} \int_{\{h=\tau\}\cap M'}f\, d\tau
\end{align}
を示せばよい. $M'=\emptyset$の時は主張の成立は明らかだから, 以下$M'\neq\emptyset$とする.
任意の$x_0\in M'$を取り, $h(x_0)=t_0$とする. $h$の正則値全体の成す集合は$\mbb{R}$の開集合となるから, 十分小さな$\eps_0>0$を取れば, $|t_0-\tau|<\eps_0$を満たす任意の$\tau$に対し, 集合$\Sigma_\tau=h^{-1}(\tau)$は$M'$のコンパクトな$(m-1)$次元部分多様体となる.
$I=(t_0-\eps_0, t_0+\eps_0)$とおき, 集合$h^{-1}(I)$上のベクトル場$X= \nabla h/|\nabla h|^2$を考える. 集合$h^{-1}(I)$上では$\nabla h\neq 0$となるため, この上で$X$はなめらかなベクトル場を定める. そこで, $\phi_{\tau-t_0}$を$X$が生成するflow, すなわち微分同相の一径数族で
\begin{align}
\frac{d}{d\tau}\phi_{\tau-t_0}(p)=X_p, \quad \phi_0(p)=p, \quad \text{for any $p \in h^{-1}(I)$}
\end{align}
を満たすものとし, 写像$\Phi: \Sigma_{t_0}\times I \to h^{-1}(I)$を$\Phi(p. \tau)=\phi_{\tau-t_0}(p)$で定めると, $\Phi$は$h^{-1}(I)$への微分同相になる.
任意の$(p, \tau)\in \Sigma_{t_0}\times I$に対し,
\begin{align}
h(\Phi(p, t_0))&=h(\phi_0(p))=h(p)=t_0, \\
\frac{d}{d\tau}h(\Phi(p, \tau))&=dh_{\Phi(p, \tau)}\left(\frac{d}{d\tau} \phi_{\tau-t_0}(p)\right)=\inn{\nabla h}{\frac{\nabla h}{|\nabla h|^2}}_{\Phi(p. \tau)}=1
\end{align}
となるため, 平均値の定理により$h(\Phi(p. \tau))=\tau$となる. よって$\Phi(p, \tau)\in \Sigma_{\tau}$.
さらに, $\nabla h \perp \Sigma_{\tau}$より$\Phi_{\tau} \perp \Sigma_{\tau}$である.
点$(p, \tau)\in h^{-1}(I)$, $p\in \Sigma_{\tau}$の周りの局所座標近傍として$(h^{-1}(I), \Phi^{-1})$を考えることにし, $G(\tau)$を$\Sigma_{\tau}$上の計量とすると, 計量$g$の局所表示は
\begin{align}
g=
\begin{pmatrix}
G(\tau) & 0\\
0 & \frac{1}{|\nabla h|^2}
\end{pmatrix}
\end{align}
で与えられる. よって, 体積要素$d\mu$の局所表示は
\begin{align}
d\mu &= \sqrt{\det{g}}\,dx^1\cdots dx^{m-1} d\tau \\
&= \frac{1}{|\nabla h|}\sqrt{\det{G(\tau)}}\,dx^1\cdots dx^{m-1} d\tau \\
&= \frac{1}{|\nabla h|}d\mrm{Area}(\tau)\, d\tau
\end{align}
となるので, 任意の$f\in L^1(M)$に対して,
\begin{align}
\int_{M}f|\nabla h|=\int_{0}^{t}\int_{\Sigma_{\tau}}f\, d\tau.
\end{align}
Sobolev不等式 $\Rightarrow$ 等周不等式
比較的簡単な方から示します.
$\Omega$をなめらかな境界を持つ相対コンパクト領域とし, 十分小さな$\eps>0$に対して
\begin{align}
\Omega_\eps=\{x \in \Omega|\, \mrm{dist}(x, \partial \Omega)>\eps\}
\end{align}
とおきます. 関数$u$を
\begin{align}
u=
\begin{cases}
1 &\text{on $\Omega_\eps$,}\\
\eps^{-1}\mrm{dist}(x, \partial \Omega) &\text{on $\Omega \setminus \Omega_\eps$,}\\
0 &\text{outside of $\Omega$,}
\end{cases}
\end{align}
で定義します. このとき, $u\in \mrm{Lip}_0(M)$および$|\nabla u|\leq \eps^{-1}$を満たすので, Sobolev不等式より,
\begin{align}
\vol{\Omega_\eps}^{\frac{m-1}{m}}\leq \left(\int_{M}u^{\frac{m}{m-1}}\right)^{\frac{m-1}{m}}\leq C\int_{M}|\nabla u|\leq C\eps^{-1}\vol{\Omega\setminus \Omega_\eps}
\end{align}
となります. ここで, co-area公式を使うと, 最右辺は
\begin{align}
\vol{\Omega\setminus \Omega_\eps}=\int_{\mrm{dist}(\cdot, \partial \Omega)\leq \eps} 1=\int_{0}^{\eps}\area{\{x\in\Omega|\, \mrm{dist}(x, \partial \Omega)=\eps\}}
\end{align}
と計算できます. 以上の式で$\eps \to 0$とすると, 左辺は優収束定理より
\begin{align}
\vol{\Omega_\eps}^{\frac{m-1}{m}}\to\vol{\Omega}^{\frac{m-1}{m}},
\end{align}
右辺は微分積分学の基本定理から
\begin{align}
\eps^{-1}\int_{0}^{\eps}\area{\{x\in\Omega|\, \mrm{dist}(x, \partial \Omega)=\eps\}}\to \area{\partial\Omega}
\end{align}
となるので, 等周不等式
\begin{align}
\vol{\Omega}^{\frac{m-1}{m}}\leq C\area{\partial \Omega}
\end{align}
が成り立つことがわかりました.
等周不等式 $\Rightarrow$ Sobolev不等式
続いて, 逆向きの条件を示します.
任意の非負な$u\in C_0^{\infty}(M)$に対し不等式を示せればOKです. 等周不等式とco-area公式より
\begin{align}
\int_{M}|\nabla u| &= \int_{0}^{\infty}\area{\{u=t\}}dt\\
&\geq C^{-1}\int_{0}^{\infty}\vol{u\geq t}^{\frac{m-1}{m}}dt
\end{align}
となります. 右辺を変形するため, 次の事実を用います.
$(X, \mu)$を測度空間とすると, 任意の関数$f\in L^1(X)$および任意の$p>0$に対し,
\begin{align}
\int_{X}|f|^p d\mu=p\int_{0}^{\infty}t^{p-1}\mu(\{|f|\geq t\})dt.
\end{align}
左辺は
\begin{align}
\int_{X}|f|^p d\mu = p\int_{X}\int_{0}^{|f(x)|}t^{p-1}dtd\mu(x)=p\int_{X}\int_{0}^{\infty}\chi_{|f|\geq t}(x)t^{p-1}dtd\mu(x)
\end{align}
と変形できるから, 最右辺にFubiniの定理を適用して
\begin{align}
\int_{X}|f|^p d\mu=p\int_{0}^{\infty}t^{p-1}\int_{X}\chi_{|f|\geq t}(x)d\mu(x)dt = p\int_{0}^{\infty}t^{p-1}\mu(\{|f|\geq t\})dt.
\end{align}
補題3より,
\begin{align}
\left(\int_{M}u^{\frac{m}{m-1}}\right)^{\frac{m-1}{m}}
&= \left(\int_{0}^{\infty}\frac{m}{m-1}t^{\frac{1}{m-1}}\vol{\{u\geq t\}}dt\right)^{\frac{m-1}{m}}\\
&= \left(\int_{0}^{\infty}\frac{m}{m-1}\vol{\{u\geq t\}}^{\frac{m-1}{m}}\, \vol{\{u\geq t\}}^{\frac{1}{m}}t^{\frac{1}{m-1}}dt\right)^{\frac{m-1}{m}}\\
&= \left(\int_{0}^{\infty}\frac{m}{m-1}\vol{\{u\geq t\}}^{\frac{m-1}{m}}\, (t\vol{\{u\geq t\}}^{\frac{m-1}{m}})^{\frac{1}{m-1}}dt\right)^{\frac{m-1}{m}}
\end{align}
となります. ここで, $t\mapsto \vol{\{u\geq t\}}$が非増加関数であることに注意すると, 不等式
\begin{align}
t\vol{\{u\geq t\}}^{\frac{m-1}{m}} \leq \int_{0}^{t}\vol{\{u\geq s\}}^{\frac{m-1}{m}}ds
\end{align}
を得ますから,
\begin{align}
\left(\int_{M}u^{\frac{m}{m-1}}\right)^{\frac{m-1}{m}}
&=\left(\int_{0}^{\infty}\frac{m}{m-1}\vol{\{u\geq t\}}^{\frac{m-1}{m}}\, (t\vol{\{u\geq t\}}^{\frac{m-1}{m}})^{\frac{1}{m-1}}dt\right)^{\frac{m-1}{m}}\\
&\leq \left(\int_{0}^{\infty}\frac{m}{m-1}\vol{\{u\geq t\}}^{\frac{m-1}{m}}\, \left(\int_{0}^{t}\vol{\{u\geq s\}}^{\frac{m-1}{m}}ds\right)^{\frac{1}{m-1}}dt\right)^{\frac{m-1}{m}}.
\end{align}
ここで, $F(t)=\int_{0}^{t}\vol{\{u\geq s\}}^{(m-1)/m}ds$とおくと,
\begin{align}
\left(\int_{M}u^{\frac{m}{m-1}}\right)^{\frac{m-1}{m}}
&\leq \left(\int_{0}^{\infty}\frac{m}{m-1}F(t)^{\frac{1}{m-1}}F'(t)dt\right)^{\frac{m-1}{m}}\\
&=F(\infty)=\int_{0}^{\infty}\vol{\{u\geq s\}}^{\frac{m-1}{m}}ds\\
&\leq C \int_{0}^{\infty}\area{\{u=t\}}dt\\
&= C\int_{M}|\nabla u|
\end{align}
と計算され, これによりSobolev不等式の成立が分かります.
以上によって, めでたく等周不等式とSobolev不等式の同値性が示されました.
不等式が成り立たない例
最後に, 等周不等式およびSobolev不等式が成り立たないRiemann多様体の例を見てみましょう.
関数$y=1/x\,(x>0)$のグラフを$x$軸の周りに1回転させてできる曲面を$M$とし, $M$には$\mbb{R}^3$から誘導される計量を入れてRiemann多様体とみなしておく. 任意の実数$a>1$を取り, この曲面の$1 \leq x \leq a$の部分を考える. $a$を大きくすると面積は無限大に発散するのに対し, 境界の長さはある一定の値に収束するため, 等周不等式は成立しない.
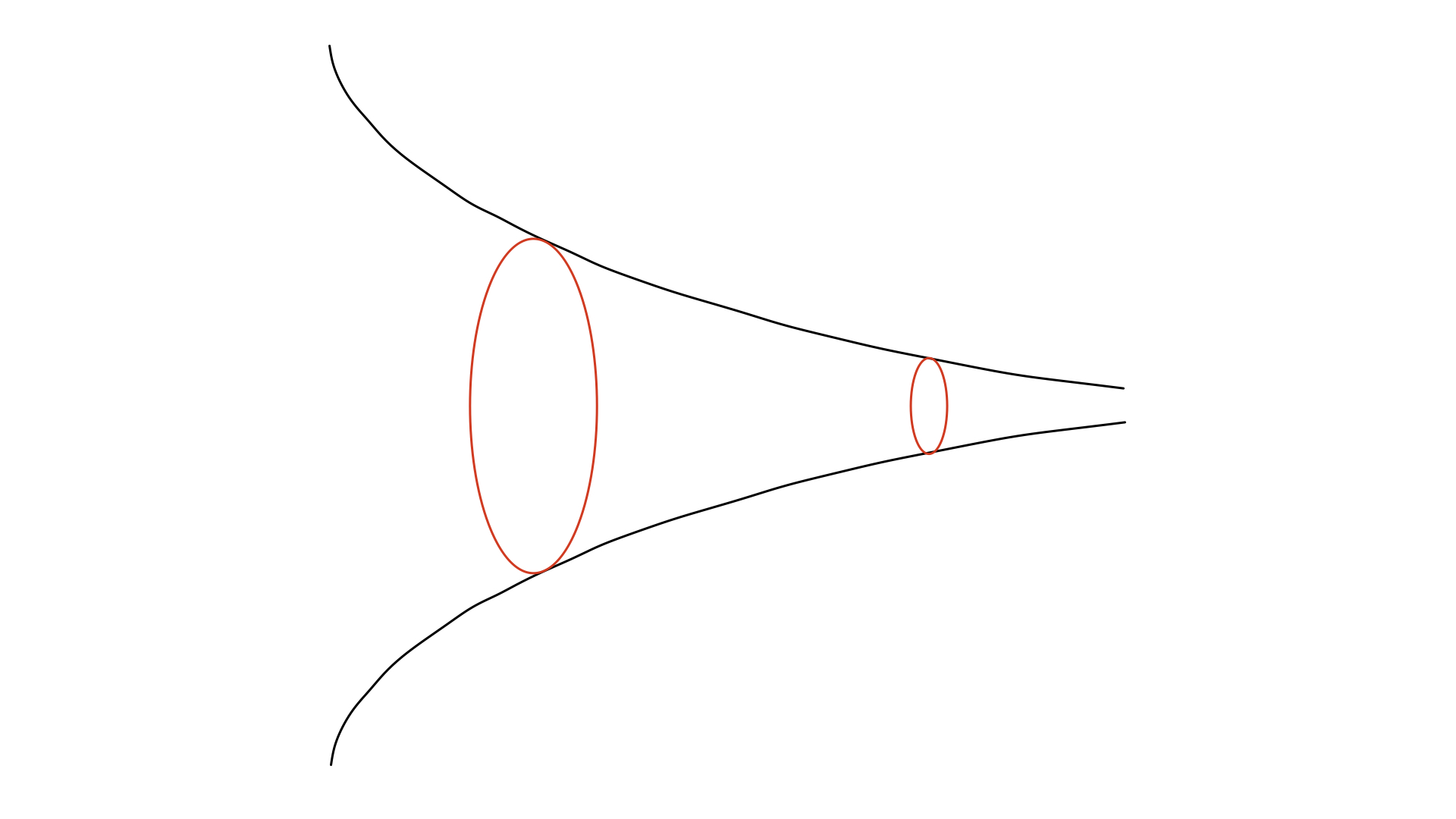Gabrielのラッパの概形
Gabrielのラッパはその形状からも分かる通りカスプ状の構造をしており, これが等周不等式の成立を妨げています. 逆に, カスプを有さないと考えられる条件下では, (局所的に)等周不等式が成立することが示せます.
おわりに
今回はSobolev不等式と等周不等式の同値性を示し, これらの不等式が成り立たない例を見ました. コンパクトでないRiemann多様体上でこれらの不等式が成り立つかどうかは, Sobolev埋め込みの成立の可否に関わるため, それ自体重要な問題でもあります. どのような条件下で成立するか等の詳細はHeが詳しいです.
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
