プライバシー重視の村人と,出来るだけ監視したい村長(円周点配置に対する距離積のミニマックス問題)
本記事では以下のような最適化問題を考えます.
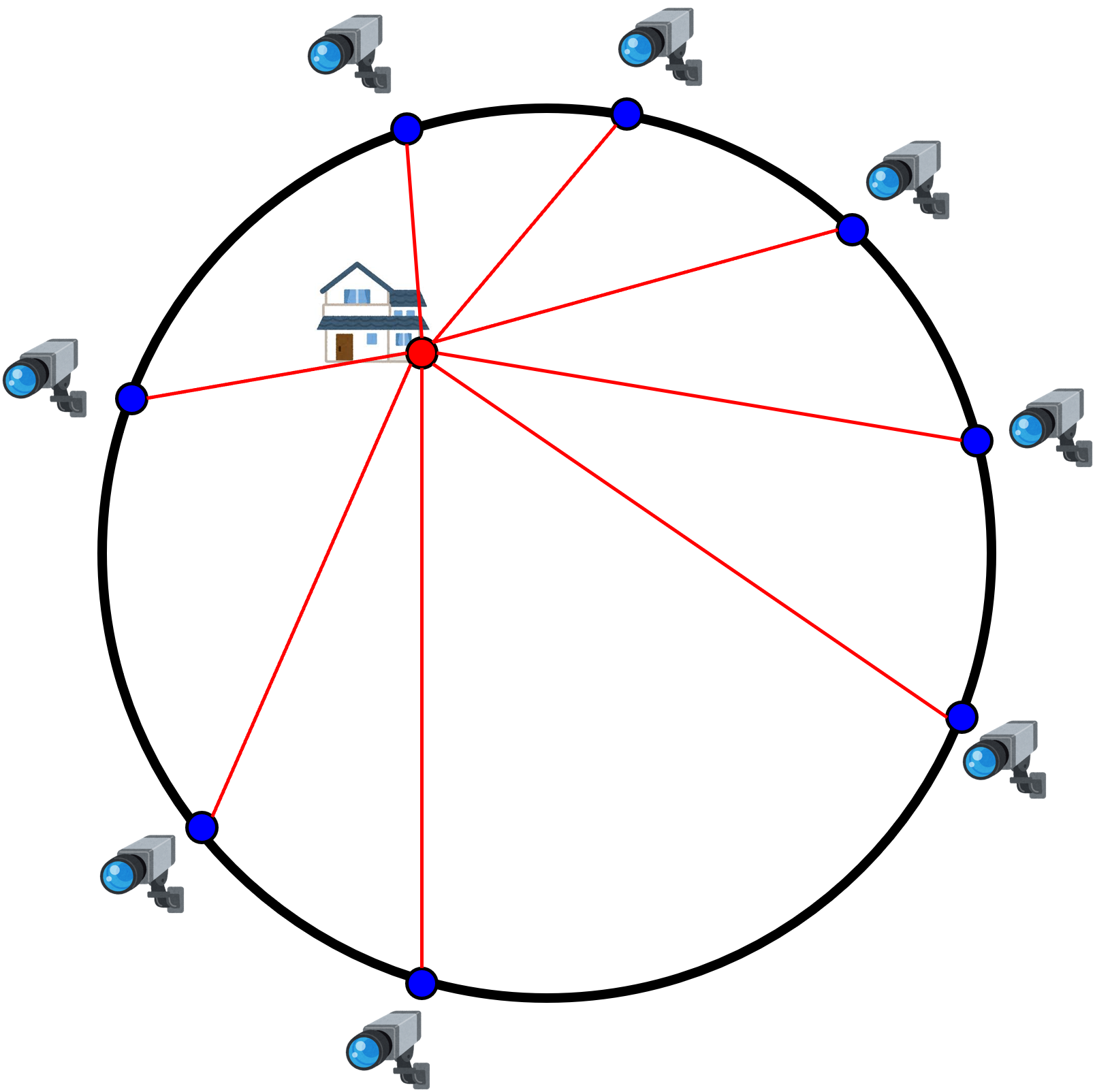
半径$1$の円形の村があります.村長は村の周囲(円周)に,有限個の監視カメラを設置する予定です.
監視カメラが全て設置された後,とある男性が村の内部または円周の好きな場所に家を建てるつもりです.
監視カメラが遠ければ遠いほど映像がぼやけるため,男性は家から各監視カメラまでの距離を全て掛け合わせた値が大きくなるほどプライバシーが守られると考え,その値が最大になる場所を選びます.
(この最大値をプライバシー指数と呼ぶことにします.)
一方,村長は監視を効かせたいので,プライバシー指数が出来る限り小さくなるように監視カメラをあらかじめ設置しておきたいです.(男性が家を建てた後は監視カメラの配置は変えられないものとします.)
村長は監視カメラをどのように設置すれば良いでしょうか?
この問題の答えとして,次の命題が成立します.
$B:= \{(x,y) \in \mathbb{R}^2 \mid \|(x,y)\|^2_{\mathbb{R}^2}:=x^2 + y^2 \leq 1 \}$として,その境界を$\partial B$としたとき,
$$ \displaystyle \min_{\substack{Q \subset \partial B, \\ \# Q < \infty} } \max_{p \in B} \prod_{q \in Q} \|p - q \|_{\mathbb{R}^2} =2$$となり,任意の自然数$N$に対して,
$$\left\{ \left(\cos \frac{2\pi j}{N}, \sin \frac{2\pi j}{N} \right) \right\}_{j=1}^{N} \in \displaystyle \underset{\substack{Q \subset \partial B, \\ \# Q < \infty}} {\operatorname{argmin}} \max_{p \in B} \prod_{q \in Q} \|p - q \|_{\mathbb{R}^2}$$
が成立する.したがってプライバシー指数は,監視カメラを正多角形の頂点上に設置すると最小値$2$を達成する.
それでは以下の3Stepでこの命題を証明していきましょう.
Step 1: 複素平面で考え,実は家が円周上に建つことを示す
単位円における距離の積を扱う場合,複素平面で考える方が扱いやすい.そこで改めて,$\mathbb{C}$上の単位閉円板を$B~(:= \{z \in \mathbb{C} \mid |z| \leq 1 \})$,その境界を$\partial B~(=\{z \in \mathbb{C} \mid |z| = 1 \})$とする.
$Q:=\{z_1, \ldots ,z_N\} \subset \partial B$に対して,$\displaystyle P(z;Q) := \prod_{k=1}^N (z - z_k)$とおく.各有限集合$Q$に対して,$P(z;Q)$は$\mathbb{C}$上正則であるため,以下の最大絶対値の原理から,$\displaystyle \max_{z \in B} |P(z;Q)| = \max_{z \in \partial B} |P(z;Q)|$が成立する.
$D \subset \mathbb{C}$を連結な開集合として,正則な複素関数$f:D \to \mathbb{C}$に対して以下が成り立つ.
・$|f(z)|$の最大値を$D$の内部で取る場合,$f$は定数関数となる.
・系として,コンパクト部分集合$K\subset D$に対して,$\partial K$をその境界とすると,
$$ \displaystyle \max_{z \in K} |f(z)| = \max_{z \in \partial K} |f(z)|$$
となる.
(この定理の証明は例えば
Wikipedia
に載ってるいるのでご参照ください.)
したがって,
$$ \displaystyle \min_{\substack{Q \subset \partial B, \\ \# Q < \infty} } \max_{z \in \partial B} |P(z; Q)| =2,$$
$$\left\{ e^{\frac{2\pi i}{N} j}\right\}_{j=1}^{N} \in \displaystyle \underset{\substack{Q \subset \partial B, \\ \# Q < \infty}} {\operatorname{argmin}} \max_{z \in \partial B} |P(z; Q)| $$
を示せばよい.
Step 2: プライバシー指数$\geq 2$の証明
次に,$\partial B$の任意の有限部分集合$Q \subset \partial B$に対して,$\displaystyle \max_{z\in \partial B} |P(z;Q)| \geq 2$を示す.
ここで,$Q=\{z_1, \ldots ,z_N\}$として,距離関係は全体を回転させても変わらないため,$\displaystyle (-1)^N \prod_{k=1}^N z_k = 1$を仮定しても問題ない.
実際,$Q = \{w_1, \ldots ,w_N\} \subset \partial B$に対して, $\displaystyle \alpha := - \prod_{k=1}^N \overline{w_k}^{1/N} \in \partial B$として,$\alpha Q = \{z_1,\ldots , z_N\} := \{\alpha w_1, \ldots ,\alpha w_N\}$とすると,$|P(z; Q)| = |P(\alpha z; \alpha Q)|$であり,
\begin{align*}\displaystyle
(-1)^N \prod_{k=1}^N z_k &= (-1)^N \alpha^N \prod_{k=1}^N w_k = 1
\end{align*}を満たす.ここで,$s_l$を$ z_1, \ldots ,z_N$からなる$l$次基本対称式とすると,上の仮定から,
\begin{align*}
P(z; Q) &= z^N -s_1 z^{N-1} + s_2 z^{N-2} - \cdots +1
\end{align*}
となる.また,$\displaystyle \zeta_j := e^{\frac{2\pi i}{N} j}$とおくと,
\begin{align*}\displaystyle
\sum_{j=1}^N \zeta_j^k = \begin{cases} N & \text{if $k=N$,} \\ 0 & \text{if $1 \leq k \leq N-1$} \end{cases}
\end{align*}が成り立つことに注意すれば,
\begin{align*}
\sum_{j=1}^N P(\zeta_j; Q) &= \sum_{j=1}^N (\zeta_j^N -s_1 \zeta_j^{N-1} + s_2 \zeta_j^{N-2} - \cdots +1)\\
&=\sum_{j=1}^N \zeta_j^N- s_1\sum_{j=1}^N \zeta_j^{N-1} + s_2 \sum_{j=1}^N \zeta_j^{N-2} -\ldots + \sum_{j=1}^N 1\\
&=\sum_{j=1}^N \zeta_j^N + \sum_{j=1}^N 1 = 2N
\end{align*}となる.よって,\begin{equation}
\frac{1}{N}\sum_{j=1}^N |P(\zeta_j; Q)| \geq \frac{1}{N} \left|\sum_{j=1}^N P(\zeta_j; Q) \right| =2
\end{equation}となり,少なくとも一つある$j \in \{1,\ldots, N\}$が存在して,$|P(\zeta_j; Q)| \geq 2$となる.
したがって$\displaystyle \max_{z\in \partial B} |P(z; Q)| \geq 2$が示された.
Step 3: 等号が成立する$Q$の存在証明
最後に,ある有限部分集合$Q \subset \partial B$が存在して,$\displaystyle \max_{z\in \partial B} |P(z; Q)| = 2$となることを示す.
自然数$N$に対して,$\displaystyle \eta_j:= e^{(2j+1)\frac{ \pi i}{N}}$とおく.
ここで,$Q:=\{\eta_1,\ldots ,\eta_N \} \subset \partial B$とすると,$Q$は$z^N +1$の根からなる集合のため,
$ \displaystyle P(z; Q) = \prod_{j=1}^N (z - \eta_j) = z^N + 1$となる.よって,任意の$z \in \partial B$に対して,
\begin{align*}\displaystyle
|P(z; Q)| &= |z^N + 1| \\
&\leq |z|^N + 1 \\
&=2
\end{align*}であり,$z :=1 \in \partial B$とおけば,$|P(z; Q)|=2 $より,$\displaystyle \max_{z\in \partial B} |P(z; Q)| = 2$が示された.
よって,Step 2と合わせて
$$ \displaystyle \min_{\substack{Q \subset \partial B, \\ \# Q < \infty}} \max_{z \in \partial B} |P(z; Q)| = 2$$となる.また,$Q=\{\eta_1,\ldots ,\eta_N \}$を回転させれば,$\displaystyle \left\{ e^{\frac{2\pi i}{N} j}\right\}_{j=1}^{N} \in \underset{\substack{Q \subset \partial B, \\ \# Q < \infty}} {\operatorname{argmin}} \max_{z \in \partial B} |P(z; Q)|$も得られる.
まとめ
以上よりプライバシー指数を最小にしたい場合,村長は村の周囲である円周上に等間隔で監視カメラを置けばよいということが分かりました.しかし,この証明から分かる通り,最小値は監視カメラの個数$N$に依存しません.どんな個数であろうとも必ずプライバシー指数の最小値は$2$です.例えば監視カメラが$1$個の場合でも,カメラの真反対の円周上に家を建てることで距離の最大値$2$を達成します.カメラを増やしても数値は改善しません.こうした性質から,そもそも「プライバシーが守られる」という妥当な定義は何なのか?という問題を(例えば総和や平均,リースポテンシャルなど,あるいは個数に対するコストなどを)別途考察する必要がありそうです.(ぶっちゃけると今回の問題設定は複素関数を使って綺麗に解けるので紹介しました.暇があればまた今度記事にするかも?)