コラッツ予想について考えたこと（後編）

前回はコラッツ予想の一般化を試みました。
今回はコラッツ予想そのものについて考えたことを書きます。
前編は こちら

概要

コラッツ数列と収束性やループの有無が同値であるような別の数列を作成し、考察しました。特に得るものはありませんでしたが記録しておきます。

コラッツ数列

一般的な名称かわかりませんが「コラッツ数列」を以下で定義します。
$$\mathrm{\forall }{a}_n\in \mathbb{N}\text{に対し}$$
$$a_{n+1}=\begin{array}{r}\{\begin{array}{l}{a}_n/2\text{if}{a}_n\equiv 0\mathrm{mod}2\\ (3a_n+1)/2\text{otherwise}\end{array}\end{array}$$

別の数列に変換してみます

コラッツ数列において偶数はスキップしてかまわない（コラッツ予想の成立可否には影響ない）ので奇数のみ考えます。

例えば
$3\to 10\to 5\to 8\to 4\to 2\to 1$
は
$3\to 5\to 1$
と考えても、コラッツ予想の主張は変わりません。

さて、奇数$n$は $4n+1$ と行先が同じになります。
どういうことかというと、例えば3と13は
$3\to 5\to 1$
$13\to 3\to 5\to 1$
となり、途中で合流するということです。

なぜならば $n$ は奇数なので $4n+1$ も奇数となり
$$4n+1\to \frac{3(4n+1)+1}{2}=6n+2\to 3n+1$$
これは偶数なので
$$3n+1\to \frac{3n+1}{2}$$
結局 $4n+1\to \frac{3n+1}{2}$ となり、$n$ の行先と一致するからです。

従って、コラッツ予想を考える上では、$4n+1$ を繰り返し適用して得られる数たちは同一視でき、代表として一つの奇数のみ考えればよいことになります。
例えば$3,13,53,213$ などは $5$ に行きつくので、$5$についてのみ予想が成立するか考えれば良いことになります。

表にすると以下のようになります。一番左の数が代表の数です。

話が前後しますが、表は以下のルールで生成します。

まず、$1$を起点として $4n+1$ を繰り返し、1行目を作ります。
$1,5,21,85,\cdots$ と続きます。

次に、ここに現れない最小の奇数を取り、同様に $4n+1$ を繰り返します。
$3,13,53,\cdots$ となります。

同じように、ここまでに現れない最小の奇数をとって $4n+1$ を繰り返します。

この操作の各段階で現れる「最小の奇数」は
「奇数$n$ を用いて $4n+1$ と表されない数」
すなわち
「$2s+1\text{(sは奇数)}$」 あるいは「$4t+1\text{(tは偶数)}$」
です。
$1,3,7,9,11,15,17,19,\cdots$と続きます。（表の2列目）

これらに対し、コラッツ数列の行先(偶数をスキップしたもの)を代表数として対応させます。
$3\to 5,7\to 11,9\to 7,11\to 17,\cdots$
さらに代表数でソートしたものが上の表となります。

作り方から明らかなように、表にはすべての奇数が現れます。

さて、コラッツ数列の収束性、ループの有無を考えるとき、2列目以降は重要ではありません。結局1列目に行きつくので、重要なのは「どの行に移動するか」です。

というわけで行に番号を振ります。

そして、コラッツ数列のふるまいを行番号で置き換えます。
例えば、11から始まるコラッツ数列（の偶数を省略したもの）
$11\to 17\to 13\to 3\to 5\to 1$
は、行番号で置き換えると
$6\to 5\to 2\to 1$
となります。

ここで改めて、代表数から行番号への変換方法を記述しておきます。

要は、代表数を3で割って切り上げると行番号になるという事です。

今後はこの、行番号に変換した後の数列について考えます。名前がないと不便なので「新数列」と呼ぶことにします。

コラッツ予想の言い換え

早速ですがここで、新数列を逆にたどることを考えてみます。
$1\to 2\to 5\to 6\to \cdots$
この数列を「逆新数列」と名付けます。

1に収束する新数列は無数にあるので、1から始まる逆新数列も無数にあります。
例えば
$1\to 29\to 38\to \cdots$
$1\to 114\to 76\to 51\to \cdots$
などです。
数列というよりツリーと言った方が分かりやすいかもしれません。
図にするとこんなツリーです。
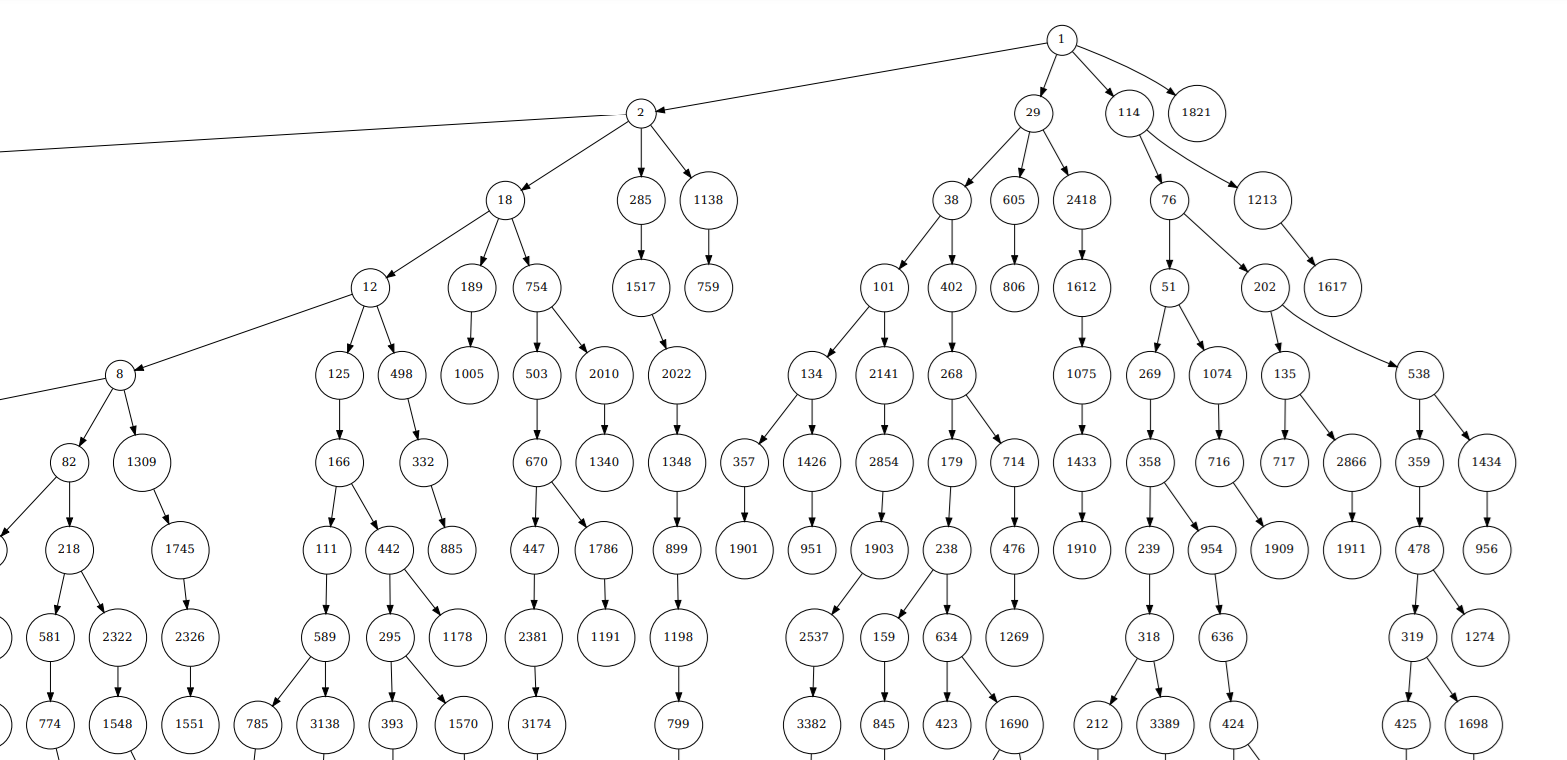逆新数列のツリー

省いていますが右にも下にも無限に続きます。一つの数から無限に枝分かれしています。

コラッツ予想の主張は、「1から始まる逆新数列にすべての自然数が現れる」すなわちこのツリー上にすべての自然数が現れることと同値です。

逆新数列はどのように生成されるでしょうか。

天下り的ですが、ツリーの親子には以下の関係があります。

また、各要素からはいくつもの子要素が枝分かれします。最小の子要素は上のルールで生成されますが、「兄弟」は以下の規則で生成されます。

例えば、

$1\to 2\to 5\to 6\to \cdots$
$1\to 29\to 38\to \cdots$
$1\to 114\to 76\to 51\to \cdots$

を見ると、$2$と$29$は$1$を親とした兄弟です。

$2\equiv 0\mathrm{mod}2$なので$2$の兄は
$2\times 16-3=29$
で$29$となっていることが分かります。

そのまた兄は
$29\times 4-2=114$
となっていることが確認できます。

このあたりの生成ルールは、元のコラッツ数列にさかのぼって考えれば簡単に証明できます。

いろいろ考察します

ツリーの生成規則は少しややこしいので、行列で書き直します。
例えば
$$m=\frac{16n-9}{3}$$
は
$$\left(\begin{array}{c}m\\ 1\end{array}\right)=3^{-1}\left(\begin{array}{cc}{2}^4& -3^2\\ 0& 3\end{array}\right)\left(\begin{array}{c}n\\ 1\end{array}\right)$$
と表せます。

同じように書き換えると、命題1(ツリー生成規則)は以下になります。

分かりやすくなったのか微妙なところですが、兄弟規則の方も書き換えてみます。

というわけで、コラッツ予想は以下と同値となります。

いよいよ自分でも何をやっているか分からなくなってきたので、もとのコラッツ数列に立ち返って計算してみます。

例

$177$から始まるコラッツ数列を考えます。偶数は省いてあります。
$177,133,25,19,29,11,17,13,5,1$

step1. 代表数だけにする
$177=4\times 44+1$なので、「最小の数」となっています。（$44$が偶数なので）
したがって次の$133$が「代表数」です。
この調子で代表数だけ残して後は省きます。

$133,25,19,29,11,17,13,5,1$
となりました。

step2. 新数列に変換する
各数を行番号に変換して、新数列を作ります。行番号への変換は「3で割って切り上げる」です。

$45,9,7,10,4,6,5,2,1$

step3. 逆順にして行列の積で表す
まず逆新数列にします。（逆に並べただけです）
$1,2,5,6,4,10,7,9,45$

$4\to 10$の部分は、$10$が兄弟の形式になっていますので
$4\to 3\to 10$
となります。

先頭の$1$は省いて$2$から先を考えると、結局こうなります。

$2,5,6,4,3,10,7,9,45$

生成規則どおりに書くと

$$A_3\cdot A_1\cdot A_4\cdot B_1\cdot A_4\cdot A_0\cdot A_5\cdot A_2\left(\begin{array}{c}2\\ 1\end{array}\right)$$
これが
$$\left(\begin{array}{c}45\\ 1\end{array}\right)$$
になっているはずです。

気合を入れて下記の積を計算すると
$$\begin{array}{rcl}S& =& 3^{-7}\left(\begin{array}{cc}{2}^4& -3^2\\ 0& 3\end{array}\right)\cdot \left(\begin{array}{cc}{2}^2& -1\\ 0& 3\end{array}\right)\cdot \left(\begin{array}{cc}2& 1\\ 0& 3\end{array}\right)\cdot \left(\begin{array}{cc}{2}^2& -2\\ 0& 1\end{array}\right)\left(\begin{array}{cc}2& 1\\ 0& 3\end{array}\right)\cdot \left(\begin{array}{cc}2& 0\\ 0& 3\end{array}\right)\cdot \left(\begin{array}{cc}{2}^2& -2\\ 0& 3\end{array}\right)\cdot \left(\begin{array}{cc}{2}^3& -1\\ 0& 3\end{array}\right)\\ & =& 3^{-7}\left(\begin{array}{cc}{2}^{16}& -2^{13}-2^{12}\cdot 3+2^9\cdot 3^3-2^8\cdot 3^4+2^6\cdot 3^4-2^4\cdot 3^5-3^8\\ 0& 1\end{array}\right)\end{array}$$
となり

$$\begin{array}{r}S\left(\begin{array}{c}2\\ 1\end{array}\right)=\left(\begin{array}{c}45\\ 1\end{array}\right)\end{array}$$
になっていることが確認できます。

ツリー上で示すと下記のような動きです。
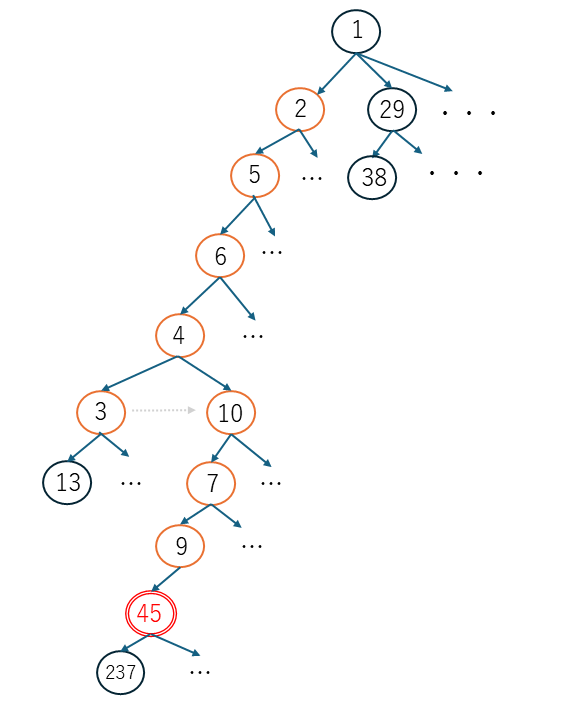例

行列の形式

$A_i,B_i$の形から、その積Sは

$$\begin{array}{r}S=3^{-d}\left(\begin{array}{cc}{2}^k& \sum _{i,j\in \mathbb{N}}(\pm 2^i\cdot 3^j)\\ 0& 1\end{array}\right)\end{array}$$
といった形になります。（書き方が間違っているかもしれませんが、通じますかね…）
したがって
$$\begin{array}{r}S\left(\begin{array}{c}2\\ 1\end{array}\right)=\left(\begin{array}{c}m\\ 1\end{array}\right)\end{array}$$
としたとき
$m=3^{-d}\{2^l+\sum _{i,j\in \mathbb{N}}(\pm 2^i\cdot 3^j)\}$
です。

すべての自然数がこの形になる、というのがコラッツ予想の言っていることだと思います。
（添え字は上述の「生成規則」で決まるので、結構強い制限があります）

でも結局、この結論は「新数列」など持ち出さなくても元のコラッツ予想から直接導き出せそうな気もします…。

コラッツ予想が成立しないとどうなるのか

コラッツ予想が成立しないと仮定すると、1から始まるツリーには現れない数が存在することになります。
そのような数たちは、また別のツリー（のようなもの）を形成しています。

ループをなす数列の場合は、対応するツリーは同じパターンを繰り返すものになります。
ループではなく異なる数が続いて収束しない場合、ツリーは上下に広がる形になります。

行列でいうと、ループをなす場合は

$$\begin{array}{r}\mathrm{\exists }m\in \mathbb{N};\left(\begin{array}{c}m\\ 1\end{array}\right)=S\left(\begin{array}{c}m\\ 1\end{array}\right)\end{array}$$
これを解くと
$$\begin{array}{r}m=\frac{\sum _{i,j\in \mathbb{N}}(\pm 2^i\cdot 3^j)}{3^d-2^l}\end{array}$$
です。

添え字の条件を丁寧に見ていけば$m$の満たすべき条件などが言えるかもしれません。（力尽きたのでやっていません）

ループをなさず、異なる数が続く場合は

$$\begin{array}{r}\mathrm{\forall }s\mathrm{\exists }n>s;\left(\begin{array}{c}n\\ 1\end{array}\right)=S\left(\begin{array}{c}m\\ 1\end{array}\right)\text{となる}m\text{が存在する。}\end{array}$$
でしょうか。
つまり、ある$m$（収束しない数）に対しては、いくらでも大きい数からツリーを始めることができるということです。

まとめ

書き始めたものの説明するのが難しくて後半は伝わりにくいかもしれません。
新しい数列、などと書いていますが、コラッツ数列を要約して変換しただけなので本質的には何も新しいことはしてません。

今回ちょっと考えてみただけですが「なるほど難しいな」という事がよくわかりました。
それだけでも十分楽しめたものの、もう少し数学の知識があればより楽しいんだろうなと痛感しました。