major indexによるq-二項係数
正方格子路にmajor indexと呼ばれる統計量を定義し，それに関する母関数が$q$-二項係数になることを示す．
本記事の元ネタの文献 [1]によると，これはもともと
MacMahon
の仕事らしい．
\begin{align}
\sum_{\omega\in L(n,r)}q^{{\rm maj}(\omega)}=
\binom{n+r}{r}_q
\end{align}
但し$L(n,r)$は$(0,0)$から$(n,r)$まで，ステップ$(1,0)$と$(0,1)$を使って行くパス (注：そういうのを正方格子路という)．
元ネタ文献 [1]の練習問題6.4では，$\textrm{area}(\omega)=k$な正方格子路$\omega$を$\textrm{maj}(\omega')=k$な正方格子路$\omega'$にうつす全単射を構成して示してたが，以下では趣を変えてパスカルの三角形を経由して示してみる．
ちなみに，統計量$\textrm{maj}$の面白いところは，正方格子路の特殊な場合であるDyck路を$\textrm{maj}$で数えると，以下のように積で書けるところである [1, 定理6.10]．
\begin{align} \sum_{\omega\in {\rm Dyck}(n)}q^{{\rm maj}(\omega)}= \frac{1}{[n+1]_q}\binom{2n}{n}_q \end{align}
本稿を通じて以下の$q$-類似を表す記号を使う．
\begin{align}
[n]_q&\triangleq 1+q+\cdots+q^{n-1},\\
[n]_q!&\triangleq [1]_q[2]_q\cdots[n]_q,\\
\binom{n+r}{r}_q&\triangleq
\frac{[n+r]_q!}{[n]_q![r]_q!}.
\end{align}
$q$-二項係数が満たす以下の性質は，もう知ってるとする．（計算すればわかる．）
この式については例えば [2]にも書いてある．
\begin{align} \binom{n+r}{r}_q=\binom{n+r}{n}_q \end{align}
\begin{align} \binom{n+r}{r}_q=q^{n}\binom{n+r-1}{r-1}_q+\binom{n+r-1}{r}_q \end{align}
準備
major index
全順序集合$S$の語 (注：語とは元の有限列のことだと思ってよい)$\omega=\omega_1\omega_2\cdots\omega_r\quad(\omega_i\in S)$に対して，その降下点集合 (set of descents) $D(\omega)$を
\begin{align}
D(\omega)\triangleq\{i\mid\omega_i>\omega_{i+1}\}
\end{align}
と定める．そして，語$\omega$のmajor index ${\rm maj}(\omega)$を，
\begin{align}
{\rm maj}(\omega)\triangleq\sum_{i\in D(\omega)}i
\end{align}
と定める．
$S\triangleq\{1,2,\ldots,8\}$で$\omega=47523816$なら，$D(\omega)=\{2,3,6\}$であり${\rm maj}(\omega)=2+3+6=11$である．
$S\triangleq\{A,B\}\ (A>B)$で$\omega=BABAABBAB$なら，$D(\omega)=\{2,5,8\}$であり${\rm maj}(\omega)=15$である．
正方格子路
次に，正方格子路を定義する．ベクトル$\mathsf{A,B}$を$\mathsf{A}\triangleq(1,0)$，$\mathsf{B}\triangleq(0,1)$と定める．
点$(0,0)$から$(n,r)$への正方格子路とは，
語$\omega=\omega_1\cdots\omega_{n+r}\qquad(\omega_i\in\{\mathsf{A,B}\})$
で，その総和が
$\omega_1+\cdots+\omega_{n+r}=(n,r)$を満たすものである．
$(0,0)$から$(n,r)$への正方格子路の集合を$L(n,r)$とかく．
ベクトル$\mathsf{A,B}$の順序関係を$\mathsf{A}>\mathsf{B}$と定めることにより，集合$L(n,r)$の上の関数${\rm maj}$を定義する．
正方格子路の反転操作
正方格子路の集合$L(n,r)$の部分集合で，末尾が$\mathsf{A},\mathsf{B}$であるものをそれぞれ
\begin{align}
L_\mathsf{A}(n,r)\triangleq\{\omega=\omega_1\cdots\omega_{n+r}\in L(n,r)\mid \omega_{n+r}=\mathsf{A}\},\\
L_\mathsf{B}(n,r)\triangleq\{\omega=\omega_1\cdots\omega_{n+r}\in L(n,r)\mid \omega_{n+r}=\mathsf{B}\}
\end{align}
と定める．
$\omega\in L(n,r)$に対する操作$\textrm{flip}$を，$\omega$に出てくる$\mathsf{A}$と$\mathsf{B}$を，をれぞれ$\mathsf{B}$と$\mathsf{A}$に入れ替える操作と定義する．
すると，$\textrm{flip}$は$L_\mathsf{A}(n,r)$から$L_\mathsf{B}(r,n)$への全単射であり，
$\omega\in L_\mathsf{A}(n,r)$に対して
\begin{align}
\textrm{maj}(\textrm{flip}(\omega))-r=
\textrm{maj}(\omega)
\end{align}
が成り立つ．
これを示すために，正方格子路を置換として扱う方法を考える．
正方格子路の置換への埋め込み
$(0,0)$から$(n,r)$への正方格子路を$n+r$文字の置換へ写す単射
$\sigma_\bullet\colon L(n,r)\to\mathfrak{S}_{n+r}$をつくる．
$\omega=\omega_1\cdots\omega_{n+r}\in L(n,r)$とする．
$\omega_i=\mathsf{B}$となるような添字$i$を，小さい順に$i_1,\ldots,i_r$とする．
また，$\omega_j=\mathsf{A}$となるような添字$j$を，小さい順に$j_1,\ldots,j_n$とする．
そして，置換$\sigma_\omega\in\mathfrak{S}_{n+r}$を
\begin{align}
\sigma_\omega(i_k)&\triangleq k,\qquad(k=1,\ldots,r)\\
\sigma_\omega(j_k)&\triangleq r+k,\qquad(k=1,\ldots,n)
\end{align}
と定める．
下記上段の$\omega\in L(6,4)$に対して，下記下段の$\sigma_\omega\in\mathfrak{S}_{10}$をえる．
\begin{align}
\begin{array}{ccccccccccc}
\omega=&
\mathsf{A}&
\mathsf{B}&
\mathsf{A}&
\mathsf{B}&
\mathsf{B}&
\mathsf{A}&
\mathsf{A}&
\mathsf{B}&
\mathsf{A}&
\mathsf{A},\\
\sigma_\omega=&
5&1&6&2&3&7&8&4&9&10.
\end{array}
\end{align}
左にある$\mathsf{B}$から順にラベル$1,2,,\ldots$をつけて，それが終わったら左にある$\mathsf{A}$から順にラベル$r+1,r+2,\ldots$をつけると思ってもよい．絵で描くと以下のような感じになる．
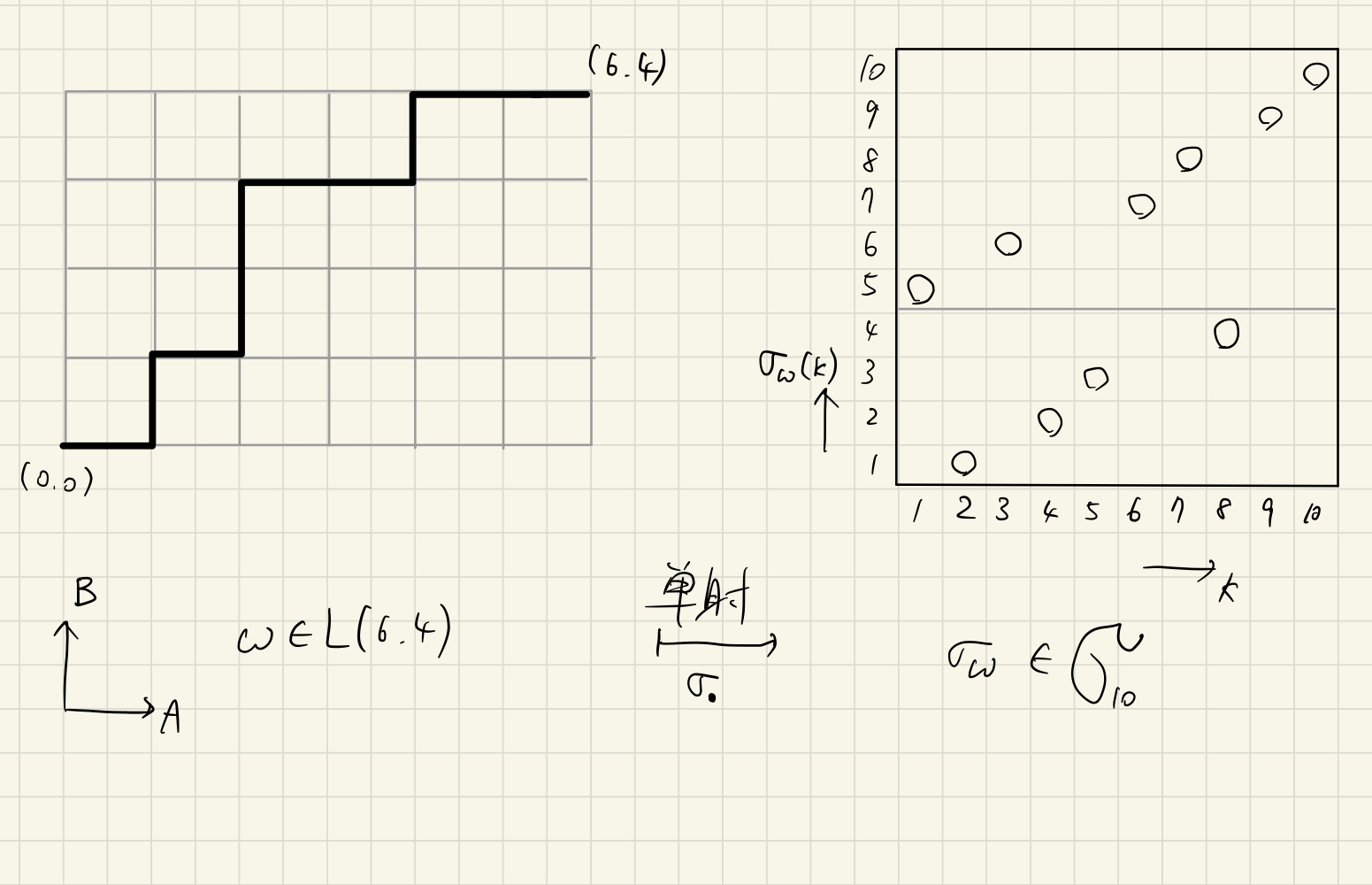埋め込みの例
この単射は，統計量$\textrm{maj}$を保存する．つまり，
$\omega\in L(n,r)$に対して$\textrm{maj}(\omega)=\textrm{maj}(\sigma_\omega)$.
次に，置換を，majが1大きい別の置換に写す操作を考える．
$\{1,\ldots,n\}$の置換$\sigma=\sigma_1\cdots\sigma_n\in\mathfrak{S}_n\ (\sigma_i\in\{1,\ldots,n\})$が$\sigma_n\neq 1$を満たすとし，$\sigma_i=1\ (i< n)$だとする．
置換$\varphi(\sigma)\in\mathfrak{S}_n$を
\begin{align}
\varphi(\sigma)\triangleq
(\sigma_1-1)\cdots(\sigma_{i-1}-1)n(\sigma_{i+1}-1)
\cdots(\sigma_{n}-1)
\end{align}
と定める．すると，
\begin{align}
{\rm maj}(\sigma)+1={\rm maj}(\varphi(\sigma))
\end{align}
が成立．
言葉で書くと，写像$\varphi$は，置換に出てくる$1$を$n$に変えて，それ以外を全部$-1$する写像である．
もし$i\neq 1$ならば，$i-1\in D(\sigma),i\notin D(\sigma)$であり，
\begin{align}
D(\varphi(\sigma))=(D(\sigma)\setminus \{i-1\})\cup \{i\}
\end{align}
が成り立つのでmajor indexが$1$増える．
もし$i=1$ならば，$1\notin D(\omega)$であり，
\begin{align}
D(\varphi(\sigma))=D(\sigma)\cup\{1\}
\end{align}
なので，この場合もmajor indexが$1$増える．
$\sigma=47523816$のとき$\varphi(\sigma)=36412785$.
$D(\sigma)=\{2,3,6\},\ D(\varphi(\sigma))=\{2,3,7\}$.
![補題5の写像!FORMULA[113][1017910466][0]の説明](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F1agHa789vsRBfYowgq5f.png?alt=media)
補題5の写像$\varphi$の説明
絵で描くと、写像$\varphi$は、一番下の段を一番上に移動することに相当する。
$\omega\in L_\mathsf{A}(n,r)$とし，置換への埋め込み$\sigma_\omega$を考える．
$\omega$の末尾が$\mathsf{A}なので，$この置換$\sigma_\omega$は，
\begin{align}
\varphi^k(\sigma_\omega)(n)\neq 1,\quad(k=0,\ldots,r-1)
\end{align}
を満たし，写像$\varphi$を$r$回当てることができる．
そして，$\varphi^r(\sigma_\omega)$は，$\textrm{flip}(\omega)$の埋め込みである．補題5より
\begin{align}
\textrm{maj}(\sigma_\omega)+r=\textrm{maj}(\varphi^r(\sigma_\omega))
\end{align}
であり，補題4から
\begin{align}
\textrm{maj}(\omega)+r=
\textrm{maj}(\textrm{flip}(\omega))
\end{align}
を得る．
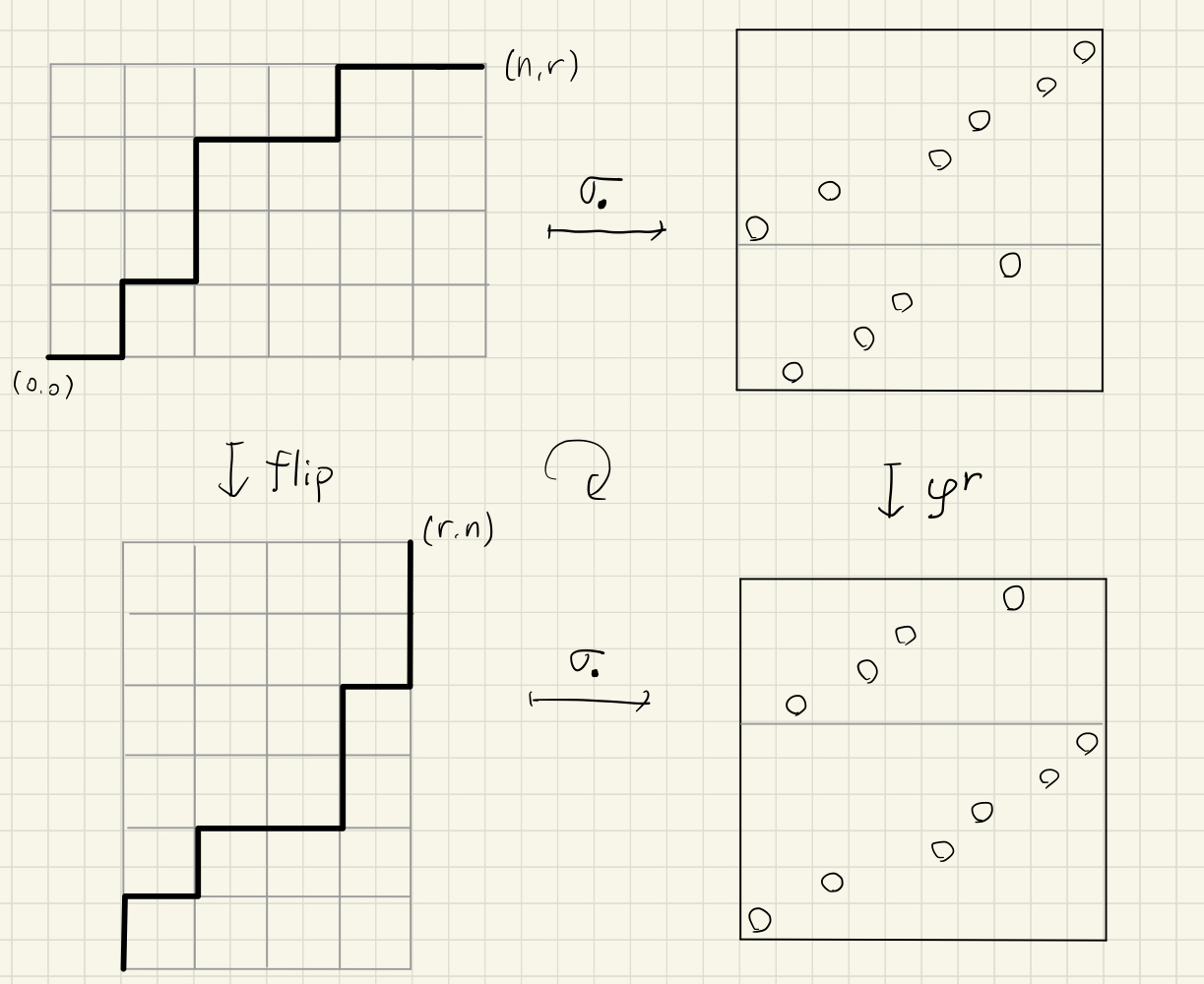補題3の説明
写像$\textrm{flip},\sigma_\bullet,\varphi$は上図のような可換図式で表される関係にある．
定理1の証明
母関数$\sum_{\omega\in L(n,r)}q^{{\rm maj}(\omega)}$が，以下の漸化式を満たすことを示す．
\begin{align} \sum_{\omega\in L(n,r)}q^{{\rm maj}(\omega)}= q^n\sum_{\omega\in L(r-1,n)}q^{{\rm maj}(\omega)}+ \sum_{\omega\in L(n-1,r)}q^{{\rm maj}(\omega)}. \end{align}
正方格子路$\omega=(\omega_1,\ldots,\omega_{n+r})\in L(n,r)$の最後のステップ$\omega_{n+r}$が$\mathsf{A,B}$のどちらなのか注目すると，以下のように書ける．
\begin{align} \sum_{\omega\in L(n,r)}q^{{\rm maj}(\omega)}= \sum_{\substack{\omega\in L(n,r),\\ \omega_{n+r}=\mathsf{B}}}q^{{\rm maj}(\omega)}+ \sum_{\substack{\omega\in L(n,r),\\ \omega_{n+r}=\mathsf{A}}}q^{{\rm maj}(\omega)}. \end{align}
最後のステップが$\mathsf{A}$なら，それを取り去ってもmajor indexは変化しないから，まず
\begin{align}
\sum_{\substack{\omega\in L(n,r),\\ \omega_{n+r}=\mathsf{A}}}q^{{\rm maj}(\omega)}=
\sum_{\omega\in L(n-1,r)}q^{{\rm maj}(\omega)}
\end{align}
が言える．
次に，最後のステップが$\mathsf{B}$なら，補題3で定義した操作flipを当てる．すると，flipしたあとの格子路は最後のステップが$\mathsf{A}$になるから，それを取り除く，つまり
\begin{align}
\sum_{\substack{\omega\in L(n,r),\\ \omega_{n+r}=\mathsf{B}}}q^{{\rm maj}(\omega)}
=
q^n\sum_{\substack{\omega\in L(r,n),\\ \omega_{n+r}=\mathsf{A}}}q^{{\rm maj}(\omega)}
=
q^n\sum_{\omega\in L(r-1,n)}q^{{\rm maj}(\omega)}.
\end{align}
$n+r$に関する帰納法による．命題6に帰納法の仮定を使い，二項係数の対称性 (公式1)，パスカルの三角形 (公式2)を使って式変形する．
\begin{align}
\sum_{\omega\in L(n,r)}q^{{\rm maj}(\omega)}
&=
\binom{n+r-1}{r}_q+q^n\binom{n+r-1}{n}_q\\
&=\binom{n+r-1}{r}_q+q^n\binom{n+r-1}{r-1}_q\\
&=\binom{n+r}{r}_q
\end{align}
