漸化式の話メモ

こんにちは、itouです。
注：以下の内容は数値計算で得られた結果をもとにしています。厳密な証明はしていません。

唐突な導入

$f,g,h$を多項式として、
$$f(n)a_{n+1}=g(n)a_n+h(n)a_{n-1}\tag{1.0}\label{name1}$$という漸化式を考えます。
この漸化式を満たす一般項のもつ性質について解説します。

直交性

\ref{name1}の解は直交性をもつことがあります。

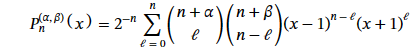ヤコビ多項式
この式をヤコビ多項式といい、次の漸化式を満たします。
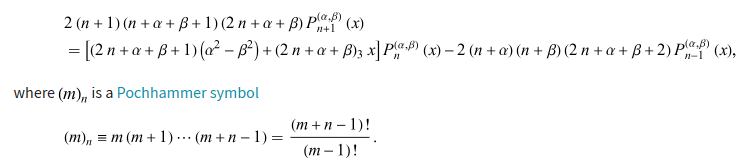漸化式
TEX打ちめんどくさかった
ヤコビ多項式は直交性をもつことが知られています。
ファヴァールの定理 というものがあり、\ref{name1}の解はパラメータｘを導入すると直交多項式になるそうです（私はあんまり理解してないですが）

リーマンゼータ関数との関係

$f(n)=(n+1)^r,h(n)=-cn^r$(cは定数)のとき、解はリーマンゼータ関数と密接なかかわりをもちます。
次のように同じ漸化式を２つ用意します。
$(n+1)^ra_{n+1}=g(n)a_n-cn^ra_{n-1}$
$(n+1)^ra'_{n+1}=g(n)a'_n-cn^ra'_{n-1}$
ただし、$a_n,a'_n$は初期条件が異なる、違う関数です。
それぞれに$a'_n,a_n$をかけて辺辺引くと、
$(n+1)^r(a_{n+1}a'_n-a'_{n+1}a_n)=cn^r(a_{n}a'_{n-1}-a'_{n}a_{n-1})$
$(n+1)^r(a_{n+1}a'_n-a'_{n+1}a_n)=c^n(a_{1}a'_{0}-a'_{1}a_{0})$より、
$ \sum_{n=0}^{\infty}(a_{n+1}a'_n-a'_{n+1}a_n)=\sum_{n=1}^{\infty}\frac{c^{n-1}(a_{1}a'_{0}-a'_{1}a_{0})}{n^r}$

$c=1$のとき、右辺はリーマンゼータ値そのものですね。
例えばアペリーの数列$a_n=\sum_{k=0}^{n}{ n \choose k }^2{ n+k \choose k }^2$は$(n+1)^3a_{n+1}=(34n^3+51n^2+27n+5)a_n-n^3a_{n-1}$を満たします。

私が見つけた例

上のように\ref{name1}は良い性質を持っていますし、 この記事 のように積分ともかかわりがあったりします。いろいろと面白い性質をもっているので、一般的に解きたいのですが、力不足で全然解法がわからないです……なので解になりそうな関数をもってきて、その漸化式を導く、という方法で漸化式と解のセットの例をつくりました。

1.$a_n=\sum_{k=0}^{n}{ n-2 \choose k }{ n \choose k }^2$は$ (n+1)^2(3n^2-n-6)a_{n+1}=n(n+1)(21n^2-7n-10)a_n+8n(n-2)(3n^2+5n-4)a_{n-1}$を満たす。

2.$a_n=\sum_{k=0}^{n}{ n-3 \choose k }{ n \choose k }^2$は$ (n+1)^2(2n^2-5n-2)a_{n+1}=(14n^4-21n^3-8n^2+5n+2)a_n+8n(n-2)(2n^2-n-5)a_{n-1}$を満たす。

3.$a_n=\sum_{k=0}^{n}{ 2k \choose k }^3$は$ (n+1)^3a_{n+1}=(65n^3+99n^2+51n+9)a_n-8(2n+1)^3a_{n-1}$を満たす。

4.$a_n=\sum_{k=0}^{n}{ 2k \choose k }^6$は$ (n+1)^6a_{n+1}=(17n^2+18n+5)(241n^4+468n^3+338n^2+108n+13)a_n-64(2n+1)^6a_{n-1}$を満たす。

5.$a_n=\sum_{k=0}^{n}{ n+k \choose k }^2$は$ 2(n+1)^2(2n+3)(21n+8)a_{n+1}=(1365n^4 +3943n^3 +3879n^2+ 1605n +240)a_n-4n(2n+1)^2(21n+29)a_{n-1}$を満たす。

6.$a_n=\sum_{k=0}^{n}{ 3k \choose k }{ 2k \choose k }^2$は$ (n+1)^3a_{n+1}=(109n^3+55n^2+27n+13)a_n-6(3n+1)(3n+2)(2n+1)a_{n-1}$を満たす。

7.$a_n=\sum_{k=0}^{n}{ 3k\choose k }^2$は$ 4(2n+1)^2(n+1)^2a_{n+1}=(745n^4+1506n^3+1105n^2+348n+40)a_n-9(3n+1)^2(3n+2)^2a_{n-1}$を満たす。

課題

１．リーマンゼータ関数と関係のある漸化式と解のセットを他に見つける
２．直交多項式となる解を、ヤコビ多項式以外に見つける
３.解の積分表示を一般に求める
今後はこれらの課題に取り組みます。

謝辞

読んで下さりありがとうございました。誤植指摘お願いいたします。