積分botの数式を漸化式で解く議論

はじめまして！まぐな氏という者です。(｀・∀・´)
まったり数学部屋(LINE OC)にて、面白い議論が出たので紹介します。

発端

ことの発端は、積分botの数式を数楽が解いた 記事 であった。

数楽はこれを超幾何級数を用いて解いている。
今回の議論は、これを漸化式で初等的に解けないか？というものである。

昼頃、 Sillpherth が面白い漸化式を弾き出した。
後に、本人が覚書を書いていたので一応 コチラ から読めます。
(しかし、到底読めたもんじゃねぇので、以下に解説する。)

まずは、これを証明して行く。
如何せんゴチャゴチャするので、何個かに分けて証明し、後に纏めるという形式にする。
証明を閉じておけばゴチャゴチャ感は減る、、はず。
$\bigstar$は流れのまとめの際に式の引用として用いる。

この後ろの積分について更に部分積分を行う。

これを用いて、
\begin{align*} \qquad \int_{0}^{\pi}&\frac{\sin^{2n}x \left((2n+1) \cos^2 x- \sin^{2}x\right)}{(1-2r\cos x+r^{2})^{n+1}} dx\\[3mm] &=(2n+1)\int_{0}^{\pi}\frac{\sin^{2n}x}{(1-2r\cos x+r^{2})^{n+1}} dx\\[2mm] &\qquad -2(n+1)\int_{0}^{\pi}\frac{\sin^{2n+2}x}{(1-2r\cos x+r^{2})^{n+1}} dx \end{align*}
前者は$I_{n}$に他ならない。
$$\qquad=(2n+1)I_{n}-2(n+1)\int_{0}^{\pi}\frac{\sin^{2n+2}x}{(1-2r\cos x+r^{2})^{n+1}} dx$$
考えるべきは最後の積分のみである。

残った積分は$\bigstar1$で出てきた形であることに気が付く！！
そう！！ついに同型が出てきたのである！！
ここで、$\bigstar1$を逆に用いて、
$$\int_{0}^{\pi}\frac{\sin^{2n+2}x\cos x}{(1-2r\cos x+r^{2})^{n+2}}dx=\frac{2r(n+2)}{2n+3}I_{n+2}$$
と分かる。以上の流れをまとめ、漸化式を作る。

長くゴチャゴチャした証明が漸く終わりを告げた。
これを見せつけてきたSillpherthは、私にこれを解けと言ってきた。
このくらい解いてやらぁ！

これを証明して行く。

$I_0$と$I_1$を求める(Sillpherth)

ここで、$I_{0}$と$I_{1}$がまだ分かっていないので、これを求める。

$I_0$は簡単に示せるので、まずは$I_0$を計算する。

これを用いて、$I_1$も求められる。
\begin{align*} I_{1} =& \frac{1}{4r^2}\left((1+r^2)\frac{\pi}{|1-r^2|} - \pi\right)\\ =& \frac{\pi}{4r^2}\left(\frac{1+r^2}{|1-r^2|} - 1\right) \end{align*}
後のことを考えて、これを場合分けしておく。

$|r|<1$のとき(MAGNA)

つまり$|r|<1$のとき、定理2の右辺が0になるということである。
$$\qquad I_{n+1}-\frac{2n+1}{2(n+1)}I_{n}=0$$
つまり、
$$\qquad I_{n+1}=\frac{2n+1}{2(n+1)}I_{n}$$
これは簡単に解くことができて、
\begin{align*} \qquad I_{n}&=\frac{(2n-1)!!}{(2n)!!}I_{0}\\[2mm] &=\frac{(2n)!}{2^{2n}n!^2}\frac{\pi}{1-r^2}\\ &=\frac{\pi}{2^{2n}(1-r^2)}\binom{2n}{n} \end{align*}

$|r|>1$のとき。(砂消しゴムさん)

もうとっくに忘れたであろう定理2を引用して、
$$\qquad I_{n+1}-\frac{2n+1}{2(n+1)}I_{n}=\frac{1}{(2r)^{2n}}\frac{(2n+1)!}{n!(n+1)!}\left(I_{1}-\frac{I_{0}}{2}\right)$$
この$\displaystyle I_{1}-\frac{I_{0}}{2}$に上の値を入れると、
$$\qquad I_{n+1}-\frac{2n+1}{2(n+1)}I_{n} =-\frac{2\pi}{(2r)^{2n+2}}\frac{(2n+1)!}{n!(n+1)!}$$
これを具体的に書き出して、発見法的に解は得られていた。(深夜2:30)
しかし、具体的にどのように漸化式を解けば良いのか分からなかった。

この漸化式の解き方は砂消しゴムさんに教えていただいた。
　　　　砂消しゴムさんのツイート
砂消しゴムさんに教えていただいた数式

解説のギャップが(私にとって)やや大きく、$I'_{n}$の一般項の部分を中々埋めれず困っていたらゴスロリ有給休暇さんが解説して下さった。
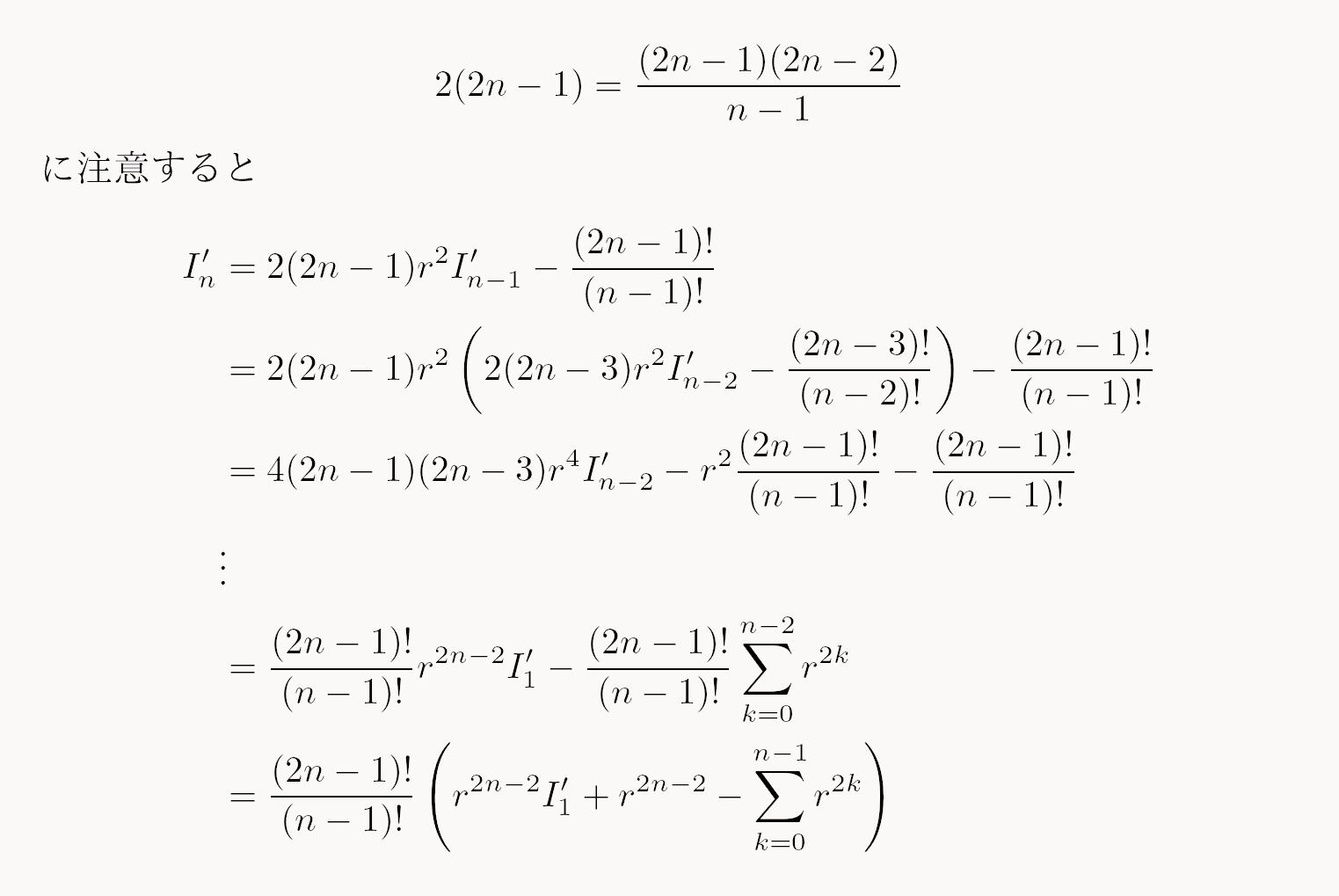ゴスロリ有給休暇さんに書いていただいた解説
確かに書き出してみると分かりやすいですね。
私は$I_1$から一般化しようとして事故ってたので今後の参考にしたい。

ついでに$I'_n$から$I_n$を出すところも埋めておく。
$I'_n$から$I_n$を出すとこ
ここで、$\displaystyle I_1=-\frac{\pi}{2r^2}\frac{1}{1-r^2}$であるから、括弧の中を整理すると、
\begin{align*} \qquad 4&I_1+\frac{2\pi}{r^2}-\frac{2\pi(r^{2n}-1)}{r^{2n}(r^2-1)}\\ &=-\frac{2\pi}{r^2}\frac{1}{1-r^2}+\frac{2\pi}{r^2}-\frac{2\pi(r^{2n}-1)}{r^{2n}(r^2-1)}\\ &=-\frac{2\pi}{1-r^2}\left(\frac{1}{r^2}-\frac{1-r^2}{r^2}-\frac{r^{2n}-1}{r^{2n}}\right)\\ &=-\frac{2\pi}{1-r^2}\left(\frac{1}{r^2}-\frac{1}{r^2}+1-1+\frac{1}{r^{2n}}\right)\\ &=\frac{2\pi}{r^{2n}(r^2-1)} \end{align*}
よって、
\begin{align*} I_{n}&=\frac{1}{4^n}\binom{2n-1}{n}\left(4I_1+\frac{2\pi}{r^2}-\frac{2\pi (r^{2n}-1)}{r^{2n}(r^2-1)}\right)\\[2mm] &=\frac{1}{4^n}\frac{(2n-1)!}{n!(n-1)!}\frac{2\pi}{r^{2n}(r^2-1)}\\ &=\frac{\pi}{(2r)^{2n}}\frac{1}{r^2-1}\binom{2n}{n} \end{align*}
よって、$|r|<1,|r|>1$の両方のパターンについて、漸化式で積分Botの式を示すことができた。
$$\qquad \int_{0}^{\pi}\frac{\sin{x}^{2n}}{(1-2r\cos{x}+r^{2})^{n+1}}dx= \begin{eqnarray} \left\{ \begin{array}{l} \displaystyle \frac{\pi}{2^{2n}}\frac{1}{1-r^2}\binom{2n}{n} \quad \, \cdots |r|<1\\ \displaystyle \frac{\pi}{(2r)^{2n}}\frac{1}{r^2-1}\binom{2n}{n} \cdots |r|>1 \end{array} \right. \end{eqnarray} $$

あとがき

最初にSillpherthにもって来られた画像の酷さを紹介しておこう。

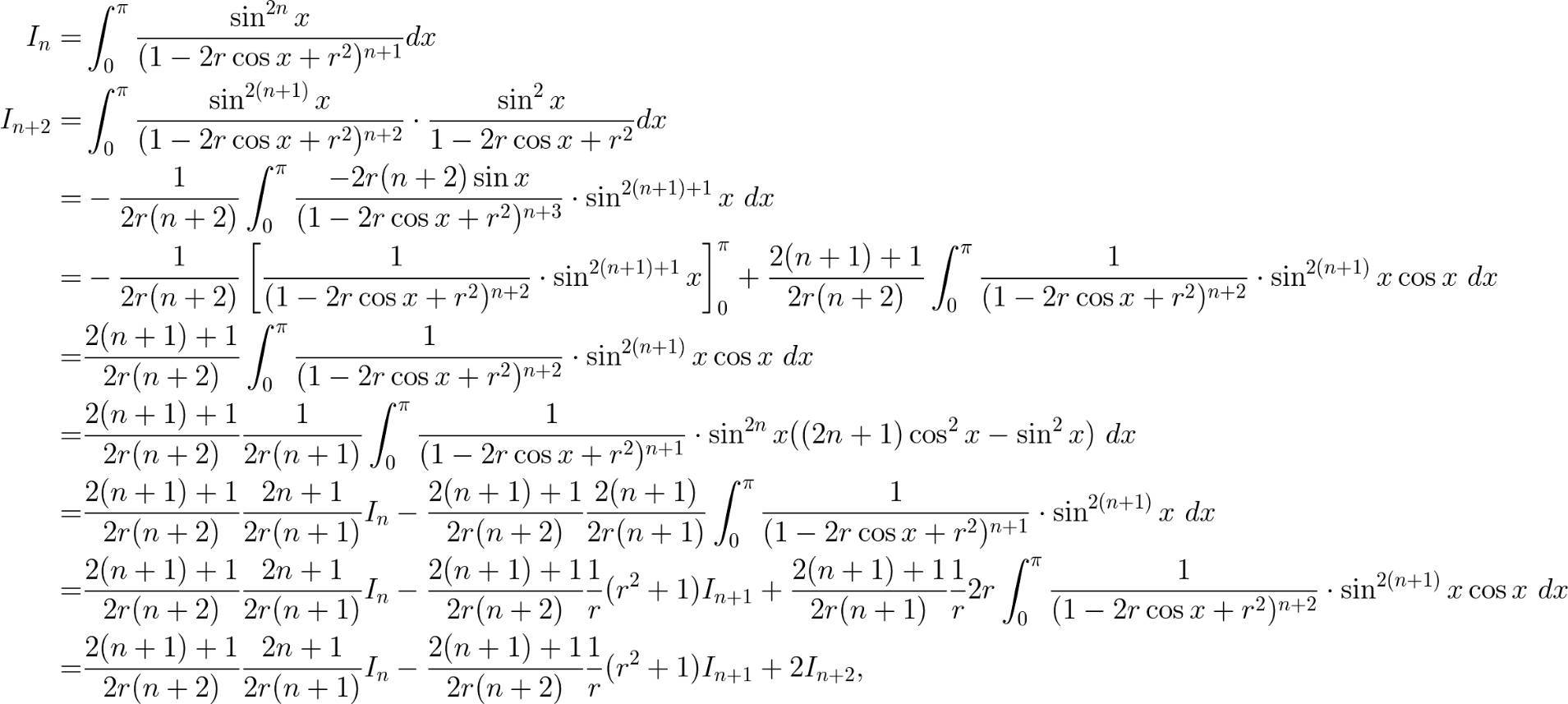ゴミ
これはかなり解読に苦労しました、。

$|r|>1$の場合の漸化式の解き方を考えて、深夜の2:30まで粘って、諦めて寝たら、朝起きたらゴスロリ有給休暇さんに3行で解かれてて笑いました。
思いつかんかった、、

この記事の編集がようやっと終わったころ、「これで良くないですか？」と、ゴスロリ有給休暇さんに漸化式で解かれてしまった。
つよすぎんよ、
若干、哀愁が漂い始めたところで、今回は終わりにしたいと思います。
ここまで読んでくださり、ありがとうございました。

気が向けば、またいつか記事を書きます。ほなまた。(*´∀`)ﾉｼ