コラッツ操作の式の変形版における考察→1に到達するのは2種類！？【3x+1】と【x+1】

コラッツ予想の計算において、奇数の場合に施す計算「3x+1」がいろいろな形に変形され、変形すると予想は成立しないというような記述を見かけたことがあります。
実際「3x+1」以外の計算でやってみると、ループして、1にたどりつかない数が出てきた経験がわたしにもあります。

コラッツ予想では奇数のときの計算は「3x+1」であるわけですから、変形した式でループするからと言って、「3x+1」でもループするとは言えないわけですが、とっかかりを見つけられるかもしれませんから、いろいろな式で計算してみたくなりますね！

そうやって、考察した結果、「x+1」では、「3x+1」同様に1に到達するのではとわたしは考えています。

推測なのですが、1に到達する奇数の式は、「3x+1」と「x+1」の2つのみなのではないかと考えています。なぜそう考えたのか、それは、「3x+1」の本来のコラッツ予想を証明する過程で、「3x+1」と「x+1」の一般項で示せる数列が対になっていることに気づいたためです。

「x+1」のときは、偶数のならびの一般項は、「3x+1」のときと同じです。
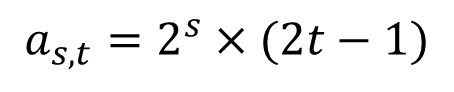偶数の一般項

奇数のならびの一般項は、次のような式になります。
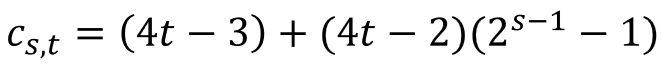「x+1」における奇数の一般項

（この式は、「3x+1」のときと同様に計算結果の数列の漸化関係から推測した一般項ですが、cの式を展開して計算した結果は、偶数aの式からマイナス1した式になります！）

cの式のsに1,2,3,4…と代入して、sを定数としたときの式を求めると、「3x+1」のときの式と対になっていることがわかります（左列がs=1,2,3…を代入したc_s,tの式、右列がs=1,2,3…を代入したb_s,tの式）。
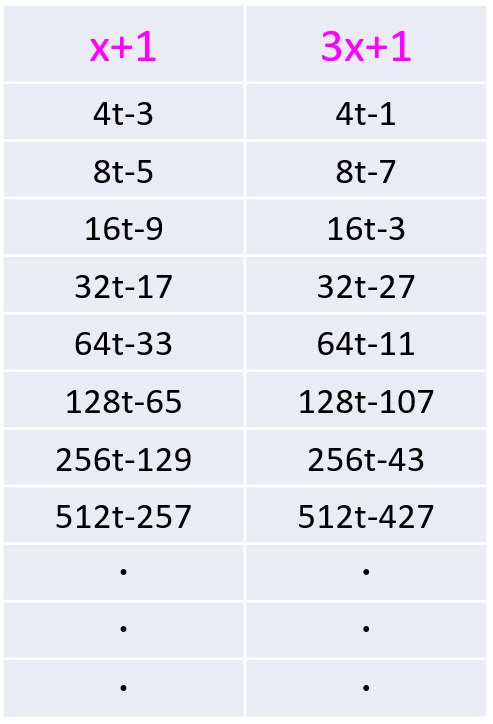tの式の比較

「x+1」で計算したときに、いつでも1に到達するのは必然な感じを受け、「3x+1」のときほど不思議な感じを受けないのですけれど、数の並びを表す式が対になっていることはとても興味深いことです。
このことが「3x+1」のときに示した奇数の一般項がコラッツ操作において成立していることを明確にしていると思いました。

コラッツ予想における奇数の一般項b_s,t「3x+1」については こちら の記事で述べています。