『柏陽祭2025問題G』の解説

はじめに

私が競技数学界隈に迷惑をかけ、Twitter、OMCから退いて月日が経ちました。未だに申し訳なく感じているのと、自分がこの記事を投稿することに対し不満に感じる方がいたらすみません。しかし、pororoccaで私がWriterを行ったコンテスト『柏陽祭2025』の解説が途中だったため、解説を楽しみにしている方がいることを期待して記事を書きます. ここでは問題Gを解説します。
他の問題の記事
『柏陽祭2025』の解説

コンテストサイト

以下のリンクから飛ぶことができます.
柏陽祭2025

問題文

正三角形$ABC, DEF$について, 三点$A, F, E$がこの順に同一直線上に並んでいます. また, 線分$AD$と線分$BE$の交点が存在したのでこれを$X$とすると三点$F, C, X$はこの順に同一直線上に並びました. 直線$BC$と直線$AE$の交点を$Y$としたとき, 以下が成立しました.
$$\angle CAE=\angle BEA,　AD=AY,　DX=1$$
このとき, 線分$AD$の長さの値の最小多項式を$f$とします. $f(5)$の値を求めてください.

$m$を根にもつ有理数係数多項式のうち, 次数が最小であり, かつ最高次の係数が$1$であるものを(このようなものは一意に存在します), $m$の最小多項式とよびます.

解説

図は以下のようになります. (一意に定まります.)

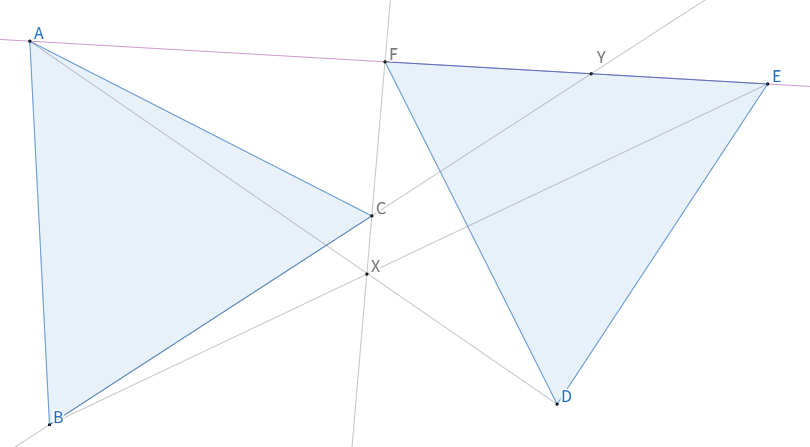
　三角形$ABC$と三角形$DEF$がこの順に対応していると考えます。三線$AD,BE,CF$が点$X$で交わっているため、$AB\cap DE=Z,CA\cap FD=W$とするとデザルグの定理より三点$YZW$は共線です。
三点$YZR$を加えた図
$\angle{CAB}=\angle{FDE}=60\degree$より四点$AZDW$は共円.　$\angle{ABC}=\angle{DEF}=60\degree$より四点$BYEZ$は共円.
よって$\angle{FDX}=\angle{WZA}=\angle{FEX}$より四点$DEFX$は共円.　$\angle{CAX}=\angle{WZD}=\angle{YBE}$より四点$ABXC$は共円.
$\angle{CAE}=\angle{BEA}=\angle{FDA},\angle{ACY}=\angle{DFA},AY=DA$より$\triangle{ACY}\equiv\triangle{DFA}. CA=FD$より$\triangle{ABC}\equiv\triangle{DEF}.$
$AD=x$とすると, $AX=x-1$.
$\angle{FED}=60\degree=\angle{EFD}=\angle{EXD}$より$\triangle{DEX}\backsim\triangle{DAE}$が成立するので${DX}\cdot{DA}=DE^2,DE=\sqrt{x}.$
$\angle{BZE}=\angle{AYC}=\angle{DAF}=\angle{BEZ}$より$BZ=BE.$メネラウスの定理より
$$\frac{{AB}\cdot{ZE}\cdot{DX}}{{BZ}\cdot{ED}\cdot{XA}}=\frac{{ZE}}{{BZ}\cdot(x-1)}=1$$
$BZ\cdot(x-1)=ZE$
$\cos{\angle{BEZ}}=\Large\frac{x-1}{2}$ (...①)
また, 円$DEF$について正弦定理より
$\Large\frac{\sqrt{x}}{\sin60\degree}=\frac{DX}{\sin\angle{XED}}$
$\sin\angle{BEZ}=\Large\frac{\sqrt{3}}{2\sqrt{x}}$ (...②)
①と②から、
$x^3-2x^2-3x+3=0$が得られるので,解答するべき値は$63$です。

感想

デザルグの定理を使う問題は珍しく、OMCでもあまり見かけないと思います。(と言いつつ私がOMCをやめて数か月後に開催された$OMCG002$で出題されたみたいですが...)デザルグの定理が見えてもその後のメネラウスの定理で上手く立式することができなかった方もいるかもしれません。メネラウスが非常に綺麗に刺さる問題で当コンテストD問題と並ぶ良問のように感じました。

最後に

　この問題はデザルグの定理が初手で見えないとやや厳しいかもしれません。知らなかった方はこの機会に触れておくと後々役に立つと思います。角度追跡のみで合同や二等辺三角形が分かるので比較的取り組みやすい問題です。個人的にはTester様が開催している『匿式図形問題エスパー杯』が連想されました。私は一度だけ出場したことがあるのですが、構図が綺麗な良問が多く未だに印象に残っている問題が数問あります。この記事を読んだ方々は是非そちらにも挑戦してみることをお勧めします。
　再度申し上げますが私の関係者の皆様、大変ご迷惑をお掛けしたことを深くお詫び申し上げます。