『柏陽祭2025』の解説

はじめに

こんにちは、ウラムの螺旋です. 先日pororocca上で開催されたコンテスト, 『柏陽祭2025』の単独Writerをしていました. 人生初のWriter リンクにしたい文字 だったので不備の有無に対する緊張と不安がありましたが, 沢山のTesterの協力のもと無事にコンテストを終えることができました. Testerの方々とコンテスト参加者には感謝しかないです. 今回は問題の解答と解説を書いていきます.

コンテストサイト

以下のリンクから飛ぶことができます.
柏陽祭2025

解答, 解説

問題A

問題文

正方形$ABCD$について, 直線$BC$上に点$E$を点$B, C$と重ならないようにとり, 正方形$AEFG$を正方形$ABCD$と向きが同じになるようにとります. 線分$CF$の長さが$8$のとき, 正方形$ABCD$と正方形$AEFG$の面積の差として考えられる値の総和を求めてください.

解説

点$E$の取り方は三点$B,C,E$の順番によって三通りに分けることができます。
　三点が$E,C,B$の順に並ぶ場合(図1)
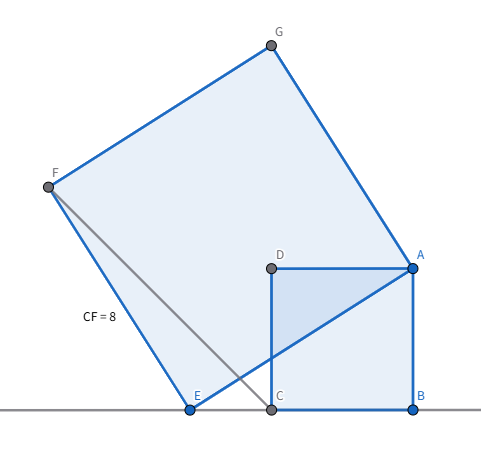
　三点が$C,E,B$の順に並ぶ場合(図2)
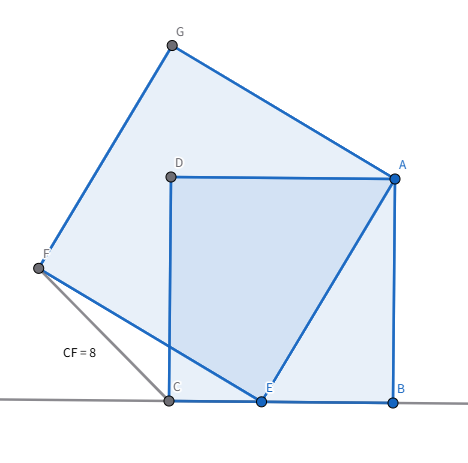
　三点が$C,B,E$の順に並ぶ場合(図3)
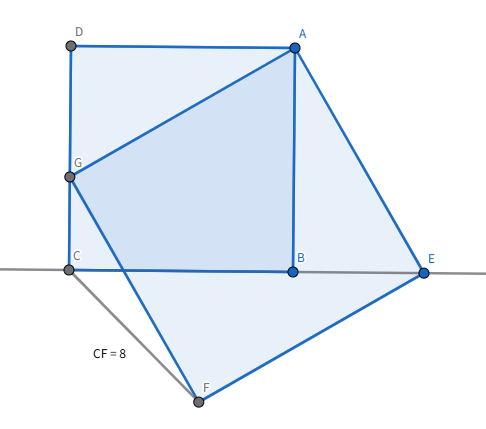
いずれの図でも, $AB=AD$, $AE=AG$, $\angle BAE=\angle DAG$が成立するので$\triangle BAE \equiv \triangle DAG$を示すことができ, $\angle ADG=\angle ABE=90°$が成立するため三点$C,D,G$は共線です. また, 四点$C,E,F,G$は共円で$EF=GF$, $\measuredangle CEF=\measuredangle CGF$, $\measuredangle FCG=\measuredangle FEG=45°$が成立しており, $△CEF$を線分$FE$が線分$FG$に重なるように回転移動させることができます.

• 図1の場合, 先ほどの合同より二つの正方形の面積の差は四角形$CEFG$の面積と等しいことが分かります. 回転移動から四角形の面積は等長な辺の長さが$8$の直角二等辺三角形の面積と同値です.
• 図2, 図3の場合, 先ほどの合同より二つの正方形の面積の差は$\triangle CEF$と$\triangle CGF$の面積の差と等しいことが分かります. 回転移動から等長な辺の長さが$8$の直角二等辺三角形を作ることができ, これが求めるべき面積と等しいです.

従って面積は$32$の一通りのみであり, これが提出すべき値です.

別解

点$F$から直線$BC$に下した垂線の足を$H$とすると$\triangle ABE \equiv \triangle EHF$がいずれの図でも成立し, $\measuredangle ECF=45°$まで分かれば$FH=4\sqrt{2}$が分かります. 二つの正方形の面積の差は$\triangle EHF$で三平方の定理を使うと$FH^2$と同値であることが分かり, これは$32$です.

問題B

問題文

辺$AB$と辺$BC$と辺$CD$の長さが等しい凸四角形$ABCD$について, 辺$BC$と辺$AD$の中点をそれぞれ$M$, $N$としたところ, 以下が成り立ちました.

$$ \angle BAD=75°,　\angle CDA=45°,　MN=3 $$

このとき, 四角形$ABCD$の面積は正整数$a, b$を用いて$a+\sqrt{b}$ と表すことができるので, $a+b$ の値を求めてください.

解説

直線$AB$と直線$CD$の交点を$E$, 直線$AC$と直線$BD$の交点を$F$とします. このとき$\angle BEC=60°, \angle CBE=2\angle BCA, \angle BCE=2\angle CBD$が成立するため$\angle CFD=\angle BCF+\angle CBF=60°=\angle BEC$より四点$BECF$は共円であり, $\angle BAC=\angle BCA=\angle BEF, \angle CDB=\angle CBD=\angle CEF$より点$F$が$\triangle ADE$の外心であり, $\angle FAD=\angle FDA=30°$も分かります.
線分$BD$の中点を$L$とすると中線連結定理と角度追跡から$ML=NL, \angle MLN=120°$が成立し, $MN=3$なので$NL=\sqrt{3}, AB=BC=CD=2\sqrt{3}$です.
$\angle BCE=30°, \angle CBE=90°$なので$BE=2, EC=4$であり, 四角形$ABCD$の面積は
$$ \frac{1}{2}(2+2\sqrt{3})(4+2\sqrt{3})\sin60°-2・2\sqrt{3}・\frac{1}{2}=9+3\sqrt{3} $$
特に解答するべき値は$36$です.

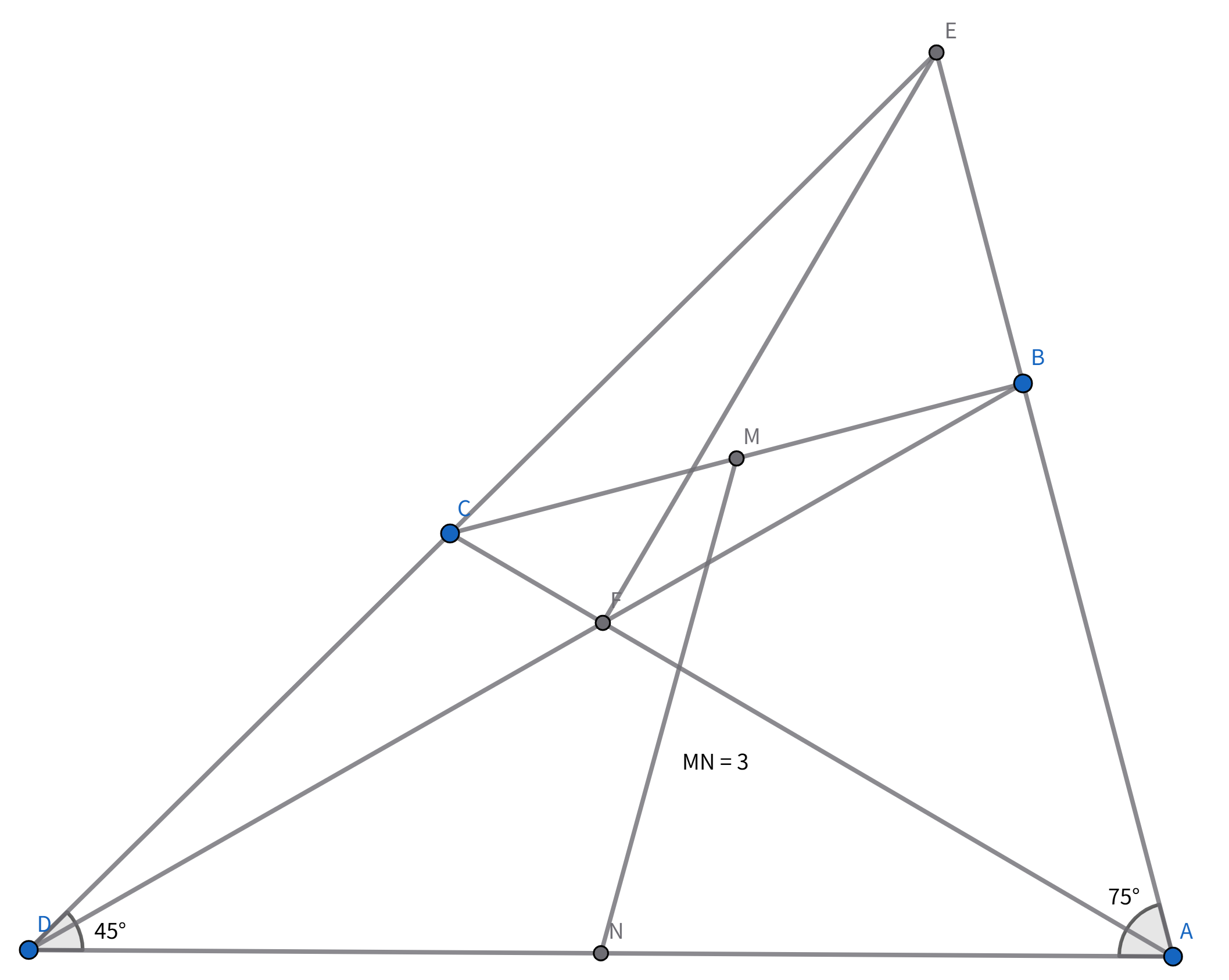
別解

四角形$ABMN$を線分$MB$が線分$MC$に重なるように回転移動させると平行四辺形を作ることができ, 点$A$の移動先を$A'$とすると$\triangle A'CD$は$\angle A'CD=120°$の二等辺三角形であり, $A'D=6$なので$CD=2\sqrt{3}$が求まります.
追記:『初等幾何bot構図集』でこの構図は紹介されており, $\angle ADB=\angle DAC=30\degree$をすぐに求めることができます.

問題C

問題文

鋭角三角形$ABC$について, 外接円を$Ω$, 垂心を$H$, 辺$BC$の中点を$M$, 点$H$から直線$AM$に下ろした垂線の足を$K$とします. 直線$BH, CH$と$Ω$の交点をそれぞれ$E(\neq B), F(\neq C)$とし, 線分$EF$の中点を$N$とします. さらに, 辺$AC$上(端点を除く)に点$P$をとると以下が成立しました.
$$ \triangle FNP \backsim \triangle AMC,　\angle PFA=\angle BAM,　BK=5 $$
このとき, 線分$PE$の長さの二乗としてありうる値の総和を求めてください.

解説

円$\Omega$の中心を$O$とすると, $\triangle OEF$は二等辺三角形なので点$N$は直線$AO$上にあります. また, 点$O$に関する点$A$の鏡映を$A'$, 点$M$に関する点$K$の鏡映を$K'$とすると垂心構図から$HM=A'M$であるため$\angle MK'A'=90°$であり, 点$K'$は円$\Omega$上にあります. また$\angle BAH=\angle BCH=\angle BAF, AB \perp HF$より$\triangle AHF$は二等辺三角形です. (点$E$も同様) 従って点$A$は円$HEF$の外心であり, $\angle BOC=2\angle BAC=\angle EAF$より$\triangle OBC \sim \triangle OEF$も分かります. 点$F$と点$P$は直線$AN$に関してそれぞれ点$B$側,点$C$側に位置しているため$\angle FNP>90°$が成立し, $\triangle FNP \backsim \triangle AMC$より$AC>AB$が分かります.
点$A$に関する点$H$の鏡映を$H'$とすると$\angle BAC=\angle EH'F,\angle ACB=\angle OCB+\angle OCA=\angle OCB+\angle HCB=\angle OCB+\angle HAB=\angle AFE+\angle AH'F=\angle AFE+\angle AFH'=\angle H'FE$
より$\triangle ABC \sim \triangle H'EF$が成立します. $\triangle ABC \sim \triangle H'EF, \triangle FNP \backsim \triangle AMC$から$\triangle EFP\sim\triangle CBK'$は自明です.
さらに本問では点$P$が線分$FN$よりも点$A$側にあるか点$C$側にあるかの二通りに分けることができ, それぞれ考察が必要になります.

• 点$P$が線分$FN$よりも点$C$側にある場合
  $\angle HAP=\angle EAP=2\angle EFP=2\angle CAM$より$\angle CAM=\angle HAM.$ $\angle PFA=\angle BAM$より$\triangle NAF$で角度を考えると$\angle BAM=45°$.また, $\angle AFN=\angle BAH$も分かり, $\angle ACF=\angle BCF$となるので$AC=BC.$ 直線$AM$と直線$CH$の交点が$\triangle ABC$の重心であることを踏まえると, $\tan\angle ABH=\tan\angle ACH=\frac{1}{3} $なので$EF:CB=HF:HB=2:\sqrt{10}.$ $CK'=BK=5$なので$PE=\sqrt{10}$です.
• 点$P$が線分$FN$よりも点$A$側にある場合
  $\angle PFN=\angle CAM=\angle NAM+\angle NAC=\angle NAM+\angle FAB, \angle PFA=\angle BAM$より$\angle BFC=\angle BAC=\angle FAN=45°.$ よって$EF:CB=HF:HB=\sqrt{2}:1$が成立し, $CK'=BK=5$なので$PE=5\sqrt{2}$です.
  従って解答するべき値は$60$です.

補足

「点$P$が線分$FN$よりも点$C$側にある場合」では$\triangle CEF$の内心が点$P$であること, 「点$P$が線分$FN$よりも点$A$側にある場合」では$AB//OK$が証明できます. また, 気づいた方がいるかもしれませんが点$N$が線分$EF$の中点, 点$A'$が円$HEF$の$E,F$接線の交点であるため, $\triangle H'EF$の点$H'$類似中線を考えると前者の場合では点$P$が線分$H'N$上に, 後者の場合では点$P$が線分$H'A'$上に位置します. 面白いですね.

問題D

問題文

$AB>AC$を満たす鋭角三角形$ABC$の外心を$O$, $\angle BAC$の二等分線と直線$BO$の交点を$D$とします.
円$ABC$について弧$BAC$の中点を$M$とし, 直線$AB$と直線$CM$の交点を$E$とすると以下が成り立ちました.
$$ \angle ADE=\angle AME,　AE=25,　BE=96 $$
このとき, 辺$AC$の長さは互いに素な正整数$a,b$を用いて$\Large\frac{a}{b}$と表せるので$a+b$の値を解答してください.

解説

こちらから飛ぶことができます.
柏陽祭2025問題Dの解説

問題E

問題文

半径が$14$の円$Ω$に内接し, $AB>AC$を満たす鋭角三角形$ABC$について, 内心を$I$, $A$傍心を$J$とする. 辺$AJ$の垂直二等分線と$Ω$の交点の内, 点$C$側にあるものを$D$, $B$側にあるものを$E$とし, 三角形$JBC$の外接円と三角形$JDE$の外接円の交点を$X(\neq J)$としたところ, 以下が成り立った.
$$ CX:CD=8:3,　AI=10 $$
辺$BC$と辺$DE$の交点を$F$としたときの線分$XF$の長さの二乗を求めてください.

解説

別の記事として投稿するのでそのリンクを貼る予定です.

問題F

問題文

$AB>AC$を満たす鋭角三角形$ABC$の外接円を$Ω$, 辺$BC$の中点を$M$とします. 点$B,C$から対辺に下した垂線の足をそれぞれ$E, F$とし, 直線$EF$と$Ω$の交点を$P, Q$とします. ただし, 四点$P, E, F, Q$はこの順に並ぶものとします. 円$MEF$と直線$MQ$の交点を$L(\neq M)$としたところ直線$AL$と直線$PM$が$Ω$上で交わりました.
$$ QL=PM=20 $$
が成立するとき, 線分$AP$の長さを二乗した値を求めてください.

解説

別の記事として投稿するのでそのリンクを貼る予定です.

問題G

問題文

正三角形$ABC, DEF$について, 三点$A, F, E$がこの順に同一直線上に並んでいます. また, 線分$AD$と線分$BE$の交点が存在したのでこれを$X$とすると三点$F, C, X$はこの順に同一直線上に並びました. 直線$BC$と直線$AE$の交点を$Y$としたとき, 以下が成立しました.
$$ \angle CAE=\angle BEA,　AD=AY,　DX=1 $$
このとき, 線分$AD$の長さの値の最小多項式を$f$とします. $f(5)$の値を求めてください.

$m$を根にもつ有理数係数多項式のうち, 次数が最小であり, かつ最高次の係数が$1$であるものを(このようなものは一意に存在します), $m$の最小多項式とよびます.

解説

別の記事として投稿するのでそのリンクを貼る予定です.

問題H

問題文

外接円を$\Omega$, 内心を$I$とする鋭角三角形$ABC$について, 円$Γ$は円$\Omega$に内接し, 辺$AC$, 辺$BC$にも接しています. 円$\Gamma$と円$\Omega$, 辺$AC$との接点をそれぞれ$T, D$とし, 直線$TD$と円$\Omega$の交点を$M(\neq T)$, 直線$AI$との交点を$F$, 直線$TI$と直線$AB$, 円$MDI$の交点をそれぞれ$G$, $K(\neq I)$とします. さらに, 円$MDI$内に点$H$をとったところ, これは円$TAK$上にありました. また, 円$GHK$と直線$MK$の交点を$J(\neq K)$とすると, 直線$GJ$, 直線$AK$, 円$TAD$が一点で交わったのでこれを$L$とします.
$$ FG=FH,　MJ:KJ=1:3,　LJ=30 $$
が成立するとき, 線分$IK$の長さを二乗した値を求めてください.

解説

別の記事として投稿するのでそのリンクを貼る予定です.

最後に

今回のコンテストは約4ヶ月かかったものだったので沢山の幾何愛好家に参加して貰えて良かったです. 自分も順位表を見て楽しむことができましたし, 解いた人から好評や感想なども貰えて, 嬉しかったです.
来年も「柏陽祭2026」を開催するかもしれないのでその時がもし来たら是非参加してください. (自分が受験生なので厳しいかもしれませんが...)
読んで頂きありがとうございました.