『柏陽祭2025問題D』の解説

はじめに

この記事は先日pororoccaで私がWriterを行ったコンテスト『柏陽祭2025』の問題Dの解説を主に書いています. 想定解が凄いので是非見てください. また, 他の解法も出てきたのでそれらも紹介しようと思います.
他の問題の記事
『柏陽祭2025』の解説

コンテストサイト

以下のリンクから飛ぶことができます.
柏陽祭2025

問題文

$AB>AC$を満たす鋭角三角形$ABC$の外心を$O$, $\angle BAC$の二等分線と直線$BO$の交点を$D$とします.
円$ABC$について弧$BAC$の中点を$M$とし, 直線$AB$と直線$CM$の交点を$E$とすると以下が成り立ちました.
$$ \angle ADE=\angle AME,　AE=25,　BE=96 $$
このとき, 辺$AC$の長さは互いに素な正整数$a,b$を用いて$\Large\frac{a}{b}$と表せるので$a+b$の値を解答してください.

解法1

図は以下のようになります.

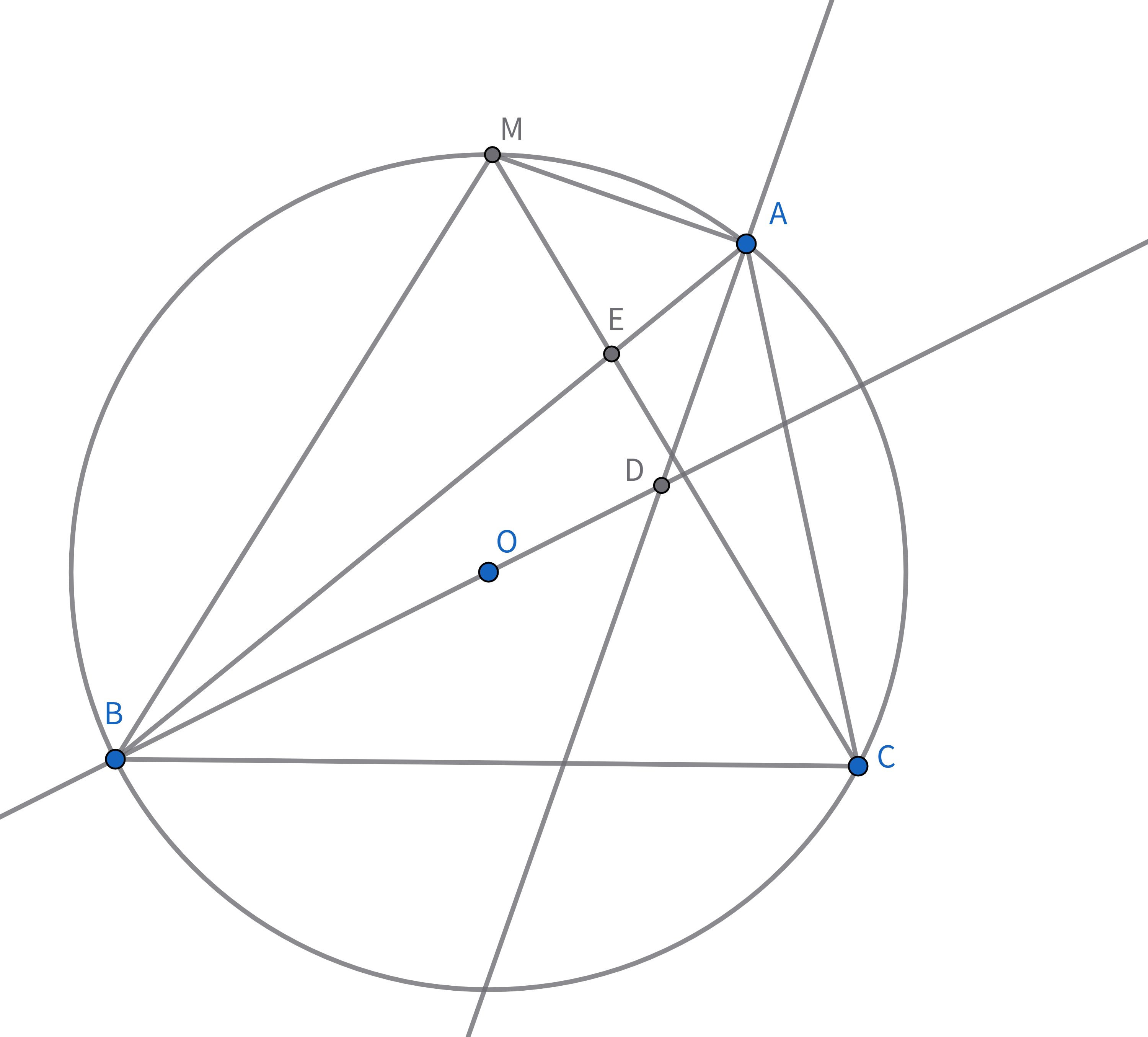
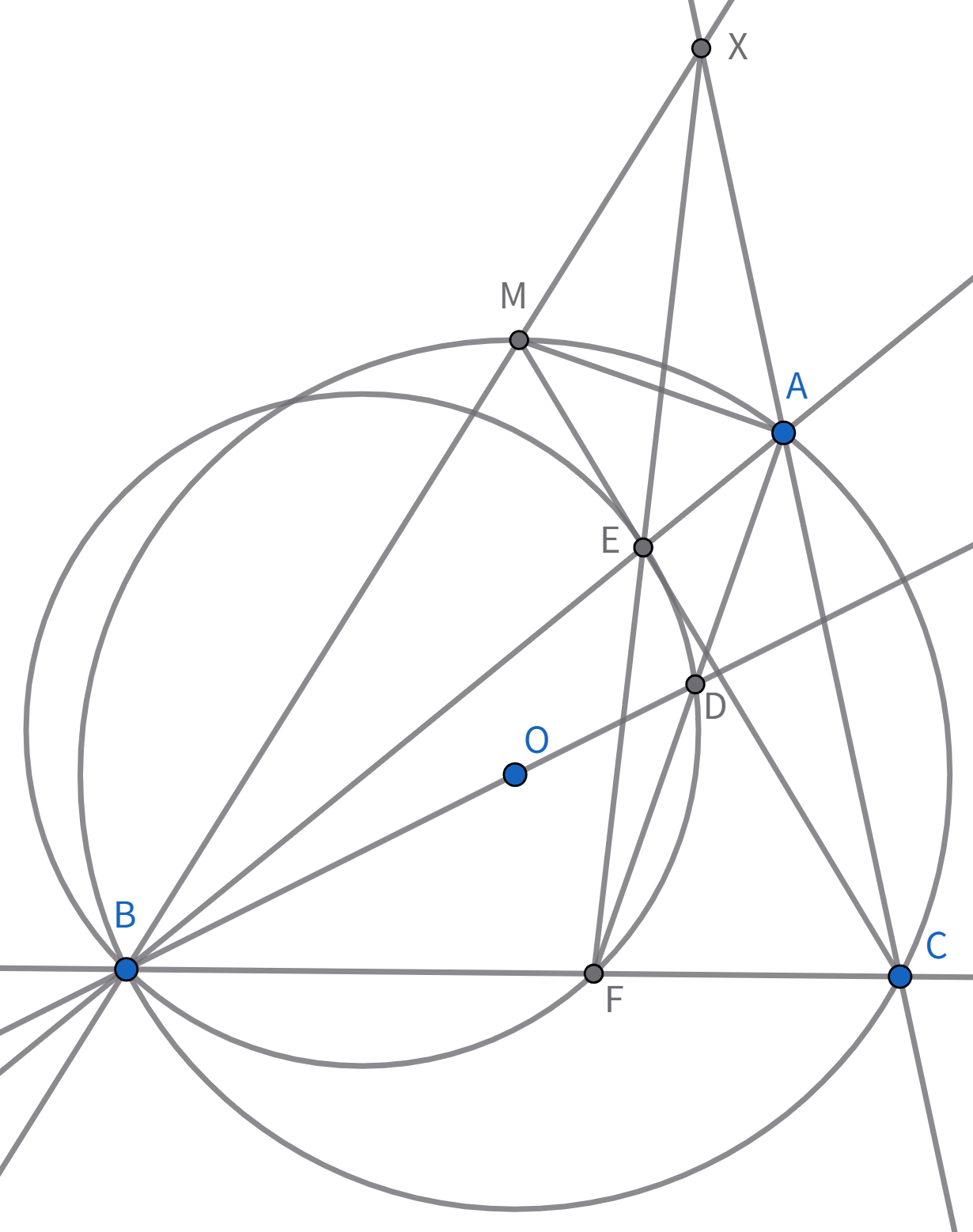
直線$AC$と直線$MB$の交点を$X$とすると, $\angle MAB=\angle MCB=\angle MBC=\angle MAX$より$AX:AB=XM:BM$が成立します. 直線$XE$と辺$BC$の交点を$F$とすると, チェバの定理から
$$ \frac{XA・CF・BM}{AC・FB・MX}=\frac{XA・CF・AB}{AC・FB・XA}=\frac{CF・AB}{AC・FB}=1 $$
が成立し, $BF:CF=AB:AC$なので点$F$が$\angle BAC$の二等分線上すなわち直線$AD$上にあることが分かります.
$\angle ABC=\angle AMC=\angle ADE$より四点$BEDF$は共円です. $\angle AXF+\angle AFX=\angle CAF=\frac{1}{2}\angle BAC=\angle BMO=\angle MBO=\angle ABX+\angle DBE=\angle ABX+\angle DFE$より$\angle AXE=\angle ABX$. 接弦定理から円$BEX$は直線$AX$に接するので方べきの定理から$AE・AB=AX^2, AX=55.$
$XM=55x$とすると$BM=121x, XE=80x$です. さらに, $\angle AXE=\angle ABM=\angle ACE$より$\triangle XEC$は二等辺三角形なので,$CE=XE=80x$であり, $CM=BM=121x$から$EM=41x.$
$\triangle AEC\sim\triangle MEB$なので$AC=121x・\Large\frac{25}{41x}=\Large\frac{3025}{41}.$
特に解答するべき値は$3066$です.

感想

チェバの定理が刺さるのが良いですね. $\angle BAC$の二等分線と直線$BC$の交点を$F'$としたときの三点$XEF'$の共線は比較的証明が楽なのに見えず, しかも更なる応用が利きそうです. 事実, 当コンテスト問題D正解者全員に解法を聞いてみたところ, 誰も気づかなかったらしいです. 証明には他のアプローチもあり, それが解法2です.

(近い未来$OMC$で高度典型として$500$点程で出される可能性もありますね.～)

解法2

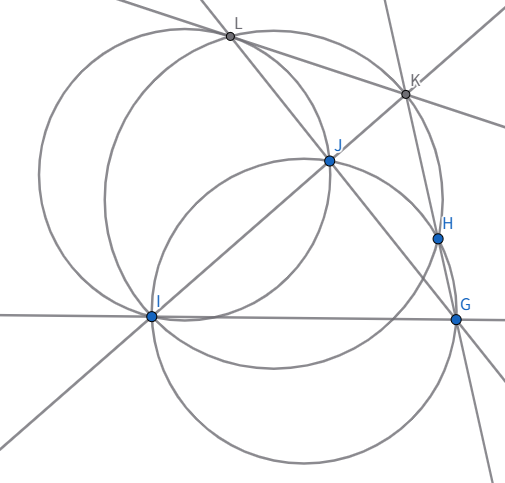
角度追跡から四点$BEDF', ADBX$は共円です. ここで$AD・AF=AB・AE$より円$ABD$と直線$EF'$の反転共役が分かるので点$A$中心半径$\sqrt{AB・AE}$の円での反転を考えると点$X$は不動であり, $AE・AB=AX^2$を示すことができます.
(分からない方は図3のようなイメージを持ちましょう.)

感想

これはコンテストTesterの匿さんから頂いた解法です. 反転を用いたアプローチは筆者も一切想定しておらず頂いた時はかなり驚きました.

最後に

この問題には座標解や地道に角度追跡をするなど他の解法も存在し, 今回挙げたのはその一例にすぎません. しかしその中でもチェバの定理を用いた解法は素晴らしく, Testerや参加者からも好評があったのでこれを想定解として「良問オブザイヤー2026」に投稿してみようかと思ってます. このコンテストは他にも好評が多かった問題があり, この記事を見た方は是非取り組んでみてほしいです. 以上が問題Dの解説でした.