『柏陽祭2025問題E』の解説

はじめに

　2025年末、当コンテストの解説を書き忘れていたことを指摘され、Writerとしての役割を果たしてない現状を不甲斐なく感じながら記事を書いています。この記事では『柏陽祭2025』問題Eの解説をします。
他の問題の記事
『柏陽祭2025』の解説

コンテストサイト

以下のリンクから飛ぶことができます.
柏陽祭2025

問題文

半径が$14$の円$Ω$に内接し, $AB>AC$を満たす鋭角三角形$ABC$について, 内心を$I$, $A$傍心を$J$とする. 辺$AJ$の垂直二等分線と$Ω$の交点の内, 点$C$側にあるものを$D$, $B$側にあるものを$E$とし, 三角形$JBC$の外接円と三角形$JDE$の外接円の交点を$X(\neq J)$としたところ, 以下が成り立った.
$$ CX:CD=8:3,　AI=10 $$
辺$BC$と辺$DE$の交点を$F$としたときの線分$XF$の長さの二乗を求めてください.

解説

$\angle{BAC}$の二等分線と$\Omega$の交点を$M$とすると,トリリウムの定理より四点$BICJ$は点$M$中心の同一円周上にあります.
(この定理は証明を角度追跡のみで終えることができる非常に簡単な定理なので知識として蓄えておくことをお勧めします.)
線分$DE$に関して点$A$と点$J$は対称であるため
$\angle{MJD}=\angle{MAD}=\angle{MCD},MC=MJ$より三点$JDC$は共線.
同様に三点$JBE$も共線です.
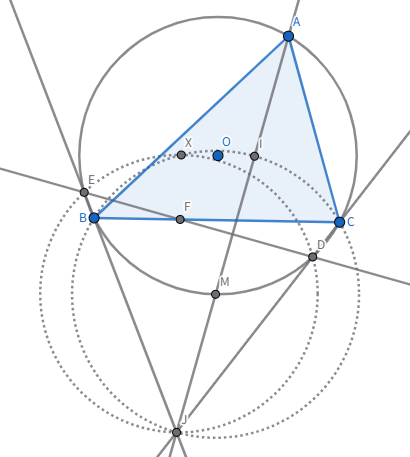長さは正確ではありません
点$F$は円$\Omega$,円$IBC$,円$JDE$の根心なので三点$XFJ$は共線.さらに点$F$は線分$DE$上にあるため$\angle{MXF}=\angle{MJF}=\angle{MAF}$より四点$MAXF$は共円.
また、方べきの定理より${JF}\cdot{JX}={JM}\cdot{JA}={JB}\cdot{JE}={JC}\cdot{JD}$が成り立っています.
線分$AJ$に関して点$B$と対称な点を点$Y$,点$C$と対称な点を点$Z$とすると,$\angle{JXD}=\angle{JED}=\angle{BXJ}=\angle{JXY}$より三点$XDY$は共線(同様に三点$XZE$は共線).
円$\Omega$の中心を$O$とすると$\angle{BOD}=2\angle{BAD}=2\angle{BCD}=\angle{BMJ}$より$\triangle{BOD}\backsim\triangle{BMJ}.$
$\angle{BOD}=\angle{BMJ}=180\degree-2\angle{BJM}=180\degree-\angle{BJY}=\angle{BXD}$より四点$BXOD$は共円.
$\angle{YXI}=\angle{YJI}=\angle{BJM}=\angle{DBO}=\angle{DXO}$より三点$XOI$は共線.
点$D$について, $\angle{MJD}=\angle{MAD}=\angle{MBD}$より, $BD=JD=AD.\angle{MJD}+\angle{CJY}=\angle{MJY}=\angle{MJB}=\angle{OBD}=\angle{OAD}=\angle{MAD}+\angle{IAO}$より$\angle{CJY}=\angle{IAO}.\angle{CXD}=\angle{CJY}=\angle{IAO}=\angle{IMO},\angle{XCD}=\angle{XCJ}=\angle{XIJ}=\angle{MIO}$より$\triangle{CXD}\backsim\triangle{IMO}.$
$IM=8x$とすると, $IO=3x.$ 方べきの定理より$(14-3x)(14+3x)=10\cdot8x.$ これを解くと$x=2$であり,$\angle{OIM}=60\degree$,$IJ=32$であるため$XJ=16\sqrt{3}.$
方べきの定理より$JF\cdot{JX}=JM\cdot{JA}.$これに値を代入させて解くと$JF=14\sqrt{3}.XF=2\sqrt{3}$であるため解答するべき値は$12$.