数理音楽理論における組合せ論覚え書き #1: Rhythmic oddity property

146

この記事は，組合せ論 Advent Calendar 2024 の23日目の記事です．

この記事は，rhythmic oddity property（ROP）についての歴史的なサーベイである．ROPは，アフリカ音楽のリズムパターンに見られるとある性質であるが，数学的には， ${2, 3}^{*}$ に属する語に対して要求される性質として表現される．具体的な定義は後ほど明らかになる．

準備

ここでは，語の組合せ論の基本事項を確認する．

$A$ 上の語の集合を $A^{*}$ と書く．
語 $v, w$ の連結は $v w$ と書く．
空な語は $ε$ と書く．
語 $w$ に対し， $\overset{n}{\overset{⏞}{w \dots w}}$ を $(w)^{n}$ と書き， $w \in A$ のときは $()$ は省略する．
語 $w$ の長さを $| w |$ と書く．
$v \in A^{*}$ が $w \in A^{*}$ の因数／始切片／終切片であるとは， $w = x v y$ ／ $w = v y$ ／ $w = x v$ なる $x, y \in A^{*}$ があることをいう．
$v, w \in A^{*}$ が共役である（ $v \sim w$ ）とは， $v = x y$ かつ $w = y x$ なる $x, y \in A^{*}$ があることをいう．
$v \in A^{*}$ の共役類 $[v]$ とは， ${x \in A^{*} : v \sim x}$ をいう．

以下， $A \subseteq N$ とする．
$w = a_{1} a_{2} \dots a_{| w |} \in A^{*}$ の高さ $h (w)$ とは， $\sum_{i = 1}^{| w |} a_{i}$ をいう．

Arom

民俗学者のSimha Arom (1985)は，中央アフリカ音楽のリズムパターンに，rhythmic oddityと呼ばれる非対称性が頻出することを発見した．ここでは，リズムパターンといえば，ループするリズムパターンのことである．

rhythmic oddityは，中央アフリカの様々な民族・集団の音楽に見られることが指摘されているが，後の研究でもよく取り上げられるのは，Akaの音楽である．Akaは，中央アフリカ共和国南西部～コンゴ共和国北部に分布するピグミーであり，彼らの多声音楽は UNESCO無形文化遺産にも登録されている．

mbenzele

Akaのmbenzeleと呼ばれる音楽には，以下のリズムパターンが現れる．

mbenzeleのリズムパターン．

各音価を自然数で表すと，このリズムパターンは $[22223222223]$ と表すことができる．もちろん，今はループされるリズムパターンのみを考えているので，そのシフト
$\begin{aligned} [22223222223] \\ [2223222223 & 2] \\ [223222223 & 22] \\ ⋮ \\ [3 & 2222322222] \end{aligned}$
も，全て同じリズムパターンであることに注意せねばならない．

mokongo

mokongoと呼ばれる楽器の演奏には，以下のリズムパターンが現れる．
mokongoのリズムパターン．

このリズムパターンは， $[332323332]$ と表せる．

ちなみに，mokongoはこのように木の枝を寝かせて，複数人でばちで叩いて演奏する．
mokongoを演奏するAkaの人々．(Arom 1991/1985)

Aromは，こうしたリズムパターンに，次のrhythmic oddity（原文ではimparité rythmique）なる性質を見る．

rhythmic oddity (Arom, 1985/1991, p. 248)

The technique of rhythmic oddity is based on the principle of progressively inserting binary quantities into configurations bounded by ternary quantities.

(...) an inversion of this principle, by inserting ternary quantities in configurations bounded by binary values.

数学的に書けば，こうなるだろう．

リズムパターン

$A \subseteq N$ とする． $R$ が $A$ 上のリズムパターンであるとは， $R$ がある語 $w \in A^{*}$ の共役類 $[w]$ であることをいう．

rhythmic oddity

${2, 3}$ 上のリズムパターン $R$ がrhythmic oddityを持つとは， $n, m \in N$ を使って，
$R = [\sum_{i = n}^{n + m} 3 2^{i}]$
または
$R = [\sum_{i = n + m}^{n} 2 3^{i}]$
と書けることをいう．
ただし，ここでは文字列の連結を $\sum$ で表記している．

$m = 1$ の場合に前者の生成法を適用すると，
$\begin{aligned} n = 0 : & [3 & 32] & = [332] \\ n = 1 : & [32 & 322] & = [32322] \\ n = 2 : & [322 & 3222] & = [3223222] \\ n = 3 : & [3222 & 32222] & = [322232222] \\ n = 4 : & [32222 & 322222] & = [32222322222] \end{aligned}$
といったリズムパターンを生成できる． $n = 4$ の場合のリズムパターンは，mbenzeleである．

$m = 2$ の場合に後者の生成法を適用すると，
$\begin{aligned} n = 0 : & [233 & 23 & 2] & = [233232] \\ n = 1 : & [2333 & 233 & 23] & = [233323323] \\ n = 2 : & [23333 & 2333 & 233] & = [233332333233] \\ n = 3 : & [233333 & 23333 & 2333] & = [233333233332333] \end{aligned}$
といったリズムパターンを生成できる． $n = 1$ の場合のリズムパターンは，mokongoである．

Chemillier

1999年12月，ヨーロッパ数学会によってIRCAMで開催されたMathematics and Music Diderot Forumの中で，rhythmic oddityの一般的な定式化が，Chemillier (2002)により与えられた．

ROP (Chemillier 2002)

$2, 3$ からなるリズムパターンがrhythmic oddity property（以下，ROP）を満たすとは，それが2等分できないことをいう．

rhythmic oddity propertyという言葉の初出も恐らくここであろう．

数学的に書けば，

ROP

${2, 3}$ 上のリズムパターン $R$ がROPを満たすとは，任意の $w \in R$ と $u, v \in A^{*}$ に対して，次が成り立つことをいう．

$h (w)$ は偶数である．
$w = u v$ ならば $h (u) \neq h (v)$ ．

語 $w \in {2, 3}^{*}$ がROPを満たすとは， $[w]$ がROPを満たすことをいう．

実際，翌年の(Chemillier & Truchet, 2003)でも上記のように定義されている．

mbenzeleのリズムパターン $[22223222223]$ はROPを満たす．実際，このリズムパターンは次のように2分割できるが，いずれの場合も2等分されていない．
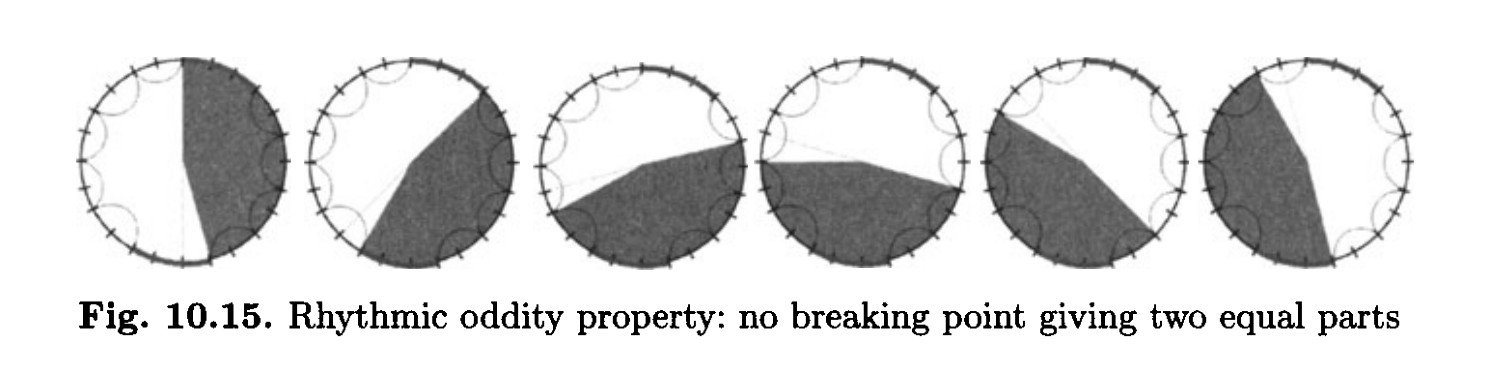mbenzeleのリズムパターンの分割．(Chemillier, 2002)

なお，Chemillierによるこの定義は，Aromによる定義と一致しない．例えば，

$[233232]$ はAromの定義を満たすが，Chemillierの定義は満たさない（ $h (233232) = 15$ は偶数ではないため）．
$[222]$ はChemillierの定義を満たすが，Aromの定義は満たさない（定義3のいずれの生成法でも生成できないため）．

このように，(Chemillier, 2002)は，ROPに対して初めて語の組合せ論的な議論を与えたという意味で重要である．同文献にはROPに関するいくつかの結果が証明なしで書かれている．

次いで，Chemillier & Truchet (2003)は，ROPを満たすリズムパターンの数え上げを行った．その中で証明された主要な結果を挙げる．

$w \in {2, 3}^{*}$ がROPを満たすならば，次のいずれかが成り立つ．

$h (v) = h (u) + 2$ かつ $w = u v$ なる $u, v$ が一意に存在する．
$h (u) = h (v) + 2$ かつ $w = u v$ なる $u, v$ が一意に存在する．

前命題

$u v \in {2, 3}^{*}$ がROPを満たすならば，次のいずれかが成り立つ．

$h (u) = n / 2 - 1$ かつ $h (v) = n / 2 + 1$
$h (u) = n / 2 + 1$ かつ $h (v) = n / 2 - 1$

非対称ペア

$u, v \in {2, 3}^{*}$ とする． $(u, v)$ が非対称ペア（asymmetric pair）であるとは，任意の $u$ の始切片 $u^{'}$ と $v$ の始切片 $v^{'}$ に対して，
$h (u^{'}) \neq h (v^{'}) + 1$
となることをいう．

(Chemillier & Truchet, 2003)

$w \in {2, 3}^{*}$ とする．以下は同値である．

$w$ はROPを満たす．
$h (v) = h (u) + 2$ かつ「 $w = u v$ または $w = v u$ 」となるような，非対称ペア $(u, v)$ が存在する．

まだまだ序盤だが，いったん打ち切りにして，続きはまた今度．（参考文献を順に読めば，ほぼ完全にROP研究の展開を追えると思います．）

参考文献

年順に並べる．

Arom, S. (1985). Polyphonies et Polyrythmies d'Afrique Centrale: Structure et Methodologie. SELAF.
Arom, S. (1991). African Polyphony and Polyrhythm: Musical Structure and Methodology. Cambridge University Press. (Original work published 1985)
Chemillier, M. (2002). "Ethnomusicology, Ethnomathematics. The Logic Underlying Orally Transmitted Artistic Practices". In G. Assayag, H. G. Feichtinger, & J. F. Rodrigues (Eds.), Mathematics and Music: A Diderot Mathematical Forum (pp. 161-183). Springer.
Chemillier, M. & Truchet, C. (2003). Computation of words satisfying the “rhythmic oddity property” (after Simha Arom's works). Information Processing Letters, 86(5), 255-261. https://doi.org/10.1016/S0020-0190(02)00521-5
Hall, R.W. & Klingsberg, P. (2004). Asymmetric rhythms, tiling canons, and Burnside's lemma. In R. Sarhangi & C. H. Séquin (Eds.), Bridges: Mathematical Connections in Art, Music, and Science (pp. 189-194). https://archive.bridgesmathart.org/2004/bridges2004-189.html
Toussaint, G. (2005). Mathematical features for recognizing preference in Sub-saharan African traditional rhythm timelines. In S. Singh, M. Singh, C. Apte, & P. Perner (Eds.), Pattern Recognition and Data Mining. Springer. https://doi.org/10.1007/11551188_2
Chemillier, M. (2007). Les Mathématiques Naturelles. Éditions Odile Jacob.
Chemillier, M. (2009). Mathématiques de la musique en Afrique centrale. CultureMATH. http://cm2.ens.fr/content/mathematiques-de-la-musique-en-afrique-centrale-2073
Bouchet, A. (2010). Imparité rythmique. Culturemath. http://cm2.ens.fr/maths/articles/Bouchet2010/imparite-rythmique.html
Toussaint, G.T. (2013). The Geometry of Musical Rhythm: What Makes a "Good" Rhythm Good?. CRC Press.
Jedrzejewski, F. (2017). Counting words satisfying the rhythmic oddity property. arXiv:1607.07175v2
Jedrzejewski, F. (2017). New investigations on rhythmic oddity. In O. Agustín-Aquino, E. Lluis-Puebla, & M. Montiel, (Eds.) Mathematics and Computation in Music: MCM 2017 (pp. 227-237). Springer. https://doi.org/10.1007/978-3-319-71827-9_17
Boenn, G. (2018). Computational Models of Rhythm and Meter. Springer.
B. Srečko, C. Marc & R. Christophe (2018). Music and combinatorics on words: a historical survey. Journal of Mathematics and Music, 12(3), 125-133. https://doi.org/10.1080/17459737.2018.1542055
Brlek, S., Chemillier, M. & Reutenauer, C. (2018). Music and combinatorics on words: a historical survey. Journal of Mathematics and Music, 12(3), 125-133. https://doi.org/10.1080/17459737.2018.1542055
Jedrzejewski, F. (2024). A Compendium of Musical Mathematics. World Scientific.