テンソルネットワークで紡ぐ宇宙~3.MERAからBHへ~

1. MERAからブラックホールへ

前回の最終章で取り上げたMERAというテンソルネットワークは、長距離の相関を取り入れるために、短距離の相関を効果的に取り除くようなディスエンタンギュラーを内部に取り込んだ形式になっていました。エンタングルメントをきちんと記述できる理論としてMERAは非常に重要な構造をもっていました。
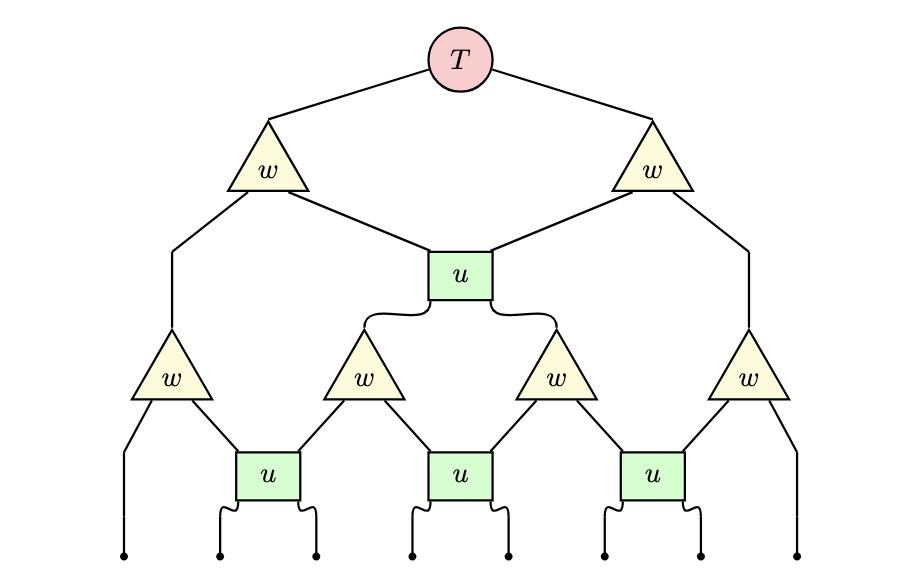MERAの図
では、この考え方を推し進めて連続極限（cMERA）に適用するとどうなるでしょうか？ 絶対零度の真空であれば、私たちはどこまでも無限にズームアウトし続けることができます。つまり、時空は無限の彼方まで続いていきます。
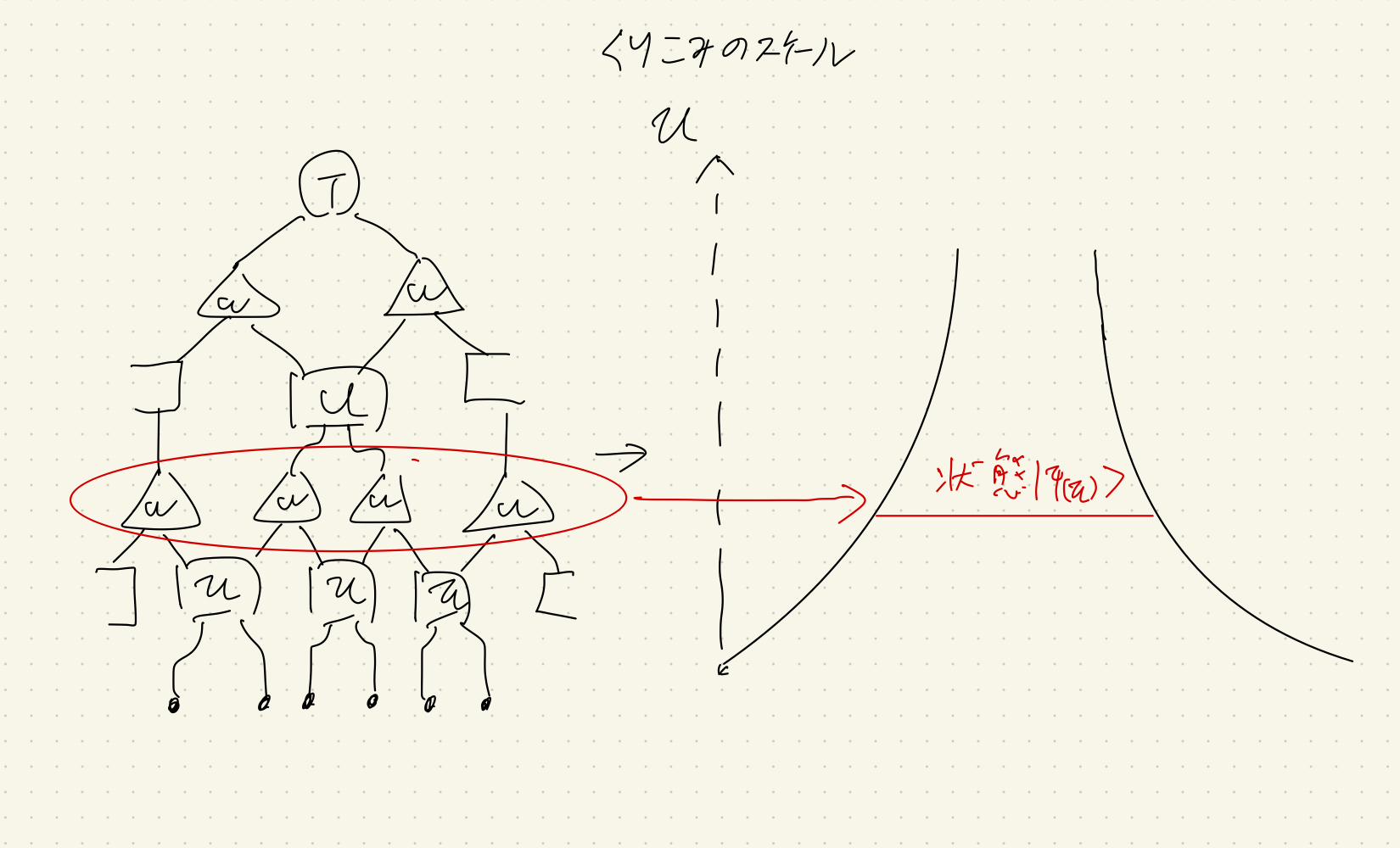cMERAのイメージ図。状態のある空間とくりこみが連続的になり、始まりと終わりがなくなっている
今回のメインテーマは、このcMERAが持っている幾何学的構造が、とあるタイプの宇宙論と対応しているというお話です。テンソルネットワークが物性理論を飛び出し、一般の場の理論に対する強力な表現となっていることを実際に見ていこうと思います。
今回は取り上げる内容が濃いので、先に流れを整理しておこうと思います。

• まずは今回の舞台となるAdS時空について、一般相対性理論の観点から簡単にレビューを行いたいと思います。

• その後cMERAの描像からAdS時空の計量が計算できることを示し、テンソルネットワークとAdS時空の等価性を見ます。

• 最後に、有限温度のAdS時空がテンソルネットワークにおいて何に対応するのか、その時くりこみの果てで何が起こっているのかを見ていこうと思います。

1. 重力理論とAdSブラックホール

ミンコフスキー計量$\eta_{\mu\nu}$について、非対角成分は$0$、インデックス$0$の時を$-1$、それ以外を$1$として扱います。

1.1 アインシュタイン方程式と宇宙定数

今回は基礎的な一般相対論に関する内容は吹っ飛ばして、アインシュタイン方程式から始めようと思います。

この方程式の意味合いをざっくり述べれば、左辺$R$は空間の曲がり具合を、右辺$T$は空間のエネルギーを表しており、エネルギーのあるところは曲がり具合が強くなるよ〜くらいのことを行っています。
ここで1人だけ今の説明の中になかった$\Lambda$というタームは何を表しているのでしょうか？これがいわゆる宇宙定数と言われる値です。この部分は、数学的な導出の際に結果に影響を及ぼさないために出てくる自由度ですが、現代の宇宙物理学ではここの部分がある種の"真空"におけるエネルギーのように思うことができ、ダークエネルギー等を記述する部分になっていると考えられています。
今ここの値が負であると思うことにすると、それは左辺の曲がり具合の項に最初から何かしら負の値が存在することになります。これによって空間全体が負の曲率、つまり双曲的な幾何学を張ることが予想できます。このような空間では、宇宙は膨張するのではなく、むしろ内側に引き込まれるようになります。
AdS時空のイメージ図
ではこんなものを考えて何が嬉しいのでしょうか？その答えは宇宙が一つの閉じた系として扱えるようになるからです。曲率が非負の物理学においては宇宙が膨張していくため、真空中で一度放たれた物体はどこまでもとんでいくことができます。例えばブラックホールにおけるホーキング放射はその一例で、そのために厳密にはブラックホールは非平衡系であったりします。
一方で宇宙定数が負の時空においては、空間のエッジが明確であり、その外側に要素が逃げていってしまうことがないので、様々な物理的考察をする場として適しています。今から登場するAdS時空も、このような宇宙定数が負である時空の一種であることについて後で触れます。

1.2 AdS時空の幾何学

まず、ホログラフィーの舞台となる $d+2$ 次元の Anti-de Sitter (AdS) 時空 について、その計量から様子を探っていきましょう。

基本の計量

これをポアンカレ座標という座標系に変換します。
$z=\frac{l^2}{X^{-1}+X^{d+1}},x^\mu=\frac{1}{l}X^{\mu}z$
これを使うとAdS時空における線素は以下のように書けます。 $$ ds^2 = \frac{l^2}{z^2} \left(dz^2 + \eta_{\mu\nu}dx^{\mu}dx^{\nu}\right) $$
ここでこの$z$という方向はざっくりエネルギースケールを表しており、極限で以下のように振舞います。
境界 ($z \to 0$): $z$ がゼロに近づくと、$\frac{1}{z^2}$ は無限大になります。つまり、ここでは距離の尺度が無限に細かくなります（UV極限）。この端に$d+1$次元の境界が存在します。

バルク ($z > 0$): 重力が働く内部の世界です。$z$ が大きくなることはMERAの深いところまで進行することになりますが、これはどんどん低エネルギーの極限を見ていくことに対応します。

宇宙定数を計算してみよう

ここで、少し計算をして時空の宇宙定数 $\lambda$ が負になることを確かめてみましょう。 真空のアインシュタイン方程式は先ほど表示したように以下の形をしています。
$$ R_{\mu\nu} - \frac{1}{2}R g_{\mu\nu} + \lambda g_{\mu\nu} = 0 $$
この式に、先ほどのAdS計量を代入して計算してみましょう。

1. リッチテンソル $R_{\mu\nu}$ の計算
   今回のAdS時空はあらゆる点・あらゆる方向で曲率が一定です。（このような空間を最大対称性を持つと言ったりします。）
   このような空間において、リーマン曲率テンソル $R^{\lambda}_{\rho\mu\nu}​$ は、その対称性から以下の形に一意に定まることが知られています。
   $$ R^{\lambda}_{\rho\mu\nu}​=K(g^{\lambda}_{\mu}g_{\rho\nu}-g^{\lambda}_{\nu}g_{\rho\mu}) $$
   ここで$K$は空間の曲率で、今の場合は$-\frac{1}{l^2}$をとります。
   リッチテンソル$R_{\rho\nu}​$​は、リーマンテンソルの添字を一つ縮約することで定義されます。
   $$ R_{\rho\nu}​=g^{\mu}_{\lambda}R^{\lambda}_{\rho\mu\nu} =K(g^{\mu}_{\lambda}g^{\lambda}_{\mu}g_{\rho\nu}-g^{\mu}_{\lambda}g^{\lambda}_{\nu}g_{\rho\mu}) ​$$
   ここで、2つの項をそれぞれ評価します。
   まず第一項は計量のトレース$g^{\mu}_{\lambda}g^{\lambda}_{\mu}$なので、その空間の次元$D$になります。 今回の場合、$AdS_{d+2}$ なので、次元は $D=d+2$ ですね。
   次に第二項はクロネッカーのデルタ$g^{\mu}_{\lambda}g^{\lambda}_{\nu}$なので
   $g^{\mu}_{\lambda}g^{\lambda}_{\nu}g_{\rho\mu}=g_{\rho\nu}$
   になります。
   以上をまとめると、リッチテンソルは
   $$ R_{\rho\nu}​=\left( -\frac{d+1}{l^2} \right) g_{\rho\nu} $$
   となり、計量に比例することがわかりました。
2. スカラー曲率 $R$ の計算
   リッチテンソルの縮約を取ります。時空の次元は $D = d+2$ であることに注意して計算します。 $$ R = g^{\mu\nu} R_{\mu\nu} = (d+2) \times \left( -\frac{d+1}{l^2} \right) = -\frac{(d+1)(d+2)}{l^2} $$
   となります。
3. アインシュタイン方程式へ代入
   最後にこれらを方程式の左辺に代入しましょう。
   $$ \begin{aligned} &R_{\mu\nu} - \frac{1}{2}R g_{\mu\nu}+\Lambda g_{\mu\nu} \\ &= -\frac{d+1}{l^2} g_{\mu\nu} - \frac{1}{2} \left( -\frac{(d+1)(d+2)}{l^2} \right) g_{\mu\nu}+\Lambda g_{\mu\nu}\\ &= \frac{d+1}{l^2} \left[ -1 + \frac{d+2}{2} \right] g_{\mu\nu}+\Lambda g_{\mu\nu} \\ &= \frac{d(d+1)}{2l^2} g_{\mu\nu}+\Lambda g_{\mu\nu}\\ &=0 \end{aligned} $$
   ここから
   $$ \Lambda = - \frac{d(d+1)}{2l^2} $$
   となり、AdS計量がアインシュタイン方程式を満たすためには、宇宙定数 $\lambda$ は必ず負の値でなければならないことが導かれました！

1.2 BTZブラックホールと温度

では、このような不思議な空間における、ブラックホールの解を考えるとどうなるでしょうか？
一旦話を簡単にするために、$d=1$の$AdS_3$におけるブラックホールを考えていきましょう。毎度お馴染みのアインシュタイン方程式を書き下すと、以下のようになります。
$$ R_{\mu\nu} - \frac{1}{2}R g_{\mu\nu} + \Lambda g_{\mu\nu} = 0 , \Lambda = -\frac{1}{l^2} $$
ブラックホールが出てくるということはそれすなわち計量が発散するポイントになるので、これが生成する計量テンソルを考えてみましょう。まずは以下のような座標変換を考えます。
$$ X^{-1}=\sqrt{\frac{r^2}{M}}\cosh(\sqrt{M}\phi) $$
$$ X^0=\sqrt{\frac{r^2}{M}-l^2}\sinh(\frac{\sqrt{M}t}{l}) $$
$$ X^1=\sqrt{\frac{r^2}{M}-l^2}\cosh(\frac{\sqrt{M}t}{l}) $$
$$ X^2=\sqrt{\frac{r^2}{M}}\sinh(\sqrt{M}\phi) $$
これがAdS時空の式$ -(X^{-1})^2+\eta_{\mu\nu}X^{\mu}X^{\nu}+(X^{d+1})^2=-l^2$を満たしていることはすぐにわかります。
簡単のため、今回転については考えないことにして$ds^2=-(dX^{-1})^2+\eta_{\mu\nu}dX^{\mu}dX^{\nu}+(dX^{d+1})^2$に代入して頑張って計算をしていくと、
$$ dX^{-1}=dr\frac{1}{\sqrt{M}}\cosh(\sqrt{M}\phi)+d\phi r\sinh(\sqrt{M}\phi) $$
$$ dX^2=dr\frac{1}{\sqrt{M}}\sinh(\sqrt{M}\phi)+d\phi r\cosh(\sqrt{M}\phi) $$
$$ dX^0=dr\frac{r}{M\sqrt{\frac{r^2}{M}-l^2}}\sinh(\frac{\sqrt{M}t}{l})+dt\sqrt{\frac{r^2}{l^2}-M}\cosh(\frac{\sqrt{M}t}{l}) $$
$$ dX^1=dr\frac{r}{M\sqrt{\frac{r^2}{M}-l^2}}\cosh(\frac{\sqrt{M}t}{l})+dt\sqrt{\frac{r^2}{l^2}-M}\sinh(\frac{\sqrt{M}t}{l}) $$
となるので
$$ ds^2=-(-M+\frac{r^2}{l^2})dt^2+\frac{1}{-M+\frac{r^2}{l^2}}dr^2+r^2d\phi^2 $$
と出すことができます。
この計量が発散するのは$-M+\frac{r^2}{l^2}=0$の時なので、$r=\sqrt{M}l$が事象の地平面になります。
このような$(2+1)$次元のブラックホールをBTZブラックホールと言います。
AdS時空に関する説明を終わる前に、最後にBTZブラックホールの温度を考えておきましょう。ここでは細かいことは省略しつつ、wick回転によって（虚）時間と（逆）温度が対応することを素直に認めて話を進めます。
wick回転$it\to \tau$を行うと
$$ ds^2=(-M+\frac{r^2}{l^2})d\tau^2+\frac{1}{-M+\frac{r^2}{l^2}}dr^2+r^2d\phi^2 $$
となります。発散に寄与する項について事象の地平面付近で展開を行うと
$$ ds^2\sim\frac{2r(r-r_H)}{l^2}d\tau^2+\frac{l^2}{2r(r-r_H)}dr^2 $$
となります。ここで$R=2\sqrt{\frac{l^2(r-r_H)}{2r}}$と変数変換すれば
$$ ds^2\sim R^2\left(\frac{r}{l^2}\right)^2d\tau^2+dR^2 $$
となります。これは二次元での極座標と形式が酷似しており、
$d\theta=\frac{r}{l^2}d\tau$とすることによって方位角方向とみなすことができます。
あとは、自然に入る周期境界条件を考えてあげれば$\tau$の周期$\beta$について
$\beta=\frac{2\pi l^2}{r}$
が得られるので、
$T=\frac{1}{\beta}=\frac{r}{2\pi l^2}\to\frac{\sqrt{M}}{2\pi l}$
となります。最後の矢印で事象の地平面に極限を取りました。簡単な形ではありますが、これでBTZブラックホールの温度が求まりました。

　蛇足ですが、この温度はシュバルツシルトブラックホール等の温度よりもある意味で厳密です。最初にもお話しした通り、AdS時空は閉じた系だとみなすことができ、蒸発が起こりません。そのため、熱力学的にはある種の定常状態になっているのです。一方、通常のブラックホールの温度も緩和の時間スケールを考えれば十分定常状態と見做せるので、そこまで問題にはならないと思います。

また$M$というのは質量=エネルギーのスケールを持った値であり、$r$が小さい=低エネルギー有効理論において効果が効いてきます。この辺をわかっていると、この後の理解が簡単になると思います。

2. cMERAから創発する時空

創発という言葉は近年の物理学で幅広く用いられる言葉ですが、その本意は局所的な少数系を見ているだけでは分からない非自明な現象が、巨視的な多体系で現れることを表しています。
今から見ていくのは、前回の記事の最後で紹介したMERAを連続化した cMERA (continuous MERA) を用いた場の量子論の解釈です。前回の記事ではMERAについて、空間的なくりこみを再帰的に行っていくという説明をしました。これをある種の"時間発展"とみなして連続化させていくことによって、単一では見えなかった新たな幾何的構造が創発する様子を見ていこうと思います。

2.1 cMERAの定義

離散的なMERAは、波動関数を効率的に表現し、その長距離相関を抽出する強力な手法でした。これを場の量子論（連続系）に適用できるよう拡張したものが cMERA (continuous MERA) です。
ここではMERAが、どのようにして滑らかなcMERAへと変貌するのか、その対応関係を明確にしながら定義を行います。

"時間発展"する系の特徴

MERAでは、粗視化のステップを層状にとして積み重ね、これによってくりこみを行っていきました。cMERAでは、この層の厚みを極限まで薄くした連続パラメータ $u$ を導入します。これをくりこみ群のスケールパラメータと呼びます。
前回の記事でも述べていた通り、MERAは長距離の相関を取り出すことを得意としていて、CTMRGやDMRGで収束の悪かった臨界系を記述することに長けています。
このような臨界系は、一般にスケール変換に対する不変性を持ちますが、ここにローレンツ不変性や相互作用の制約を課すことで、自然に共形不変性に拡張することができます。
今回はこのcMERAの最下層の部分が共形不変性を持つような場の理論（共形場理論）に従うと考えて、計算を行っていきましょう。
今回、共形場理論に関しては詳しく扱わないことにしました。理由は単純で、導入にあまりにもスペースを取る割に、計算で必要な場面が数回しかないからです。今回は共形場理論特有の性質を用いるところでは、都度定性的な説明を入れようと思います。詳しく知りたい方は専門書を見てみてください。

　以下ではくりこみ群のフローを表す$u$方向への計算を"時間発展"と言うことにします。

操作の連続極限

MERAの1ステップでは、アイソメトリーとディスエンタンギュラーを用いて粗視化を行っていましたね。cMERAでは、この1ステップを連続パラメータの微小な変化 $du$ とみなします。これによってそれぞれの操作は、波数空間における連続的な生成子で表現できるようになります。

1. アイソメトリー $W \to$ スケール変換 $L$
   離散系では2サイトを1つにまとめる ことで粗視化を行いました。しかし、連続的な場では点を減らすことはできないので、適切な領域を粗視化した上で座標全体を拡大するという操作を行います。これがスケール変換の生成子 $L$ です。

2. ディスエンタンギュラー $U \to$ 相互作用 $K(u)$
   ディスエンタンギュラーは近接サイト間の相互作用によってエンタングルメントを解く効果を持っていました。これを$K(u)$と表すことにします。注意点としては近接サイトのみに効果を及ぼすようにしないと意味がないので、実空間でも波数空間でも適切な領域に絞る必要があります。

これらを組み合わせると、微小なスケール $du$ だけ進める操作は、以下のように書けます。
$$ \ket{\Psi(u+du)} \approx e^{-i L du} \cdot e^{-i K(u) du} \ket{\Psi(u)} \approx e^{-i (K(u) + L) du} \ket{\Psi(u)} $$
連続化されたくりこみ（"時間発展"）の様子

状態の構成式

上記の微小操作を、IR極限（$u_{IR}$）から高エネルギー領域（$u=0$）まで無限回積み重ねることで、状態 $\ket{\Psi(u)}$ が得られます。
$$ \ket{\Psi(u)} = \mathcal{P} \exp \left( -i \int_{u_{IR}}^{u} (K(s) + L) ds \right) \ket{\Omega} $$
ここで$\mathcal{P}$は経路順序積です。
しかしこのままでは二つの生成子が混ざって複雑です。そこで、量子力学の相互作用描像のように、スケール変換の効果だけを分離した状態 $\ket{\tilde{\Psi}(u)}$ を定義します。
$$ \ket{\tilde{\Psi}(u)} \equiv e^{iuL} \ket{\Psi(u)} $$
この座標系、つまりスケールとともに拡大するフレームから見てみると、状態の変化はディスエンタンギュラー $\hat{K}(u)$ だけで記述されます。
$$ \frac{d}{du} \ket{\tilde{\Psi}(u)} = -i \tilde{K}(u) \ket{\tilde{\Psi}(u)} $$
ここで、$\tilde{K}(u) \equiv e^{iuL} K(u) e^{-iuL}$ です。

2.2 計量の導入

以上の描像では、cMERAの縦方向に、スケール変換$u$というある種の時間座標のようなものを入れた形として見えていました。これに対して何かしらの幾何学を考えたいとなれば、そこに計量を入れようと思うのは自然な発想です。
今、異なる$u$を持つ層は、異なる量子状態を表しています。量子情報理論には、量子状態間の距離を測る自然な尺度である Bures距離 があるので、これをスケールの違う二つの状態の比較に使ってあげることを考えましょう。
$$ G_{uu}(u) du^2 \equiv 1 - |\braket{\Psi(u)}{\Psi(u+du)}|^2 $$
これを $du$ について2次まで展開すると、量子フィッシャー情報量 が現れます。以下の式を見ればわかるように、演算子 $\tilde{K}(u)$ がアイデンティティなら$0$になってしまうので、$\tilde{K}(u)$の作用の非自明度合いを表していると解釈することができます。
$$ G_{uu}(u) = \langle{\tilde{\Psi}(u)}|{\tilde{K}(u)^2}|{\tilde{\Psi}(u)}\rangle - \left|\langle{\tilde{\Psi}(u)}|{\tilde{K}(u)}|{\tilde{\Psi}(u)}\rangle\right|^2 $$

2.3 自由スカラー場におけるAdS計量の導出

実際にAdS時空の計量が得られるのか、具体的なモデルで計算してみましょう。
最も基本的なCFTのモデルである、$d$ 次元空間上の質量ゼロの自由スカラー場を考えます。

モデルとディスエンタングラーの設定

ハミルトニアンは、生成消滅演算子 $a_k, a_k^\dagger$ を用いて以下のように書けます（真空エネルギーは無視します）。 $$ H = \int d^dk \, |k| \, a_k^\dagger a_k $$ この系に対して、cMERAのディスエンタングラー $K(u)$ を構成します。自由場の場合、ガウス状態の性質を保つ必要があるため、$K(u)$ は粒子の対生成・対消滅を表すスクイージング演算子の形をとります。 $$ K(u) = i \int d^dk \, \chi(k, u) \left( a_k a_{-k} - a_k^\dagger a_{-k}^\dagger \right) $$ ここで $\chi(k, u)$ は、どの運動量スケールでどれくらい強くエンタングルメントを切るかを決める実数の変分パラメータです。先ほど書いたようにMERAの物理的要請から、この関数はカットオフ運動量 $\Lambda$ 付近でのみ値を持つような形状をしています。

実空間では超近距離に対応しますね

計量の計算プロセス

前節で導入したフィッシャー情報量 $G_{uu}(u)$ を計算します。これは相互作用描像における演算子 $\tilde{K}(u)$ の分散（ゆらぎ）に相当します。
$$ G_{uu}(u) = \langle{\tilde{\Psi}(u)}|{\tilde{K}(u)^2}|{\tilde{\Psi}(u)}\rangle - \left|\langle{\tilde{\Psi}(u)}|{\tilde{K}(u)}|{\tilde{\Psi}(u)}\rangle\right|^2 $$
ここで、相互作用描像の演算子 $\tilde{K}(u) = e^{iuL} K(u) e^{-iuL}$ を具体的に書き下してみましょう。生成子 $L$ は空間を適当なスケーリングで $e^u$ 倍に拡大する操作に対応するため、運動量は $k \to k e^{-u}$ へと縮小されます。これに伴い、積分測度と演算子は以下のように変換則に従います。

1. 積分変数の変換: 物理的な運動量 $k$ を、スケール不変な運動量 $\tilde{k}$ に書き換えます。 $$ k = \tilde{k} e^u \quad \Longrightarrow \quad d^dk = e^{du} d^d\tilde{k} $$
2. 演算子の変換: 交換関係 $[a_k, a_{k'}^\dagger] = \delta(k-k')$ を保つため、演算子は積分演算子の変換を打ち消すように変換されます。 $$ e^{iuL} a_k e^{-iuL} = e^{-du/2} a_{\tilde{k}} $$ これらを $K(u)$ の定義式に代入すると、以下のようになります。
   $$ \begin{aligned} \tilde{K}(u) &= i \int (e^{du} d^d\tilde{k}) \, \chi(\tilde{k}e^u, u) \left[ (e^{-du/2} a_{\tilde{k}}) (e^{-du/2} a_{-\tilde{k}}) - \dots \right] \\ &= i \int d^d\tilde{k} \, \chi(\tilde{k}e^u, u) \left( a_{\tilde{k}} a_{-\tilde{k}} - a_{\tilde{k}}^\dagger a_{-\tilde{k}}^\dagger \right) \end{aligned} $$ 積分測度から出る $e^{du}$ と、演算子のペアから出る $e^{-du}$ が完全にキャンセルしました！これはスケール部分だけを見るとデルタ関数とやっていることが同じなので、交換関係側の要求が生きた形になります。残る $u$ 依存性は変分パラメータ $\chi$ の中身だけです。

最適解と定数計量の出現

ここで、ハミルトニアンの期待値を最小化するような最適解 $\chi(k, u)$ を考えます。 対象としている系はCFTであり、スケール不変性を持ちます。そのため、最適なカットオフ関数 $\chi$ の形状は、カットオフ $\Lambda e^u$ に対する比率 $k / (\Lambda e^u)$にのみ依存する形になります。
$$ \chi(k, u) = F\left( \frac{k}{e^u} \right) = F(\tilde{k}) $$ つまり、$\tilde{k}$ 空間で見れば、波形 $F(\tilde{k})$ は $u$ に依存せず一定不変です。 これを計量の式に代入して積分を実行します。 $$ G_{uu}(u) \propto \int d^d\tilde{k} \, |F(\tilde{k})|^2 = \text{const} $$ 被積分関数が $u$ に依存しないため、その積分結果も当然定数になります。この定数を $L_{AdS}^2$ と置くことで、AdS計量のスケール成分が導かれます。 $$ ds_{scale}^2 = L_{AdS}^2 du^2 $$

cMERAから創発する時空

以上の結果をまとめましょう。

• スケール方向: 今計算した通り、$ds_{scale}^2 = L^2_{AdS} du^2$。
• 空間方向: 生成子 $L$ の定義により空間は $e^u$ 倍されるため、$ds_{space}^2 = e^{2u} (dx^2)$。

これらを合計すると、cMERAから創発する時空の全計量は以下のようになります。 $$ ds^2 = L^2_{AdS} du^2 + e^{2u} \sum_{i=1}^d dx_i^2 $$ 最後に、座標変換 $z = L_{AdS} e^{-u}$ （$dz = -z du$）を行えば、 $$ ds^2 = \frac{L^2_{AdS}}{z^2} \left( dz^2 + \sum_{i=1}^d dx_i^2 \right) $$ となり、AdS時空の計量が、場の量子論の変分原理から厳密に導出されました。

　ここで「時空側がミンコフスキー計量になってないじゃん」と思われた方もいると思いますが、その通りです。今は本当の意味での時間発展を考えていないので、時間の軸は除いて議論しています。そう思うと最初に計算した式と対応しているのがわかると思います。

3. AdS/CFT対応

2章では、物理的な状態を$(1+1)$次元のCFTにおいて、そこからMERAを展開した時に、AdS時空の計量が出てくることを見ました。このような対応関係を一般にAdS/CFT対応と呼びます。

この対応が重要になる所以は、AdS時空という直感的でない空間のダイナミクスを、重力のない量子場の理論という比較的扱いやすい理論体系の中で見ることができる点です。エンタングルメントエントロピーの解析や、物性理論と弦理論の様々な橋渡しとしてみることができるAdS/CFT対応ですが、せっかくなのでここでは今まで見てきたテンソルネットワークによって定性的な解釈を試みてみましょう。（ここから先は割と持論なので、もし明確な間違いがあれば指摘いただきたいです。）
最初の記事で何度も強調して出てきたのが、時間と空間の対応関係でした。分配関数を計算するための空間方向に広がるテンソルネットワークの一軸を、時間発展だと解釈することによって、量子古典対応やDMRGとCTMRGの関係性を見てきました。
今回のCFTとAdSも同じように考えることができます。CFTという量子場のダイナミクスが、重力理論であるとはいえ、AdS時空という古典空間のバルクの性質によって表現できていることがわかります。今までの図と比べてみると以下のように整理できます。
今まで出てきた対応とのアナロジー
以上の話からcMERAがAdS/CFT対応を表現する優れた模型であることを感じ取ってもらえたかと思います。最後の章ではこのcMERAのくりこみのフローを途中で切ってしまった時に何が起こるのかを考え、そこからBTZブラックホールを見出していこうと思います。

詳しい方はお気づきかと思いますが、上記の議論は全てラージN極限での話になっています、有限自由度系においてはAdS側も量子揺らぎの効果が無視できないので、単純な比較は難しくなります。

4. 有限温度とブラックホール

4.1 RGフローの停止

まずは以下のようにくりこみ群を途中で止めた系を考えましょう。cMERAには普通周期境界条件が入るので、以下のようなドーナツ状になります。
ドーナツ型のcMERA。座標の取り方の対応関係に注意。$l$は中心から出ているように書いていますが、実際は至る所で曲率半径は$l$で同じです。
この系は"時間発展"としては有限の時間発展に相当しますが、分配関数としてはどうでしょうか。時間発展演算子$e^{i\hat{H}t}$に相当する項は$e^{-\beta\hat{H}}$でしたから、模型の等価性を加味すると$t$が有限ということはすなわち$\beta$が有限であるということを意味します。つまりこれは有限温度系$T>0$を表したcMERAと解釈できるわけです。
くりこみのスケールは温度である

4.2 BTZブラックホールとの対応

以上のような途中でくりこみが止まった系における計量を考えてみましょう。
$$ ds^2 = \frac{l^2}{z^2} \left( dz^2 + \sum_{i=1}^d dx_i^2 \right) $$

$L_{AdS}$はくどいので$l$にしてしまいました。

今座標変換座標変換 $z = l e^{-u}$を行っていたことを思い出してあげると、$z$方向というのはすなわち有限温度$\beta$に当たるので、ここから
$$u\sim\log(lT)$$
が言えます。
次に遠方を見た時にcMERAの変数変換前の線素とBTZの変数変換後の線素で比較を行います。
$$ ds^2 = l^2 du^2 + e^{2u} \sum_{i=1}^d dx_i^2 $$
$$ ds^2=-(-M+\frac{r^2}{l^2})dt^2+\frac{1}{-M+\frac{r^2}{l^2}}dr^2+r^2d\phi^2 $$
先ほど少し触れた通り遠方=高エネルギー領域では$M$は無視できるので
$$ ds^2=-(\frac{r^2}{l^2})dt^2+\frac{1}{\frac{r^2}{l^2}}dr^2+r^2d\phi^2 $$
ここから空間成分に注目すると、今$d\phi$は曲率中心から見た角度を指しているので、cMERA側での方向成分$dx$との対応関係は
$$ld\phi=dx$$
となります。そうなると、$d\phi^2$と$dx^2$の間の対応関係として
$$ e^{2u}=\frac{r^2}{l^2} $$
が得られ、先ほどの結果を用いると
$$ T=\frac{r}{l^2}\sim \frac{\sqrt{M}}{l} $$
となり、BTZブラックホールから直接出した温度とスケールが一致しました。これらの結果はcMERAとBTZブラックホールが同じ計量、同じ温度を持つ模型であることを表しています。
これによって有限で打ち切ったcMERAからBTZブラックホールを作ることができました。

5 終わりに〜イジング模型からブラックホールへ〜

いかがでしたでしょうか。最初はイジング模型の転送行列から始まったテンソルネットワークによって、ブラックホールを表現するところまで、早足にはなりましたが見ていくことができました。前回はコードで書けばかなり面倒くさいアルゴリズムを扱いましたし、今回も真面目に検討しようと思えば非常に難しい重力理論に対して、テンソルネットワークの力を大いに使って豊かな帰結を得ることができました。テンソルネットワークの良いところを3つの記事を通じてたくさんお見せすることができたのではないかなと思います。
余裕があればまた番外編として、量子誤り訂正符号との関係性にフォーカスした記事を作成しようと思っています。気長にお待ちください。ここまで見ていただきありがとうございました！
ありがとう！