文献あり

近畿大学数学コンテストA-5の組合せ的解釈

はじめに

MARTHさんがtwitter上で問題提起した近畿大学数学コンテストA-5の組合せ解釈を募集するツイートについて
立見鶏さんの記事を参考にしながら、
$\displaystyle\sum_{k=0}^{n-1}(-1)^k {} _ {3n-2k} \mathrm{C} _ {n-1-k} \times {} _ {2n-k} \mathrm{C} _ {k} $ の組合せ解釈による証明を思いついたので証明します。

誤植や誤りなどがあればリプかtwitterのdmにて教えてくださると嬉しいです

証明

3色のボールの塗分けに言い換える

${} _ {3n-2k} \mathrm{C} _ {n-1-k} \times {} _ {2n-k} \mathrm{C} _ {k}$ は以下のように言い換えられる。

$3n-2k$個の一直線上に並んだ白いボールを $2n-k+1$ 個のボールのグループ$P$と $n-1-k$ 個のボールのグループ$Q$に分ける。
グループ$P$のうち一番右にあるボールをボール$X$とし、それ以外の$2n-k$個のボールをグループ$P'$とする。
グループ$P'$の$2n-k$個のボールを$2n-2k$個のボールのグループ$R$と$k$個のボールのグループ$S$に分ける。

ここでグループ$Q$のボールを青色に、グループ$R$のボールとボール$X$を白のままに、グループ$S$のボールを赤に塗る。

またこれは以下のように言い換えられる
$3n-2k$個の一直線上に並んだ白いボールを$k$個の赤いボール、$ n-k-1$個の青いボール、$2n+1-2k$個の白のままのボールに塗り分けるが、どの赤いボールよりも右側に白いボールが存在するようにする。

例えば図1の上の塗分け方は条件を満たすが、下は一番右の赤玉より右に白玉が存在しないため条件を満たさない。
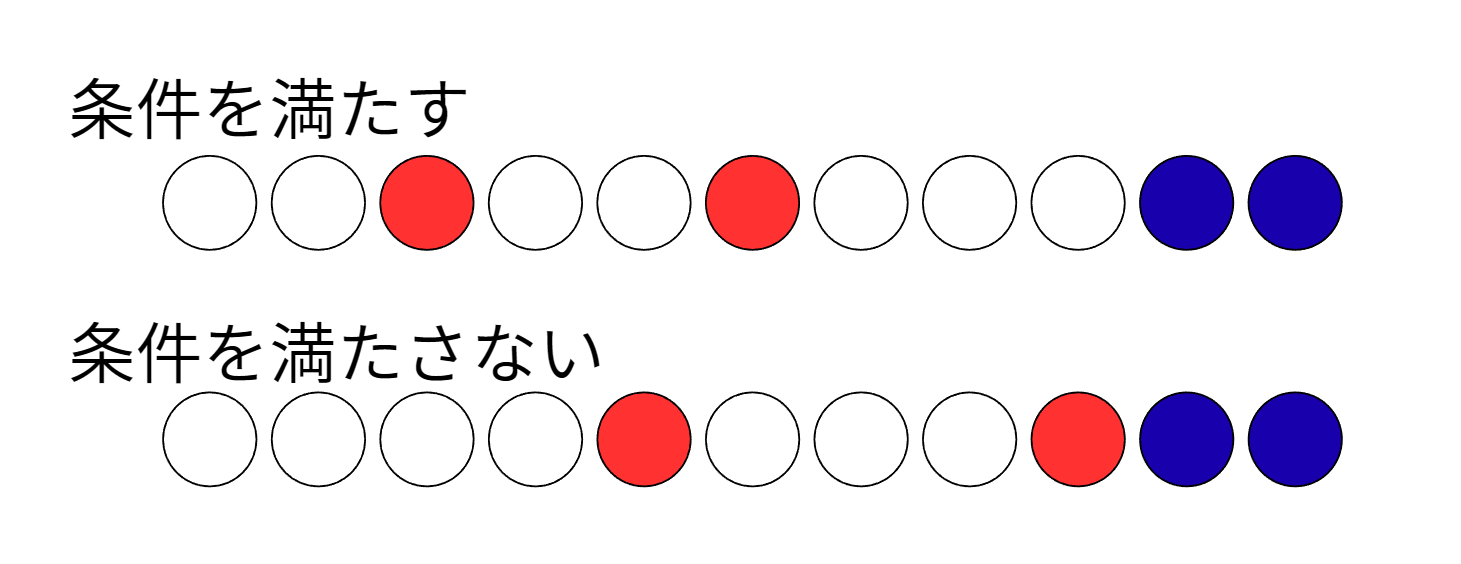例n=5 k=2

3色のボールの塗分けを2色のボールの塗分けに言い換える

$3n$個の白いボールが一直線上に並んでおり、左から2個ずつのペア$n-1$個と、残りのペアになっていない$n+2$個のボールがある。ペアを右から順に$A_1,A_2,...,A_{n-1}$とする。

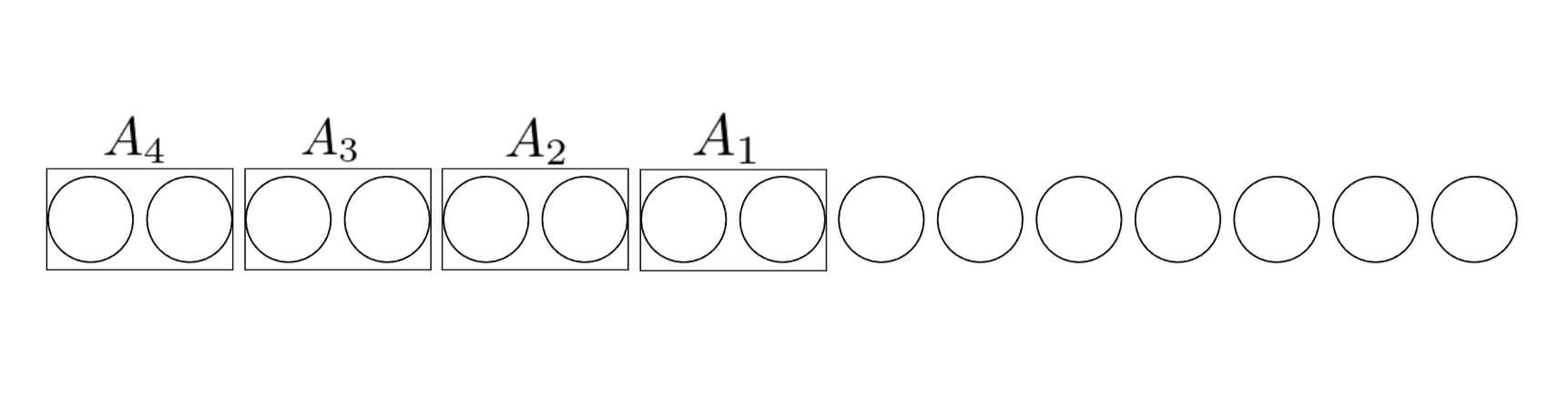例n=5 例n=5

この時、以下のように$3n-2k$個のボールの3色(白,赤,青)への塗分けと$3n$個のボールの2色(白,黒)への塗分けを対応させる。

・$3n-2k$個のボールのうち赤または青に塗ったボールを右から順番に$1,2,...n-1$と番号を付け、赤で塗られたボールとそれに対応したペアをロックし、彩色不可能にする。（ボール$i$が赤色ならペア$A_i$）を彩色不可能にする。(下の画像ではそのグループを×にしている)
・彩色不可能なペアを除くことで残った$3n-2k$個のボールを左から順番に、赤色又は青色で塗られたボールを黒色に、白色なら白色のままにする。

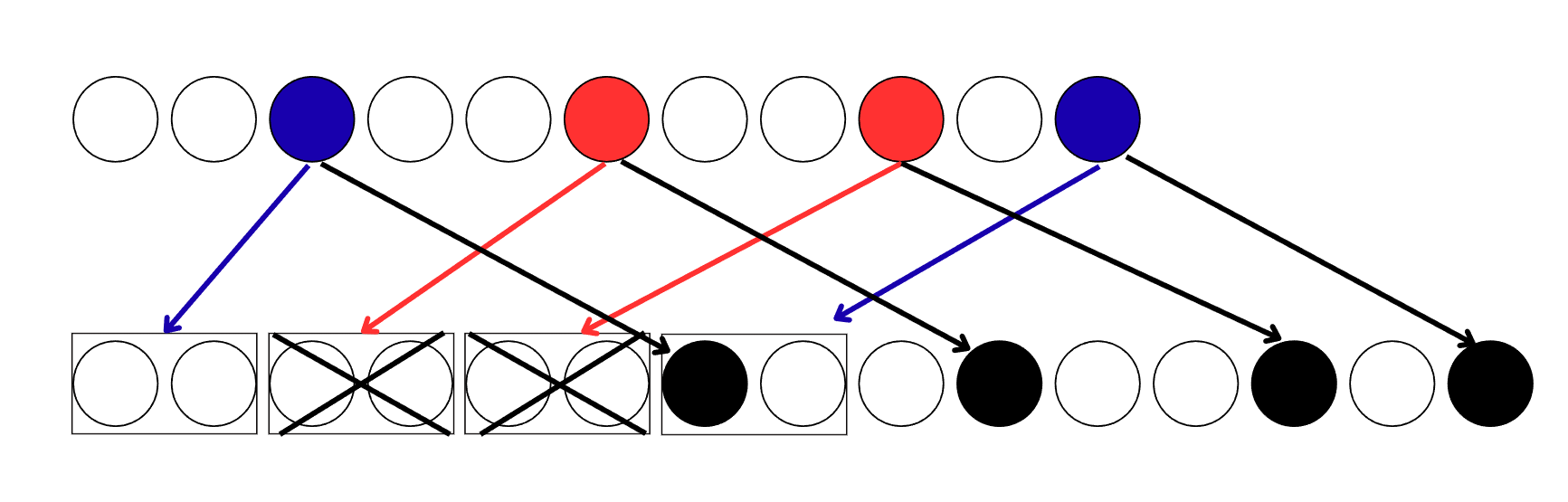例 n=5 k=2 青,赤矢印はペアを彩色不可能にするか。黒線は色の対応を表している。×は彩色不可能

場合分けと包除原理

場合分け

”3色の塗分け”と”2色の塗分けとグループの彩色可否”に対応させることができた。一旦3色の塗分けに戻って場合分けをしてみる。

$n$の値は固定し、$k$を自由に決められるすべての事象において、青玉が一番右から最大いくつ連続しているかで場合分けする。一番右から青玉が$i$個連続している事象の集合を$B_i(i=0,1,...,n-1)$とする。
下の画像は上から順に$B_0,B_1,B_2,B_3,B_4$の一つである。
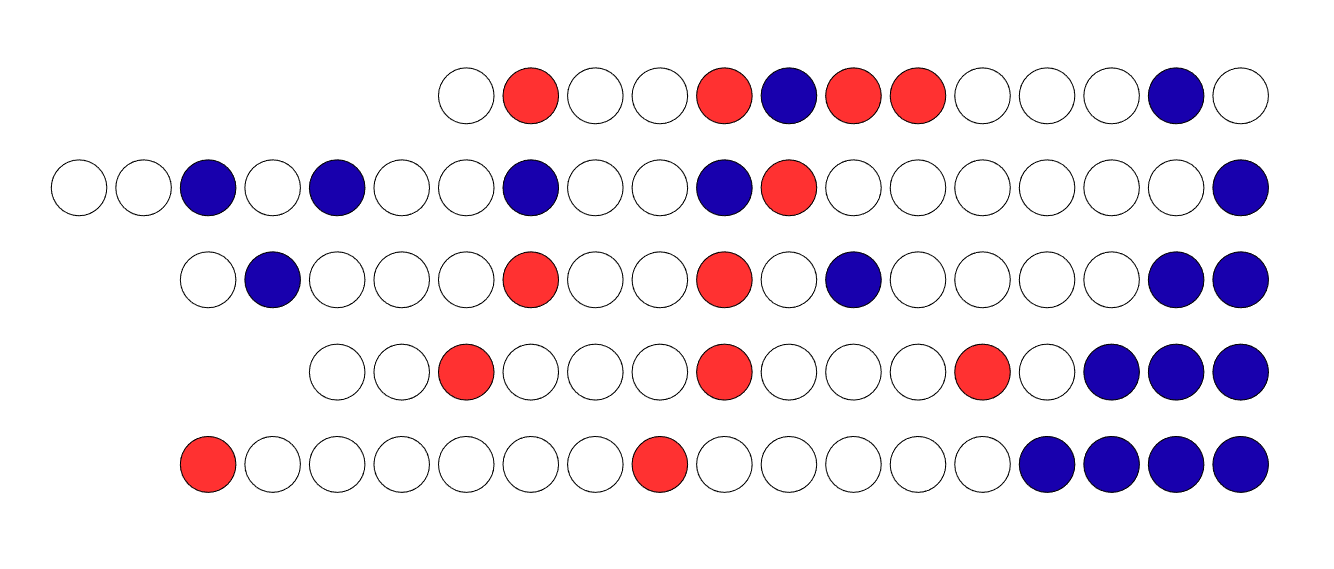n=7 n=7

事象$B_i$における赤玉の数(元の式のkの値)を$k$とした時、塗分けの組合せの数を$f(i,k)$とする、そうすると$\displaystyle\sum_{i=0}^{n-1}\displaystyle\sum_{k=0}^{n-1-i}(-1)^kf(i,k)$が求める答えである。

$\displaystyle\sum_{k=0}^{n-1-i}(-1)^kf(i,k)$を包除原理を使って求める。

ペア$A_j$が彩色不可能であり、右からちょうど$t$個の玉が黒に塗られている事象を$C_{j,t}$とすると、$\displaystyle\sum_{k=0}^{n-1-i}(-1)^kf(i,k)=\displaystyle\sum_{i+1 \leq a \leq n-1}|C_{a,i}| - \displaystyle\sum_{i+1 \leq a < b \leq n-1}|C_{a,i} \cap C_{b,i}| + \displaystyle\sum_{i+1 \leq a < b< c \leq n-1}|C_{a,i} \cap C_{b,i} \cap C_{c,i}|- ...$

であり、これは包除原理でグループ$A_{i+1}$～$A_{n-1}$それぞれから一つずつ黒に塗られて、右から$i$個のボールを全て黒にする塗り方の組合せを求めているものである。
これはグループ$A_{i+1}$～$A_{n-1}$から黒に塗るボールを一つずつ選択すればよいので$2^{n-1-i}$である。