ソリトンと古典可積分系

$$ \newcommand{\df}[1]{\dfrac{\partial}{\partial {#1}}} \newcommand{\dff}[1]{\dfrac{\partial^2}{\partial {#1}^2}} $$
［本記事はPhysics Lab. Advent Calender2026の18日目の記事です。］
はじめまして、東京大学理学部物理学科（内定）2年のmakkuroymmnです。今回は、ソリトンと古典可積分系について見ていきたいと思います。自然界は「波」で溢れています。身近な自然現象だけでも、水面を伝わる波、音、光、楽器の弦の振動など非常に多くの「波」があります。ソリトンとはもともと水面を伝わる波の観察から見出された特殊な性質を持つ非線形の波です。このソリトンの性質を概観するのが一つ目の目標です。もう一つのトピックが、古典可積分系とソリトンの関係です。可積分系とは、平たく言えば「運動方程式をきちんと積分して解を求められるような系」のことです。実はこれはソリトンと深い関係にあり、本稿ではその部分にも少し踏み込めたらと思います。それではよろしくお願いします。

（ pdf版はこちら。 ただし波のアニメーションはpdfに載せられなかったのでこのサイトのものを参照してください。）

線形波動と非線形波動---KdV方程式とソリトン---

本章では、Korteweg-de Vries (KdV)方程式という非線形の波動方程式について説明します。KdV方程式の解にどのようなものがあるかを調べ、ソリトンとは何かを見ていければと思います。

はじめに---線形の波動方程式---

皆さんは波動方程式をご存じでしょうか。波動方程式とは、音や光、弦の振動など、自然界においてもっともよく現れる方程式の一つで、$x$軸方向に速さ$c$で伝わる1次元の波を表す波動方程式は以下のようになります。

波動方程式$(1)$は
\begin{equation} u = f(x \pm ct) \tag{2} \end{equation}
の形の解をもちます。これは、$(1)$を
\begin{equation} \left(\df{t}-c\df{x}\right)\left(\df{t}+c\df{x}\right) u = 0 \tag{3} \end{equation}
のように書けば明らかです。例えば
\begin{equation} \left(\df{t}+c\df{x}\right) u = 0 \tag{4} \end{equation}
をみたす $u=f(x-ct)$ を考えれば、これは$(1)$の解にもなっています。
$(2)$の$-$符号は $x$ 軸正方向、$+$ の符号は $x$ 軸負方向に進む波を表します。例えば、$(1)$には
\begin{equation} u = a \sin(kx - \omega t), \quad k=\frac{2\pi}{\lambda}, \quad \omega=2\pi \nu, \quad \frac{\omega}{k}=c \tag{5} \end{equation}
のような解があります。これは$x$正方向に進む三角波ですね。ただし$a$は定数です。
$(1)$の特徴として、$u$について線形になっているということが挙げられます。これは、$u_1,\,u_2$がそれぞれ$(1)$の解であれば$u_1+u_2$も$(1)$の解になっている（重ね合わせの原理）ということを意味します。これは線形の波動方程式にしかない特徴で、今後登場する、KdV方程式をはじめとした非線形な波動方程式でこの性質が成り立たないことはすぐに見て取れることでしょう。

分散項と非線形項

$(4)$に$\alpha u_{xxx}$という三階微分の項を加えた次の方程式を考えます。

この方程式にも、前節で考えた方程式と同じ形の解があります。実際、$u = a \sin(kx - \omega t)$ とおくと
\begin{equation} \frac{\omega}{k} = c - \alpha k^{2} \tag{7} \end{equation}
のときに解になっていることがわかります。ここで重要なのが、前節の場合は波数$k$によらず波の伝わる速さ$\omega/k$が定数$c$であったのに対し、$\omega/k$が$k$に依存しているということです。これは異なる波数の波が異なる速さで進むことを示し、このような性質は分散性と呼ばれます。
次に、$(4)$に非線形項$\beta u u_{x}$を加えた以下のバージョンを考えてみましょう。

$c=\beta=1,\,u + 1\rightarrow u$ として書き直せば
\begin{equation} u_{t} + u u_{x} = 0 \tag{9} \end{equation}
のように簡単に書けます。この方程式に対しては重ね合わせの原理が成立しないことは明らかでしょう。次に、これは
\begin{equation} u = f(x - ut) \tag{10} \end{equation}
の形の解をもつことが代入により確かめられます。この解は$x$軸方向へ「速さ」$u$で進む波を表しますが、これはどのようなことを意味するのでしょうか。実は、$t=0$ で $(x_{0}, \,u_{0})$ の点は
$u_{0} = f(x - u_{0}t) = f(x_{0})$ より時刻$t$には $(x_{0} + u_{0}t,\, u_{0})$ へ移りますから、この解は$t=0$の波形の上部ほど右へ大きく移動する、つまり波が「突っ立って」くるという現象を表しているのです。
このように、波動方程式に分散項や非線形項を入れると一般に元の性質は保たれず、時間発展とともに波形が崩れるといった特異な現象が生じてきます。

KdV方程式

では、分散項と非線形項を両方入れた次のような形の方程式を考えてみましょう。この方程式はもともとD.J.KortewegとG.de Vriesによって浅水波（波長に比して波の存在する部分の水深が十分浅いような波）の方程式として考案されたもので、KdV方程式と呼ばれます。

方程式の係数について：
係数の6が不自然に思えるかもしれませんが、この方程式は$u,\,x,\,t$の適切な尺度変換により係数を任意に変えることができるので本質的な違いはありません。ここでは計算の都合上このように係数を選びました。

$(11)$は以下の形の解を持つことが示せます（証明は省略します）。これは孤立波（$u=\sin(kx-\omega t)$のように周期的な波が連なった形ではなく、一つの山がぽつんと局在してそれが形を保って移動していく解のこと）と呼ばれます。

これにはいくつか別の表現があって、
\begin{equation} u = 2 \dff{x} \log(1 + e^{\pm 2(kx - 4k^{3}t + \delta)}),\quad u = 2 \dff{x} \log\cosh(kx - 4k^{3}t + \delta) \tag{13} \end{equation}
などとも書けます。図1に$(12)$のプロットを示します。これが孤立波であることが見て取れると思います。 KdV方程式の1ソリトン解
次に、$(12)$の解を拡張して、孤立波を2つ含むような別の解（2ソリトン解）を見ていきましょう。やや天下りですが、$(12)$をにらんで
\begin{equation} u = 2 \dff{x} \log \psi(t) \tag{14} \end{equation}
\begin{equation} \psi(t) = 1 + a_{1}e^{-2\eta_{1}} + a_{2}e^{-2\eta_{2}} + a_{3}e^{-2(\eta_{1}+\eta_{2})} \tag{15} \end{equation}
\begin{equation} \eta_{i} = k_{i}x - \beta_i t + \delta_{i} \quad (i=1,2) \tag{16} \end{equation}
とします。$(11)$に代入して
\begin{equation} \beta = 4k_{i}^{3},\,a_{3} = \frac{(k_{1}-k_{2})^{2}}{(k_{1}+k_{2})^{2}}a_{1}a_{2}\quad{(i=1,\,2)} \tag{17} \end{equation}
ならば$(11)$が満たされることがわかります。$\delta_1,\,\delta_2,\,a_1,\,a_2$は任意定数です。
KdV方程式の2ソリトン解
この解のプロットを図2に示します。これは2つのソリトンの衝突を示す解になっています。すなわち、$t\to \pm\infty$でこの解は2つのソリトンに分離しており、衝突の前後でその形を不変に保っているのです。$0< k_1< k_2,\,\delta_1=\delta_2=0$のとき、$t\to \pm\infty$での波形はそれぞれ以下のように表されます。
\begin{align} t \to -\infty: \quad u &\sim \sum_{i=1,\,2} 2k_{i}^{2} \operatorname{sech}^{2}(k_{i}x - 4k_{i}^{3}t + \delta_{i}^-)  \\ t \to +\infty: \quad u &\sim \sum_{i=1,\,2} 2k_{i}^{2} \operatorname{sech}^{2}(k_{i}x - 4k_{i}^{3}t + \delta_{i}^+) \tag{18} \end{align}
ただし
\begin{align} \delta_1^-&=\dfrac{1}{2}\log a_1\\ \delta_1^+&=\dfrac{1}{2}\log a_1+\log\dfrac{k_2-k_1}{k_2+k_1}\\ \delta_2^-&=\dfrac12\log a_2+\log\dfrac{k_2-k_1}{k_1+k_2}\\ \delta_2^+&=\dfrac12\log a_2 \tag{19} \end{align}
です。衝突の前後で2つのソリトンの波形は変化しませんが、位相が変化していることに注目してください。このような現象は線形の波動方程式の解の重ね合わせでは起こりえません。このように、空間内に局在する孤立波が形を変えずに伝播し、それらが衝突の前後で互いの形を変えずに保つ場合に、それらを粒子的な性質を持った波ということでソリトン(soliton)と呼ぶのです。2ソリトン解を次のように書くこともできます。

これを一般化することでソリトンを$N$個含むような$N$ ソリトン解を以下の形で書くことができます。

Nソリトン解でもソリトン同士の衝突が記述されますが、2ソリトン解同様、衝突前後でソリトンの形は不変になります。図3に3ソリトン解のプロットを示します。
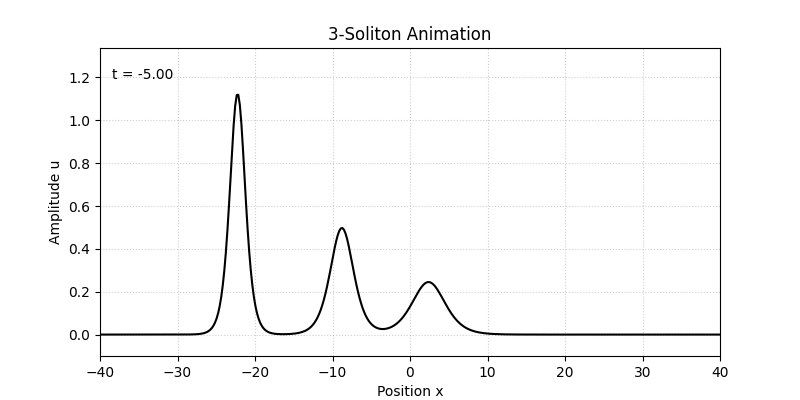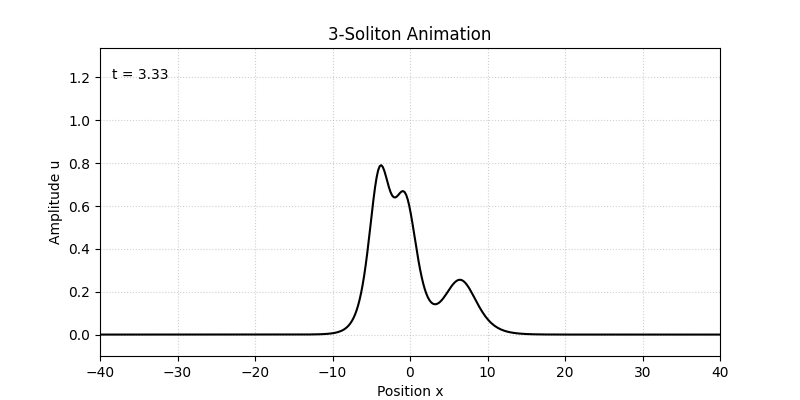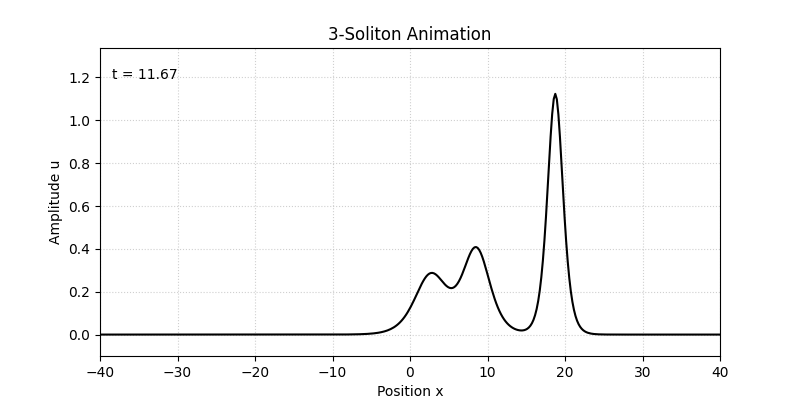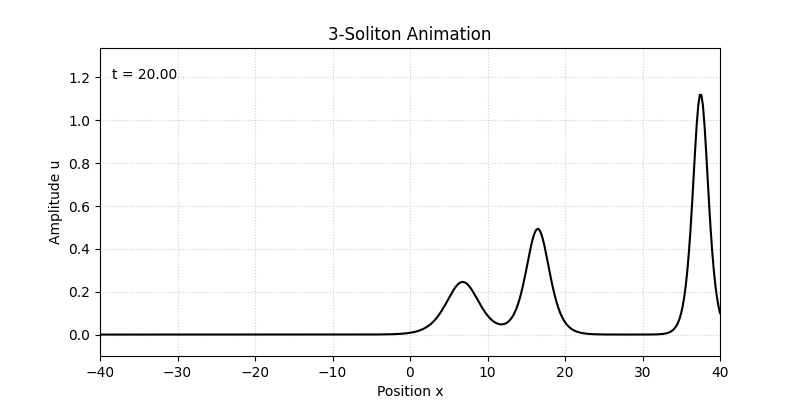KdV方程式の3ソリトン解

ソリトンと可積分系---戸田格子との関係、保存量について---

ここまでKdV方程式のソリトン解についてみてきました。本稿では詳しく解説できなかったのですが、実は、KdV方程式は逆散乱法と呼ばれる手法で初期値問題を解くことができることが知られています。これは力学的にいえばKdV方程式で定まる系が可積分系であることを示します。可積分系とは系の運動方程式を解析的に積分できるような系のことで、Liouvilleの定理によってこれは「系の自由度の数と同じだけの保存量があり、それらがポアソン可換であること（すなわち任意の2つの保存量どうしのポアソン括弧がゼロであること）」と同値です。KdV方程式は場に対する方程式ですから連続無限個の自由度を持ちます。従って、KdV方程式には無限個の保存量が存在するべきであることが結論付けられ、これを実際に確認することを本章の目標としたいと思います。また、有限自由度の代表的な可積分系の一つである戸田格子についても述べ、戸田格子とKdV方程式の類似、とくに戸田格子の運動方程式から連続体近似によってKdV方程式を導けることも見ていきたいと思います。これはKdV方程式が可積分であることの厳密な証明ではありませんが、少なくとも直観的な理解を与えてくれます。

戸田格子

戸田格子とは周期的境界条件を満たすように配置された$N$個の質点が相互作用しているような模型で、そのハミルトニアンは以下のようにして与えられます。

これによって定まる正準方程式は以下のようになります。
\begin{equation} \dot{q}_i = p_i, \quad \dot{p}_i = \exp(q_{i-1} - q_i) - \exp(q_i - q_{i+1}) \tag{26} \end{equation}
ここで，$a_i = \frac{1}{2}\exp \frac{q_i - q_{i+1}}{2}$, $b_i = \frac{1}{2}p_i$
と変数変換すればこれは
\begin{equation} \dot{a}_i = a_i (b_i - b_{i+1}), \quad \dot{b}_i = 2(a_{i-1}^2 - a_i^2) \tag{27} \end{equation}
と簡単な形になります。かなり天下りに思えるかもしれませんが、ここで対称行列 $L$ と反対称行列 $B$ を
\begin{equation} B := \begin{pmatrix} 0 & -a_1 & 0 & \cdots & 0 & a_N \\ a_1 & 0 & -a_2 & \ddots & & 0 \\ 0 & a_2 & \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & -a_{N-2} & 0 \\ 0 & & \ddots & a_{N-2} & 0 & -a_{N-1} \\ -a_N & 0 & \cdots & 0 & a_{N-1} & 0 \end{pmatrix} \tag{28} \end{equation}
\begin{equation} L := \begin{pmatrix} b_1 & a_1 & 0 & \cdots & 0 & a_N \\ a_1 & b_2 & a_2 & \ddots & & 0 \\ 0 & a_2 & \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & a_{N-2} & 0 \\ 0 & & \ddots & a_{N-2} & b_{N-1} & a_{N-1} \\ a_N & 0 & \cdots & 0 & a_{N-1} & b_N \end{pmatrix} \tag{29} \end{equation}
と定めれば運動方程式は

と表されます。
ここでみたような運動方程式の表現をLax表示といいます。この表現から、$L$の全ての固有値が第一積分（保存量）になることが以下の命題によって保証されます。証明は参考文献cite:1p.411などを参照してください。

上記の一般的な定理により、$L$ の $N$ 個の固有値が第一積分になることがわかります。また、$L$の異なる固有値はポアソン可換になっています：
\begin{equation} \{ \lambda, \mu \} = 0. \tag{31} \end{equation}
実際，規格化された $\lambda, \mu$ の固有ベクトル $u, v$ と内積 $(\cdot, \cdot)$ を用いれば
\begin{equation} \lambda = (u, L u) \tag{32} \end{equation}
\begin{equation} \frac{\partial \lambda}{\partial p_i} = \frac{1}{2}u_i^2, \quad \frac{\partial \lambda}{\partial q_i} = u_{i+1}u_i a_i - u_i u_{i-1} a_{i-1} \tag{33} \end{equation}
となることが示せて、$\lambda \neq \mu$ ならば
\begin{equation} \begin{split} \{ \lambda, \mu \} &= \frac{1}{2(\lambda - \mu)} \sum_i \left\{ (v_i u_{i+1} - u_i v_{i+1})^2 a_i^2 - (u_i v_{i-1} - v_i u_{i-1})^2 a_{i-1}^2 \right\}\\ &=0 \end{split} \tag{34} \end{equation}
となります。よって、Liouvilleの定理より、系は完全可積分になります。

KdV方程式のLax形式

KdV方程式に対しても、戸田格子と同じようなLax表示が可能です。KdV方程式を
\begin{equation} u_{t} - 6uu_{x} + u_{xxx} = 0 \tag{35} \end{equation}
とします。第２項の符号が$(11)$と異なりますが、KdV方程式の各項の係数は適当な尺度変換による自由度があるので、元の形と本質的には何も変わりありません。ここでは計算の都合上このように係数を選びました。かなり天下りに思えるかもしれませんが（ｳﾁもﾎﾝﾏにそう思う！！（涙））、次のように作用素$L,\,B$を定めます。
\begin{align} L &= -\partial_{x}^{2} + u \\ B &= -4\partial_{x}^{3} + 6u\partial_{x} + 3u_{x} \tag{36} \end{align}
これを用いれば、KdV方程式$(35)$は

となります。前節でLax形式が系の可積分性と密接に結びついていることを見ました。KdV方程式に対するLax表示が可能であることは、KdV方程式が可積分であることの証明ではありませんが、少なくとも戸田格子との類似性を示唆しているとは言えるでしょう。なお、$L$ の固有値方程式は
\begin{equation} L\varphi = \lambda\varphi \tag{38} \end{equation}
\begin{equation} (-\partial_{x}^{2} + u)\varphi = \lambda\varphi \tag{39} \end{equation}
となっていて、Schrödinger方程式に似ているので、
KdV方程式に付随する Schrödinger方程式といわれます。詳細な説明は略しますが、この固有関数は逆散乱法で重要な役割を果たします。

戸田格子とKdV方程式

ここまで、戸田格子とKdV方程式の両方にLax表示が存在することを見ました。本節では戸田格子とKdV方程式の関係をより深く理解するため、戸田格子の運動方程式から連続体近似を用いてKdV方程式を導出してみましょう。
戸田格子の運動方程式$(26)$は以下のように書くことができます。
\begin{equation} \ddot{r}_{n} = 2e^{-r_{n}} - e^{-r_{n-1}} - e^{-r_{n+1}} \tag{40} \end{equation}
ここで
\begin{equation} e^{-r_{n}} - 1 = \dot{s_{n}} \quad (\text{または } r_{n} = -\log(1+\dot{s_{n}})) \tag{41} \end{equation}
と変数変換すれば、
\begin{equation} \frac{d}{dt}\log(1+\dot{s_{n}}) = s_{n-1} + s_{n+1} - 2s_{n} \tag{42} \end{equation}
元の運動方程式$(26)$の右辺が座標$r$について非線形だったのに対し、この方程式の右辺は新変数$s$に対して線形になっています。これはもとの戸田格子に対して双対格子を考えたことに対応します。なお、$S_{n}=\dot{s_n}$で$S_n$ を定めれば、$S_{n} = \log \psi_{n}(t)$ などとしてKdV方程式と同様の解析が可能で、ソリトン解を求めることができます。このあたりの話題はcite:2に詳しいです。
以降は、改めて $\dot{s_{n}} = f_{n}$ と書きなおした以下の方程式から出発します：
\begin{equation} \frac{d^{2}}{dt^{2}}\log(1+f_{n}) = f_{n-1} + f_{n+1} - 2f_{n} \tag{43} \end{equation}
ここで $0 < h \leq 1$ として $t = \tau/h^{3}$, $f_{n} = h^{2}u_{n}(\tau)$ として書き直すと
\begin{equation} \frac{d^{2}}{d\tau^{2}}\log(1+h^{2}u_{n}) = \frac{1}{h^{4}}(u_{n-1} + u_{n+1} - 2u_{n}) \tag{44} \end{equation}
さらに、
\begin{equation} x = nh - (h^{-2} - h^{2})\tau \tag{45} \end{equation}
と座標変換します。これは速さ $h^{-2} - h^{2} > 0$ で正方向に動く座標に移ることに対応します。計算すると、
\begin{equation} \left\{\df{\tau} - (h^{-2} - h^{2})\df{x}\right\}^2 \log(1+h^{2}u(x,\,\tau)) \tag{46} \end{equation}
\begin{equation} = \frac{1}{h^{4}}[u(x+h,\,\tau) + u(x-h,\,\tau) - 2u(x,\,\tau)] \tag{47} \end{equation}
パラメーター$h=1$のときは戸田格子に帰着します。ここで、$h \to 0$ の極限を考えて、$h^{2}$ 以上の項を無視すると、
\begin{align} \text{左辺：}\quad &-2\partial_{x}\partial_{\tau}u + h^{2}\partial_{x}^{2}u - \frac{1}{2}\partial_{x}^{2}u^{2} \tag{48}\\ \text{右辺：}\quad &\frac{1}{h^{2}}\partial_{x}^{2}u + \frac{1}{12}\partial_{x}^{4}u \tag{49} \end{align}
\begin{equation} \partial_{x}(-2\partial_{\tau}u - \frac{1}{2}\partial_{x}u^{2}) = \frac{1}{12}\partial_{x}^{4}u \tag{50} \end{equation}
遠方で $u(x,\tau) \to 0$ とすれば
\begin{equation} u_{\tau} + \frac{1}{2}uu_{x} + \frac{1}{24}u_{xxx} = 0 \tag{51} \end{equation}
となり、これは適当な尺度変換によりKdV方程式と一致します。

KdV方程式の無限個の保存量

最後に本節では、KdV方程式が無限個の保存量を持つことを、実際に保存量を構成することで確認していきましょう。本章の最初にも述べましたが、KdV方程式が可積分であることの直接的な証明は初期値問題を解く手法である逆散乱法そのものによって与えられます。無限個の保存量が存在することは、無限自由度の系については可積分系であることの必要条件にすぎません。なぜならば、無限個ある保存量の個数と無限の自由度の数は互いに比べることができないからです。しかし、KdV方程式は実際に可積分なのであり、無限個の保存量の存在を実際に確認することで、そのことをより深く理解することはできるでしょう。説明が長くなりましたが、以下では実際に保存量を構成してみようと思います。

ここで、自明な保存量とは、$u$およびその導関数の多項式の積分で表される保存量のうち、$\int dx\,\partial_x f(u, u_x, u_{xx}, \dots)$のように微分を用いて表される量のことで、そうでない保存量のことを非自明な保存量と呼びます。

おわりに

ここまでお読み頂きありがとうございました。私の力不足で説明しきれなかった重要なトピックも数多くありますが、ソリトンおよび古典可積分系の奥深さに少しでも触れて頂けたなら嬉しいです。ではまた。