競技数学解説

文献あり

九点円の基礎と応用

初等幾何,九点円

2813

かえでです．
私が知る限りの九点円の特徴をまとめます．点,線,円の定義が省かれている場合は以前の定義に則ってください．
また，意味が分からない単語があったら各自調べてください．

初投稿 :2024/04/24
更新 : 　

九点円とは

九点円

三角形 $A B C$ において，その垂心を $H$ とし， $A, B, C$ から対辺に下ろした垂線の足をそれぞれ $D, E, F$ とし， $B C, C A, A B, A H, B H, C H$ の中点をそれぞれ $M_{A}, M_{B}, M_{C}, N_{A}, N_{B}, N_{C}$ とする．このとき， $D, E, F, M_{A}, M_{B}, M_{C}, N_{A}, N_{B}, N_{C}$ は共円である．これらの $9$ 点が通る円を三角形 $A B C$ の九点円という．

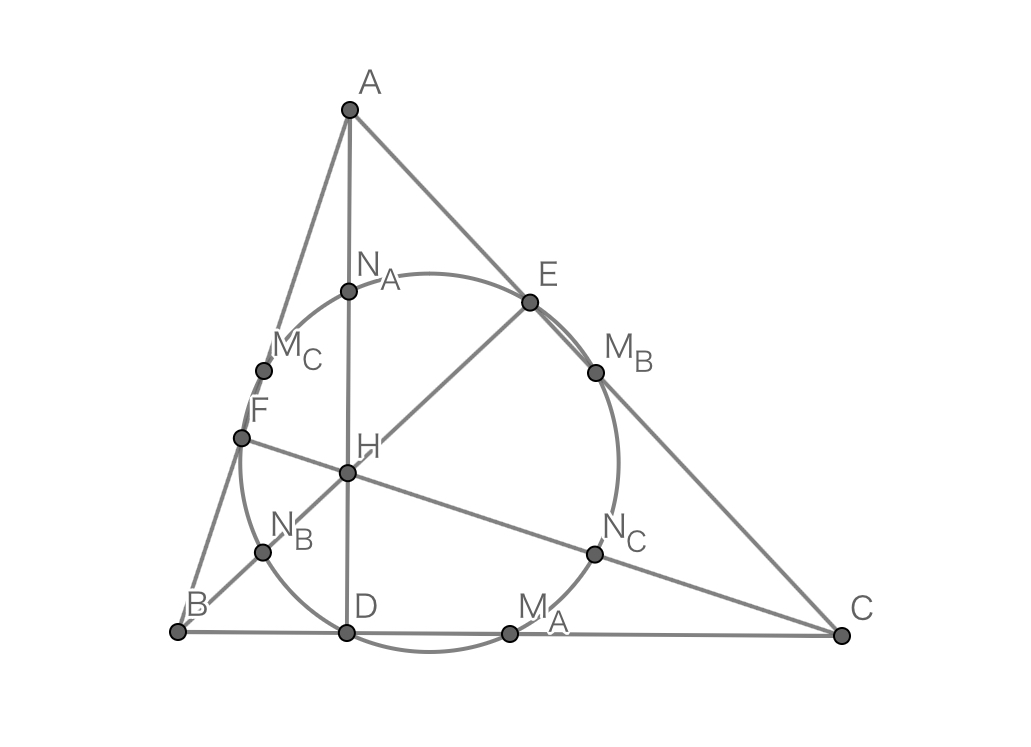九点円

以下，証明部分においては三角形 $A B C$ が鋭角三角形であるとする．鈍角三角形の場合も同様に証明ができるため各々試してみよ．

共円の証明

以降の内容に大きく通ずるような証明を与える．
相似拡大を考えることにより， $D, E, F, M_{A}, M_{B}, M_{C}$ について $H$ と対称な点が $A B C$ の外接円 $Γ$ 上にあることを示せばよい．
対称性から $D, M_{A}$ の場合のみ考えればよい．
$D, M_{A}$ について $H$ と対称な点をそれぞれ $H_{A}, A^{'}$ とする．また， $Γ$ の中心を $O$ とする．
$∠ B H_{A} C = ∠ B H C = ∠ A + 180^{\circ} - 2 ∠ A = 180^{\circ} - ∠ A$
よって， $H_{A}$ は直線 $B C$ について $A$ と反対側にあるので $A, B, C, H_{A}$ の共円が示される．
$A^{'}$ の場合の証明は読者に委ねる．
(ヒント:外心 $O$ と中点連結定理を考えてみよ)
よって，以上から九点円の存在及び九点円が外接円に垂心を中心として $1 / 2$ 倍の相似拡大を施したものであることが示された．
!FORMULA[28][488228917][0]を!FORMULA[29][36864][0]中心で!FORMULA[30][-1989117985][0]倍拡大する $Γ$ を $H$ 中心で $\frac{1}{2}$ 倍拡大する

確認問題

三角形 $A B C$ の九点円を $Ω$ とし， $Ω$ の中心を $N$ とする．このとき， $N$ が $H O$ の中点であることを示せ．
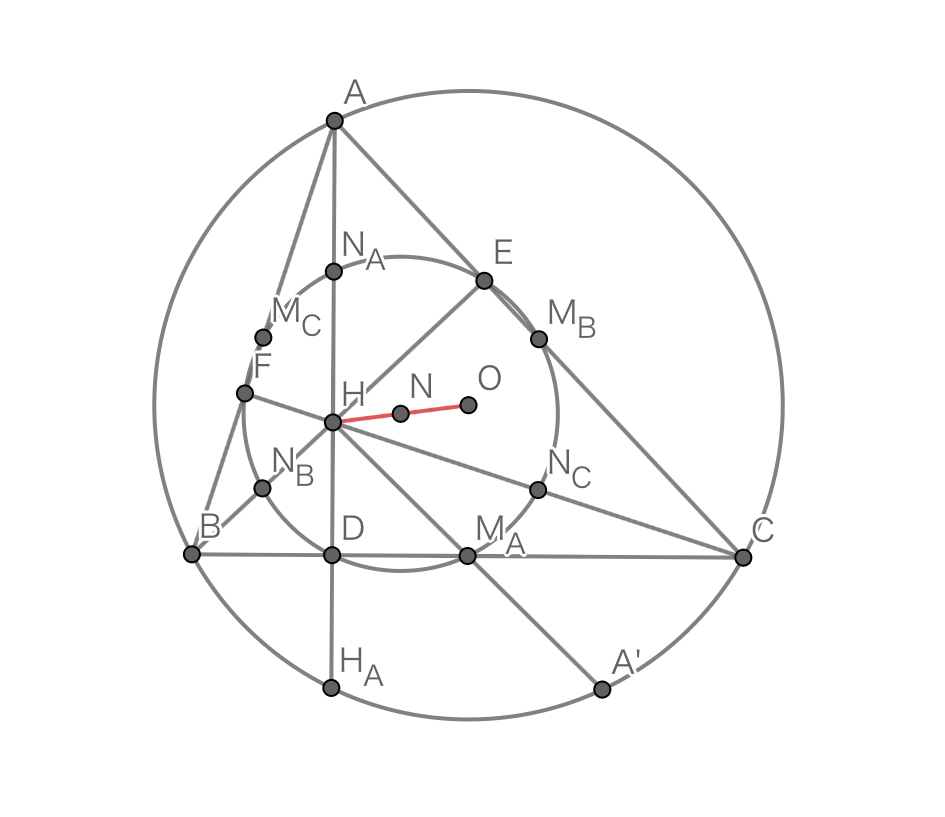問題1の図

練習問題　OMC158(F)

外接円を $Ω$ ，垂心を $H$ とする鋭角三角形 $A B C$ において， $A$ から $B C$ におろした垂線の足を $D$ ， $A C$ の中点を $M$ とし，半直線 $M D$ と $Ω$ の交点を $X$ とするとき， $A H = X H$ が成立した． $A C = 24, X D = 6$ のとき， $A B$ の長さの $2$ 乗を求めよ．
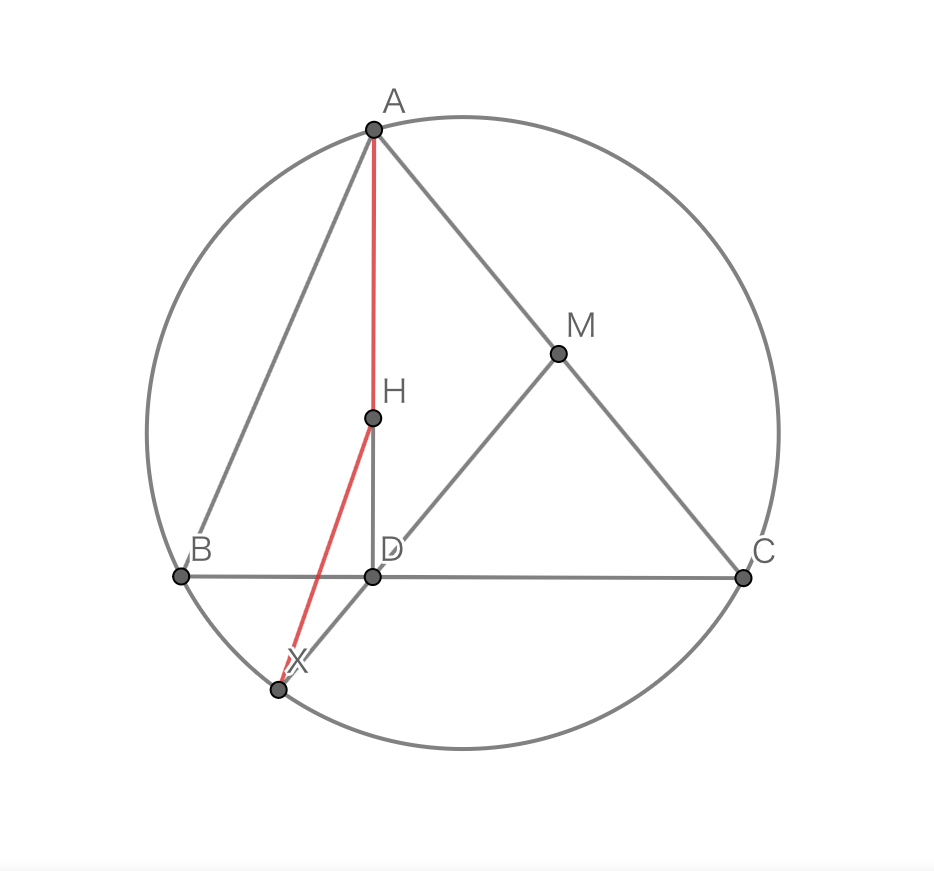問題2の図

ヒント　

九点円は方べきと相性が良いことがある．

大ヒント　

以下の図を分析してみよ．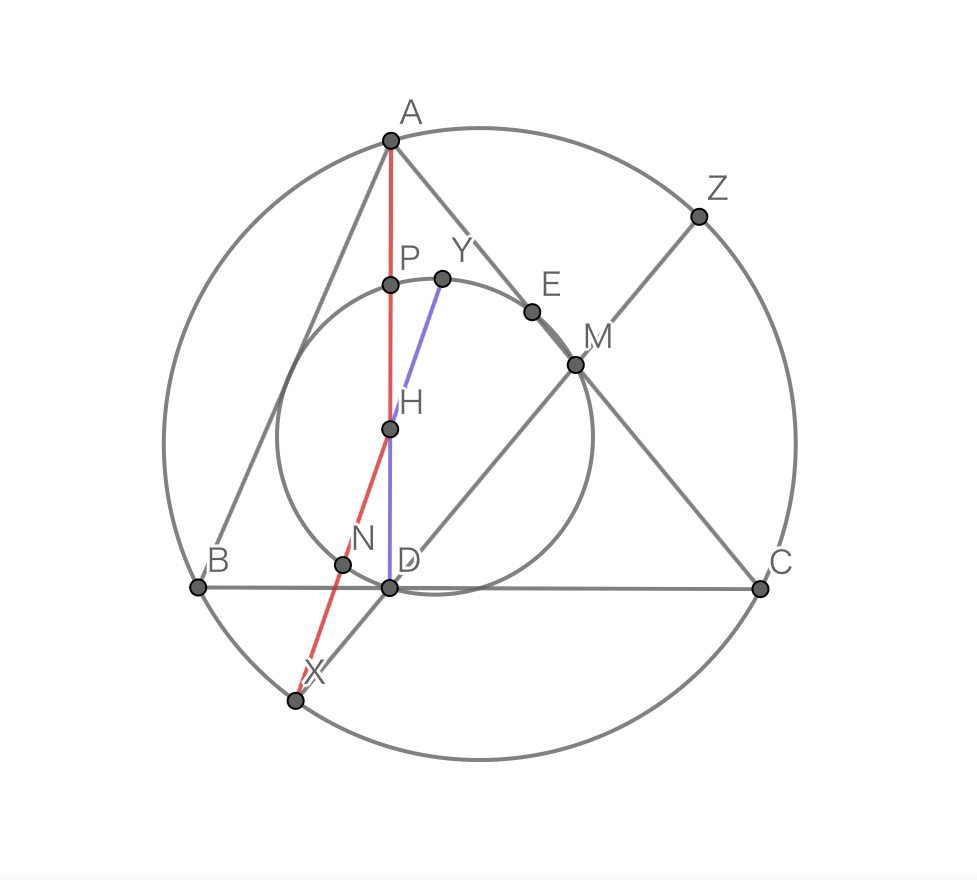

問題2の本質部分

オイラーの不等式

三角形の外接円の半径を $R$ ,内接円の半径を $r$ とする．このとき，この三角形の九点円の半径は $\frac{R}{2}$ である．
また，明らかに $\frac{R}{2} \geq r$ であるから， $R \geq 2 r$ が成り立つ．これをオイラーの不等式という．
(ただし，等号成立は三角形が正三角形のとき．)

確認問題

なぜ九点円の半径は $\frac{R}{2}$ なのか，簡潔な説明を与えよ．

ヒント　

相似拡大とはどういった概念であるか？

垂軸

まず，以下に重要な基本性質を記述する．

根軸

異なる $2$ 円に対し $2$ 円への方べきの値が等しい点の集合を根軸という．
また，根軸は必ず直線である．
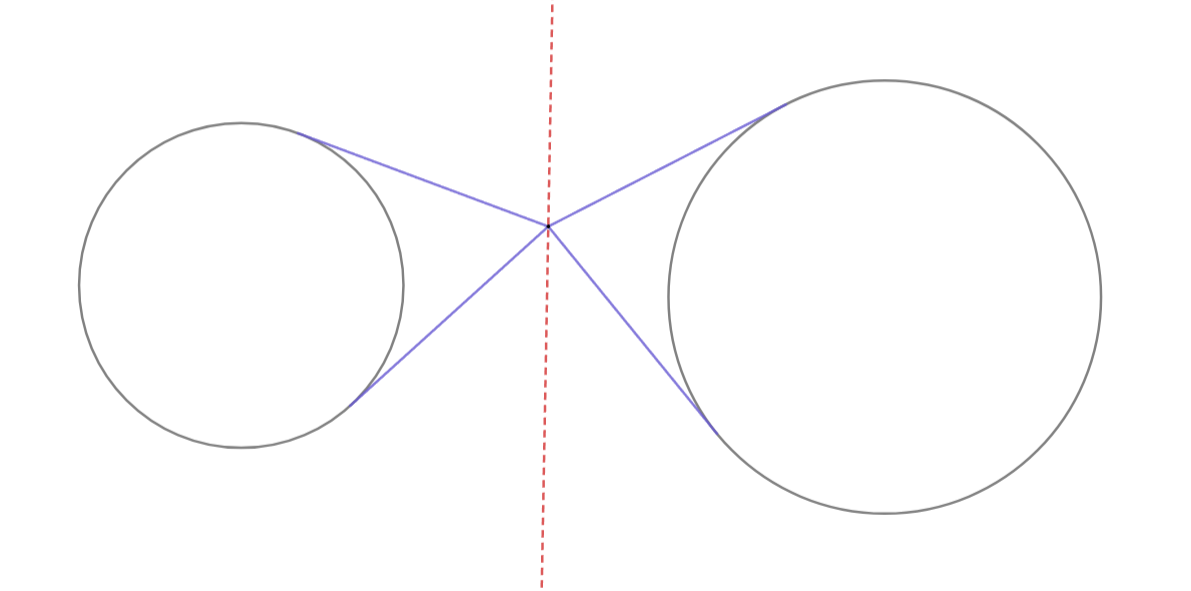赤線:根軸

異なる $2$ 円について， $2$ 円の中心を結ぶ直線と $2$ 円の根軸は直交する．

証明は読者に委ねる．
以上は必ず覚えておくべき性質である．
さて，この節の本題に入ろう．

垂軸

三角形 $A B C$ において，直線 $B C$ と直線 $E F$ の交点を $X$ とし，同様に $C A, A B$ についてそれぞれ点 $Y, Z$ を定める．
このとき， $3$ 点 $X, Y, Z$ は共線である．
この直線を三角形 $A B C$ の垂軸という．
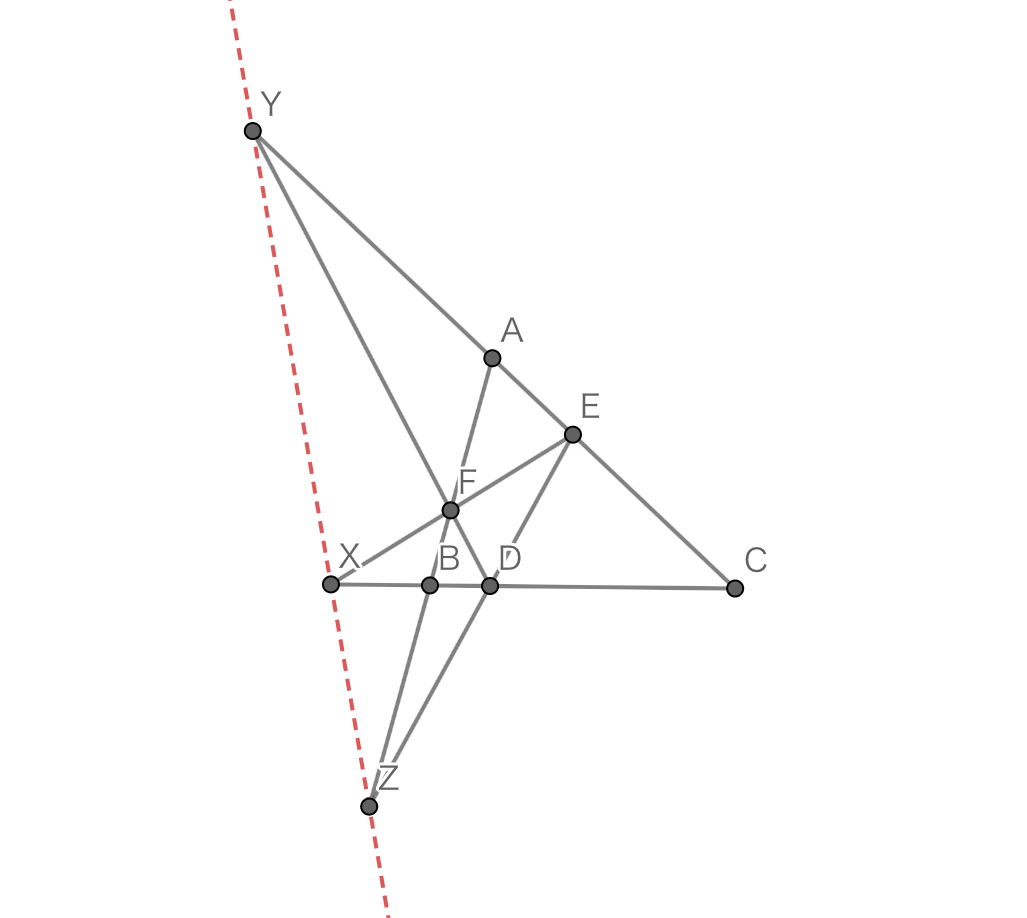赤線:垂軸

共線の証明

三角形 $A B C$ の外接円 $Γ$ と九点円 $Ω$ の根軸を $Δ$ とする．このとき，
$X B \times X C = X F \times X E$ ( $∵$ $B C E F$ の共円)
よって， $X$ は $Δ$ 上の点である．
同様に $Y, Z$ も $Δ$ 上の点である．
よって $3$ 点 $X, Y, Z$ の共線が従う．
(Desarguesの定理を用いるとより簡潔に示せる．)

垂軸とオイラー線は直交する．

これは私が初等幾何に惹かれる要因となった性質である．以下に証明を載せるがぜひ自力で証明を与えてほしい．
※オイラー線の定義は各自調べること

証明　

垂軸は

Δ

であるから定理2より直線

O N

に直交する．問題1よりこれはオイラー線である．

練習問題 (自作)

内心と外心をそれぞれ， $I, O$ とする不等辺三角形 $A B C$ において， $∠ A$ 内の傍心を $I_{A}$ とし同様に点 $I_{B}, I_{C}$ を定める．直線 $A C$ と $I_{C} B$ の交点を $X$ ，直線 $C B$ と $I_{B} A$ の交点を $Y$ ，直線 $B A$ と $I_{A} C$ の交点を $Z$ とする． $∠ A I O = 90^{\circ}$ のとき， $X Y = Z Y$ を示せ．

ヒント　

この節で得た知識をフルに活用せよ．

演習①

かえで杯　p1

鋭角三角形 $A B C$ において，その外接円を $Γ$ ，九点円を $ω$ ，外心を $O$ ， $A$ から $B C$ に下ろした垂線の足を $D$ ， $A B, A C$ の中点をそれぞれ $M, N$ とする．また， $Γ$ の $A$ における接線と $ω$ の $D$ における接線の交点を $S$ ，三角形 $S A O$ の外接円と $Γ$ の交点を $T$ とする．このとき，三角形 $A D T$ の外接円と $M N$ は $∠ A$ の二等分線上で交わることを示せ．

ヒント　

九点円を外接円に移す相似拡大の中心は垂心である．

大ヒント　

等長が見えるだろうか？

三角形 $A B C$ において， $A, B, C$ から対辺に下した垂線の足をそれぞれ $D, E, F$ とする．このとき，三角形 $A E F, B F D, C D E$ のオイラー線は三角形 $A B C$ の九点円 $Ω$ 上で交わることを示せ．

(重要)

外接円が $Γ$ である三角形 $A B C$ において， $A B, A C$ 及び円 $Γ$ に接する円はただ一つ存在するのでそれを $A -$ 混線内接円と言い，これを $Ω_{A}$ とする． $Γ$ と $Ω_{A}$ の接点を $T$ とし，三角形 $A B C$ の内心を $I$ ， $A, B, C$ に対する傍心をそれぞれ $I_{A}, I_{B}, I_{C}$ とする．このとき， $T$ について $I$ と対称な点 $T_{I}$ は円 $I_{A} I_{B} I_{C}$ 上にあることを示せ．

金木犀氏の作問

!FORMULA[146][38352][0]を求めよ $x$ を求めよ

金木犀氏の作問

!FORMULA[147][38352][0](青の面積)を求めよ $x$ (青の面積)を求めよ

シムソン線

三角形 $A B C$ において，その外接円を $Γ$ とする． $Γ$ 上に点 $P (\neq A, B, C)$ をとり， $P$ から直線 $B C, C A, A B$ に下ろした垂線の足をそれぞれ $D, E, F$ とすると， $P$ によらず $3$ 点 $D, E, F$ は共線である．この直線を三角形 $A B C$ の $P$ におけるシムソン線という．

容易なAngle chaseにより示される(複数の共円に注意)

定理4において， $P$ におけるシムソン線に対し， $P$ を中心として2倍の相似拡大を施した直線を三角形 $A B C$ の $P$ におけるシュタイナー線という．

$P$ におけるシムソン線は垂心 $H$ と $P$ の中点を通る．特に，この点は九点円上にある．

証明は少し難しいが，九点円に直接影響するような議論はしないので省く．以降要望があれば載せようと思う．

以下には非常に複雑な定理が並ぶが，以降の証明で用いることがあるので知っておいた方がよいだろう．

シュタイナー線は垂心を通る．

定理5において， $P$ を中心とする2倍の相似拡大を施せばよい．

$Γ$ 上に直径 $P Q$ を取る．このとき $P, Q$ におけるシムソン線は九点円上で直交する．

$H P, H Q$ の中点をそれぞれ $X, Y$ とする．定理5よりこれらは九点円上にあることに留意せよ．九点円を外接円に移す相似拡大を考えることにより， $X Y$ は九点円の直径を成すことが分かるので示される．

これらを数オリの問題で使うことは殆ど無いであろうが，より深くシムソン線について知りたい場合は以下のdenta氏の記事を見てみるとよい．(この記事の内容より遥かに難解である)

シムソン線であそぼう！(denta_geometry) 　　　　

フォイエルバッハの定理

以下に示す定理は初等幾何学でもっとも興味深いもののひとつである．

フォイエルバッハの定理

三角形 $A B C$ において，その九点円を $Ω$ ，内接円を $ω$ ， $A, B, C$ に対する傍接円をそれぞれ $ω_{A}, ω_{B}, ω_{C}$ とする．このとき， $Ω$ は $ω$ に内接し， $ω_{A}, ω_{B}, ω_{C}$ に外接する． $Ω$ と $ω$ の接点を，三角形 $A B C$ のフォイエルバッハ点という．

フォイエルバッハの定理を証明するにあたって，より強い主張を以下に示す．

三角形 $A B C$ において，互いに等角共役な点 $P, P^{'}$ と外心が共線ならば， $P$ の垂足円は三角形 $A B C$ の九点円に接する．

等角共役，垂足円の定義は各自調べよ．
$P$ を内心，傍心にすることでフォイエルバッハの定理が従う．

$Γ$ の中心を $O$ , $Γ$ の直径 $P P^{'}$ の両端を $X, Y$ ， $X, Y$ から $B C$ に下ろした垂線の足をそれぞれ $X^{'}, Y^{'}$ ， $P, P^{'}$ から $B C$ に下ろした垂線の足をそれぞれ $D, D^{'}$ ， $B C$ の中点を $M$ ， $Γ$ の半径を $R$ とすると，
$M D : M X^{'} = O P : R$
$M D^{'} : M X^{'} = O P^{'} : R$
よって， $(M D \times M D^{'}) : M X^{' 2} = (O P \times O P^{'}) : R^{2}$
$X, Y$ におけるシムソン線は九点円上で交わるから，この点を $L$ とすると，定理6より $L$ は $X^{'} Y^{'}$ を直径とする円上にある．よって $M X^{'} = M L$ であるから， $(M D \times M D^{'}) : M L^{2} = (O P \times O P^{'}) : R^{2}$
全く同様に， $C A, A B$ の中点をそれぞれ $N, K$ ， $P$ から $C A, A B$ へ下ろした垂線の足をそれぞれ $E, F$ ， $P^{'}$ から $C A, A B$ へ下ろした垂線の足をそれぞれ $E^{'}, F^{'}$ とすると，
$(M D \times M D^{'}) : M L^{2} = (N E \times N E^{'}) : N L^{2} = (K F \times K F^{'}) : K L^{2} = (O P \times O P^{'}) : R^{2}$
2円に関するべきの比が等しい点の軌跡は2円と共軸な定円であるから，これは九点円が $P$ の垂足円,点円 $L$ と共軸であることを示している． $L$ は九点円上の点であるから，この共軸円足の根軸は $L$ における九点円の接線である．よって $P$ での垂足円と九点円は点 $L$ で接する．

定理8によってフォイエルバッハの定理を系として証明できた．

確認問題

金木犀氏の作問

!FORMULA[229][38352][0]を求めよ $x$ を求めよ

匿氏の作問

!FORMULA[230][14236809][0]を示せ $p + y = q + x$ を示せ

演習問題 (難)

フォイエルバッハの定理 (2回目)

ここまでに得た九点円の知識を利用して，定理8を用いずにフォイエルバッハの定理の証明を与えよ．

(フォイエルバッハの定理には非常に多くの証明法が存在している．)

USA TSTST 2011/4

鋭角三角形 $A B C$ が円 $ω$ に内接しており，その垂心を $H$ ，外心を $O$ とする． $A B, A C$ の中点をそれぞれ $M, N$ とし，半直線 $M H, N H$ と $ω$ の交点をそれぞれ $P, Q$ とする．直線 $M N$ と直線 $P Q$ の交点を $R$ とするとき， $O A ⊥ R A$ を示せ．

ヒント　

いつもの相似拡大と根軸を利用せよ．

ヒント　

問題2でのヒントは見ただろうか？

USAMO 2015/2

四角形 $A P B Q$ が円 $ω$ に内接しており， $∠ P = ∠ Q = 90^{\circ}$ および $A P = A Q < B P$ をみたしている． $P Q$ 上に点 $X$ を任意にとり，直線 $A X$ と $ω$ の交点のうち $A$ でない方を $S$ とする． $ω$ の弧 $A Q B$ 上の点 $X$ は $A X ⊥ X T$ をみたし，弦 $S, T$ の中点を $M$ とする． $X$ が線分 $P Q$ 上を任意に動くとき， $M$ はある円上を動くことを示せ．

ヒント　

三角形

A S T

に注目せよ．そして，これまで通りのことをする限りである．

最後に

いかがだったでしょうか？これからも問題,定理の追加と修正は繰り返し行っていくので，是非定期的にご覧下さい！
また，初投稿時点(23/04/24)時点の予定として，次は反転のことを入れたいと思っています．
反転,射影,ミケル点などについては高度な内容なので上手くまとまってから追加していきます．
　
訂正や追加して欲しい問題などについては私のdmで教えてくださるようお願いします．
以上です．