放物線上をはね続けるボールの研究①フィボナッチ数が生えた話
はじめに
(タイトル画像 使用ツール Copilot Powered by DALL-E3)
($2024.2.25$追記)
$2024$ 年 $2$ 月 $25$ 日に開催された日曜数学会でこの記事について発表しました。
発表に使ったスライドはこちら
発表スライドへのリンク
はじまりは、Twitter(現X) での @aoki_taichi さんのこのポストでした。
曲線y=-x² に対して、(-1,0)の位置からある初速で質点を水平投射する。
— Taichi AOKI (@aoki_taichi) January 9, 2024
初速が速すぎると質点は第4象限に、遅すぎると第3象限に落ちていくが、ちょうどいい速さだと質点は曲線上を永久に跳ね続ける。https://t.co/T9cu0gW4RN pic.twitter.com/49YBAF5OK1
動画はXから引用
実際に試してみると、位置合わせがとてつもなく厳しく、ほんのわずかでもズレるととたんに奈落の底へおちていってしまいます。
@aoki_taichi さんの作品を参考に、私もDesmosで「放物線の上ではね続けさせるゲーム」を作ってみましたので、実際に触ってみてそのシビアさを体験していただければと思います。
放物線の上で質点を跳ね続けさせようゲームの図。
— ａｐｕ (@apu_yokai) February 3, 2024
手作業で位置合わせしようとしても、わずかなズレですぐに奈落に落ちてしまいます。
衝突回数を手作業で何回まで増やせるかチャレンジ！
なおチート機能（初期座標と初期速度の微調整ボタン）を実装したので、どうしても高得点が取りたい人はどうぞ😎 https://t.co/NzaBHV9Bkf pic.twitter.com/VQ3a2vp3Pc
@aoki_taichi さんによれば、重力加速度が下向きに $1$ のとき、質点が永久にはね続けるための初速は数値計算上はちょうど $\sqrt{2}$ になるらしい、というのです。
「これは面白い」と直感した私は本当に初速が $\sqrt{2}$ のときに質点が永久にはね続けるのかどうか解析してみようと思ったのでした。
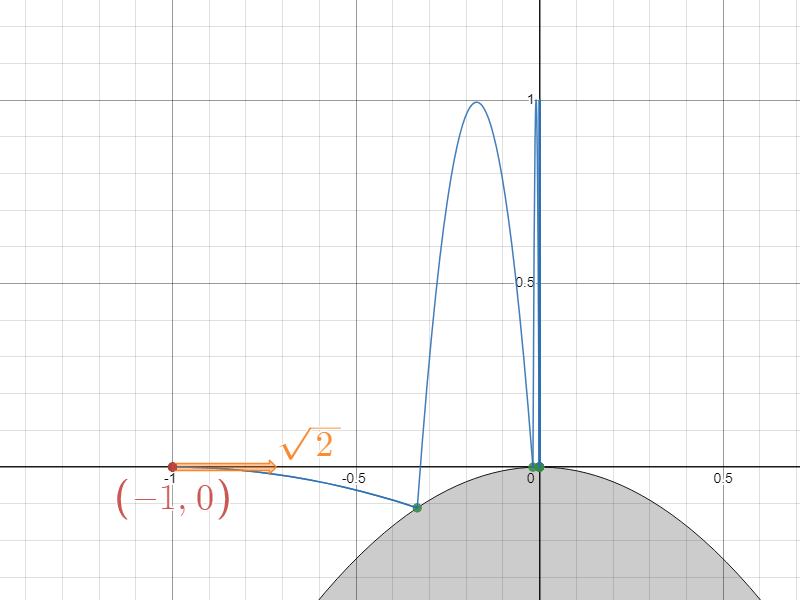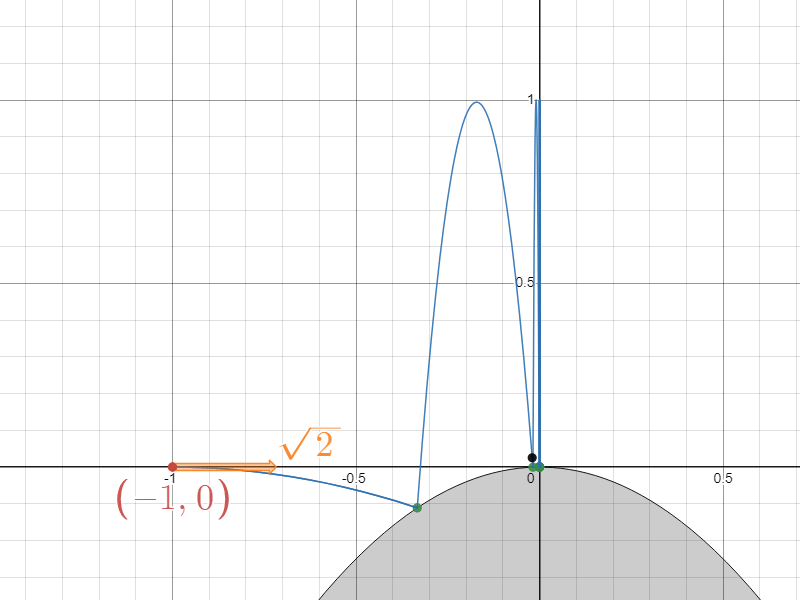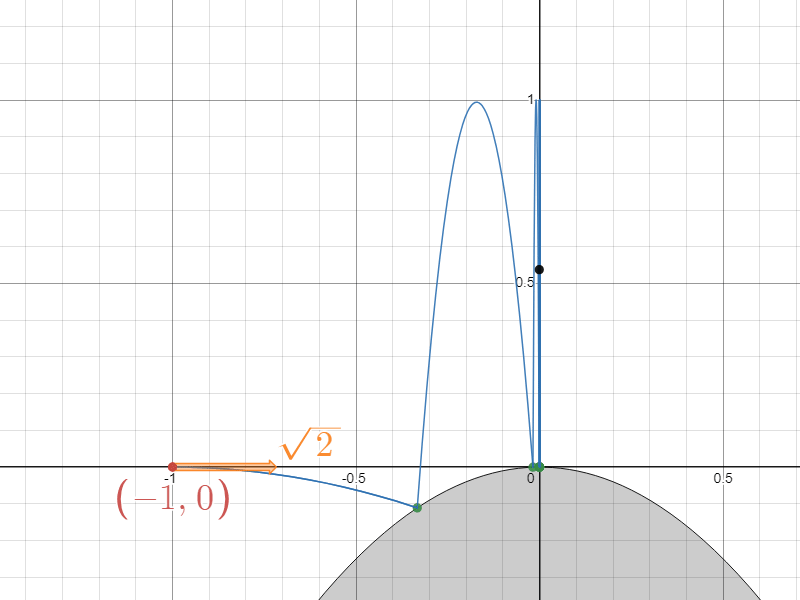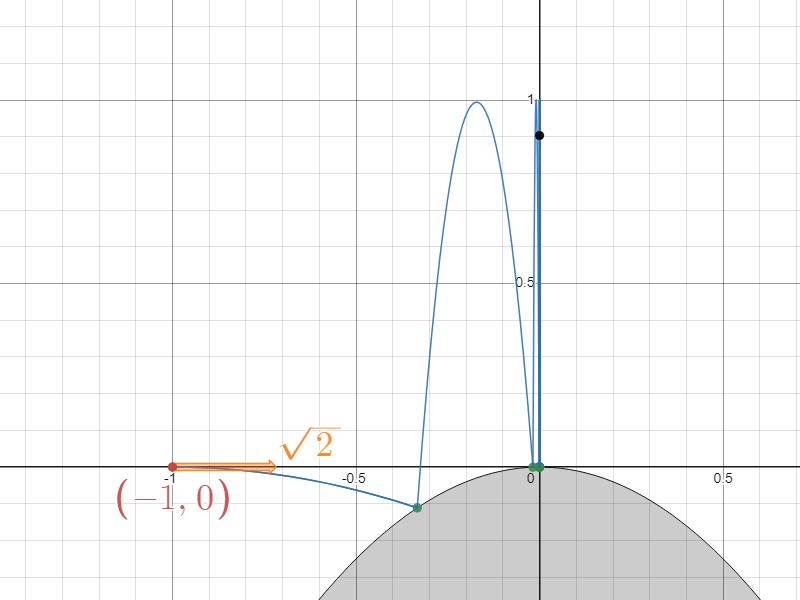永久にはね続ける
結論から言うと、この予想は正しかったのです!
しかし、それだけでは終わりませんでした。
なんと、放物線と衝突する座標などのパラメータから、フィボナッチ数が次々と現れることがわかったのです!!
この記事では、この驚くべき事実を数式で証明していきます。
なお、記事中では直感的に理解しやすいように、$x$ 軸正方向を「右向き」、$y$ 軸負方向を「下向き」などと表現しています。
観察
座標平面上に重力加速度が一様に下向きに大きさ $1$ でかかっているものとします。衝突は完全弾性衝突(反発係数$=1$)とし、空気抵抗等は考慮しないものとします。座標 $(-1,0)$ から右向きに速さ $\sqrt{2}$ で発射した質点が放物線 $C:y=-x^2$ と $n$ 回目に衝突するときの座標を $(x_n,-x_n^2)$ とし、衝突直前の速度ベクトルを $\vec{u_n}$ と、衝突直後の速度ベクトルを $\vec{v_n}$ と表し、それぞれの成分を次のように表すことにします。
${\displaystyle \vec{u_n}=\pmatrix{u_{xn}\\u_{yn}}}$
${\displaystyle \vec{v_n}=\pmatrix{v_{xn}\\v_{yn}}}$
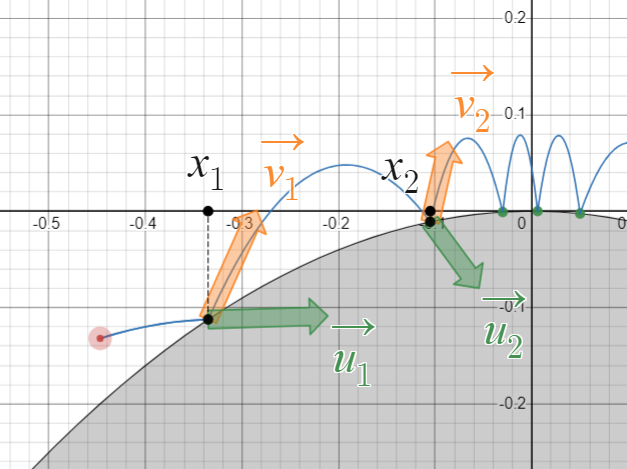記号の説明用(初期座標・初期速度は異なる)
$1$ 回目の衝突の位置・速度を計算する
発射から $1$ 回目の衝突までの質点の座標は時間を $t$ として媒介変数表示すると
$\left(-1+\sqrt{2}t,-\frac{1}{2}t^2\right)$
$t$ を消去して軌跡を求めると
$y=-\frac{1}{4}(x+1)^2$
この式と $y=-x^2$ を連立させて交点の $x$ 座標を求めると
$x=-\frac{1}{3},1$
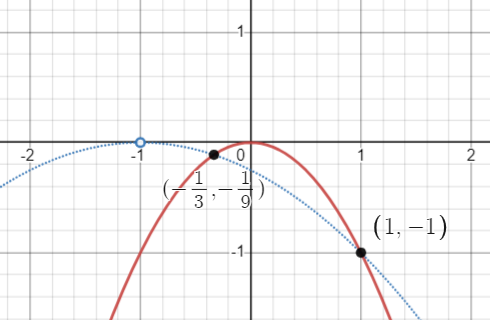軌跡と交点
$x=1$ は不適なので
$x_1=-\dfrac{1}{3}$
とわかります。衝突のときの $t$ は
$-1+\sqrt{2}t=-\frac{1}{3}$
を解いて $t=\frac{\sqrt{2}}{3}$ とわかり、ここから
${\displaystyle \vec{u_1}=\pmatrix{\sqrt{2}\\-\frac{\sqrt{2}}{3}}}$
が得られます。
次に、反射後の速度 $\vec{v_1}$ を求めます。
$\vec{A}$ の直線 $y=ax$ に対する反転 $\vec{B}$ を線形代数のパワーで計算すると
${\displaystyle \vec{B}=\frac{1}{a^2+1}\pmatrix{-a^2+1 & 2a \\ 2a & a^2-1}\vec{A} }$
証明を見るにはここをクリック
$\theta$ を $\tan\theta = a$ を満たす実数とする。
「時計周り $\theta$ 回転」「上下反転」「反時計回り $\theta$ 回転」の合成を行列式で表すと
${\displaystyle \begin{align} &\pmatrix{\cos\theta & -\sin\theta \\ \sin\theta & \cos\theta} \pmatrix{1 & 0 \\ 0 & -1} \pmatrix{\cos(-\theta) & -\sin(-\theta) \\ \sin(-\theta) & \cos(-\theta)}\\ &=\pmatrix{\cos^2\theta-\sin^2\theta & 2\cos\theta\sin\theta \\ 2\cos\theta\sin\theta & \sin^2\theta-\cos^2\theta}\\ &=\cos^2\theta\pmatrix{-\tan^2\theta+1 & 2\tan\theta \\ 2\tan\theta & \tan^2\theta-1}\\ &=\frac{1}{\tan^2\theta+1}\pmatrix{-\tan^2\theta+1 & 2\tan\theta \\ 2\tan\theta & \tan^2\theta-1}\\ &=\frac{1}{a^2+1}\pmatrix{-a^2+1 & 2a \\ 2a & a^2-1} \end{align} }$
となりますので、衝突地点での $C$ の接線の傾きが $\frac{2}{3}$ であることから
${\displaystyle \begin{align} \vec{v_1}&=\frac{1}{\left(\frac{2}{3}\right)^2+1}\pmatrix{-\left(\frac{2}{3}\right)^2+1 & \frac{4}{3} \\ \frac{4}{3} & \left(\frac{2}{3}\right)^2-1}\pmatrix{\sqrt{2}\\-\frac{\sqrt{2}}{3}}\\ &=\pmatrix{\frac{\sqrt{2}}{13}\\ \frac{41\sqrt{2}}{39}} \end{align} }$
となります。
$1$ 回目の衝突時の各パラメータ
$x_1=-\dfrac{1}{3},\vec{u_1}=\pmatrix{\sqrt{2}\\-\frac{\sqrt{2}}{3}},\vec{v_1}=\pmatrix{\frac{\sqrt{2}}{13}\\ \frac{41\sqrt{2}}{39}} $
$2$ 回目以後の衝突の位置・速度を計算する
$2$ 回目以後の衝突の位置・速度も、$1$ 回目のときと同じ方法を繰り返して計算することができるのですが、いちいち連立方程式をたてたりするのは面倒なので漸化式を作っておきましょう。
$x_n$ についての漸化式
$n$ 回目の衝突後の質点の座標を時間を $t$ として媒介変数表示すると
${\displaystyle\left(x_{n}+v_{xn}t,-x_n^2+v_{yn}t-\frac{1}{2}t^2\right)}$
$t$ を消去して軌跡を求めると
${\displaystyle y=-x_n^2+v_{yn}\cdot\frac{x-x_n}{v_{xn}}-\frac{1}{2}\left(\frac{x-x_n}{v_{xn}}\right)^2}$
この式と $y=-x^2$ を連立させて整理すると
${\displaystyle (x-x_n)\left((1-2v_{xn}^2)x-(x_n+2x_nv_{xn}^2+2v_{xn}v_{yn})\right)=0}$
これを解いて
${\displaystyle x=x_n,\frac{x_n+2x_nv_{xn}^2+2v_{xn}v_{yn}}{1-2v_{xn}^2}}$
${\displaystyle \therefore x_{n+1}=\frac{x_n+2x_nv_{xn}^2+2v_{xn}v_{yn}}{1-2v_{xn}^2}}$
${\displaystyle x_{n+1}=\frac{x_n+2x_nv_{xn}^2+2v_{xn}v_{yn}}{1-2v_{xn}^2}}$
$u_{xn},u_{yn}$ についての漸化式
$x_{n},x_{n+1},v_{xn},v_{yn}$ を使って$u_{x(n+1)},u_{y(n+1)}$ の漸化式を作ります。
${\displaystyle u_{x(n+1)}=v_{xn}}$
${\displaystyle u_{y(n+1)}=v_{yn}-\frac{x_{n+1}-x_{n}}{v_{xn}}}$
$v_{xn},v_{yn}$ についての漸化式
$C$ の $x$ 座標が $x_{n+1}$ のときの接線の傾きは $-2x_{n+1}$ ですから
${\displaystyle \pmatrix{v_{x(n+1)}\\v_{y(n+1)}}=\frac{1}{4x_{n+1}^2+1}\pmatrix{-4x_{n+1}^2+1 & -4x_{n+1} \\ -4x_{n+1} & 4x_{n+1}^2-1}\pmatrix{u_{x(n+1)}\\u_{y(n+1)}} }$
${\displaystyle v_{x(n+1)}=\frac{(-4x_{n+1}^2+1)u_{x(n+1)}-4x_{n+1}u_{y(n+1)}}{4x_{n+1}^2+1}}$
${\displaystyle v_{y(n+1)}=\frac{-4x_{n+1}u_{x(n+1)}+(4x_{n+1}^2-1)u_{y(n+1)}}{4x_{n+1}^2+1}}$
漸化式をまとめるとこうなります。
${\displaystyle x_{n+1}=\frac{x_n+2x_nv_{xn}^2+2v_{xn}v_{yn}}{1-2v_{xn}^2}}$
${\displaystyle u_{x(n+1)}=v_{xn}}$
${\displaystyle u_{y(n+1)}=v_{yn}-\frac{x_{n+1}-x_{n}}{v_{xn}}}$
${\displaystyle v_{x(n+1)}=\frac{(-4x_{n+1}^2+1)u_{x(n+1)}-4x_{n+1}u_{y(n+1)}}{4x_{n+1}^2+1}}$
${\displaystyle v_{y(n+1)}=\frac{-4x_{n+1}u_{x(n+1)}+(4x_{n+1}^2-1)u_{y(n+1)}}{4x_{n+1}^2+1}}$
得られた漸化式を使って、$n=1,2,3$ のときの $x_n,u_{xn},u_{yn},v_{xn},v_{yn}$ の値を計算すると次のようになります。
| $n$ | $x_n$ | $u_{xn}$ | $u_{yn}$ | $v_{xn}$ | $v_{yn}$ |
|---|---|---|---|---|---|
| $1$ | $-\frac{1}{3}$ | $\sqrt{2}$ | $-\frac{\sqrt{2}}{3}$ | $\frac{\sqrt{2}}{13}$ | $\frac{41\sqrt{2}}{39}$ |
| $2$ | $-\frac{1}{55}$ | $\frac{\sqrt{2}}{13}$ | $-\frac{713\sqrt{2}}{715}$ | $\frac{\sqrt{2}}{233}$ | $\frac{12817\sqrt{2}}{12815}$ |
| $3$ | $-\frac{1}{987}$ | $\frac{\sqrt{2}}{233}$ | $-\frac{229969\sqrt{2}}{229971}$ | $\frac{\sqrt{2}}{4181}$ | $\frac{4126649\sqrt{2}}{4126647}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
予想
突然ですが、ここでみんな大好きフィボナッチ数列を書き出しておきます。
・ フィボナッチ数列
$\textcolor{red}{1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,\cdots}$
先ほど得られた式を観察してみると、$x_n,u_{vn},v_{xn}$ の分母 $(\textcolor{red}{3,13,55,233,987,4181})$ がいずれもフィボナッチ数になっていることに気が付きますね。
$u_{yn},v_{yn}$ については分子も分母もフィボナッチ数ではないですが、$\sqrt{2}$ の係数の分子と分母の差がすべて $2$ になっていて法則がありそうです。分子と分母の間の数を書き出すと
$2,40,714,12816,229970,4126648$
となります。じっと見つめていると、フィボナッチ数の積で書けそうなことに気が付きますね!実際、
$2=\textcolor{red}{1\cdot2}$
$40=\textcolor{red}{5\cdot8}$
$714=\textcolor{red}{21\cdot34}$
$12816=\textcolor{red}{89\cdot144}$
$229970=\textcolor{red}{377\cdot610}$
$4126648=\textcolor{red}{1597\cdot2584}$
となり、確かにフィボナッチ数の積になっています。
これを踏まえて先ほどの表を書きなおすと
| $n$ | $x_n$ | $u_{xn}$ | $u_{yn}$ | $v_{xn}$ | $v_{yn}$ |
|---|---|---|---|---|---|
| $1$ | $-\frac{1}{\textcolor{red}{3}}$ | $\sqrt{2}$ | $-\frac{\textcolor{red}{1}\cdot\textcolor{red}{2}-1}{\textcolor{red}{1}\cdot\textcolor{red}{2}+1}\sqrt{2}$ | $\frac{\sqrt{2}}{\textcolor{red}{13}}$ | $\frac{\textcolor{red}{5}\cdot\textcolor{red}{8}+1}{\textcolor{red}{5}\cdot\textcolor{red}{8}-1}\sqrt{2}$ |
| $2$ | $-\frac{1}{\textcolor{red}{55}}$ | $\frac{\sqrt{2}}{\textcolor{red}{13}}$ | $-\frac{\textcolor{red}{21}\cdot\textcolor{red}{34}-1}{\textcolor{red}{21}\cdot\textcolor{red}{34}+1}\sqrt{2}$ | $\frac{\sqrt{2}}{\textcolor{red}{233}}$ | $\frac{\textcolor{red}{89}\cdot\textcolor{red}{144}+1}{\textcolor{red}{89}\cdot\textcolor{red}{144}-1}\sqrt{2}$ |
| $3$ | $-\frac{1}{\textcolor{red}{987}}$ | $\frac{\sqrt{2}}{\textcolor{red}{233}}$ | $-\frac{\textcolor{red}{377}\cdot\textcolor{red}{610}-1}{\textcolor{red}{377}\cdot\textcolor{red}{610}+1}\sqrt{2}$ | $\frac{\sqrt{2}}{\textcolor{red}{4181}}$ | $\frac{\textcolor{red}{1597}\cdot\textcolor{red}{2584}+1}{\textcolor{red}{1597}\cdot\textcolor{red}{2584}-1}\sqrt{2}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
赤字の数字を小さい順に並べると
$\textcolor{red}{1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181},\cdots$
なんと、フィボナッチ数列に出てくる数字が全部出てきました!!
これは私にとって、とても予想外でした。
この結果から、一般項はつぎのようにかけるのではないかと予想できますね。
| $n$ | $x_n$ | $u_{xn}$ | $u_{yn}$ | $v_{xn}$ | $v_{yn}$ |
|---|---|---|---|---|---|
| $n$ | $-\frac{1}{\textcolor{red}{F_{6n-2}}}$ | $\frac{\sqrt{2}}{\textcolor{red}{F_{6n-5}}}$ | $-\frac{\textcolor{red}{F_{6n-4}F_{6n-3}}-1}{\textcolor{red}{F_{6n-4}F_{6n-3}}+1}\sqrt{2}$ | $\frac{\sqrt{2}}{\textcolor{red}{F_{6n+1}}}$ | $\frac{\textcolor{red}{F_{6n-1}F_{6n}}+1}{\textcolor{red}{F_{6n-1}F_{6n}}-1}\sqrt{2}$ |
証明
では、この式が本当に一般の $n\in\mathbb{N}$ に対しても成り立つことを証明しましょう。
$n=1,2,3$ のときに成り立つことは先ほどの表からわかっていますので、あとは、これらの式が漸化式を満たすことさえ示せば数学的帰納法により一般の $n$ に対しても成り立つことがいえますね。
次のように漸化式に名前を付けて、順に成り立つことを確認していきましょう。
【漸化式$1$】${\displaystyle x_{n+1}=\frac{x_n+2x_nv_{xn}^2+2v_{xn}v_{yn}}{1-2v_{xn}^2}}$
【漸化式$2$】${\displaystyle u_{x(n+1)}=v_{xn}}$
【漸化式$3$】${\displaystyle u_{y(n+1)}=v_{yn}-\frac{x_{n+1}-x_{n}}{v_{xn}}}$
【漸化式$4$】${\displaystyle v_{x(n+1)}=\frac{(-4x_{n+1}^2+1)u_{x(n+1)}-4x_{n+1}u_{y(n+1)}}{4x_{n+1}^2+1}}$
【漸化式$5$】${\displaystyle v_{y(n+1)}=\frac{-4x_{n+1}u_{x(n+1)}+(4x_{n+1}^2-1)u_{y(n+1)}}{4x_{n+1}^2+1}}$
補題たち
ここからはフィボナッチ数を含む式変形をたくさんします。
そこでよく使う式変形を補題とします。
${\displaystyle F_{n+1}^2-F_{n}^2=F_{n+2}F_{n-1}}$
証明を見るにはここをクリック
${\displaystyle \begin{align} F_{n+1}^2-F_{n}^2&=\left(F_{n+1}+F_{n}\right)\left(F_{n+1}-F_{n}\right)\\ &=F_{n+2}F_{n-1} \end{align} }$
${\displaystyle F_{n+3}^2-F_{n}^2=4F_{n+2}F_{n+1}}$
証明を見るにはここをクリック
${\displaystyle \begin{align} F_{n+3}^2-F_{n}^2&=\left(F_{n+3}+F_{n}\right)\left(F_{n+3}-F_{n}\right)\\ &=\left(\left(F_{n+2}+F_{n+1}\right)+\left(F_{n+2}-F_{n+1}\right)\right)\left(\left(F_{n+2}+F_{n+1}\right)-\left(F_{n+2}-F_{n+1}\right)\right)\\ &=2F_{n+2}\cdot2F_{n+1}\\ &=4F_{n+2}F_{n+1} \end{align} }$
${\displaystyle F_{n}^2-(-1)^{n-r}F_{r}^2=F_{n+r}F_{n-r}}$
証明を見るにはここをクリック
${\displaystyle \begin{align} F_{n}^2-(-1)^{n-r}F_{r}^2&=\left(\frac{\varphi^{n}-(-\varphi)^{-n}}{\sqrt{5}}\right)^2-(-1)^{n-r}\left(\frac{\varphi^{r}-(-\varphi)^{-r}}{\sqrt{5}}\right)^2\\ &=\frac{\left(\varphi^{2n}-2(-1)^{n}+(-\varphi)^{-2n}\right)-(-1)^{n-r}\left(\varphi^{2r}-2(-1)^{r}+(-\varphi)^{-2r}\right)}{5}\\ &=\frac{\varphi^{2n}+(-\varphi)^{-2n}-(-1)^{n-r}\varphi^{2r}-(-1)^{n-r}(-\varphi)^{-2r}}{5}\\ &=\frac{\varphi^{n+r}-(-1)^{n+r}\varphi^{-(n+r)}}{\sqrt{5}}\cdot\frac{\varphi^{n-r}-(-1)^{n-r}\varphi^{-(n-r)}}{\sqrt{5}}\\ &=\frac{\varphi^{n+r}-(-\varphi)^{-(n+r)}}{\sqrt{5}}\cdot\frac{\varphi^{n-r}-(-\varphi)^{-(n-r)}}{\sqrt{5}}\\ &=F_{n+r}F_{n-r} \end{align} }$
${\displaystyle F_{n-1}F_{n+2}+(-1)^{n-1}=F_{n}F_{n+1}}$
証明を見るにはここをクリック
${\displaystyle \begin{align} F_{n-1}F_{n+2}+(-1)^{n-1}&=\frac{\varphi^{n-1}-(-\varphi)^{-n+1}}{\sqrt{5}}\cdot\frac{\varphi^{n+2}-(-\varphi)^{-n-2}}{\sqrt{5}}+(-1)^{n-1}\\ &=\frac{\varphi^{2n+1}-(-1)^{n-1}(-\varphi)^{-3}-(-1)^{n-1}\varphi^{3}+(-\varphi)^{-2n-1}}{5}+(-1)^{n-1}\\ &=\frac{\varphi^{2n+1}-(-1)^{n-1}\left(\varphi^{3}+(-\varphi)^{-3}-5\right)+(-\varphi)^{-2n-1}}{5}\\ &=\frac{\varphi^{2n+1}+(-1)^{n-1}+(-\varphi)^{-2n-1}}{5}\\ &=\frac{\varphi^{2n+1}-(-1)^{n}\left(\varphi+(-\varphi^{-1}))\right)+(-\varphi)^{-2n-1}}{5}\\ &=\frac{\varphi^{n}-(-\varphi)^{-n}}{\sqrt{5}}\cdot\frac{\varphi^{n+1}-(-\varphi)^{-n-1}}{\sqrt{5}}\\ &=F_{n}F_{n+1} \end{align} }$
${\displaystyle F_{n+6}-F_{n}=4F_{n+3}}$
証明を見るにはここをクリック
${\displaystyle \begin{align} F_{n+6}-F_{n}&=(F_{n+5}+F_{n+4})-(F_{n+2}-F_{n+1})\\ &=F_{n+5}+(F_{n+4}-F_{n+2})+F_{n+1}\\ &=(F_{n+4}+F_{n+3})+F_{n+3}+(F_{n+3}-F_{n+2})\\ &=(F_{n+4}-F_{n+2})+3F_{n+3}\\ &=4F_{n+3} \end{align} }$
漸化式 $1$ について
漸化式 $1$ に予想の式を代入すると
${\displaystyle -\frac{1}{F_{6n+4}}=\frac{-\frac{1}{F_{6n-2}}-\frac{2}{F_{6n-2}}\cdot\frac{2}{F_{6n+1}^2}+\frac{4\left(F_{6n-1}F_{6n}+1\right)}{F_{6n+1}\left(F_{6n-1}F_{6n}-1\right)}}{1-\frac{4}{F_{6n+1}^2}}}$
右辺の分母分子に $F_{6n+1}^2$ を乗じます。
${\displaystyle \Leftrightarrow -\frac{1}{F_{6n+4}}=\frac{-\frac{F_{6n+1}^2}{F_{6n-2}}-\frac{4}{F_{6n-2}}+\frac{4F_{6n+1}\left(F_{6n-1}F_{6n}+1\right)}{\textcolor{red}{F_{6n-1}F_{6n}-1}}}{\textcolor{blue}{F_{6n+1}^2-4}}}$
補題 $4$ 、補題 $3$ を使います。
${\displaystyle \Leftrightarrow -\frac{1}{F_{6n+4}}=\frac{-\frac{F_{6n+1}^2}{F_{6n-2}}-\frac{4}{F_{6n-2}}+\frac{4\textcolor{#00BBAA}{F_{6n+1}}\left(F_{6n-1}F_{6n}+1\right)}{\textcolor{#00BBAA}{F_{6n+1}}F_{6n-2}}}{F_{6n+4}F_{6n-2}}}$
${\displaystyle \Leftrightarrow -\frac{1}{F_{6n+4}}=\frac{-\frac{F_{6n+1}^2}{F_{6n-2}}-\frac{4}{F_{6n-2}}+\frac{4\left(F_{6n-1}F_{6n}+1\right)}{F_{6n-2}}}{F_{6n+4}F_{6n-2}}}$
両辺に $F_{6n-2}^2 F_{6n+4}$ を乗じます。
${\displaystyle \Leftrightarrow -F_{6n-2}^2=-F_{6n+1}^2-4+4\left(F_{6n-1}F_{6n}+1\right)}$
${\displaystyle \Leftrightarrow -\left(F_{6n+1}^2-F_{6n-2}^2\right)+4F_{6n-1}F_{6n}=0}$
補題 $2$ を使います。
${\displaystyle \Leftrightarrow -4F_{6n}F_{6n-1}+4F_{6n-1}F_{6n}=0}$
予想の式が漸化式 $1$ を満たすことが確認できました!
漸化式 $2$ について
漸化式 $2$ に予想の式を代入すると
${\displaystyle \frac{\sqrt{2}}{F_{6(n+1)-5}}=\frac{\sqrt{2}}{F_{6n+1}}}$
予想の式が漸化式 $2$ を満たすことは明らかですね。
漸化式 $3$ について
漸化式 $3$ に予想の式を代入すると
${\displaystyle -\frac{F_{6n+2}F_{6n+3}-1}{F_{6n+2}F_{6n+3}+1}\sqrt{2}=\frac{F_{6n-1}F_{6n}+1}{F_{6n-1}F_{6n}-1}\sqrt{2}-\frac{-\frac{1}{F_{6n+4}}+\frac{1}{F_{6n-2}}}{\frac{\sqrt{2}}{F_{6n+1}}}}$
${\displaystyle \Leftrightarrow -\frac{F_{6n+2}F_{6n+3}-1}{F_{6n+2}F_{6n+3}+1}=\frac{F_{6n-1}F_{6n}+1}{F_{6n-1}F_{6n}-1}-\frac{\frac{\textcolor{red}{F_{6n+4}-F_{6n-2}}}{F_{6n+4}F_{6n-2}}}{\frac{2}{F_{6n+1}}}}$
補題 $5$ を使います。
${\displaystyle \Leftrightarrow -\frac{F_{6n+2}F_{6n+3}-1}{F_{6n+2}F_{6n+3}+1}=\frac{F_{6n-1}F_{6n}+1}{F_{6n-1}F_{6n}-1}-\frac{\frac{4F_{6n+1}}{F_{6n+4}F_{6n-2}}}{\frac{2}{F_{6n+1}}}}$
${\displaystyle \Leftrightarrow -\frac{F_{6n+2}F_{6n+3}-1}{\textcolor{red}{F_{6n+2}F_{6n+3}+1}}=\frac{F_{6n-1}F_{6n}+1}{\textcolor{blue}{F_{6n-1}F_{6n}-1}}-\frac{2F_{6n+1}^2}{F_{6n+4}F_{6n-2}}}$
補題 $4$ を使います。
${\displaystyle \Leftrightarrow -\frac{F_{6n+2}F_{6n+3}-1}{F_{6n+1}F_{6n+4}}=\frac{F_{6n-1}F_{6n}+1}{F_{6n-2}F_{6n+1}}-\frac{2F_{6n+1}^2}{F_{6n+4}F_{6n-2}}}$
両辺に $F_{6n-2}F_{6n+1}F_{6n+4}$ を乗じます。
${\displaystyle \Leftrightarrow -F_{6n-2}F_{6n+2}F_{6n+3}+F_{6n-2}=F_{6n+4}F_{6n-1}F_{6n}+F_{6n+4}-2F_{6n+1}^3}$
${\displaystyle \Leftrightarrow F_{6n-2}F_{6n+2}F_{6n+3}+F_{6n+4}F_{6n-1}F_{6n}-2F_{6n+1}^3+(F_{6n+4}-F_{6n-2})=0}$
うまい変形を思いつかなかったので、一旦フィボナッチ数を全て $F_{6n},F_{6n+1}$ を使った式に書き換えてゴリ押すことにします。
${\displaystyle \Leftrightarrow (2F_{6n}-F_{6n+1})(F_{6n+1}+F_{6n})(2F_{6n+1}+F_{6n})+(3F_{6n+1}+2F_{6n})(F_{6n+1}-F_{6n})F_{6n}-2F_{6n+1}^3+4F_{6n+1}=0}$
${\displaystyle \Leftrightarrow 4F_{6n+1}\left(F_{6n}^2+F_{6n}F_{6n+1}-F_{6n+1}^2+1\right)=0}$
${\displaystyle \Leftrightarrow F_{6n}^2+F_{6n}F_{6n+1}-F_{6n+1}^2+1=0}$
${\displaystyle \Leftrightarrow -(\textcolor{red}{F_{6n+1}^2-F_{6n}^2})+(\textcolor{blue}{F_{6n}F_{6n+1}+1})=0}$
補題 $1$、補題 $4$ を使います。
${\displaystyle \Leftrightarrow -F_{6n+2}F_{6n-1}+F_{6n-1}F_{6n+2}=0}$
予想の式が漸化式 $3$ を満たすことが確認できました!
漸化式 $4$ について
漸化式 $4$ に予想の式を代入すると
${\displaystyle \frac{\sqrt{2}}{F_{6n+7}}=\frac{\left(-\frac{4}{F_{6n+4}^2}+1\right)\frac{\sqrt{2}}{F_{6n+1}}-\frac{4}{F_{6n+4}}\frac{F_{6n+2}F_{6n+3}-1}{F_{6n+2}F_{6n+3}+1}\sqrt{2}}{\frac{4}{F_{6n+4}^2}+1}}$
右辺の分母分子に $F_{6n+4}^2$ を乗じます。
${\displaystyle \Leftrightarrow \frac{\sqrt{2}}{F_{6n+7}}=\frac{\left(-4+F_{6n+4}^2\right)\frac{\sqrt{2}}{F_{6n+1}}-\frac{4F_{6n+4}(F_{6n+2}F_{6n+3}-1)}{F_{6n+2}F_{6n+3}+1}\sqrt{2}}{4+F_{6n+4}^2}}$
${\displaystyle \Leftrightarrow \frac{1}{F_{6n+7}}=\frac{\left(-4+F_{6n+4}^2\right)\frac{1}{F_{6n+1}}-\frac{4F_{6n+4}(F_{6n+2}F_{6n+3}-1)}{\textcolor{red}{F_{6n+2}F_{6n+3}+1}}}{\textcolor{blue}{4+F_{6n+4}^2}}}$
補題 $3$ を使います。
${\displaystyle \Leftrightarrow \frac{1}{F_{6n+7}}=\frac{\left(-4+F_{6n+4}^2\right)\frac{1}{F_{6n+1}}-\frac{4\textcolor{#00BBAA}{F_{6n+4}}(F_{6n+2}F_{6n+3}-1)}{F_{6n+1}\textcolor{#00BBAA}{F_{6n+4}}}}{F_{6n+7}F_{6n+1}}}$
両辺に $F_{6n+1}^2F_{6n+7}$ を乗じます。
${\displaystyle \Leftrightarrow F_{6n+1}^2=\left(-4+F_{6n+4}^2\right)-4(F_{6n+2}F_{6n+3}-1)}$
${\displaystyle \Leftrightarrow \left(\textcolor{red}{F_{6n+4}^2-F_{6n+1}^2}\right)-4F_{6n+2}F_{6n+3}=0}$
補題 $2$ を使います。
${\displaystyle \Leftrightarrow 4F_{6n+3}F_{6n+2}-4F_{6n+2}F_{6n+3}=0}$
予想の式が漸化式 $4$ を満たすことが確認できました!
漸化式 $5$ について
漸化式 $5$ に予想の式を代入すると
${\displaystyle\frac{F_{6n+5}F_{6n+6}+1}{F_{6n+5}F_{6n+6}-1}\sqrt{2}=\frac{\frac{4}{F_{6n+4}}\cdot\frac{\sqrt{2}}{F_{6n+1}}-\left(\frac{4}{F_{6n+4}^2}-1\right)\cdot \frac{F_{6n+2}F_{6n+3}-1}{F_{6n+2}F_{6n+3}+1}\sqrt{2}}{\frac{4}{F_{6n+4}^2}+1}}$
${\displaystyle \Leftrightarrow \frac{F_{6n+5}F_{6n+6}+1}{F_{6n+5}F_{6n+6}-1}=\frac{\frac{4F_{6n+4}}{F_{6n+1}}-\left(4-F_{6n+4}^2\right)\cdot \frac{F_{6n+2}F_{6n+3}-1}{F_{6n+2}F_{6n+3}+1}}{4+F_{6n+4}^2}}$
${\displaystyle \Leftrightarrow 1+\frac{2}{F_{6n+5}F_{6n+6}-1}=\frac{\frac{4F_{6n+4}}{F_{6n+1}}-\left(4-F_{6n+4}^2\right)\left(1-\frac{2}{F_{6n+2}F_{6n+3}+1}\right)}{4+F_{6n+4}^2}}$
${\displaystyle \Leftrightarrow 1+\frac{2}{\textcolor{#00BBAA}{F_{6n+5}F_{6n+6}-1}}=\frac{\frac{4F_{6n+4}}{F_{6n+1}}-\left(4-F_{6n+4}^2\right)\left(1-\frac{2}{\textcolor{red}{F_{6n+2}F_{6n+3}+1}}\right)}{\textcolor{blue}{4+F_{6n+4}^2}}}$
補題 $4$、補題 $3$ を使います。
${\displaystyle \Leftrightarrow 1+\frac{2}{\textcolor{#00BBAA}{F_{6n+4}F_{6n+7}}}=\frac{\frac{4F_{6n+4}}{F_{6n+1}}-\left(4-F_{6n+4}^2\right)\left(1-\frac{2}{\textcolor{red}{F_{6n+1}F_{6n+4}}}\right)}{\textcolor{blue}{F_{6n+1}F_{6n+7}}}}$
両辺に $F_{6n+1}^2F_{6n+4}F_{6n+7}$ を乗じます。
${\displaystyle \Leftrightarrow F_{6n+1}^2F_{6n+4}F_{6n+7}+2F_{6n+1}^2=4F_{6n+4}^2-\left(4-F_{6n+4}^2\right)\left(F_{6n+1}F_{6n+4}-2\right)}$
${\displaystyle \Leftrightarrow F_{6n+1}^2F_{6n+4}F_{6n+7}+2F_{6n+1}^2-4F_{6n+4}^2+\left(4-F_{6n+4}^2\right)\left(F_{6n+1}F_{6n+4}-2\right)=0}$
${\displaystyle \Leftrightarrow F_{6n+1}^2F_{6n+4}F_{6n+7}+2F_{6n+1}^2-4F_{6n+4}^2-F_{6n+1}F_{6n+4}^3+2F_{6n+4}^2+4F_{6n+1}F_{6n+4}-8=0}$
${\displaystyle \Leftrightarrow F_{6n+1}F_{6n+4}\cdot \textcolor{red}{F_{6n+1}F_{6n+7}}-2(\textcolor{blue}{F_{6n+4}^2-F_{6n+1}^2})-F_{6n+1}F_{6n+4}^3+4F_{6n+1}F_{6n+4}-8=0}$
補題 $3$、補題 $2$ を使います。
${\displaystyle \Leftrightarrow F_{6n+1}F_{6n+4}\left(\textcolor{red}{F_{6n+4}^2+4}\right)-2\cdot\textcolor{blue}{4F_{6n+2}F_{6n+3}}-F_{6n+1}F_{6n+4}^3+4F_{6n+1}F_{6n+4}-8=0}$
${\displaystyle \Leftrightarrow 8F_{6n+1}F_{6n+4}-8F_{6n+2}F_{6n+3}-8=0}$
${\displaystyle \Leftrightarrow \textcolor{red}{F_{6n+1}F_{6n+4}-1}- F_{6n+2}F_{6n+3}=0}$
補題 $4$ を使います。
${\displaystyle \Leftrightarrow \textcolor{red}{F_{6n+2}F_{6n+3}}- F_{6n+2}F_{6n+3}=0}$
予想の式が漸化式 $5$ を満たすことが確認できました!
これで、予想の式が全ての漸化式を満たすことが確認できましたので、数学的帰納法により、予想の式が確かに一般項となることが証明できたことになります。
| $n$ | $x_n$ | $u_{xn}$ | $u_{yn}$ | $v_{xn}$ | $v_{yn}$ |
|---|---|---|---|---|---|
| $n$ | $-\frac{1}{\textcolor{red}{F_{6n-2}}}$ | $\frac{\sqrt{2}}{\textcolor{red}{F_{6n-5}}}$ | $-\frac{\textcolor{red}{F_{6n-4}F_{6n-3}}-1}{\textcolor{red}{F_{6n-4}F_{6n-3}}+1}\sqrt{2}$ | $\frac{\sqrt{2}}{\textcolor{red}{F_{6n+1}}}$ | $\frac{\textcolor{red}{F_{6n-1}F_{6n}}+1}{\textcolor{red}{F_{6n-1}F_{6n}}-1}\sqrt{2}$ |
おわりに……おわりませんでした
一般項ができたことで $n\to\infty$ の極限も計算できるので、先ほどの表に $\infty$ も加えて書き直してこの記事をしめくくるつもりだったのですが……
| $n$ | $x_n$ | $u_{xn}$ | $u_{yn}$ | $v_{xn}$ | $v_{yn}$ |
|---|---|---|---|---|---|
| $1$ | $-\frac{1}{\textcolor{red}{3}}$ | $\sqrt{2}$ | $-\frac{\textcolor{red}{1}\cdot\textcolor{red}{2}-1}{\textcolor{red}{1}\cdot\textcolor{red}{2}+1}\sqrt{2}$ | $\frac{\sqrt{2}}{\textcolor{red}{13}}$ | $\frac{\textcolor{red}{5}\cdot\textcolor{red}{8}+1}{\textcolor{red}{5}\cdot\textcolor{red}{8}-1}\sqrt{2}$ |
| $2$ | $-\frac{1}{\textcolor{red}{55}}$ | $\frac{\sqrt{2}}{\textcolor{red}{13}}$ | $-\frac{\textcolor{red}{21}\cdot\textcolor{red}{34}-1}{\textcolor{red}{21}\cdot\textcolor{red}{34}+1}\sqrt{2}$ | $\frac{\sqrt{2}}{\textcolor{red}{233}}$ | $\frac{\textcolor{red}{89}\cdot\textcolor{red}{144}+1}{\textcolor{red}{89}\cdot\textcolor{red}{144}-1}\sqrt{2}$ |
| $3$ | $-\frac{1}{\textcolor{red}{987}}$ | $\frac{\sqrt{2}}{\textcolor{red}{233}}$ | $-\frac{\textcolor{red}{377}\cdot\textcolor{red}{610}-1}{\textcolor{red}{377}\cdot\textcolor{red}{610}+1}\sqrt{2}$ | $\frac{\sqrt{2}}{\textcolor{red}{4181}}$ | $\frac{\textcolor{red}{1597}\cdot\textcolor{red}{2584}+1}{\textcolor{red}{1597}\cdot\textcolor{red}{2584}-1}\sqrt{2}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| $\to\infty$ | $0$ | $0$ | $-\sqrt{2}$ | $0$ | $\sqrt{2}$ |
そこでふと気が付いてしまったのです。「フィボナッチ数はマイナスにも拡張できるよね?もしかして……」と。
フィボナッチ数は漸化式を $F_{n-1}=F_{n+1}-F_{n}$ と書き換えることによって、マイナス方向にも拡張できることが知られています。
${\displaystyle \begin{array}{c|ccc} n & \cdots & -6 & -5 & -4 & -3 & -2 & -1 & 0 & 1 & 2 & 3 & 4 & 5 & 6 & \cdots \\ \hline F(n) & \cdots & -8 & 5 & -3 & 2 & -1 & 1 & 0 & 1 & 1 & 2 & 3 & 5 & 8 & \cdots \\ \end{array} }$
さきほどの表もマイナスに拡張できそうに思われます。しかし、質点の進行方向を逆にしたとき、言い換えると「$(-1,0)$ から左向きに $\sqrt{2}$ の速さで打ち出した質点は放物線 $C$ に衝突することなく奈落へ落ちていく」のです。いったいどういうことでしょうか?
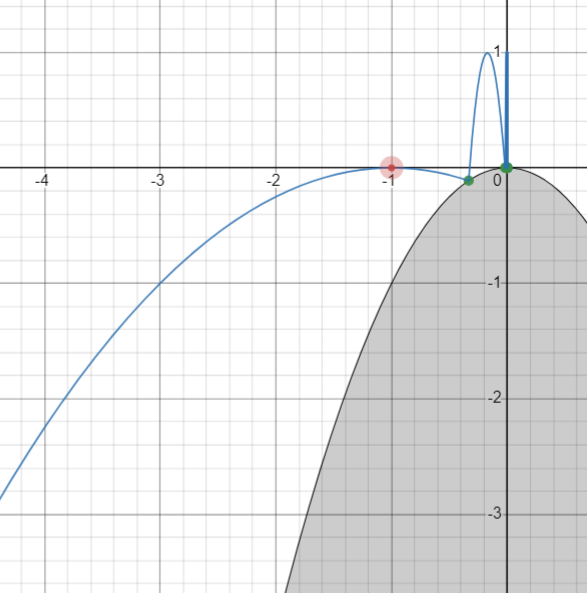左向きは衝突しない
ともかく、計算した座標と速度がどんな軌跡を描くのかグラフで確認してみましょう。すると・・・
もう一つの軌道(質点の軌道は計算結果と逆向きにしている)
なんと、無限に衝突し続ける軌道がもう一つ現れました。
具体的には、座標 $(1,-1)$ に対して入射速度 $\pmatrix{-\sqrt{2}\\ \sqrt{2}}$ で衝突する軌道が永久にはね続ける軌道になります。
正のフィボナッチ数の軌道と負のフィボナッチ数の軌道を重ねるとこうなります。
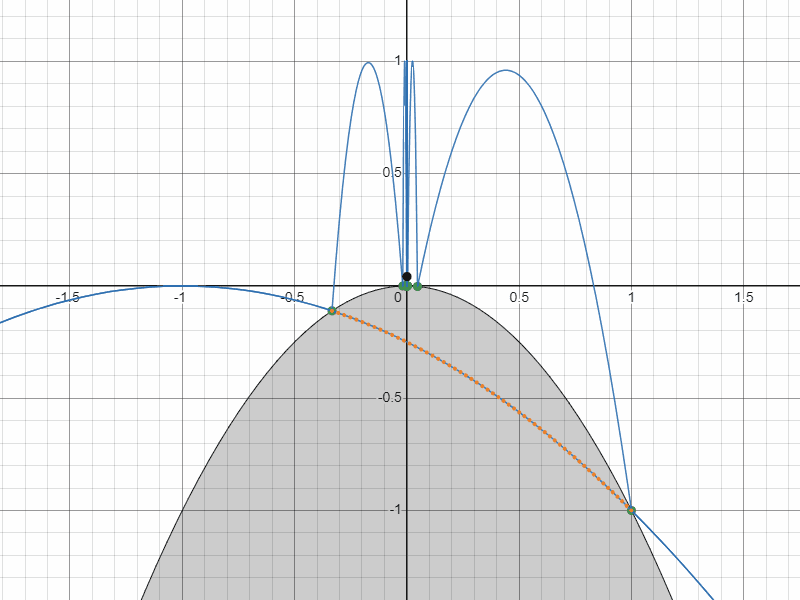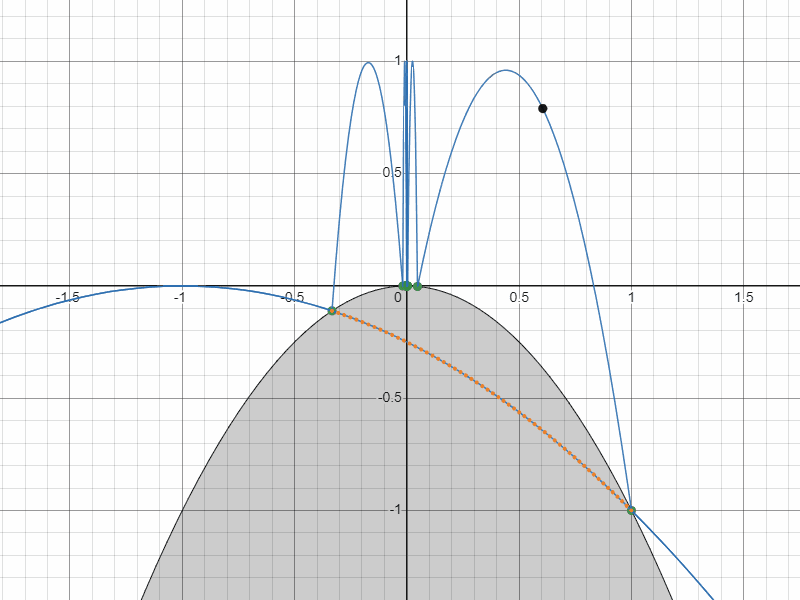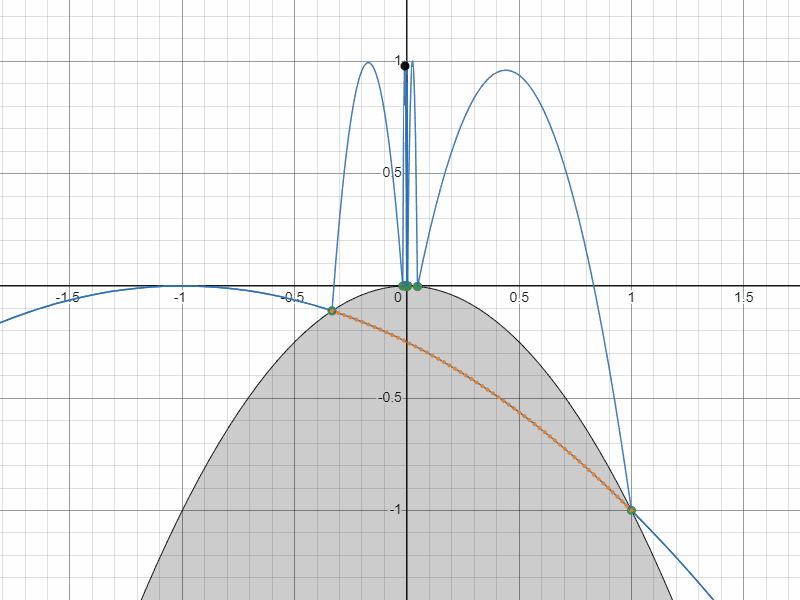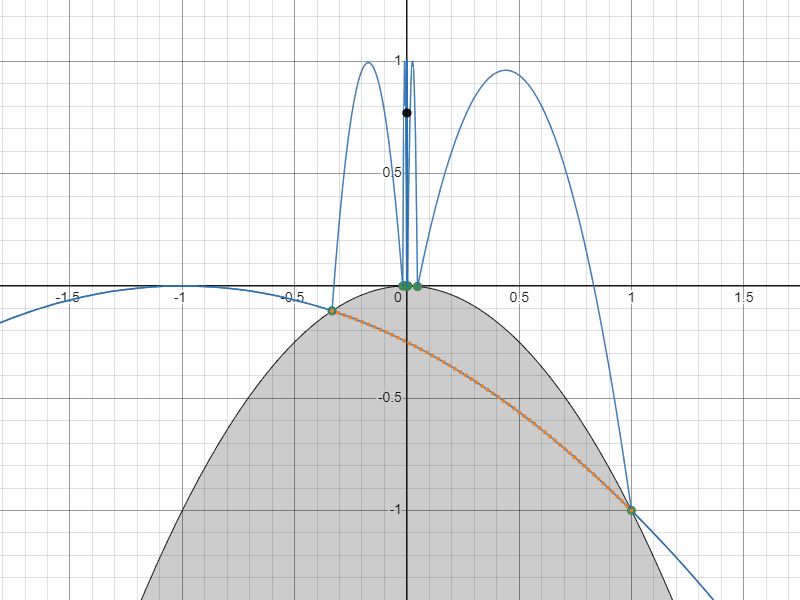負のフィボナッチ数の軌道と正のフィボナッチ数の軌道の関係
お気づきでしょうか?
負のフィボナッチ数による軌道が右下の方の奈落へ落ちて行ったあと、同じ放物線を今度は左下から這い上がってきて復活するような軌道になっていることを!
これはなんとも予想外で面白い軌道だと思います。
特に、座標と速度のパラメータとして、全てのフィボナッチ数が、つまり正のフィボナッチ数だけでなく負のフィボナッチ数を含む全てが現れるところがお気に入りです。
おわりに
最後に、先ほどの表にマイナスのフィボナッチ数も含めて書き直してこの記事を締めくくりたいと思います。
| $n$ | $x_n$ | $u_{xn}$ | $u_{yn}$ | $v_{xn}$ | $v_{yn}$ |
|---|---|---|---|---|---|
| $\to-\infty$ | $0$ | $0$ | $-\sqrt{2}$ | $0$ | $\sqrt{2}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| $-2$ | $-\frac{1}{\textcolor{red}{-377}}$ | $\frac{\sqrt{2}}{\textcolor{red}{1597}}$ | $-\frac{\textcolor{red}{(-987)}\cdot\textcolor{red}{610}-1}{\textcolor{red}{(-987)}\cdot\textcolor{red}{610}+1}\sqrt{2}$ | $\frac{\sqrt{2}}{\textcolor{red}{89}}$ | $\frac{\textcolor{red}{233}\cdot\textcolor{red}{(-144)}+1}{\textcolor{red}{233}\cdot\textcolor{red}{(-144)}-1}\sqrt{2}$ |
| $-1$ | $-\frac{1}{\textcolor{red}{-21}}$ | $\frac{\sqrt{2}}{\textcolor{red}{89}}$ | $-\frac{\textcolor{red}{(-55)}\cdot\textcolor{red}{34}-1}{\textcolor{red}{(-55)}\cdot\textcolor{red}{34}+1}\sqrt{2}$ | $\frac{\sqrt{2}}{\textcolor{red}{5}}$ | $\frac{\textcolor{red}{13}\cdot\textcolor{red}{(-8)}+1}{\textcolor{red}{13}\cdot\textcolor{red}{(-8)}-1}\sqrt{2}$ |
| $0$ | $-\frac{1}{\textcolor{red}{-1}}$ | $\frac{\sqrt{2}}{\textcolor{red}{5}}$ | $-\frac{\textcolor{red}{(-3)}\cdot\textcolor{red}{2}-1}{\textcolor{red}{(-3)}\cdot\textcolor{red}{2}+1}\sqrt{2}$ | $\frac{\sqrt{2}}{\textcolor{red}{1}}$ | $\frac{\textcolor{red}{1}\cdot\textcolor{red}{0}+1}{\textcolor{red}{1}\cdot\textcolor{red}{0}-1}\sqrt{2}$ |
| $1$ | $-\frac{1}{\textcolor{red}{3}}$ | $\frac{\sqrt{2}}{\textcolor{red}{1}}$ | $-\frac{\textcolor{red}{1}\cdot\textcolor{red}{2}-1}{\textcolor{red}{1}\cdot\textcolor{red}{2}+1}\sqrt{2}$ | $\frac{\sqrt{2}}{\textcolor{red}{13}}$ | $\frac{\textcolor{red}{5}\cdot\textcolor{red}{8}+1}{\textcolor{red}{5}\cdot\textcolor{red}{8}-1}\sqrt{2}$ |
| $2$ | $-\frac{1}{\textcolor{red}{55}}$ | $\frac{\sqrt{2}}{\textcolor{red}{13}}$ | $-\frac{\textcolor{red}{21}\cdot\textcolor{red}{34}-1}{\textcolor{red}{21}\cdot\textcolor{red}{34}+1}\sqrt{2}$ | $\frac{\sqrt{2}}{\textcolor{red}{233}}$ | $\frac{\textcolor{red}{89}\cdot\textcolor{red}{144}+1}{\textcolor{red}{89}\cdot\textcolor{red}{144}-1}\sqrt{2}$ |
| $3$ | $-\frac{1}{\textcolor{red}{987}}$ | $\frac{\sqrt{2}}{\textcolor{red}{233}}$ | $-\frac{\textcolor{red}{377}\cdot\textcolor{red}{610}-1}{\textcolor{red}{377}\cdot\textcolor{red}{610}+1}\sqrt{2}$ | $\frac{\sqrt{2}}{\textcolor{red}{4181}}$ | $\frac{\textcolor{red}{1597}\cdot\textcolor{red}{2584}+1}{\textcolor{red}{1597}\cdot\textcolor{red}{2584}-1}\sqrt{2}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| $\to+\infty$ | $0$ | $0$ | $-\sqrt{2}$ | $0$ | $\sqrt{2}$ |
| $n$ | $x_n$ | $u_{xn}$ | $u_{yn}$ | $v_{xn}$ | $v_{yn}$ |
|---|---|---|---|---|---|
| $n$ | $-\frac{1}{\textcolor{red}{F_{6n-2}}}$ | $\frac{\sqrt{2}}{\textcolor{red}{F_{6n-5}}}$ | $-\frac{\textcolor{red}{F_{6n-4}F_{6n-3}}-1}{\textcolor{red}{F_{6n-4}F_{6n-3}}+1}\sqrt{2}$ | $\frac{\sqrt{2}}{\textcolor{red}{F_{6n+1}}}$ | $\frac{\textcolor{red}{F_{6n-1}F_{6n}}+1}{\textcolor{red}{F_{6n-1}F_{6n}}-1}\sqrt{2}$ |
いやあ壮観ですね!
これでこの記事は今度こそおしまいです。
しかし、これで謎が全て解けたとは思っていません。例えば、「なぜ速さが $\sqrt{2}$ のときに永久にはね続けるのか」については何も解決できていません。
特に、フィボナッチ数との関係については、計算結果から偶然フィボナッチ数であることを発見しただけで、「なぜフィボナッチ数が現れるのか」、そこにより深い謎が隠れているような気がしてなりません。
さらに、「初期座標から無限にはね続ける初期速度を求めるような式はあるか」など、関連する疑問がどんどんわいてきます。
皆さんも是非、この問題を楽しんでいただき、何か面白い発見があれば教えていただければ幸いです。
なお、補題2のシンプルな証明方法は Twitter(現X) で
@taylor2173
さんに教えていただきました。ありがとうございました。
そして何より、ネタ元の
@aoki_taichi
さんに感謝をこめてこの記事を捧げたいと思います。
本当にありがとうこざいました!
($2024.2.17$ 追記)
・「初期座標から無限にはね続ける初期速度を求めるような式はあるか」の疑問については肯定的に解決することができました!この記事の続編となる「
【Mathlog】放物線の上をはね続けるボールの研究②はね続ける条件の話
」の記事をご覧ください。
この記事を高評価した人
この記事に送られたバッジ
投稿者
