6
高校数学解説

放物線上をはね続けるボールの研究②はね続ける条件の話

放物線,焦点,自由落下
223
1
$$$$

はじめに

　この記事は、先日公開した 【Mathlog】放物線上をはね続けるボールの研究①フィボナッチ数が生えた話 と関連のある内容となっています。
　時間のある方はこの記事と合わせてお読みいただくとよりいっそう楽しめると思います。

　この記事では前回の記事の「おわりに」で挙げた疑問「初期座標から無限にはね続ける初期速度を求めるような式はあるか」を肯定的に解決できた、という内容になります!
　つまり、放物線より上の任意の点を初期座標として、永久にはね続ける速度を構成する方法が分かったのです!
　さらには、その速度には自由度があり、任意の点から無数の軌道を造ることが可能です。
　この記事ではそのことを解説していきます。

　前提は前回の記事と同様です。すなわち、座標平面上に重力加速度が一様に下向きに大きさ 1 でかかっているものとします。衝突は完全弾性衝突(反発係数=1)とし、空気抵抗等は考慮しないものとします。初期座標と初期速度を与えられた質点が放物線 $C:y=-x^2$ に衝突して跳ね返るときの軌道を考察します。ただし、初期座標は $C$ よりも上とします。
　また、放物線 $C$ の焦点 $\left(0,-\dfrac{1}{4}\right)$ を $F$ と表します。
　なお、記事中では直感的に理解しやすいように、$x$ 軸正方向を「右向き」、$y$ 軸正方向を「上向き」などと表現しています。

(2024.3.17追記)　符号誤り等の軽微な修正をしました。

試してみよう

　百聞は一見に如かず。というわけでまずはこちらの Desmos 作品をご覧ください。

【Desmos】放物線の上で反射～AUTOモード追加

　これは前回の記事の冒頭でご紹介した作品に「AUTO」ボタンを追加したものです。
「AUTO」ボタンを押すと、初期座標と初期速度の「向き」はそのままに、初期速度の「速さ」だけを永久にはね続ける速さに自動調整してくれます。

　ただし、「ある条件」を満たしていない場合には「AUTO」ボタンは消えてしまいます。その条件は赤い点とオレンジの点、すなわち、初期座標と初期速度を表している点をつなぐ直線が、放物線 $C$ の焦点 $F$ よりも上を通っているという条件です。

はね続ける条件

　それでは、永久にはね続ける条件とはなんでしょうか。
　それはズバリ、
　「質点の軌道の延長線上に放物線 $C$ の焦点 $F$ がある」
　これだけです!
　先ほどのDesmos作品では、質点の軌道の延長線上に放物線 $C$ の焦点 $F$ が来るように速さを自動調整していたのでした。
　そして、初期座標と初期速度を表している点をつなぐ直線が、放物線 $C$ の焦点 $F$ よりも下の場合、どんなに速度を早くしても焦点を通る軌道にすることは不可能なので、「AUTO」ボタンを消すようにしていたのでした。

証明の全体の流れ

　見通しをよくするために、今からやることの全体の流れをまず説明します。
　証明は２段階で行います。

　①　衝突前の質点の軌道(延長上含む)に $F$ がある場合、衝突後の質点の軌道(延長上含む)にも $F$ がある。
　②　衝突点の $x$ 座標は 衝突を繰り返すたびに $0$ へ近づく。

②が成り立てば、衝突地点の $x$ 座標が $0$ に近づきながら永久にはね続けることがいえるというわけです。

衝突前に焦点を通る軌道は衝突後も焦点を通る軌道となる

　衝突前の質点の軌道(延長上含む)を $T_1$ 、衝突後の質点の軌道(延長上含む)を $T_2$ とします。質点が座標 $(x_n,-x_n^2)$ ではねるときを考え、はねる瞬間に速度ベクトルが ${\displaystyle{ u_{x(n)} \choose u_{y(n)}}}$ から ${\displaystyle{ v_{x(n)} \choose v_{y(n)}}}$
に変化したとします。
　なお、議論を簡単にするため、 $x_n\ne0,u_{x(n)}\ne0,v_{x(n)}\ne0$ のときだけ考えることにします。

${\displaystyle v_{x(n)}=\frac{(-4x_{n}^2+1)u_{x(n)}-4x_{n}u_{y(n)}}{4x_{n}^2+1}}$

${\displaystyle v_{y(n)}=\frac{-4x_{n}u_{x(n)}+(4x_{n}^2-1)u_{y(n)}}{4x_{n}^2+1}}$

対称性から

${\displaystyle u_{x(n)}=\frac{(-4x_{n}^2+1)v_{x(n)}-4x_{n}v_{y(n)}}{4x_{n}^2+1}}$

${\displaystyle u_{y(n)}=\frac{-4x_{n}v_{x(n)}+(4x_{n}^2-1)v_{y(n)}}{4x_{n}^2+1}}$

衝突前の質点の軌道 $T_1$ は

${\displaystyle x=x_n+u_{x(n)}t}$

${\displaystyle y=-x_n^2+u_{y(n)}t-\frac{1}{2}t^2}$

から $t$ を消去して
　${\displaystyle y=-x_n^2+u_{y(n)}\cdot\frac{x-x_n}{u_{x(n)}}-\frac{1}{2}\cdot\frac{(x-x_n)^2}{u_{x(n)}^2}}$

と書けます。

この軌道が $C$ の焦点 $F$ を通るとき

　${\displaystyle -\frac{1}{4}=-x_n^2+u_{y(n)}\cdot\frac{0-x_n}{u_{x(n)}}-\frac{1}{2}\cdot\frac{(0-x_n)^2}{u_{x(n)}^2}}$

変形して

　${\displaystyle \frac{4x_n^2-1}{4}+u_{y(n)}\cdot\frac{x_n}{u_{x(n)}}+\frac{1}{2}\cdot\frac{x_n^2}{u_{x(n)}^2}=0}$

　${\displaystyle \frac{(4x_n^2-1)u_{x(n)}+4x_nu_{y(n)}}{4u_{x(n)}}+\frac{x_n^2}{2u_{x(n)}^2}=0}$

が成り立ち、逆にこの式が成り立つとき $T_1$ は $F$ を通ります。

　$T_1$ が $F$ を通る必要十分条件

　${\displaystyle \frac{(4x_n^2-1)u_{x(n)}+4x_nu_{y(n)}}{4u_{x(n)}}+\frac{x_n^2}{2u_{x(n)}^2}=0}$

両辺に ${\displaystyle \frac{4u_{x(n)}}{2x_n^2(4x_n^2+1)}}$ を乗じて

　${\displaystyle \frac{(4x_n^2-1)u_{x(n)}+4x_nu_{y(n)}}{2x_n^2(4x_n^2+1)}+\frac{1}{u_{x(n)}(4x_n^2+1)}=0}$

この式に

　${\displaystyle v_{x(n)}=\frac{(-4x_{n}^2+1)u_{x(n)}-4x_{n}u_{y(n)}}{4x_{n}^2+1}}$

　${\displaystyle u_{x(n)}=\frac{(-4x_{n}^2+1)v_{x(n)}-4x_{n}v_{y(n)}}{4x_{n}^2+1}}$

を使って $u_{x(n)},u_{x(n)}$ を消去すると

　${\displaystyle \frac{-v_{x(n)}}{2x_n^2}+\frac{1}{(-4x_{n}^2+1)v_{x(n)}-4x_{n}v_{y(n)}}=0}$

両辺に 　${\displaystyle \frac{2x_n^2\left((-4x_{n}^2+1)v_{x(n)}-4x_{n}v_{y(n)}\right)}{4v_{x(n)}^2}}$ を乗じて

　${\displaystyle \frac{-v_{x(n)}}{2x_n^2}\cdot\frac{2x_n^2\left((-4x_{n}^2+1)v_{x(n)}-4x_{n}v_{y(n)}\right)}{4v_{x(n)}^2}+\frac{1}{(-4x_{n}^2+1)v_{x(n)}-4x_{n}v_{y(n)}}\cdot\frac{2x_n^2\left((-4x_{n}^2+1)v_{x(n)}-4x_{n}v_{y(n)}\right)}{4v_{x(n)}^2}=0}$

　${\displaystyle -\frac{\left((-4x_{n}^2+1)v_{x(n)}-4x_{n}v_{y(n)}\right)}{4v_{x(n)}}+\frac{x_n^2}{2v_{x(n)}^2}=0}$

　${\displaystyle \therefore \frac{(4x_{n}^2-1)v_{x(n)}+4x_{n}v_{y(n)}}{4v_{x(n)}}+\frac{x_n^2}{2v_{x(n)}^2}=0}$

　${\displaystyle \frac{(4x_{n}^2-1)v_{x(n)}+4x_{n}v_{y(n)}}{4v_{x(n)}}+\frac{x_n^2}{2v_{x(n)}^2}=0}$

　この形は、軌道 $T_1$ が $F$ を通る必要十分条件となる式

　${\displaystyle \frac{(4x_n^2-1)u_{x(n)}+4x_nu_{y(n)}}{4u_{x(n)}}+\frac{x_n^2}{2u_{x(n)}^2}=0}$

の $u$ を $v$ に入れ替えたものと完全に一致しています。

すなわち、軌道 $T_2$ も $C$ の焦点 $F$ を通ることがわかりました。

永久に繰り返すことの証明

　衝突前の軌道が $F$ を通る軌道であり、かつ、最初の衝突後の速度の $x$ 成分が直線 $x=0$ に近づく向きだった場合、すなわち

　$x_1<0$ ならば $v_{x(1)}>0$
　$x_1>0$ ならば $v_{x(1)}<0$

の条件を満たすときに、衝突回数が無限に発散することを示します。
　なお、対称性から、$x_1<0$ のときについてのみ考察します。

　衝突前に $F$ を通る軌道は衝突後も $F$ を通る軌道になることは既に証明しました。
　ということは、その次の衝突後の軌道も、更にその次の衝突後の軌道も $F$ を通る軌道になることになりますから、一度 $F$ を通る軌道で発射した質点は、その後何回衝突しても $F$ を通る軌道となります。

　図$1$ をご覧ください。
　$F$ を通る放物線 $T_1$を右向きに移動してきた質点が点 $A$ で $C$ に衝突し、軌道が $T_2$ に変化したとします。放物線 $C$ の $A$ における接線と $y$ 軸との交点を点 $B$ とします。$A$ と $x$ 座標が同じ点を $A$ の上にとり点 $P$ とします。線分 $FA$ の延長上に点 $Q$を、線分 $BA$ の延長上に点 $R$ をそれぞれとります。

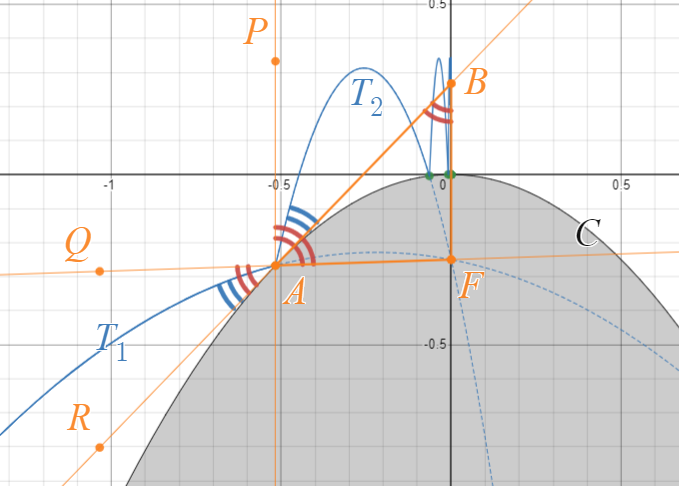
　$A$ の座標を $(x_1,-x_1^2)$ とします。放物線 $C$ の点 $A$ における接線は

　$(y+x_1^2)=-2x_1(x-x_1)$

となります。
$x=0$ を代入して $y=x_1^2$ となることから点 $B$ の座標は $(0,x_1^2)$ となります。

　$ \begin{align} |\overrightarrow{FA}|&=\sqrt{x_1^2+\left(-x_1^2+\frac{1}{4}\right)^2}\\ &=\sqrt{x_1^4+\frac{x_1^2}{2}+\frac{1}{16}}\\ &=\sqrt{\left(x_1^2+\frac{1}{4}\right)^2}\\ &=x_1^2+\frac{1}{4} \end{align}$
　${\displaystyle|\overrightarrow{FB}|=x_1^2+\frac{1}{4}}$

　$\therefore |\overrightarrow{FA}|=|\overrightarrow{FB}|$

　$\triangle FAB$ は二等辺三角形であることから $\angle FAB=\angle FBA$
　$\angle FBA$ と $\angle PAB$ は錯角なので　$\angle FBA=\angle PAB$
　$\angle FAB$ と $\angle QAR$ は対頂角なので　$\angle FAB=\angle QAR$

　したがって

　$\angle FAB=\angle FBA=\angle PAB=\angle QAR$

となります。

　$\angle FAB=\angle FBA=\angle PAB=\angle QAR$

　質点が $T_1$ 上を点 $A$ に向かうとき、$T_1$ は上に凸で $2$ 点 $A,F$ を通過する放物線ですから、点 $A$ の近傍では直線 $RA$ より上かつ直線 $QA$ よりも下を通過します。

　$\angle RAQ=\angle BAP$ ですから、質点が反射して $T_2$ 上を通過するとき、 $A$ の近傍では直線 $BA$ より上かつ直線 $PA$ より右を通過することになります。

　このことから、反射後の質点の速度の $x$ 成分の正負は、反射前と一致することがわかります。
　次に $T_2$ の軌道に注目します。
　$T_2$ の軌道は $2$ 点 $A,F$ を通る放物線です。
　$T_2$ の軌道は $A$ の近傍では $AB$ より上、すなわち $C$ の上であり、$F$ の近傍では $C$ の下となっていますから、中間値の定理により、$T_2$ と $C$ の交点で $x$ 座標が $A$ と $F$ の間にあるものが存在することがわかります。
　その交点の座標が、 $A$ で衝突した後に 質点が $C$ に衝突する座標ということになります。
　式で表すと

　$x_{1}<0 \Rightarrow x_{1}< x_{2}<0$

ということです。
　これを繰り返すことで

　$x_{1}<0 \Rightarrow x_{1}< x_{2}< x_{3}< x_{4}< x_{5}\cdots<0$

となることがわかります。
　すなわち、この軌道は無限回衝突しながら $x=0$ に近づいていく軌道、言い換えると「永久にはね続ける軌道」であることということです!

発見に至る道のり

　というわけで無事に「初期座標から無限にはね続ける初期速度を求めるような式はあるか」という疑問に対し、「質点の軌道の延長上を $F$ が通過する速度にすれば無限にはね続ける」という解答が得られました。
　また、そのような速度は各座標ごとに自由度 $1$ で無数にあることもわかりますね。
　それで、どうやってこの式を見つけたかというと、そのきっかけは　@aoki_taichi さんのこのポストでした。

　下に凸な放物線 $y=x^2$ の上から質点を発射する場合、その軌道が放物線 $y=x^2$ の焦点 $\left(0,\dfrac{1}{4}\right)$ を通過するものであれば、$x$ 座標が $0$ に収束していくというのです。数値実験でこの重要な事実を発見したとは凄いですね。
　私はこのポストを見て、「これって上に凸な放物線 $y=-x^2$ のときも同様になるのでは?」と思い、実際にシミュレーションしてみたらそのとおりになったのでした。
　また、数値実験だけでなく数式での証明の完成には、 @emiemi_ogaoga さんのこのポストに助けていただきました。

　ほかにも色々なコメントをいただき、参考にさせていただいています。
　皆さんありがとうございました。

おわりに

　というわけで永久にはね続ける初期条件を見つけることができたのですが、謎はまだまだありそうです。
　例えば、@aoki_taichi さんの数値実験から、永久にはね続ける軌道には、全ての反射軌道に接するような放物線があるのではないか、そしてその放物線の焦点も元の放物線の焦点と一致するのではないか、という予想がたちます。

　$y=-x^2$ の場合、無限にはね続ける軌道に接触する放物線の式は

このような式になるものと予想できますが、まだ証明できていません。

　それから、「$F$ を通らない軌道」についてもほとんどわかっていませんが、@aoki_taichi さんの数値実験からは何らかの法則性のようなものがあるように思えます。
　前回の記事の「終わりに」にも書いた最大の謎、「なぜフィボナッチ数が現れるのか」についても何もわかっていません。
　皆さんも是非これらのことについて考えてみて欲しいと思います。そして、何か見つけたら教えていただければ幸いです!

投稿日：2月17日
更新日：3月16日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

投稿者

apu_yokai
apu_yokai
434
50983

コメント

他の人のコメント

コメントはありません。
読み込み中
apu_yokai
apu_yokai
放物線上をはね続けるボールの研究②はね続ける条件の話