ζ(3)と余弦積分の面白い関係
2022年12月30日の夜のメッセージ
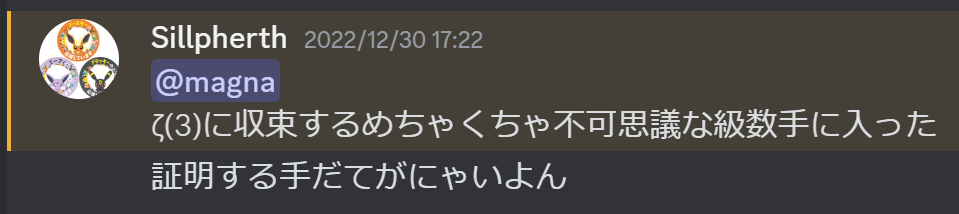
ちょうど一年前、Sillpherthがこんなメッセージを送ってきた。
 Sillpherthより。
Sillpherthより。
どうやら、$\zeta(3)$に収束する面白い級数を発見したらしい。
その主張がコチラ。
$${\zeta(3)=\sum_{m=0}^{\infty}\Big(1+4\pi^2 m^2\mathrm{Ci}(2\pi m)\Bigr)}$$
めちゃくちゃ面白いですね。これを証明して行きます。
簡単な関係式1
\begin{align} \qquad \sum_{n=-\infty}^{\infty}\frac{1}{(|n|+1)^3} &=1+2\sum_{n=1}^{\infty}\frac{1}{(n+1)^3}\\ &=-1+2\sum_{n=1}^{\infty}\frac{1}{n^3}\\ &=2\zeta(3)-1 \end{align}
ポアソン和公式[ wiki ]
\begin{align} \qquad \sum_{n=-\infty}^{\infty}\frac{1}{(|n|+1)^3} &=\sum_{m=-\infty}^{\infty}\mathcal{F}_n\left[\frac{1}{(|n|+1)^3}\right](m)&\text{ポアソン和公式}\\ &=\sum_{m=-\infty}^{\infty} \int_{-\infty}^{\infty}\frac{e^{-2\pi imx}}{(|x|+1)^3}dx\\ &=\sum_{m=-\infty}^{\infty} \int_{-\infty}^{0}\frac{e^{-2\pi imx}}{(|x|+1)^3}dx+\int_{0}^{\infty}\frac{e^{-2\pi imx}}{(|x|+1)^3}dx\\ &=\sum_{m=-\infty}^{\infty} \int_{0}^{\infty}\frac{e^{2\pi imx}}{(x+1)^3}dx+\int_{0}^{\infty}\frac{e^{-2\pi imx}}{(x+1)^3}dx\\ &=\sum_{m=-\infty}^{\infty} \int_{0}^{\infty}\frac{2\cos(2\pi mx)}{(x+1)^3}dx \end{align}
積分の計算1
\begin{align} \qquad \int_{0}^{\infty}\frac{2\cos(2\pi mx)}{(x+1)^3}\,dx &=\left[-\frac{\cos(2\pi mx)}{(x+1)^2}\right]_{0}^{\infty} -2\pi m\int_{0}^{\infty}\frac{\sin(2\pi mx)}{(x+1)^2}dx\\ &=1-2\pi m\int_{0}^{\infty}\frac{\sin(2\pi mx)}{(x+1)^2}dx\\ &=1-2\pi m \left( \left[-\frac{\sin(2\pi mx)}{x+1}\right]_{0}^{\infty} +2\pi m\int_{0}^{\infty}\frac{\cos(2\pi mx)}{x+1}dx \right)\\ &=1-4\pi^2 m^2 \int_{0}^{\infty}\frac{\cos(2\pi mx)}{x+1}dx\\ \end{align}
簡単な関係式2
加法定理より
\begin{align}
\qquad \cos(2\pi m(x-1))&=\cos(2\pi mx-2\pi m)\\[3mm]
&=\cos2\pi mx\cos2\pi m+\sin2\pi mx\sin2\pi m\\[3mm]
&=\cos2\pi mx
\end{align}
最後の変形は、$m$が整数であることを用いている。
積分の計算2
\begin{align} \qquad \int_{0}^{\infty}\frac{\cos(2\pi mx)}{x+1}dx &=\int_{1}^{\infty}\frac{\cos(2\pi m(x-1))}{x}dx\\[1mm] &=\int_{1}^{\infty}\frac{\cos(2\pi mx)}{x}dx&\text{簡単な関係式2}\\[1mm] &=\int_{2\pi m}^{\infty}\frac{\cos z}{z}dz&z\coloneqq 2\pi mx\\[2mm] &=-\mathrm{Ci}(2\pi m)&\mathrm{Ci}(x)=-\int_{x}^{\infty}\frac{\cos z}{z}dz \end{align}
まとめると...
\begin{align}
\qquad 2\zeta(3)-1&=\sum_{n=-\infty}^{\infty}\frac{1}{(|n|+1)^3}&\text{簡単な関係式1}\\[1mm]
&=\sum_{m=-\infty}^{\infty}
\int_{0}^{\infty}\frac{2\cos(2\pi mx)}{(x+1)^3}dx&\text{ポアソン和公式}\\[1mm]
&=\sum_{m=-\infty}^{\infty}
\left(1-4\pi^2 m^2
\int_{0}^{\infty}\frac{\cos(2\pi mx)}{x+1}dx \right)&\text{積分の計算1}\\[1mm]
&=\sum_{m=-\infty}^{\infty}
\Big(1+4\pi^2 m^2\mathrm{Ci}(2\pi m)\Bigr)&\text{積分の計算2}\\[1mm]
&=-1+2\sum_{m=0}^{\infty}\Big(1+4\pi^2 m^2\mathrm{Ci}(2\pi m)\Bigr)
\end{align}
これを整理して、
$$\qquad \zeta(3)=\sum_{m=0}^{\infty}\Big(1+4\pi^2 m^2\mathrm{Ci}(2\pi m)\Bigr)$$
を得る。
お疲れ様でした。
グラフ
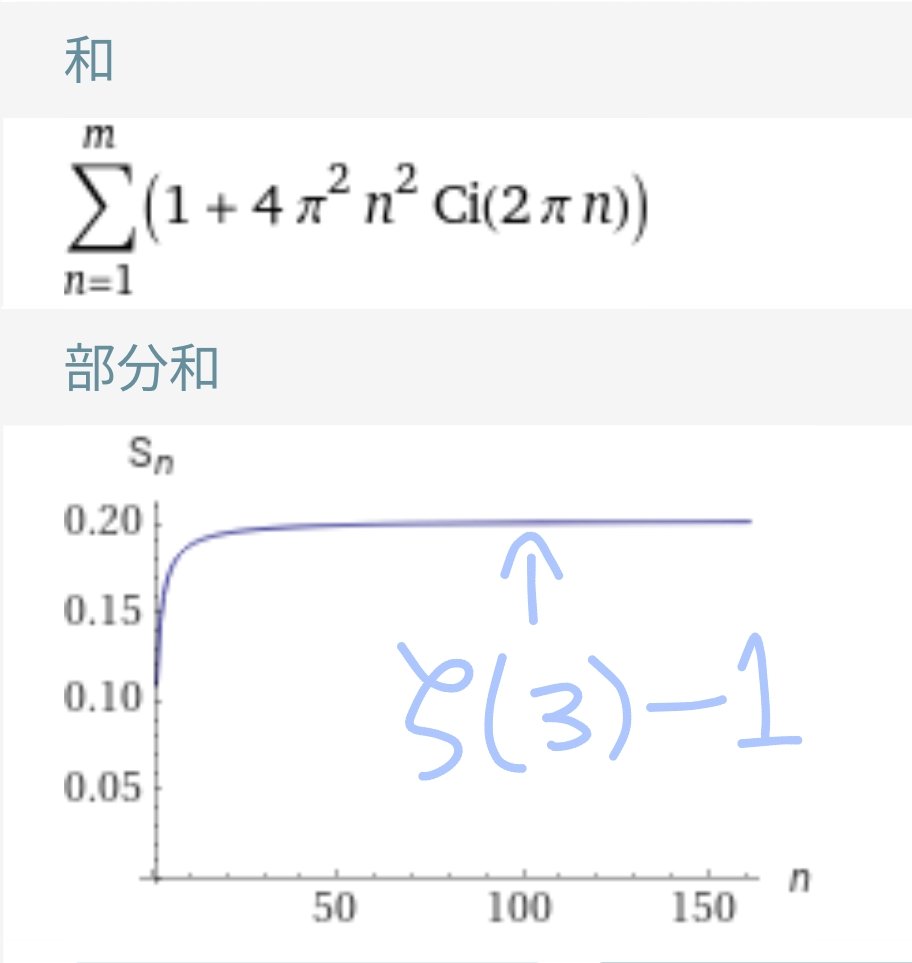 グラフ
グラフ
この議論の拡張を随時記事にしようと思います!
つづきの記事(未実装)
・一般の$\zeta(n)$への拡張!(未実装)
・多重対数関数への拡張!(未実装)
・二重ゼータへの拡張!(未実装)
