10分で分かる基本群〜取り急ぎ版〜
10分で分かる基本群
Intro
こんにちはしんぎゅらです!!今回は友達に聞かれた「基本群って何?」という質問にフランクに答えていこうと思います!!
まず、中学校では図形の合同、相似を習いましたよね?それらは、「図形の場所が違くても、形と大きさが同じなら同じ!!」「もう、大きさも違くていいから形が同じなら同じ!!」という条件を付けて図形を分類してきたはずです。
大学では位相空間論をやったよ〜という人もいるかもしれません。位相空間論は「連続変形で同じなら、同じ図形(=同相)でいいよ」というやつですね。今回は同相よりも弱い条件「ホモトピー同値」についての前段階に出てくる「基本群」についてベラベラ話していきます!!
ゆっくりしていってね
準備
以下$X$を位相空間とします。
閉区間$I=[0,1]$から$X$への連続写像$\omega :I\rightarrow X$が
$\omega (0)=x_0$かつ$\omega(1)=x_1$
となるとき$\omega$を$x_0$(←始点という)から$x_1$(←終点という)への道(path)という
$x_{0}$スタートで$x_{1}$ゴールの急にテレポーテーションしない道だと思えますね。Easy Easy
さて、この道に演算を与えてあげようと思います。
$ω_1$:$x_0$から$x_1$への道
$ω_2$:$x_1$から$x_2$への道
とするとき、$ω_1 \cdot ω_2$:$x_0$から$x_1$を経由して、$x_2$に向かう道と定義します
具体的には
$ω_1 \cdot ω_2= \begin{eqnarray}
\left\{
\begin{array}{l}
\omega_1 (2s)\text{ if }0 \leq s \leq \frac{1}{2}\\
\omega_2 (2s-1) \text{ if }\frac{1}{2} \leq s \leq 1
\end{array}
\right.
\end{eqnarray} $
とすれば、$x_{0}$から$x_{2}$への道になります。
ポイントとしては$\omega_1$の上を歩いてから$\omega_2$の道を歩いたという歩き方を決めているわけですね・
図1では$\omega_{1}$と$\omega_{2}$を繋げて歩いた道が$\omega_{1}\cdot\omega_{2}$になっています。
![よく見たら!FORMULA[29][1644233115][0]じゃなくて!FORMULA[30][38321][0]じゃん](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FNNdqZbwbgfQeKESpYffG.jpeg?alt=media) よく見たら$\omega$じゃなくて$w$じゃん
よく見たら$\omega$じゃなくて$w$じゃん
例えば、
・大阪から東京に向かう道
・東京から札幌に向かう道
が与えられている時に
大阪から東京経由で札幌に向かう道を構成しているわけです。
$X$上の関係$\sim$を以下で定義します
・$x\sim y \overset{\text{def}}{\Longleftrightarrow} \exists\omega$:$x$と$y$を結ぶ道
・この関係は同値関係になるのでその同値類を$X$の弧状連結成分という
・$X$の弧状連結成分が1つのとき、$X$を弧状連結という
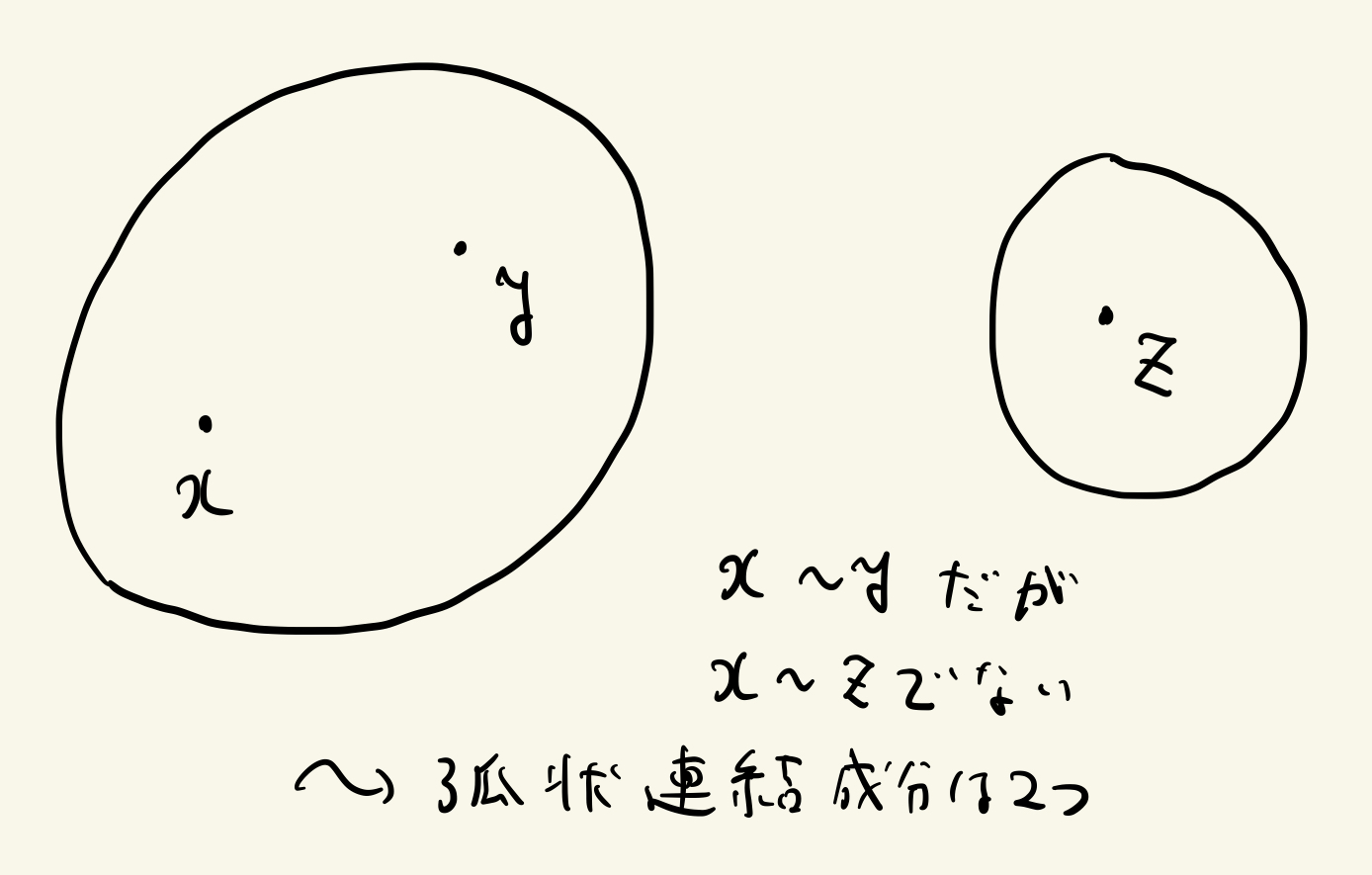 弧状連結の絵
弧状連結の絵
以下断りのない限り$X$は弧状連結とします。
ホモトピー
$x$を始点、$y$を終点とする2つの道を考える
$\omega : I\rightarrow X,\omega(0)=x$かつ$\omega (1)=y$
$\omega' : I\rightarrow X,\omega'(0)=x$かつ$\omega'(1)=y$
に対して、
$\omega_{t}:I\rightarrow X$で$\omega_{0}=\omega$かつ$\omega_{1}=\omega'$となるもので、$I\times I\rightarrow X;(s,t)\mapsto\omega_{t}(s)$が連続である連続写像の族$\{\omega_{t}\}_{t\in I}$が存在するとき、
$\omega$と$\omega'$はホモトープといい、$\omega_{t}$をホモトピーという。このとき$\omega \simeq \omega'$と表す
さていよいよ複雑になってきましたね、、、でも大丈夫!
絵で描けば簡単!!というより「やりたいこと」は実は明確なんです
赤の道$\omega$からオレンジの道$\omega_{\frac{1}{4}}$、緑の道$\omega_{\frac{1}{2}}$、水色の道$\omega_{\frac{3}{4}}$を経由して青の道$\omega'$に移っていますね
このように連続変形で片方の道からもう片方の道に移すことができるものをホモトープといいます
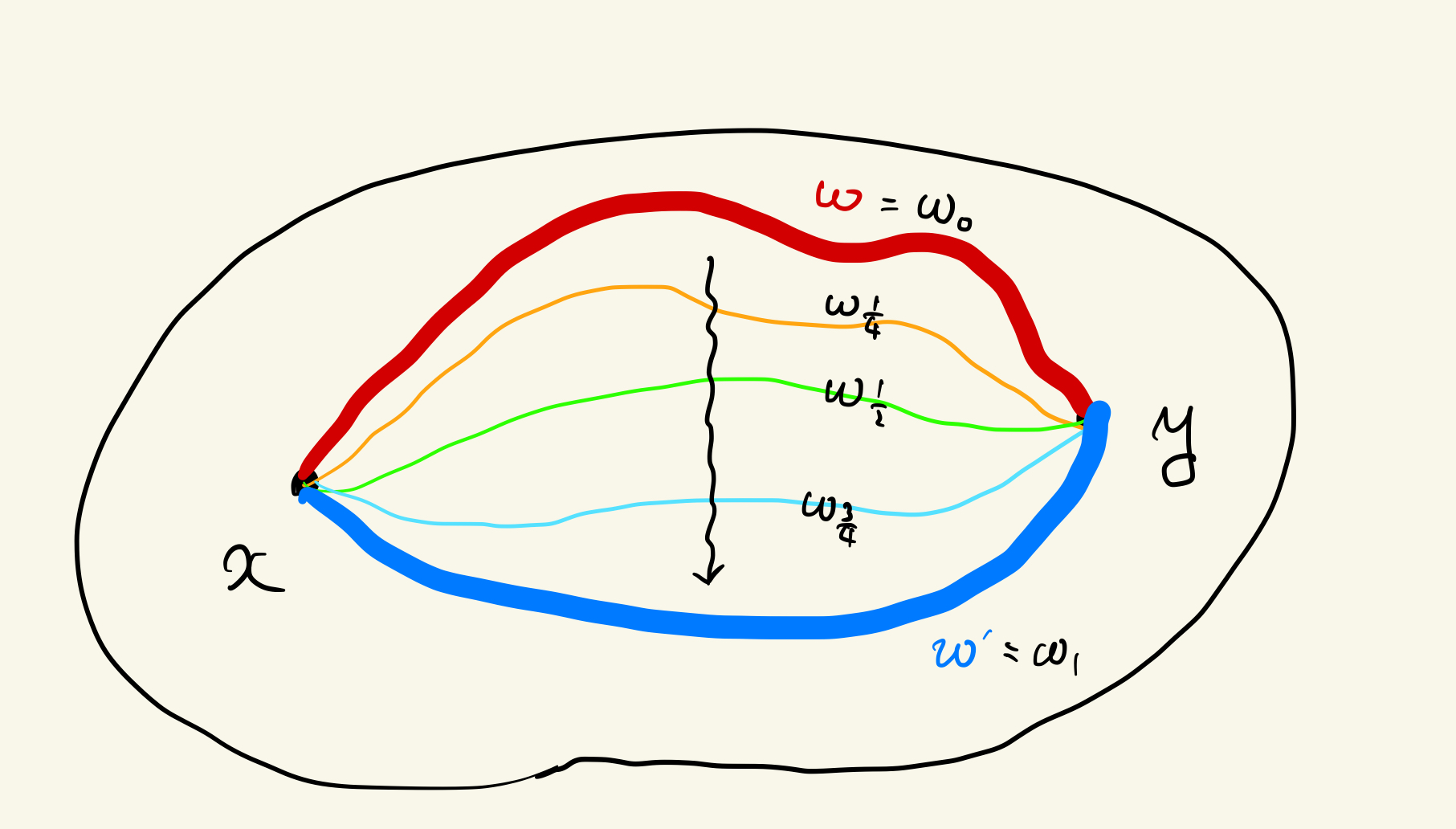 ホモトープ
ホモトープ
もうひとつホモトープでない例もいきましょう!
空間のド真ん中に立ち入り禁止エリアがありますね。これじゃァ例1のように赤の道を青の道に移せませんねェ〜
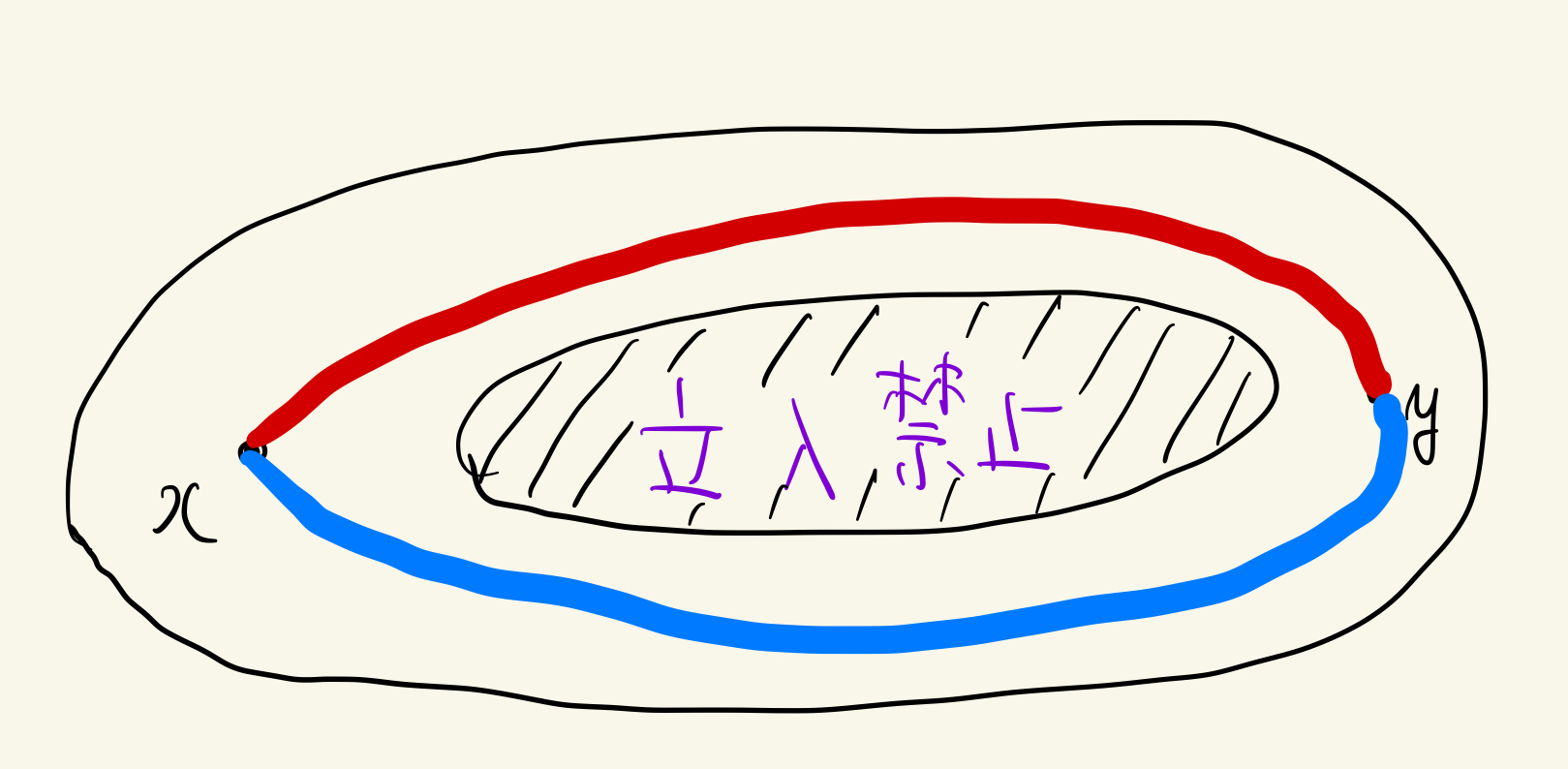 notホモトープ
notホモトープ
ホモトピーでない例を考えてみましょう!!
ヒント:図2をじーっと見てみてください
私がホモトピーを考える時は(伸び縮みする)紐の両端を固定して、動かせるかどうかを考えます。例1では赤の紐から青の紐まで動かせますが、例2では立ち入り禁止エリアの上を紐は通過できませんよね?
これがヒモトーp...ホモトープです!!
・始点と終点が一致してるとき、その点を基点という
・また、$x=y$なる2つの道$\omega,\omega'$がホモトープであるとき、$\omega$と$\omega'$は基点$x$を固定してホモトープという
$\Omega(X,x)$:$x$を基点とするXの閉じた道全体の集合
・$\pi_{1}(X,x)\overset{\text{def}}{=}\Omega(X,x)/\simeq$:ホモトープによる同値類全体
この$\pi(X,x)$を$x$を基点とするXの基本群という
・$\pi(X.x)$の元$[\omega]$を$x$を基点とする閉じた道$\omega$のホモトピー類という
閉じた道のことをループとも言います。
ある点を出発して戻ってきたルートの集まりのことですね。
ここで先ほど出した紐をイメージして考えてやると、とても易しくなります。
・まず自分のいる場所に紐の端っこを固定して周辺を散歩して、元々いた場所に戻ってきてください、その際は紐も持ったまま徘徊してください
・今手元には出発前に固定した紐の端とずっと持ってた紐の端がありますね。ここでコツなのが紐の両端を少し引っ張ってあげると今の散歩の最短ルートが分かります(この引っ張る作業が「ホモトープによる類別(=同じっぽい道を同じ道としている)」になります)
基本群って群なの?
ここで代数、特に群論を学んだ方は気になると思います。
お前、群なの?
答えはYesです
では群の定義の確認からしましょう
$G$を空でない集合
$\cdot$を$G\times G\rightarrow G$を$G$で閉じた演算とする
以下の3つの条件を満たす時、$(G,\cdot)$を群という
(1)$\forall x,y,z\in G, (x\cdot y)\cdot z=x\cdot(y\cdot z)$結合則
(2)$\exists e\in G$ s.t.$\forall x\in G,e\cdot x=x\cdot e=x$単位元
(3)$\forall x\in G,\exists y\in G$s.t.$x\cdot y=y\cdot x=e$逆元
懐かしいですね〜〜一応具体例もあげときますね〜〜
・整数全体$\mathbb{Z}$は加法に関して群をなすが、乗法に関して群をなさない
・有理数全体$\mathbb{Q}$は加法に関して群をなし、有理数全体から$0$を除いたもの$\mathbb{Q}^{*}$は乗法に関して群をなす
・正三角形をぐるぐる回すやつも群をなす(二面体群という)
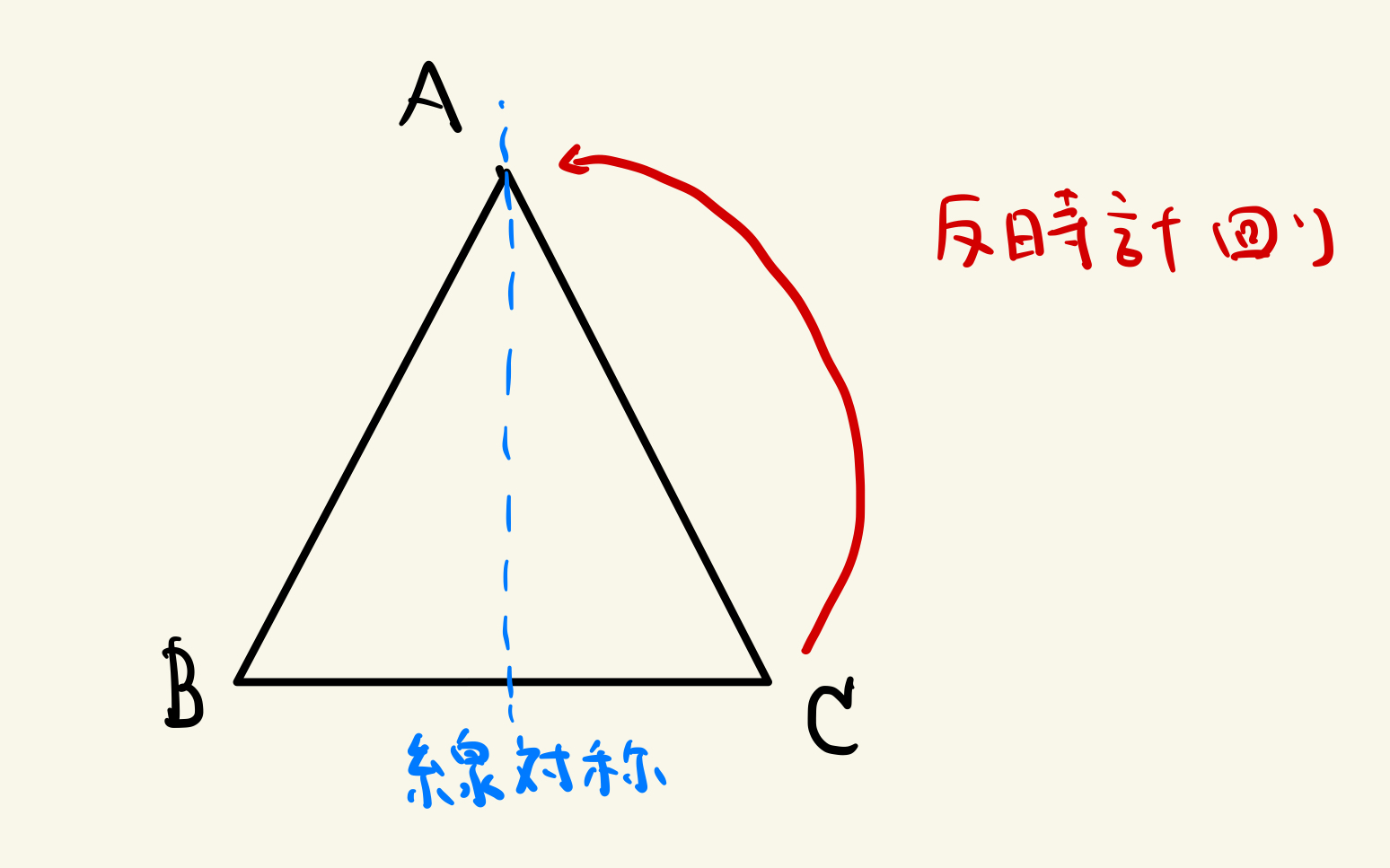 ぐるぐる回すやつ
ぐるぐる回すやつ
$\forall x,y\in G, x\cdot y=y\cdot x$
を満たすとき$(G,\cdot)$を可換群もしくはAbel群という
さて、本題に戻りましょう
基本群に「道の合成」を与えてみましょう
・結合則については自明ではありませんが、絵を描いてみて自然だなと納得してください。証明も難しくありませんが、私が面倒なので飛ばします。
さて、単位元はどうでしょうか?
単位元というのは集合の元に作用しても何も変わらないことです。整数の加法で言えば0、有理数の乗法で言えば1、二面体群で言えば動かさないですよね。
タッカーが嫌いそうな勘のいいガキの皆さんはお気づきでしょうか?
そうです。動かないという道ですね!!さっきの紐の例で言うと両端から紐を回収したら全部戻ってきたやつですね!!
 単位元の道(回収できる)
単位元の道(回収できる)
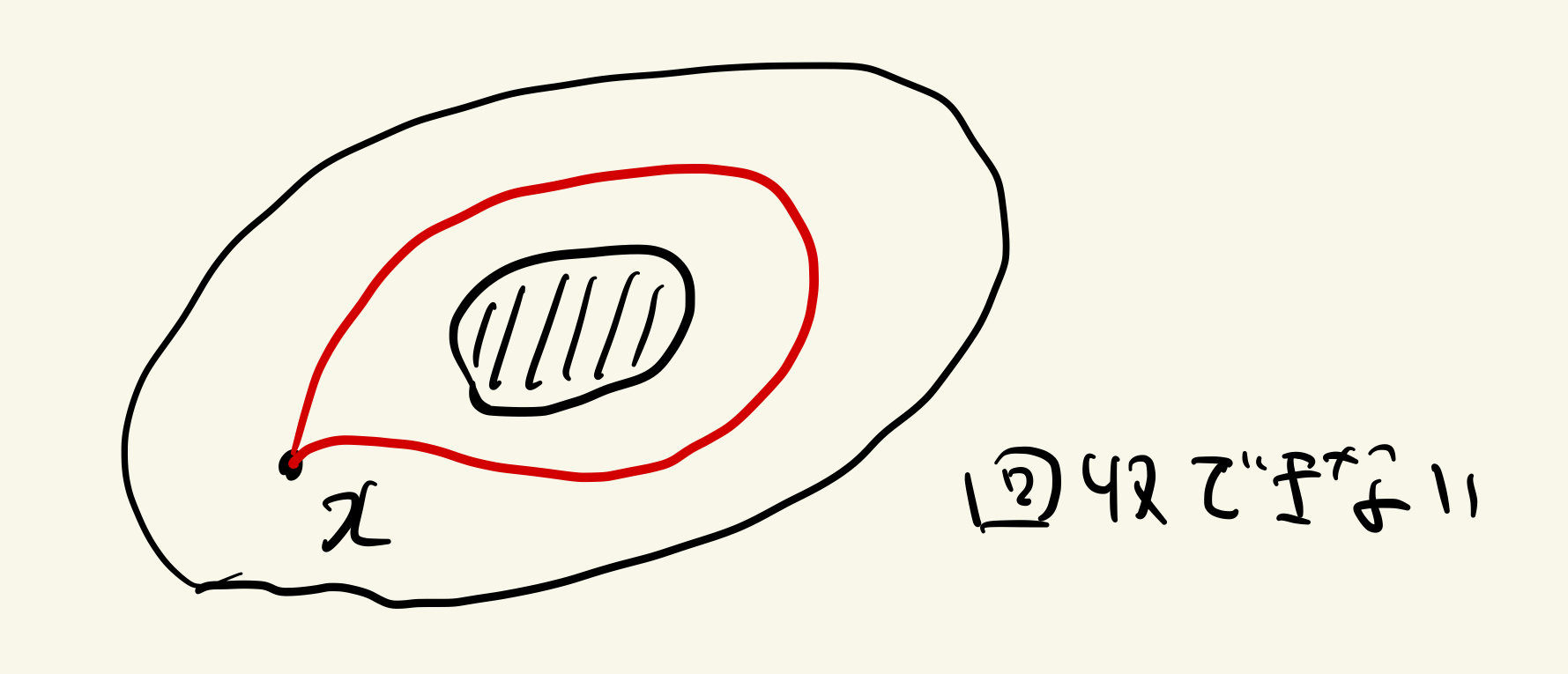 回収できてない
回収できてない
・ここまで来れば逆元は簡単です。来た道を戻ればいいんですから。赤の道の逆は青の道ですね!!
 逆の道
逆の道
もう分かった通り、基本群は群になりますね!!
具体例三昧
$D^{2}=\{x\in\mathbb{R}^{2}| \left\| x \right\|\leq1 \}$:円盤の基本群は自明な群$\{e\}$と同型
$\because$任意のループは動かないのと同じ
$\mathbb{R}^{2}$上の1点集合$\{x\}$の基本群は自明な群$\{e\}$と同型
基本群が自明な群であるとき、位相空間$X$を単連結という
例4、例5の位相空間は単連結
平面ドーナッツことアニュラス$A=\{x\in\mathbb{R}^{2}|1<\left\|x\right\|\leq2\}$の基本群は$\mathbb{Z}$と同型
$\because$穴の周りを時計回りした時に+1周、反時計回りを-1周とすれば、ループは戻ってくるまで穴の周りを何周したかという情報に書き換えられます。
何周したか?と聞かれたら、整数値で答えますよね?
だから基本群は$\mathbb{Z}$と同型!!
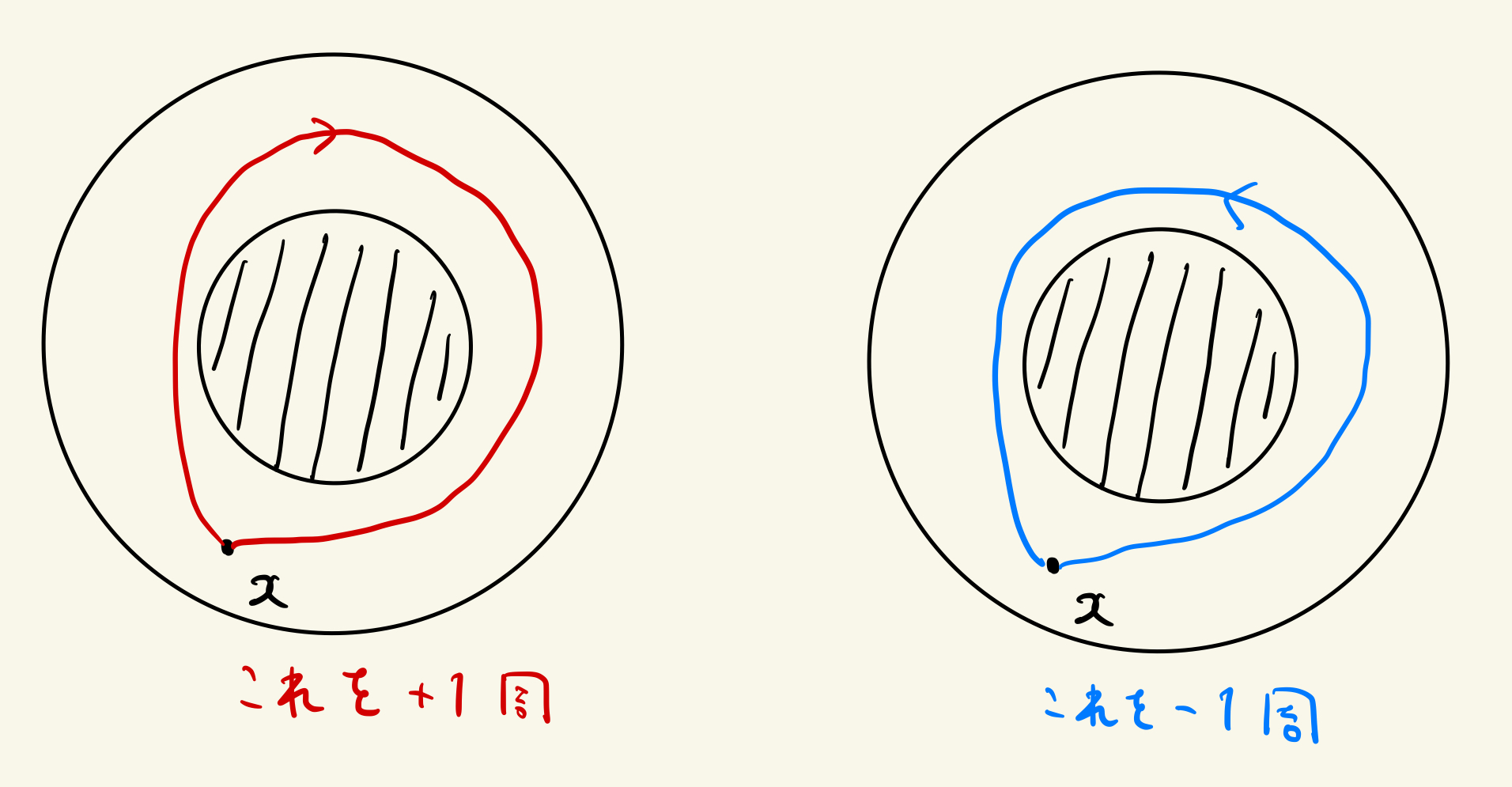 アニュラス
アニュラス
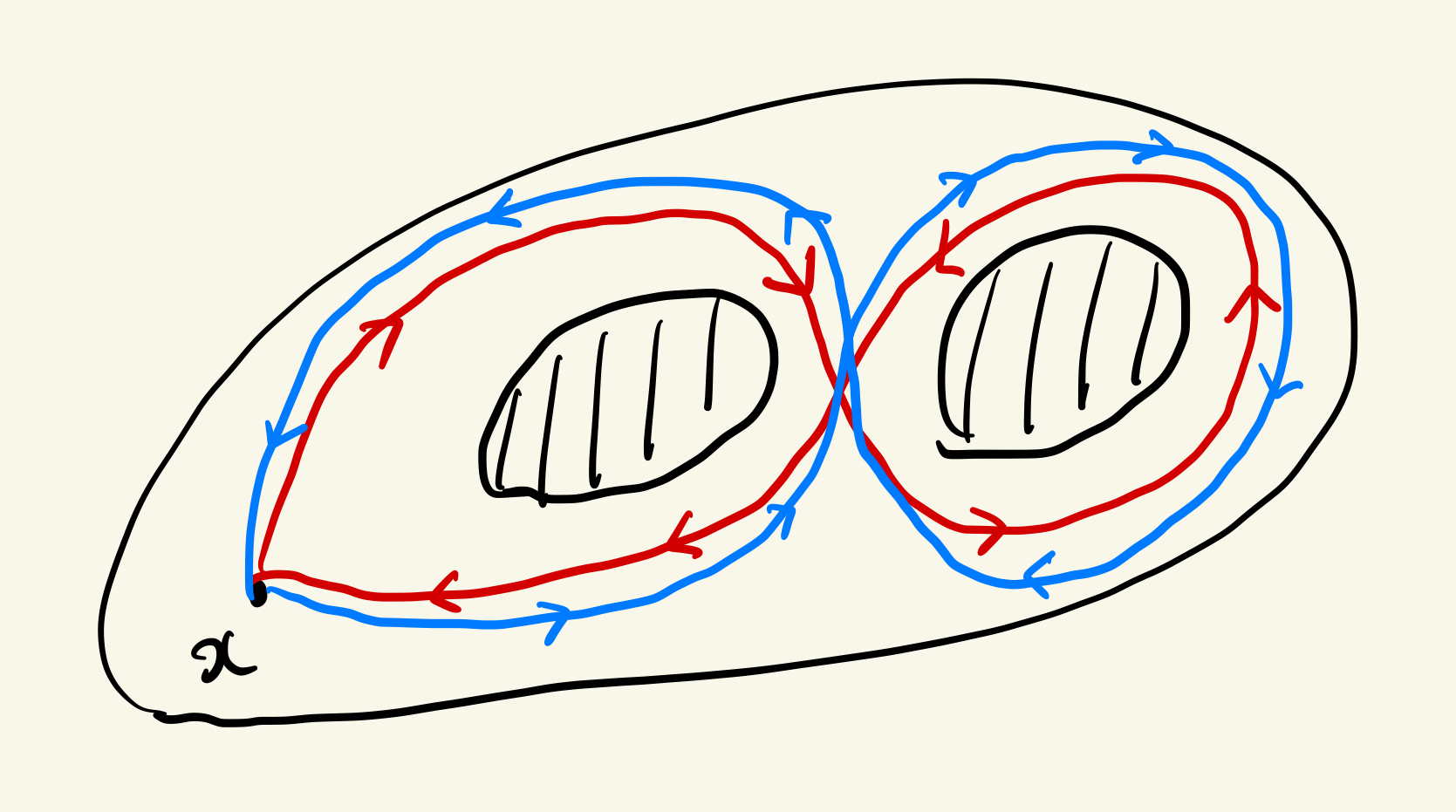
では穴が$n$個ある平面ドーナッツの基本群はどうなるでしょう?
まとめ
位相空間の分類をしたり、特徴を抜き出そうとしたら、やはり連続が大事ですよね。これが連続性を大事にすると御利益がある学問、位相幾何学です。
