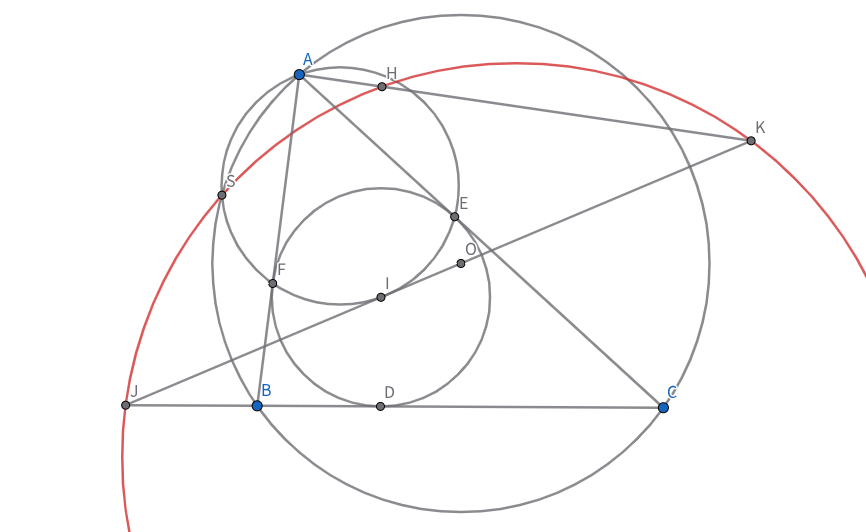
比較的有名事実の証明
katsuo_templeです.今回は, Xに投稿 したこの問題の証明を書こうと思います.比較的有名事実らしいので,別証があれば教えていただけると嬉しいです.
本編
さて,今回の記事では以下の問題を示していこうと思います.
三角形$ABC$において,その内心を$I$,外接円を$Γ$とする.三角形$ABC$のフォイエルバッハ双曲線と$Γ$の第四交点を$Z$とし,三角形$BIC$の垂心を$H_I$とする.$AI$を直径とする円と$Γ$が再び交わる点を$S$としたとき,三点$S,H_I,Z$は同一直線上にあることを示せ.
まず初めに,いくつかの補題を示していこうと思います.
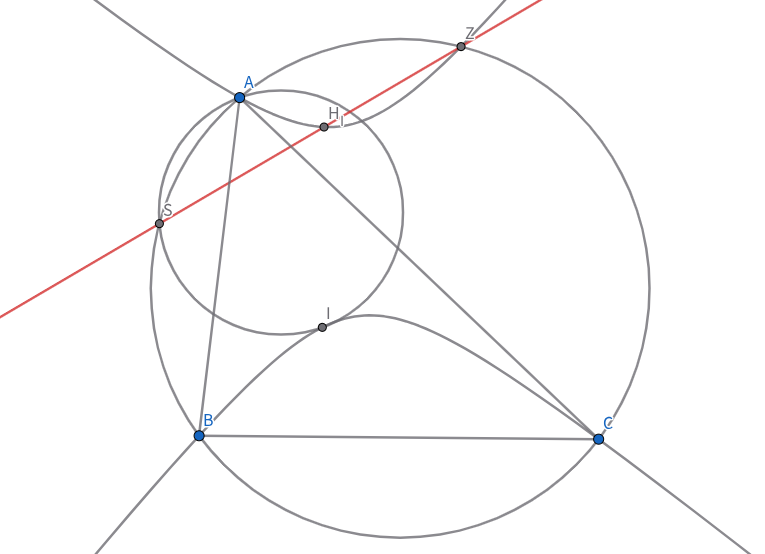
三角形$ABC$において,内接円を$ω$,内心を$I$,$I$から$BC$に下ろした垂線の足を$D$とする.$A$から$ID$に下ろした垂線の足を$K$,三角形$BIC$の垂心を$H_I$としたとき,$H_I$は$ω$による反転で$DK$の中点に移る.
$ω$と$CA,AB$との接点をそれぞれ$E,F$とする.$DK$の中点を$M$としたとき,$IM×IH_I=ID^2$を示せば良い.$I$について$D$と対称な点を$D'$とし,$DE∩D'F=P,DF∩D'E=Q$とすると,パスカルの定理から$P,Q,A$は同一直線上にあり,特に$D'$は三角形$DPQ$の垂心である.よって,$K$は$D$から$PQ$に下ろした垂線の足であり,$PQ//BC$.したがって,$\measuredangle QPD=\measuredangle CDE=90°-\measuredangle ICB=\measuredangle H_IBC$.同様にして,$\measuredangle DQP=\measuredangle H_ICB$.よって,$H_IBCID∽DPQD'K$.この相似から$DD'×DH_I=IH_I×DK$を得る.あとは適切な式変形を行うことで,$IM×IH_I=ID^2$を得ることができる.
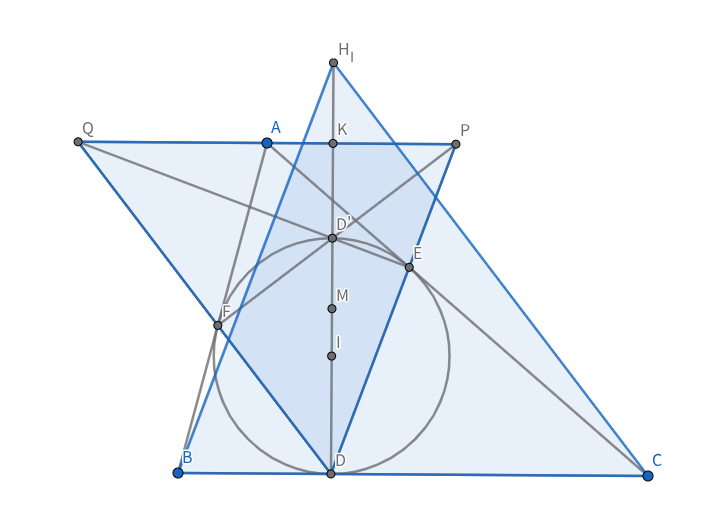
三角形$ABC$において,外接円を$Γ$,内心を$I$,外心を$O$とする.三角形$ABC$のフォイエルバッハ双曲線と$Γ$の第四交点を$Z$とし,$OI$について$A$と対称な点を$A_1$とするとき,$BC⊥ZA_1$.
三角形$ABC$のフォイエルバッハ点を$Fe$とし,$AZ∩OI=R$とする.$Fe$は三角形$ABC$における$OI$のorthopoleであるから,$FeR⊥BC$.また,$Fe$はフォイエルバッハ双曲線の中心であり,三角形$ABC$の九点円上にあるので,$Fe$は$HZ$の中点である.よって,$R$が$AA_1$の中点であることをあわせることで,$ZA_1⊥BC$が従う.
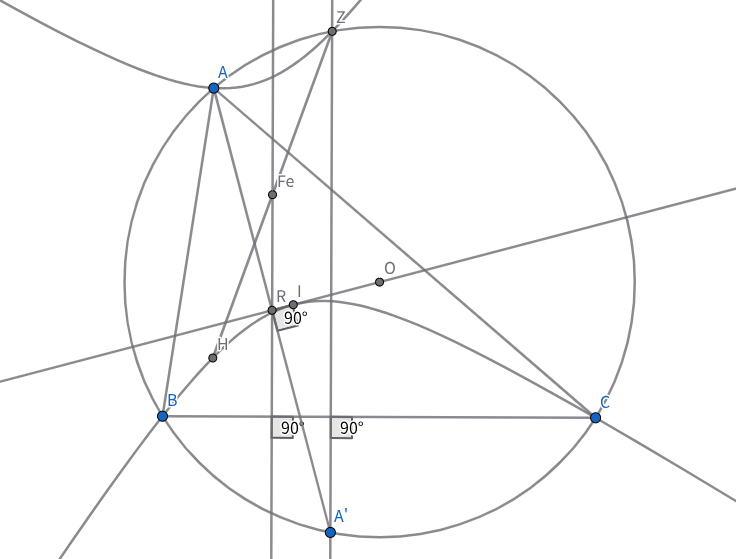
三角形$ABC$において,内心を$I$,外接円を$Γ$とする.$AI$を直径とする円と$Γ$が再び交わる点を$S$とし,$I$から$BC$に下ろした垂線の足を$D$とすると,$SD$は$Γ$における$A$を含まない弧$BC$の中点$N$を通る.
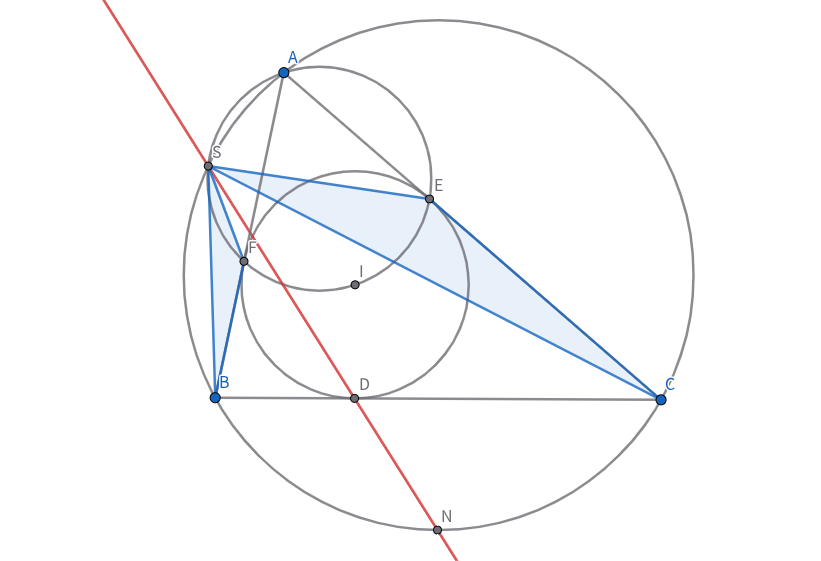
$I$から$CA,AB$に下ろした垂線の足をそれぞれ$E,F$とすると,$E,F$は$AI$を直径とする円上にある.よって,簡単な角度追跡から$△SBF∽△SCE$.したがって,$\dfrac{SB}{SC}=\dfrac{BF}{CE}=\dfrac{BD}{CD}$.よって,$SD$は$\angle BSC$の二等分線であり,これは$N$を通る.
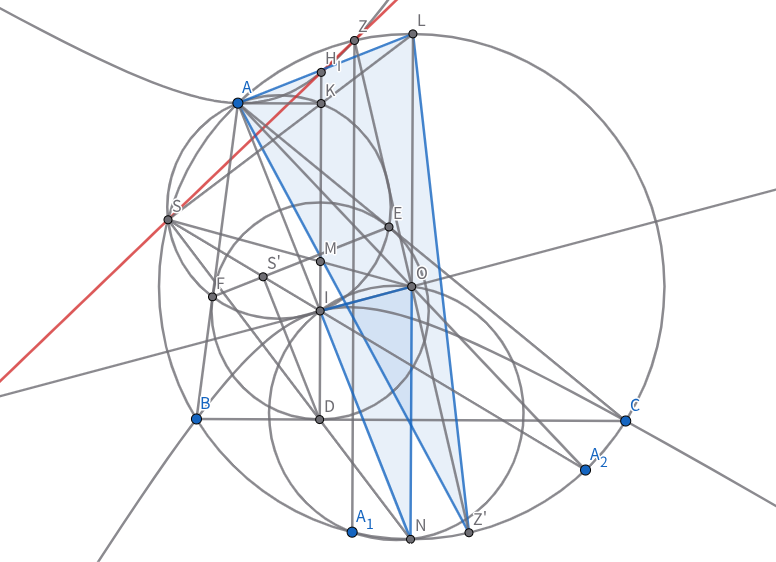
$I$から$BC,CA,AB$に下ろした垂線の足をそれぞれ$D,E,F$とし,$A$から$ID$に下ろした垂線の足を$K$とする.さらに$Γ$における$A$を含まない弧$BC$の中点を$N$,$A$を含む弧$BC$の中点を$L$とする.このとき,補題3より三点$S,D,N$は同一直線上にある.また,$K$は$AI$を直径とする円上にあるので,簡単な角度追跡から三点$S,K,L$は同一直線上にある.ここで,三角形$ABC$の内接円で反転すると,補題1より$H_I$は$DK$の中点$M$に移り,$S$は$D$から$EF$に下ろした垂線の足$S'$に移る.三角形$ABC$の外心を$O$とすると,$O$は$NL$の中点であるから三点$S,M,O$は同一直線上にあり,また$S'D//IN$.よって,$\dfrac{SD}{DN}=\dfrac{SS’}{SI}=\dfrac{SM}{MO}$.これと四点$H_I,S,S',M$が同一円周上にあることをあわせることで,$\measuredangle ISH_I=\measuredangle ION$を得る.
$OI$について$A$と対称な点を$A_1$とすると,$\measuredangle ONI=\measuredangle IAO=\measuredangle OA_1I$なので,四点$A_1,I,O,N$は同一円周上にある.$O$に関して$Z$と対称な点を$Z'$とすると,補題2より$Z,Z'$は$NL$に関して対称である.よって,簡単な角度追跡から$△INO∽△AZ'L$.したがって,$\measuredangle ION=\measuredangle ALZ'$.また,有名事実より$O$について$A$と対称な点を$A_2$とすると,三点$S,I,A_2$は同一直線上にある.よって,簡単な角度追跡から$\measuredangle ALZ'=\measuredangle ISZ$を得る.以上より,$\measuredangle ISH_I=\measuredangle ISZ$を得るので,三点$S,H_I,Z$は同一直線上にある.
さいごに
初等幾何で証明しましたが,もっと見通しの良い解法がありそう...
三角比を使えば容易く証明できるっぽいですね...
この構図が使える問題があれば随時書いておきます.
三角形$ABC$において,外心を$O$,内心を$I$とする.三角形$ABC$の内接円と$AC,AB$との接点をそれぞれ$E,F$とし,三角形$BIC$の垂心を$H$とする.円$ABC$と円$AEF$が再び交わる点を$S$とし,$OI$と$BC,AH$の交点をそれぞれ$J,K$とするとき,四点$H,K,J,S$は同一円周上にあることを示せ.