フェルマー点と等力点の鏡映における関係
始めに
初投稿です。
全ての角が$120°$未満である$\triangle ABC$について
・$\triangle ABC$の第二フェルマー点を$P_{2}$,第一等力点を$P_{1}'$としたとき、
$\triangle P_{1}'BC,\triangle P_{1}'CA,\triangle P_{1}'AB$のそれぞれの第二フェルマー点と$P_{2} $は、$\triangle ABC$の第一等力点を中心に同一円周上にある。
・$△ABC$の第一フェルマー点を$P_{1}$としたとき、
$\triangle P_{1}'BC,\triangle P_{1}'CA,\triangle P_{1}'AB$のそれぞれの第一フェルマー点と$P_1 $は、$△ABC$の第一ナポレオン点を中心に同一円周上にある。
この命題は図形描画サイトでシフラー点のようなことができないか試していた時に偶然発見したものです。有用性の欠片もないですね。
$\triangle ABC$において、
三角形の外側に、正三角形$BDC,CEA,AGF$を書いたとき、
$AD,BE,CF$は一点で交わりその点を「第一フェルマー点」という。
三角形の内側に、同様にして出来た点を「第ニフェルマー点」という。
またそれぞれの等角共役点を「第一等力点」「第二等力点」という。
しかし、$120°<∠A$などのときは、$P_{1}'$が$△ABC$から出てしまうので$120°$未満の時と連続的になるように考える必要があります。なのでここでは$ \triangle P'_{1}BC,P'_{1}CA,P'_{1}AB$のフェルマー点に新たな定義を採用します。
上記の様に$D,E,F$を取る。
それぞれ、円$DBC,ECA,FAB$と$PD,PE,PF$の$D,E,F$でない方の交点を$ \triangle P'_{1}BC,P'_{1}CA,P'_{1}AB$の第一フェルマー点とする。
第二フェルマー点についても同様です。一般の点$P$における$\triangle DEF$をCirclecevian triangleと呼ぶそうです。
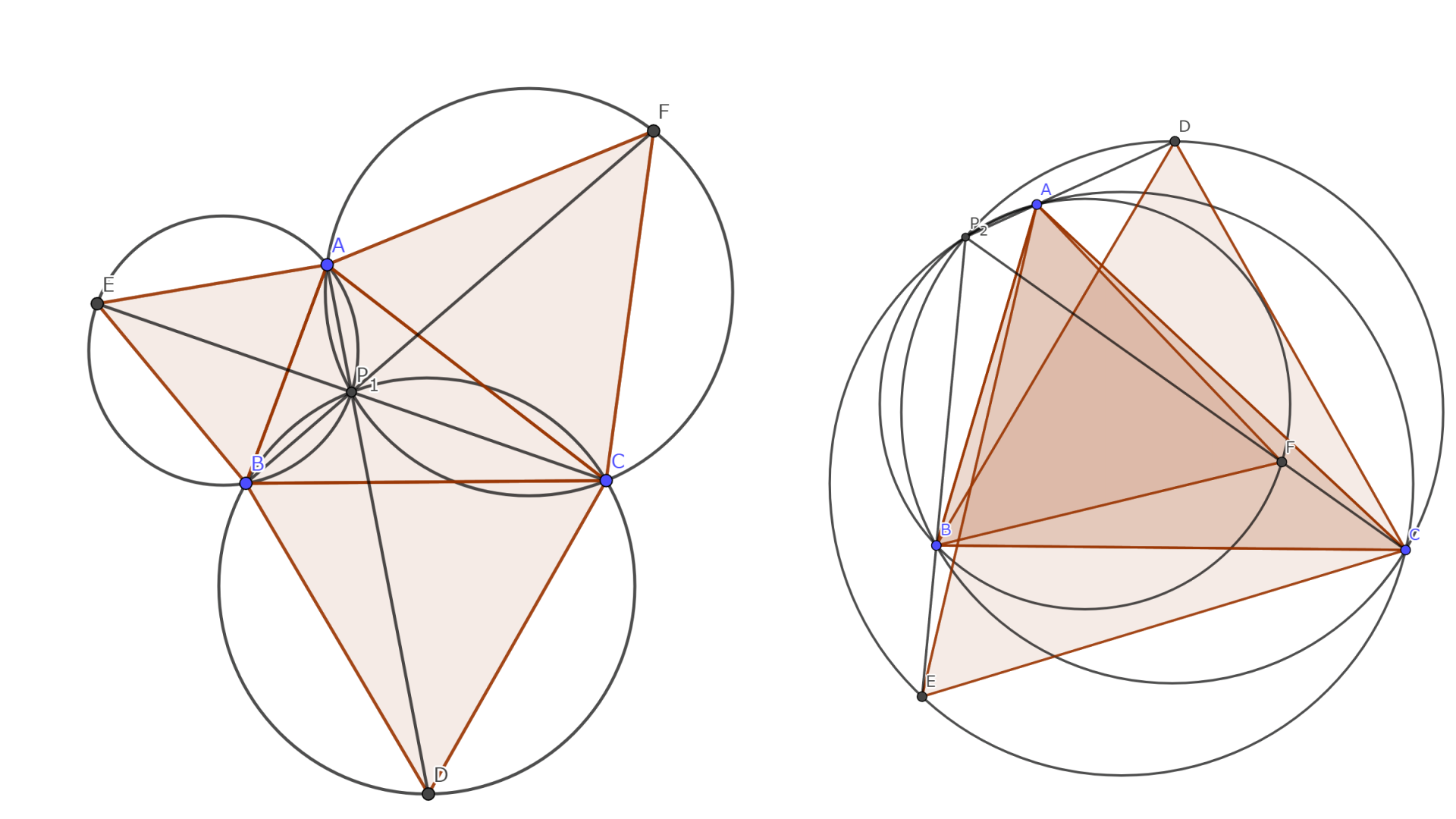 フェルマー点の図示
フェルマー点の図示
証明
補題
第一等力点についていくつかの表し方をします。
三点$A,B,C$についてそれぞれ$BC,CA,AB$についての3つのアポロニウスの円の交点は第一、第二等力点である。
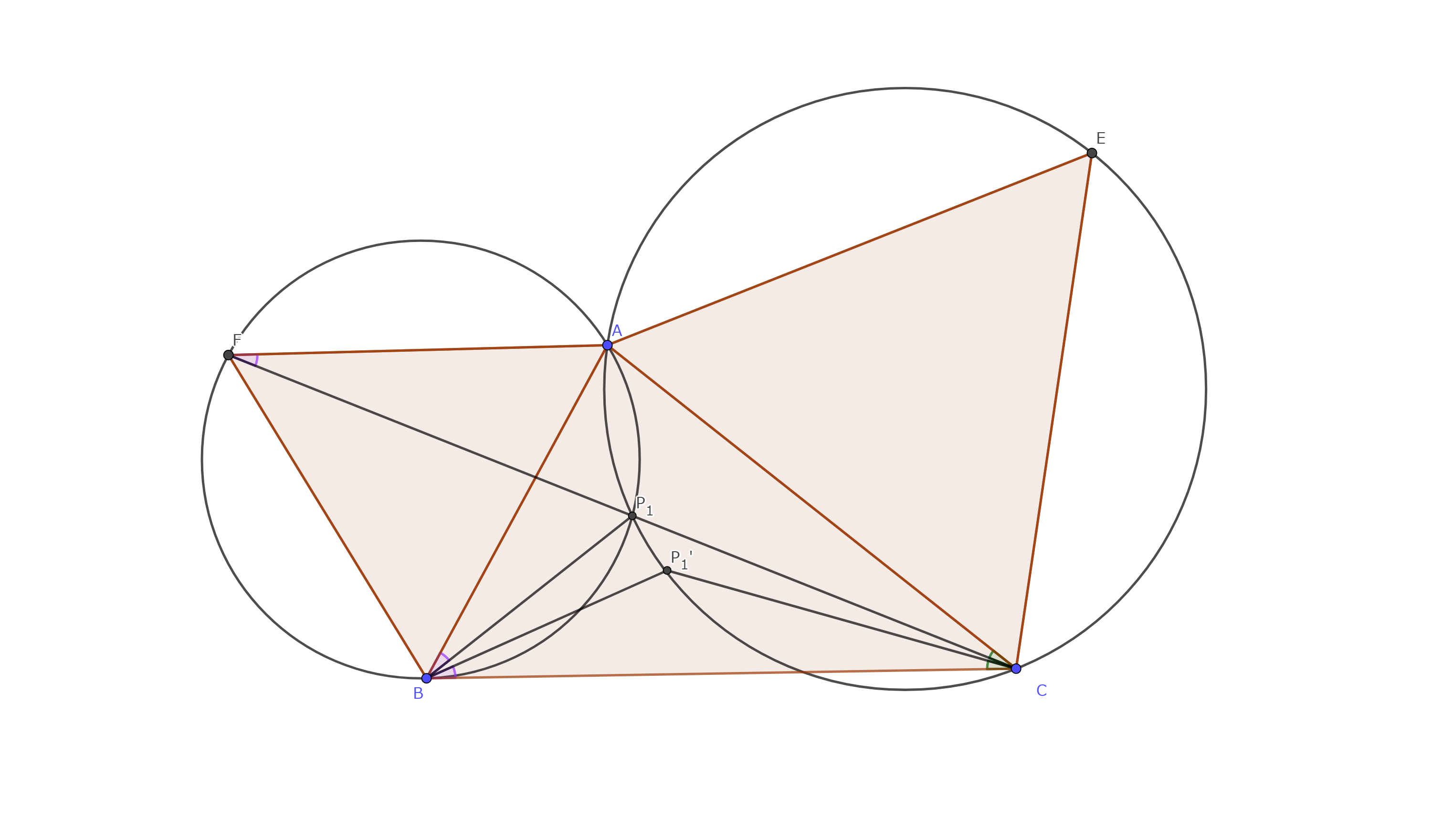
$P_{1}$を第一フェルマー点、$P_{1}'$を第一等力点とする。
$\triangle ABC$の外側に正三角形$BDC,CEA,AFC$を描く。
図2において等角共役の定義より$∠P_{1}'BC=∠P_{1}BA,∠P_{1}'CB=∠ACF$
円周角の定理より$∠P_{1}BC=∠AFC$
よって$\triangle AFC\backsim\triangle P_{1}'BC$であるので$P_{1}'B:P_{1}'C=AF:AC=AB:AC$.
同様にして$P_{1}'A:P_{1}'C=CA:CB,P_{1}'A:P_{1}'B=CA:CB$.
アポロニウスの円の定義より$P_{1}'$は3つのアポロニウスの円周上にある。
第二フェルマー点と第二等力点でも同様にして証明できます。
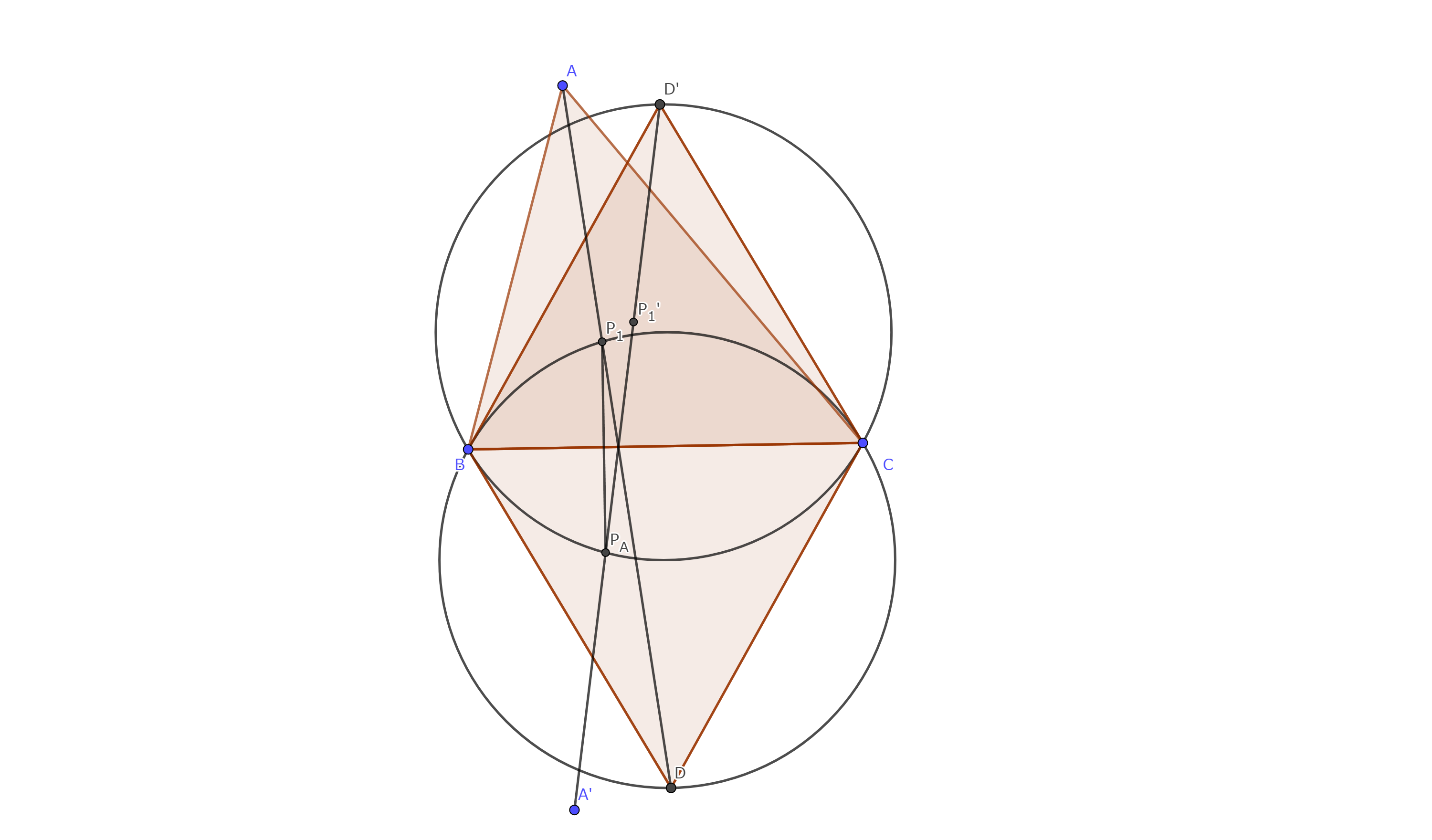
$A,B,C$をそれぞれ$BC,CA,AB$に対して鏡映した点$A',B',C'$と、
三角形の内側に正三角形$BD'C,CE'A,AF'B$を書いたとき、
$A'D',B'E',C'F'$は一点で交わりその点は$P_{1}'$である。
$A'B:A'C=AB:AC$より$A'$もアポロニウスの円上にある。
$P'$は等力点なので$\triangle ABD\equiv \triangle A'BD'$より$\triangle BCD'$は正三角形
$B,C$も同様にして、$\triangle BD'C,\triangle CE'A,\triangle AF'B$は正三角形となり定理の作図と一致する。

$\triangle P_{1}'BC$の第二フェルマー点は$P_{1}$を$BC$に対して鏡映した点である。
補題3より$P_{1}$を$BC$で鏡映させた点は$\triangle P_{1}'BC$の第二フェルマー点である。
本題
$\triangle ABC$の第二フェルマー点$P_{2}$,第一等力点$P_{1}'$としたとき、
$\triangle P_{1}'BC,\triangle P_{1}'CA,\triangle P_{1}'AB$のそれぞれの第二フェルマー点と$P_{2}$は、$P_{1}'$を中心に同一円周上にある。
$△P_{1}'BC,△P_{1}'CA,△P_{1}'AB$の第二フェルマー点をそれぞれ$P_{A},P_{B},P_{C}$とする。
$∠P_{A}P_{2}P_{C}$
$=∠P_{A}P_{2}B+∠P_{C}P_{2}B$
$=∠P_{A}F'B+∠P_{C}D'B$
$=∠P_{1}FB+∠P_{1}DB$
$=∠P_{1}FC+∠P_{1}CB$
$=120°-∠B$

また、等角共役の性質より$\triangle P_{A}P_{B}P_{C}$の外心は$P_{1}'$である。
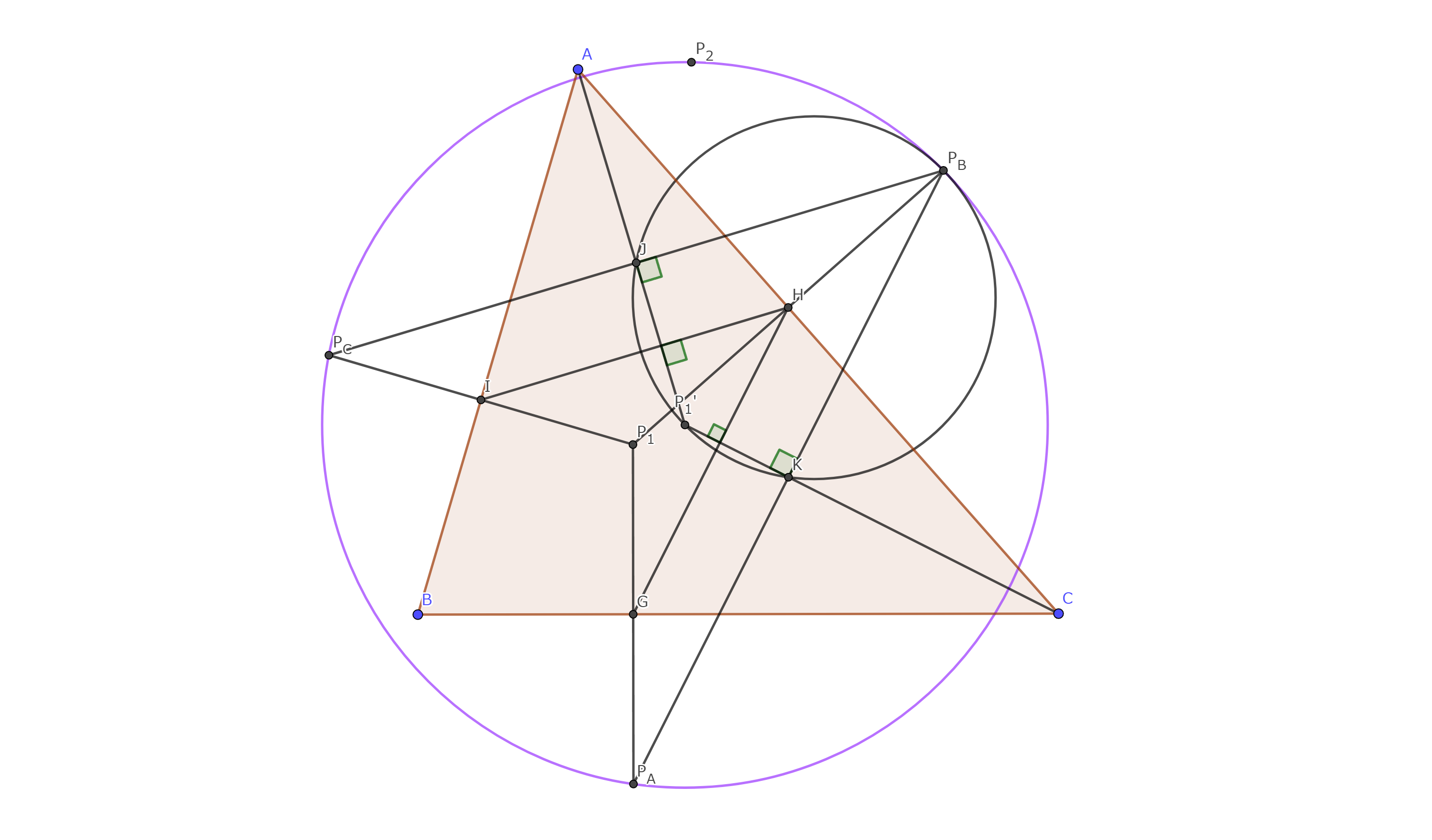
$P_{1}$の$BC,CA,AB$に対する垂足をそれぞれ$G,H,I$とすると
再び等角共役の性質より$AP_{1}'\perp HI,CP_{1}'\perp HG.$
中点連結定理より$ HI /\!/P_{B}P_{C}, HG /\!/P_{A}P_{B}.$
したがって$AP_{1}'\perp P_{B}P_{C},CP_{1}'\perp P_{B}P_{A}.$
$P_{B}P_{C} $と$AP_{1}',P_{A}P_{B} $と$CP_{1}'$の交点をそれぞれ$J,K$とすると
$P_{1}',J,K,P_{B}$は共円なので
$∠P_{A}P_{B}P_{C}$
$=180°-∠AP_{1}'C$
$=180°-(60°+∠B) \qquad (\because△AP_{1}'C \equiv △ABD )$
$=120°-B.$
よって$∠P_{A}P_{2}P_{C}=∠P_{A}P_{B}P_{C}$なので
円周角の定理の逆より題意は示された。
追記
$Antigonal$なるものがあるそうです。
参照
の定義3を引用します。
ある点$P$を$BC,CA,AB$で鏡映した点をそれぞれ$A',B',C'$とすると、
円$ A'BC,B'CA,C'AB $は一点で交わり、その点を$Antigonal\ point$という。
$Antigonal\ point,A',B',C'$は共円でその中心は$P$の等角共役点である。
(全て有向角で扱う。)
・円$A'BC,C'AB$の交点を$Q$とすると、
$\angle CQA=\angle CQB+\angle BQA=\angle CA'B+\angle BC'A=\angle BPC+\angle APB =\angle APC=\angle CB'A $より、
円$ A'BC,B'CA,C'AB $は一点で交わる。
・図8の構図と同様にして$P$の等角共役点を$P'$とすれば、
$\angle A'QC'=\angle A'QB+\angle BQC'=\angle A'CB+\angle BAC'$
$=\angle BCP+\angle PAB =\angle ACP'+\angle P'AC=\angle AP'C=\angle AB'C$
より$Q(Antigonal\ point),A',B',C'$は共円。
閑話休題。
$\triangle P_{1}'BC,\triangle P_{1}'CA,\triangle P_{1}'AB$のそれぞれの第一フェルマー点と$P_1 $は、
$\triangle ABC$の第一ナポレオン点を中心に同一円周上にある。
$△P_{1}'BC$の第一フェルマー点を$Q$とする。
補題4より$P_{B},P_{C},P_{1}$は$A$を中心とし、同一円周上にある。
よって$∠P_{B}AP_{C}=2∠A$より$∠P_{B}P_{1}P_{C}=180°-∠A.$
また、$AP_{C}$と円$P_{C}BQP_{1}'$の、$P_{C}$でない方の交点を$L$とすると、
$P_{C}$の定義より$△BP_{1}'L$は正三角形なので$P_{1}'L=P_{1}'B$
補題2より$AP_{1}':BP_{1}'=b:a$
$∠AP_{1}'L=∠C+60°-60°=∠C$より$△AP_{1}'L \backsim △ABC$
したがって$∠P_{1}'QP_{C}=∠ALP_{1}=∠B$
同様にして$∠P_{1}'QP_{B}=∠C$
よって$∠P_{B}QP_{C}=∠B+∠C=180°-∠A$より
$P_{B},P_{C},P_{1},Q$は$A$を中心とし、同一円周上にある。
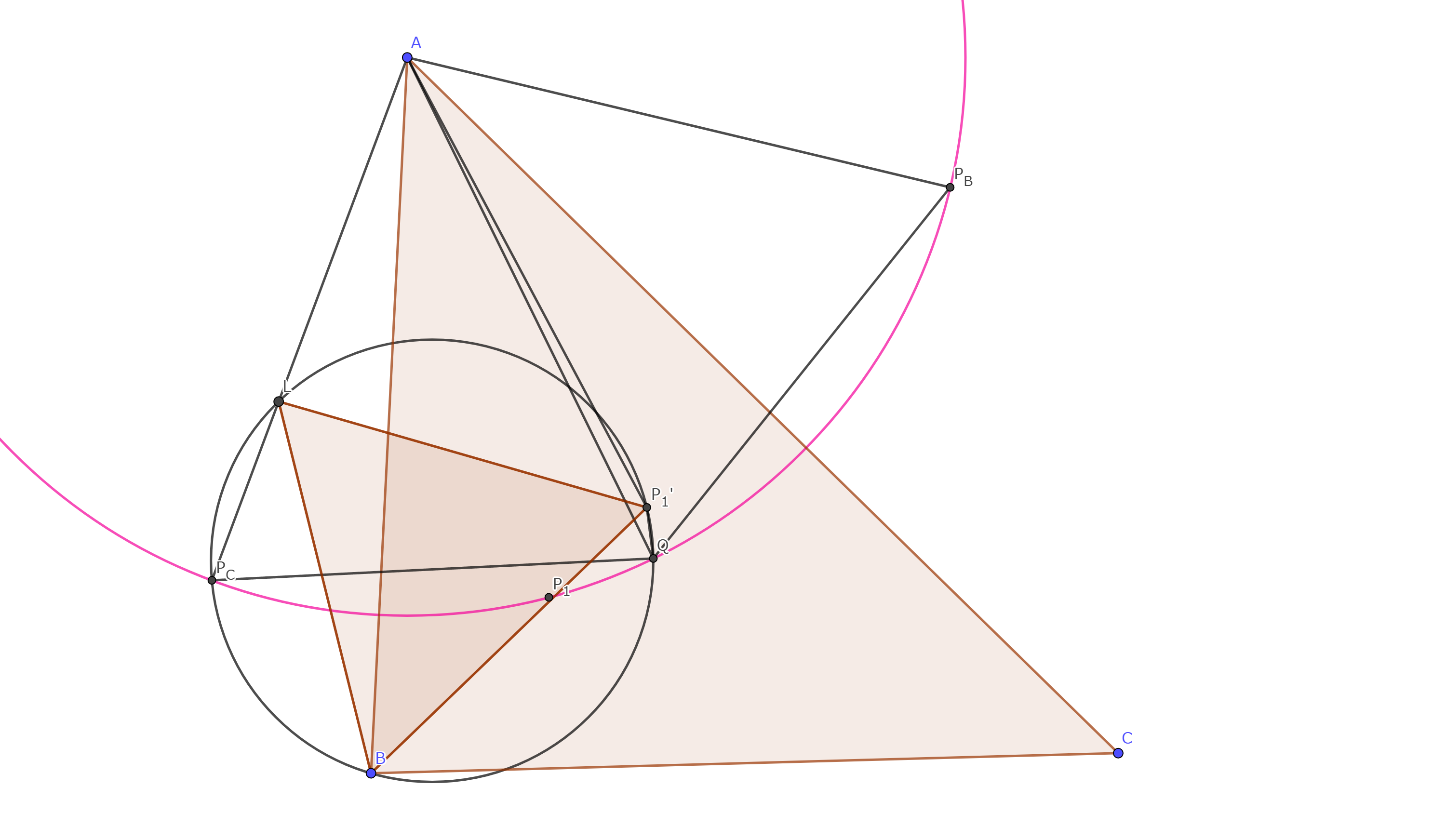
また$P_{1},Q$は円$BDC$上にあるので
$P_{1},Q$の垂直二等分線は$A$と正三角形$BDC$の中心を通る。
$\triangle P_{1}'CA,\triangle P_{1}'AB$の第一フェルマー点でも同様にして
それら3つの垂直二等分線は第一ナポレオン点で交わるので題意は示された。
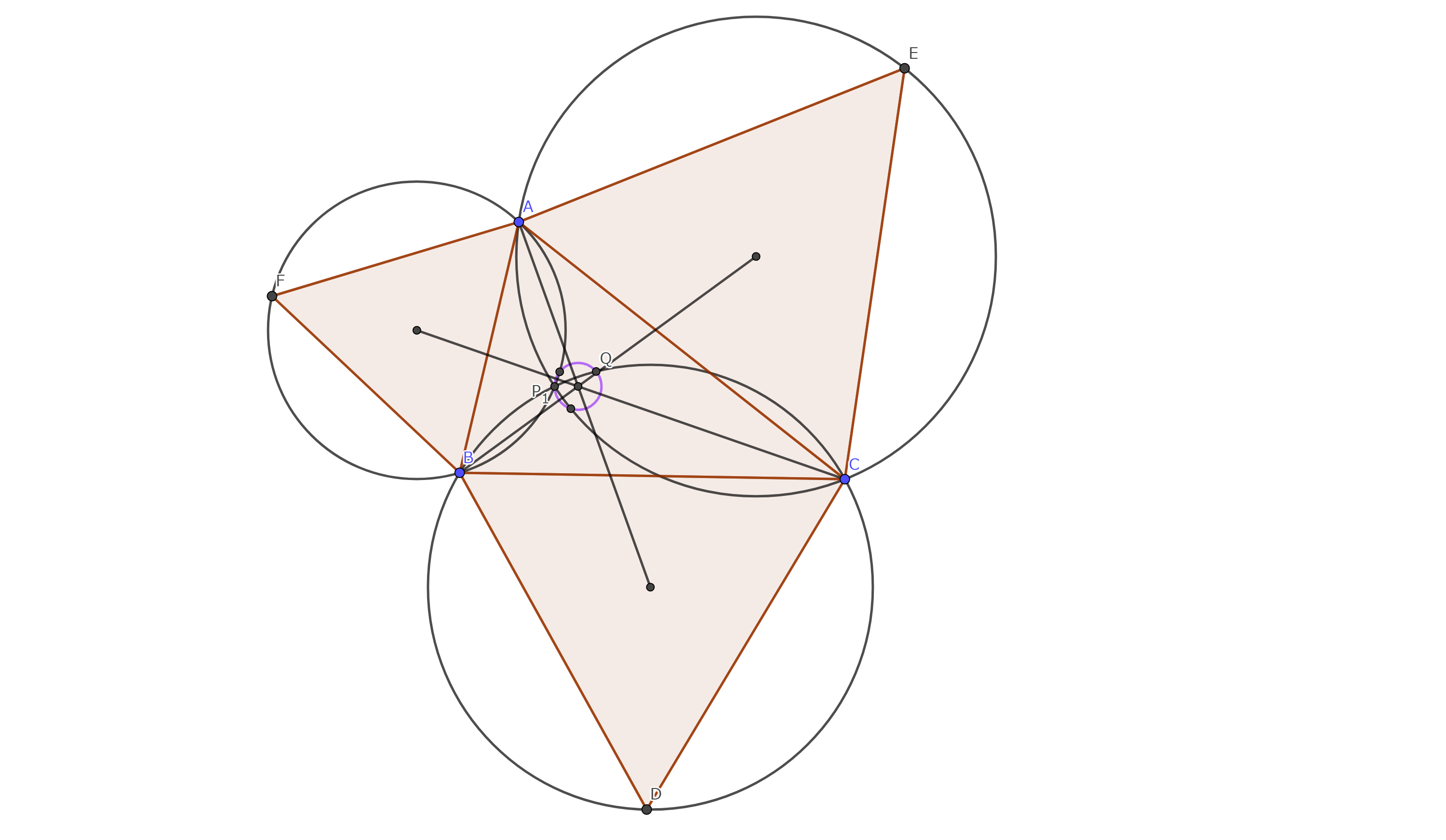
同様にして第二等力点でも証明が可能です。
$\triangle P_{1}'BC,\triangle P_{1}'CA,\triangle P_{1}'AB$のそれぞれの第一フェルマー点をそれぞれ$A',B',C'$とすると
$AA',BB',CC'$は共点である。
終わりに
最後までお読みいただきありがとうございました。
2023/11/28...ナポレオン点の方の命題を追加
2025/03/23...
一般化
を投稿
