数学的帰納法をExcelのシートで説明してみる

数学的帰納法

数日前、数学的帰納法の原理を誤解していると思われる投稿が話題になっていた。
数学的帰納法は、自然数$\mathbb{N}$のすべての要素に対して成り立つ命題を証明するのに使用する。自然数に$0$を含めるときと含めない場合があるが、大した違いではないのでこの記事では含めないとする。
$n\in\mathbb{N}$ （$n$は自然数である）とき
$P(n)$は$n$が含まれる命題やそれが成り立つことを表すとする。
数学的帰納法とは、

という証明の方法である。
論理式で書くと、

だが、誤解していると思われる主張は、
「どんな自然数$k$に対して$P(k) \Longrightarrow P(k+1)$」の部分が、
「ある自然数$k$が存在して$P(k) \Longrightarrow P(k+1)$」になっている、すなわち

となっているものである。
こちらでは
$ \forall n\in \mathbb{N};P(n)$
が成立することは導けない。

有限版の数学的帰納法

これが成り立つことは以下のようにしてわかる。
$P(1)$
$P(1) \land (P(1) \Longrightarrow P(2)) $なので、$P(2)$
$P(2) \land (P(2) \Longrightarrow P(3)) $なので、$P(3)$
$$ \cdots $$
$P(m-1) \land (P(m-1) \Longrightarrow P(m)) $なので、$P(m)$
$P(m) \land (P(m) \Longrightarrow P(m+1)) $なので、$P(m+1)$

$\therefore \forall n\in \lbrace 1,2, \cdots ,m+1 \rbrace;P(n)$∎

表計算ソフトExcelのシートで説明してみる

準備

1. Excelブック（シート）を新規作成
   新規作成
2. セルA1に値「○」を入力する
   ○の入力
3. セルA2にセル参照の数式「=A1」を入力する
   セルA1の値と同じ値が入るようにする数式である。入力モードが終わると、「○」が表示される。
   セル参照の入力
4. セルA2からA5を選択する
   セル範囲の選択
5. キーボード[Ctrl]+[D]を押してA2の数式をA3-A5にもコピーする
   [Ctrl]+[D]は選択している一番上の行の内容を下のセルにもコピーするショートカットである。
   結果、A2-A5には「○」が表示される。
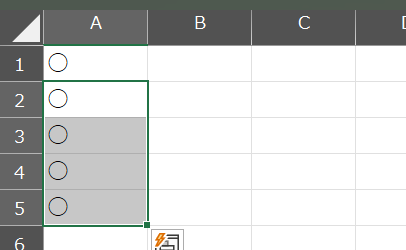   セル参照の結果
6. [Ctrl]+[Shift]+[@]で数式を確認する。
   A1には「○」が入っており、A2-A5にはすぐ上のセルの参照が入っている。
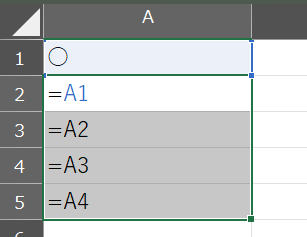   数式の確認
   [Ctrl]+[Shift]+[@]で通常表示に戻る

あえてこの結果を証明する

この状況で、「A1-A5のすべてのセルの値は「○」である」という結果を有限版の数学的帰納法で証明してみる。
セルA1～A5をAを省略してセル1～5と呼ぶことにする。
$P(k)$は「セルkの値は「○」である」という命題が真であることとする。

1. $P(1)$
   手順の2.でセル1に「○」を入力したのだから、「セル1の値は「○」である」が成り立つ。
2. $ \forall k \in \lbrace 1,2,3,4 \rbrace ;(P(k) \Longrightarrow P(k+1))$
   「セルkの値は「○」である」が成り立つと仮定する。（$P(k)$が真、帰納法の仮定）
   セルk+1の値は、すぐ上のセルkの値と同じなのだから帰納法の仮定より、「○」であるので、セルk+1の値は「○」である。つまり$P(k+1)$が真であることが示せた。

（有限版の）数学的帰納法により、
$ \forall n \in \lbrace 1,2,3,4,5 \rbrace ;P(n)$
すべての$ n \in \lbrace 1,2,3,4,5 \rbrace$に対して、「セルnの値は「○」である」
が示せた。∎

$\exists k \in X;(P(k) \Longrightarrow P(k+1)) $ではダメな理由

$\exists k \in X;(P(k) \Longrightarrow P(k+1)) $
（ただし、$X$は $\lbrace 1,2, \cdots ,m \rbrace$もしくは$\mathbb{N}$）
はある$X$の要素$k$が存在して、$P(k) \Longrightarrow P(k+1)$が成り立つなら真となる。
例えば、A1には「○」、A2には「=A1」、A3以降空欄の場合も
$P(1) \land \exists k \in X;(P(k) \Longrightarrow P(k+1)) $は成り立つ
（$\because$ $k=1$の時$P(1)\Longrightarrow P(2)$が成り立つので）
誤った数学的帰納法が正しいのであれば、$\lbrace 1,2, \cdots ,m+1 \rbrace$すべてのセルが「○」となるはずだが、
実際には、A1とA2のみ「○」であとは空欄であるからである。∎
正しい数学的帰納法の記述で$(P(k) \Longrightarrow P(k+1) $の前に来るのは、
$ \exists $ではなく、$ \forall$でなければならない。

終わりに

特に自然数の最初の有限個についての数学的帰納法はとても自明なものであり、便利であるが、もし示すべき個別の命題のどこかが欠けているならば、「命題」が全体で成り立つことの証明に適用できない。
本記事はほぼ自明な内容であるが、自明なことも誰かに説明しようと考えることはそれなりに勉強になると感じた。