数学Ⅰの難問を数学Ⅰだけで鮮やかに解いていく。（解説記事）

この記事について

ハロー（全国全時間帯対応）健全を必要とする人です.
この記事では、 数Ⅰを簡単だと思ってる人への挑戦状 の解答解説を書いています.

ほんへの解答解説

一応この記事から読んだ人がわざわざ前記事に戻らなくていいようにひとつひとつ問題文を再度掲載しておりますので、そのまま読み進めて気まぐれに問題にチャレンジしていただいて結構です.

問題１　対称式と二次方程式

難易度は上から二番目と初っ端胃に優しくない問題でしたが、とにかく$A,B$の値がキショいですよね.
ルート（僕は根号よりルート派です）の中に分母分子ともにルートがある分数が搭載、さらにはその二つをさらに分母と分子に置いた$P$の値を求め、さらにさらに$P^2+ \frac{1}{P^2} $の値の整数部分を求めて.......（つづく）
と、使いたい$a$の値を求めるだけでものすんごい計算量が要求されますが、仕方ないかと思って白目でも剥きながら丁寧に計算していけば$a$の値はまあ出ます.（なんせ数学Ⅰのはじめの単元である『数と式』の内容を詰め込もうと思ったら、これぐらいの計算量になるのは必然だとは思えないですか？）
まず、$\frac{ \sqrt{b} }{ \sqrt{a} }$=$\sqrt{ \frac{b}{a} }$という性質を活かして、$$ P= \frac{A}{B} = \frac{ \sqrt{ \frac{ \sqrt{5}+1 }{ \sqrt{5}+2 } } }{ \sqrt{ \frac{ \sqrt{5}+2 }{ \sqrt{5}+3 } } } = \sqrt{{ \frac{\frac{ \sqrt{5}+1 }{ \sqrt{5}+2 }}{\frac{ \sqrt{5}+2 }{ \sqrt{5}+3 }} } } $$
両辺に($\sqrt{5}+2$)($\sqrt{5}+3$)をかけて、
$$P= \sqrt{ \frac{( \sqrt{5}+1 )( \sqrt{5}+3 )}{ ( \sqrt{5}+2 )^{2} } } $$
これを整理すると、$P= 2\sqrt{ \sqrt{5}-2 } $となります.（わあ簡潔）
使うのは$P^2$と$ \frac{1}{P^2} $ですから、それぞれ$P^2=4( \sqrt{5}-2 )$,$\frac{1}{P^2}= \frac{1}{4( \sqrt{5}-2 )} $となる.
よって、$P^2+\frac{1}{P^2}=\frac{16( \sqrt{5}-2 )^2+1}{4( \sqrt{5}-2 )}$
したがって、整理すると、
$$P^2+\frac{1}{P^2}= \frac{17 \sqrt{5}-30 }{4} $$
問題文には$\sqrt{5}=2.236$を使ってもいいと書いているので、$(17×2.236-30)÷4=8.012÷4=2.003$
ってことで、整数部分$a$は$2$！！（ようやく本題に入れます）
与式に$a=2$を代入すると、$y^2(2y^2-2x- \frac{6}{2})+x(x+2y-2)+2=0$
$⇔2y^4-2xy^2-3y^2+x^2+2xy-2x+2=0$
$x$の方が次数が低いですから、$x$について整理すると、
$x^2-2(y^2-y+1)x+(2y^4-3y^2+2)=0$
これを満たす実数$x,y$が存在する、ということですから、$f(x)=x^2-2(y^2-y+1)x+(2y^4-3y^2+2)$とすると、$f(x)$が$x$軸と共有点を持つ、つまり$x$が異なる実数解を$2$つもつときと、$x$が重解をもつときの二通りあるということですから、この二次方程式の判別式を$D$とすると、これを満たす条件は$D≧0$です.
ここで、$D/4=(y^2-y+1)^2-(2y^4-3y^2+2)≧0$
$⇔(y^4+y^2+1-2y^3-2y+2y^2)-2y^4+3y^2-2≧0$
$⇔-y^4-2y^3+6y^2-2y-1≧0$
$⇔\boldsymbol{y^4+2y^3-6y^2+2y+1≦0}$

「お、四次式じゃ～ん.んじゃ因数定理」なんてならないでくださいね. 今回の問題の趣旨は「数学Ⅰまでの範囲で解ける問題」ですから、勿論ここも数学Ⅰの範囲で解くことができます.
ズバリその方法は次数下げでございます.
次数を下げるということは、文字で割るということですが、このとき注意しなければいけないのは、割ったときに、文字$≦0$であるか否かですが、これをラクラクと解決するのが、二乗のカタチで割ることです.
たぁだー！文字が$0$になる場合を省いてです.
$y=0$のときは、$0^4+2・0^3-6・0^2+2・0+1≦0$
$⇔1≦0$なのでこれは解として適していませんね.
次に、$y≠0$のとき、$y^2$で両辺を割ると、
$y^2+2y-6+ \frac{2}{y}+ \frac{1}{y^2}≦0 $
この式を見て因数分解できそうと思った人は因数分解の練習をしっかり積んできた人だと思います.
もうすこしヒントを与えます.
$y^2+ \frac{1}{y^2} +2(y+ \frac{1}{y} )-6≦0$
お分かりでしょうか？これは相反方程式と言ってこのように変形できます.
$(y+ \frac{1}{y} )^2-2+2(y+\frac{1}{y})-6≦0$
$⇔(y+ \frac{1}{y} )^2+2(y+\frac{1}{y})-8≦0$
$⇔(y+ \frac{1}{y}+4)(y+ \frac{1}{y}-2)≦0$
$⇔-4≦y+ \frac{1}{y}≦2$
これを$y+ \frac{1}{y}$のまま数学Ⅰの範囲で解くなら$y$でかけて、$y$が正か負かの二通りの場合分けから答えを出すこともできますが、ここではまた少し変わったやり方を紹介しておきます.
ズバリその方法は$t$置換でございます。（take2)
$y+ \frac{1}{y}=t$とおきます.
この式に、$y$をかけると、$y^2+1=ty $
$⇔y^2-ty+1=0$
解の公式より、$y= \frac{t± \sqrt{t^2-4} }{2} $
$-4≦t≦2$ですから、$t$の最小値は$-4$
よって、$y$の最小値も$t=-4$のときですから、
$y=\frac{-4± \sqrt{(-4)^2-4} }{2}$
したがって、$y=\frac{-4± \sqrt{12} }{2} =\frac{-4± 2\sqrt{3} }{2}=-2±\sqrt{3}$
よって小さい方を取って、$y$のとりうる最小値は$y=-2-\sqrt{3}$
最後はまあ見慣れない解法だったとは思いますが、$t$置換する前の場合分けを考えれば、計算はこちらの方が幾分かマシになると思います. ぜひ頭の片隅にでもこの知識を入れておいていただけたらなと思って、今回はこの解き方をしてみました.

問題2　条件いっぱい命題と論証

難しいね　難しいサ　難しいかな　難しいかも　難しそう　難しいから　難しいとも　難しいと言ってるから　難しいからこそ　命題ッ！　論証ッ！（某アニメキャラクター）
ってことで魔女kkじゃなくて条件いっぱい命題と論証を討伐していきます.（某アニメを知らない人はちょっとなに言ってんだかわかんない（サンドイッチマン風）てな感じだと思いますが、彼はこういう人です. こういう人が作ったこういう記事だと思って読んでいってください）
で、本題の(1)に入るんですが、その前にみなさんは①,②,③を見てなんとも思わなかったですか？体が疼かなかったですか？思ってほしいし、疼いてほしいです. ついでに$1$万円もほしいです.
つまりなにが言いたいかと言うと、①,②はどっちも$c$という同じ範囲を持っていますから、合体できそうですよね. ③は因数分解できそうですよね
実際できますから、まずそれをしていきましょうか.（これが後々役に立つことを彼はこのとき知る由もなかった....）
①,②を合体するとき、符号はどっちに合わせようかな？とか今日のファッションは全身タイツにしようかな？なんてことは考えなくていいです. 符号は②が$c$より小さいということなので、②の符号に合わせましょう.
したがって、$ax+by>bx+ay$
よって、$(a-b)(x-y)>0$
この不等式の解は、$a>b$かつ$x>y$、または$a< b$かつ$x< y$という解になります.（この解の書き方が正しいのかは自信が無いです）
次に③を因数分解します. もうたぶんみりゃわかると思うので因数分解したら、$(a-b)(x-y)=0$
つまり、この方程式の解は、$a=b$または$x=y$という解になります.
東西南北上下左右$360°$どっから見ても、明らかに①,②を合わせた範囲と③が別モンというのがわかりますね.（集合的に言うなら排反ってヤツ）
よし. じゃあこれを踏まえて、(1)を解いていきましょう！
えーと？...(1)の問題文は、①,②,③を同時に満たす$a,b$および$x,y$が存在しない.....え！！これさっきもう示したも同然じゃん！！！
てことではい. これを模範解答風にすると以下のようになります.

まあ、(1)はそれほど難しくはなかったかなーとも思いますが、問題作った側は元々答え知ってて作ってるから、あんま当てになんないっすね.
こういう条件がたくさんある問題って、どこから攻めればいいんだろう？みたいなことが多々出てくると思うんですが、まず方針を立てることは忘れてはいけないですね. 今回の場合は、似たモン同士くっつけて、むしゃくしゃする形の式をすっきりした形に直して...とまず土台をしっかりすることから始めたらそれが答えにつながった. みたいな問題だったんですけど、これからはきっちりと方針を立てて進めていかなければならない問題（次の問題）がわんさか出てきますから、問題文が意味わからんって思ったら分かったところから始めて徐々に問題の見通しをよくしていくことが....(2)で役立ちます！！方針を立てるというスキルを習得したので速攻(2)を殺りましょう！！

ごちゃごちゃしてて吐き気を催しますね. まず動きまくる区間を捉えるのがくそ面倒で、その上同時に満たす条件が四つもあるのですから、どっから攻めればいいか、方針を立てづらいです.
しかしこの問題、瞬殺することができるんです.
分かることから攻めるのが大事と先ほど言いましたが、問題文から分かることは何でしょうか？
大体みなさんがすぐわかるだろうことは、④からは$c≧0$、⑤からは$xy≧0$ということ.
あと他なんでしょう. そろそろ読むのやめようかな.とかですか？あ、いやそんなこと分かってはいけませんよ. 他は、意外と見落としそうな$x=0$が必ず区間内に入ること、でしょうか.
先に言いますが、これはこの問題においてくっそ重要です. (2)RTAをしようと思ったらかかせない考え方なんですが、$x=0$のとき、他の値はどうなるんでしょうか.
まず⑤から、$x=0$のとき、$|0-y|=0・y$
これを満たす実数$y$は$y=0$しかありません.
そしたら、①,②に$x=0,y=0$を代入すると....？
なんとなんと、①から$a・0+b・0≧c$
　　　　　　　②から$b・0+a・0< c$が得られます.
つまり、$0≧c$であり、$0< c$であるということですが、そんな実数$c$はこの世に存在しません. トリコの最終回「暴走したトリコを小松が泣きながら調理して食べる」なんてのと同じくこの世に存在しません.トリコの最終回はトリkk(自主規制)
$c$が存在しなければ$a,b$も存在しないので命題は真. というわけです.
いやーんなにこれすごい簡単じゃな～いって思った人いますよね. そうなんです. すげー簡単なんです、これ. でも、難しい. なんででしょうか？それは解けなかった（前提）あなたの心に聞いてみてください.
存在するか否かというハムレットみたいな命題をみると、直接法か背理法、対偶か、なにで解いてこうかなみたいなのを考えるまでもなく解ける問題でしたので、そういう癖がついてる人には逆に度肝を抜かれるような問題だったかなと個人的に考えてます.
いつも思うんですけど、解答見たら「これ絶対簡単な問題やなー（笑）」みたいに思っていざ答え知らずに解いたら難しいみたいな問題（順序逆だな）っていっぱいありますよね. これもそのひとつだったと思ってます.
最高難度の癖してすぐ終わっちゃって味気ないですが、発想と問題文の解釈が難しいと感じるかなと思って最高難度にしました.
基本はめんどくさいから模範解答を書かない方針で行きますが、書いてほしければ言っていただけると模範解答も付しますのでどうぞご遠慮なさらず.
次！！

$EX$. 条件いっぱい命題と論証 and 関数

(1)は既視感がありますね. (2)はもう完全に関数の問題文ですね.
今回の問題の方針はどうしましょうか. とりあえず、水鉄砲を買う⇒覆面を被る⇒コンビニ強盗⇒潔く捕まる、という方針にしますか？したくありませんね. この問題では、前問の(2)での方針のような$x=0$を使った解き方はあまり有効ではなさそうです. じゃあほかの方針を立てる必要がありますが、今回の問題の方針としては、まず(1)では、$f(x)≧0, g(x)<0$がまとめられそうです. あと前の問題の(1)から、①,②を同時に満たすときは$a>b$かつ$x>y$、または$a< b$かつ$x< y$が成り立つということですね.
分かるのは大体これぐらいしかないですね.
とりあえず、$f(x)$と$g(x)$をまとめて、$f(x)>g(x)$として、これから$F(x)=f(x)-g(x)$とすると、$F(x)>0$が成り立つことを前提とすればいいわけです.
\begin{eqnarray} F(x) &=& f(x)-g(x) \\ &=& (ax^2+by+c)-(bx^2+cx+a) \\ &=& (a-b)x^2+(b-c)x^2+(c-a) \end{eqnarray}

見てすぐビビビッって因数分解できるとわかってこれをすぐ因数分解しようとする人もいるかもしれませんが、ちょっと落ち着きましょう. ほら温かいお茶でも飲みながらゆっくりと......してる時間はあるかどうかはわかりませんが、お茶を飲みながらでも読んでください. 今回は因数分解してなにか恩恵が受けられそうですか？しても多分前問の(1)のように矛盾を示せるわけでもないし、因数分解から解を出そうと思ってもけっこう面倒です.（因数分解すると、$ \frac{c-a}{a-b} と1$の大小を比較して解を出す必要がある）
そもそもとして今回はさほど解は必要ではないんですよね. 求めたいものはなんでしたか？ちょっと曖昧ですが、不定の区間内で$F(x)>0$が成り立つうえで①,②を満たす実数$a,b,c$があるかないかということでした. ①,②は$a,b$と$x,y$の大小関係を示しているものと分かっているので、ここからしていくのはどうにかして$a$や$b$が入った範囲を求める、この作業に重心を置きましょう. 因数分解して出した不等式の解から範囲を求めるより、簡単な範囲の求め方――そう. それこそ半沢直樹.....あ、違った. それこそ判別式なのです.....！！
判別式から得られる恩恵はありがたいと思えるでしょうか？いまいち思えない人は「STEINS GATE」をプレイするか視聴するかしてありがたみを知ってきてください. いやこれじゃ分かんねえか. ゲームとアニメで分かる世の中のありがたみってのは「日本に生まれたこと」ぐらいでしょうからね.（個人の感想）
で、判別式の恩恵に関してなんですが、まず判別式は文字を減らすことができるのが特徴的ですね. 今回は$a,b,c$について議論していきたいのに、出しゃばりの$x$君がいてこのままだと答えを示しづらいですが、そのときは判別式という刃物で$x$君をギッタギタのめった刺しにしてやって消滅させます. 大丈夫です. 数学界の憲法には判別式で文字を殺しても罪に問われないと定められてますから.
あとはまあネット検察すると（おい）解の個数を楽々と調べられて、視覚的にグラフをイメージできるから.....みたいな恩恵もありますが、今回ありがたく使わせていただく恩恵は$a,b,c$の範囲決めぐらいです.
ではまず定型文を添えてあげます.（断りも含む）
$a≠b$であるから二次方程式$(a-b)x^2+(b-c)x^2+(c-a)=0$ の判別式を$D$とすると、$F(x)>0$となる条件は、$a>b$かつ$D<0$であること.
一応確認しますが、ここまでで言わなかった$a≠b$やら$a>b$やらは理解できますね？$a≠b$でないといけない理由は、$a=b$のときは、$x^2$の係数が$0$になってただの一次関数に成り下がってしまう（次数が高いほど位が高いとは限らないよな）ので、そうならないように$a≠b$と初めに断っておいて、$a≠b$を断るなら通常その場合も考慮しなくてはいけないのですが、今回は③の条件式を満たさないので、$a≠b$であるということでごわす. んで、特にこれを断って矛盾が生じることもなさそうなので続きを書いていきます.
$D=(b-c)^2-4(a-b)(c-a)<0$
めんどいから計算過程省略して$b$について整理すると、
$b^2-2(2a-c)b+(2a-c)^2<0$
でここでこそ見てすぐビビビッってなって因数分解してほしいところなんですけど、実際に因数分解してみると以下のようになります.
したがって、$ \lbrace b-(2a-c)\rbrace ^2<0$
もうお分かりですね？$a,b,c,$は実数であることより、$\lbrace b-(2a-c)\rbrace ^2≧0$
つまり、$F(x)>0$となる実数$a,b,c$が そもそも存在しないんです！$F(x)>0$となる実数$a,b,c$が そもそも存在しないんです！（さほど大事なことではないがなんとなく二回言った）
てことでこれで命題は真というのが示されたわけですけど、いまいち消化できない人もいるんじゃないですか？だって、前提である$F(x)>0$（元の命題の文では違います）がそもそも成り立たなかったから、①,②を同時に満たすも満たさないもくそもへちまも福沢諭吉もありませんからね. だからこれは僕の「気持ち悪い問題作成魂」によってつけられたただの飾りだったわけです. なくても問題としては全然成立したんですが、最初の①～⑤の条件式を使ってますよってアピールと問題文をややこしくするために①,②を同時に満たす、という文言を付け加えました.（性格良すぎ）
ただ元々示したかったのは「実数$a,b,c$が存在するかしないか」だったので、意には沿ってますよね. だって、今回の$F(x)>0$は$a,b,c$が実数だったから成り立たなかっただけであって、これが虚数だったとしたら$F(x)>0$は成り立ちますよね. だからまあ、消化できないとしたら①,②を同時に満たす、っていう文言についてだと思いますが、これは僕の性格の良さ()のせいで生まれた副産物ということでどうにか腸まで届かせてトイレに流してください.
では続きましては(2)です.まず、「区間 $\frac{1}{2}< x<3$ のすべての実数 $x$ に対して $f(x)< g(x)< h(x)$を満たす任意の整数 $a,b,c$について、④が常に成り立つか判定せよ.」を読み取っていきたいんですが、みなさんは思わなかったですか？「区間$ \frac{1}{2} < x<3 $のすべての実数$x$に対して」って、ぜってぇ反例出てくるっしょ～、って. ああ思わなかったんですか. 思わなかったなら仕方ないですね. 目の前の電子機器を三発本気で殴りましょう. そしたら思えるようになります.
英語の先生に「長文の適当文を選択する問題で『all(すべて)』とか『only(たった～だけ)』みたいな極端な文字がある文はほとんど不適当」って言われてから、英語だけでなく他の事にも言えると思って、数学だと「すべての実数$x$は～」とか、憲法の「すべて国民は～」は間違ってること、と思ってから考えるようになった僕（※彼は冗談を言っています）は命題文を考えた後「これ絶対偽やなー（笑）」って思ってから解き始めました. こういう先入観が逆に功を奏することもあります. その例としてまずは正攻法、じゃない解き方を紹介します.

これ見てどう思いましたか？「お前答え知ってるからこんな解答方法が思いついたんだろ！」って思った人、まあ多分絶対（どれ？）いますよね. そうじゃないと証明する術がないので言及しませんが、これを思いつくのは別に問題を作った僕だからでは決してありません.問題を解く側の人も考えようと思えば考えられます. その理由は$f(x),g(x),h(x)$の値が$a,b,c$を循環させているだけで、区間内に$\boldsymbol{x=1}$が含まれているのさえ確認できればこれを思いつくのは容易です. あと、さっき言った先入観「すべての実数$x$に対して～」って文に、ん？ってなればもっと考えやすくなると思います. 個人的に、（てか多分他にも結構いると思うが）$x$とか$a$の値に関する命題の真偽は$0,1,-1$は意外と刺さると思います. これは命題の反例探しのコツとでも思ってください.
では、目の前の電子機器を三発本気で殴った方々がた・ぶ・んしたであろう正攻法を紹介して次の問題に移りませう.

問題3　絶対値つき二変数関数

この前の三問ですでに二次関数の内容はちらほら出てきましたが、この問題は完全なる二次関数の問題となっております. 多分この問題は比較的取り組みやすかったとは思いますが、それでも絶対値がいることで場合分けが発生するという点では面倒というのは変わりないですね.

ところで、まずこの問題の解説に入る前に僕が参考にした入試問題を二問（というよりパクった）紹介、模範解答を提示してから本題に映ります.

ああ長い！！！

入試問題から引っ張ってきましたから、まあまあの難易度だったとは思うんですが、それでもまだどちらも「あーなるほど. まあいけるね」みたいな人も多いんじゃないですか？僕もそうでしたよ. まだそんなむずくないなぁと感じました。そこで僕が閃いたのが問題3「絶対値つき二変数関数」というわけです. もう一度問題を眺めてみましょう. 小一時間ほど眺めてみましょう。

...（小一時間後）さあどうですか？なんか確かにさっきの二問がミックスされたみたいな形の問題文に見えますよね？ね？何が見えてきましたか？え？あなたのかっこいい顔だって？またまたお世辞がお上手なんですから～. 僕の顔よりジョン万次郎の顔の方が全然かっこいいですよ～. まあジョン万次郎（気になる方は検索）は置いておいて、見えてきたのは、二つの場合分けと、絶対値を外した式が二次式となり、$x+2y=t$とおいて解かなくてはいけない、という解法でしょう.（知らんけど）じゃあ、もうほとんどさっきの二問とほとんど解き方が同じになってあんま面白味がないので、解き方が違うところだけ解説して、あとは機械的に処理していきましょうか.

まず、$x|2x+y|+y|x-2y|=2$・・・①、$x+2y=t$とおきます.
また①については、二つの場合分けが考えられます.
［１］$x-2y≧0$のとき、と［２］$x-2y<0$のときの二つです.
なんで$2x+y$は正か負か考えないの？っていう理由は単純で、実数$x,y$は$x≧0,y≧0$だからプラスで繋がれて愛を育んでいる$2x+y$は必ず正になるから、というわけです. だから例題1と違って、場合分けは二つで済むわけですね.
じゃあ［１］$x-2y≧0$のときから行きましょう.
例題の如く$x+2y=t$を$x=t-2y$と変形して、①に代入.
①は、$x(2x+y)+y(x-2y)=2$となり、整理すると、$$ x^2+xy-y^2=1 ・・・②$$
知ってる人は知ってると思いますがこの式はいわゆる"双曲線"というやつですね. 後ほどグラフを貼りだします.
②に$x=t-2y$を代入します。
したがって、$(t-2y)^2+(t-2y)y-y^2=1$
$⇔y^2-3ty+t^2-1=0$
うしうしじゃああとは例題2みたいに判別式$D$を使ってちょちょいのちょいだな.ああ楽勝だぜベイベー.（フラグ）
この二次方程式の判別式を$D₁$とすると、$y$が実数解をもつための条件は$D₁≧0$
$D₁=(3t)^2-4(t^2-1)=5t^2+4≧0$
・・・あれ？これ実数$t$がどんな値でも成り立つよな？
いやでも例題2は判別式使って解いてたし、普通はこれで答えが出せるはずなのに....ど、どうしよう～💦💦答えが出せないよ～😭ーーーBAD ENDーーー
ってなるわけないですね. させませんそんな〇しの子みたいなカスエンドは. ではどうやって答えを導いていけばいいんでしょうか？
試しに判別式が死んだ後にビンタでもしてやりましょうか.
そんなんしちゃだめですよ.亡者には敬意を払うのが普通ですから.
で、ここからの答えの導き方はこれまた見慣れない人もいるかもしれませんが、またもや解の公式のご後輪です.あじゃなくてご降臨です.
某学習通信アプリの某有名数学教師が「解の公式なんて使うんじゃない」って言ってた記憶があるんですが、（実際そうです。解の公式は最終手段ですので初っ端使おうとする人は死んだ後ビンタされたほうがいいです）解の公式は最初の問題1でも使ったようにただ因数分解できない二次方程式の$x$の値を求めるためだけの道具ではないんですよね.
その存在証明をここで示してみせます.
②の解は、解の公式より、$y= \frac{3t± \sqrt{5t^2+4} }{2} $と分かりますが、［１］で生じた範囲$x-2y≧0$に注意して$y$の解を絞り込みます.
$x=t-2y$ですから、この不等式は
$(t-2y)-2y≧0⇔y≦ \frac{1}{4}t $
このとき、大きい方の$y$の解は、明らかに$t≧0$ なら$ \frac{3t+ \sqrt{5t^2+4} }{2}> \frac{1}{4}t $なので、ここで$y$の解は$y= \frac{3t- \sqrt{5t^2+4} }{2} $のひとつに絞られた.
また、$y≧0$でしたので$\frac{3t- \sqrt{5t^2+4} }{2}≧0 $
$⇔3t≧\sqrt{5t^2+4}$
$⇔9t^2≧(5t^2+4)$
$⇔4t^2≧4$
$t≧0$だから、$t≧1$が不等式の解です.
そして、$y≦ \frac{1}{4}t $の不等式も満たすか確認する必要があります.
$\frac{3t- \sqrt{5t^2+4} }{2}≦\frac{1}{4}t $
$⇔2(3t- \sqrt{5t^2+4} )≦t$
$⇔5t≦2\sqrt{5t^2+4}$
$⇔25t^2≦4(5t^2+4)$
$⇔5t^2≦16$　したがって、$t≧0$より、$t≦ \frac{4}{ \sqrt{5} } $
よって、［１］での$t$の範囲は、$1≦t≦\frac{4}{ \sqrt{5} } $
次に［２］での$t$の範囲を求めていきますが、ここからは例題2と同じ感じなので、機械的に行きます.
［２］$x-2y<0$のとき、$x(2x+y)-y(x-2y)=2$
したがって、$x^2+y^2=1$（原点を通る半径1の円なんて僕は知りません）
この式に、$x=t-2y$を代入して、$(t-2y)^2+y^2=1$
したがって、$$ 5y^2-4ty+t^2-1=0・・・③$$
この二次方程式の判別式を$D₂$とすると、$y$が実数解をもつための条件は$D₂≧0$
よって、$D/4=(2t)^2-5(t^2-1)=-t^2+5≧0$
すなわち、$t^2-5≦0⇔- \sqrt{5}≦t≦\sqrt{5} $となり、$t≧0$より、$0≦t≦\sqrt{5} $
また、このとき、$x<2y$を満たすかどうか考えなければならない.
$x=t-2y$から、$x<2y⇔t-2y<2y⇔t<4y⇔y> \frac{1}{4}t $
ここで、③の解の公式より、$y= \frac{2t± \sqrt{5-t^2} }{5} $
（ちなみに$x<2y$を調べることは同時に、$y≧0$を調べていることになる。$x≧0$を調べないのは、$y≧0$を調べるのと結局同じ結果になるから、$t$と$y$に依存する$x$の値より$y$の値を直接求めよう.という魂胆である）
よって、$\frac{2t± \sqrt{5-t^2} }{5}> \frac{1}{4}t $
$⇔4(2t± \sqrt{5-t^2})>5t$　
$⇔3t>± 4\sqrt{5-t^2}$
$⇔9t^2>16(5-t^2)$
$⇔25t^2>80$　したがって、$t> \frac{4}{ \sqrt{5} } $
よって、［２］では$t$の範囲は$\frac{4}{ \sqrt{5} }< t≦\sqrt{5} $
［１］の範囲と合わせて、$1≦t≦\sqrt{5}$
$t=1$のとき、$y^2-3・1・y+1^2-1=0$
$⇔y^2-3y=0$　よって、$y(y-3)=0$より、$y=0,3$
$y≦ \frac{1}{4}t $すなわち、$y≦\frac{1}{4}$を満たすのは、$y=0$のみ. このとき、$x=1-2・0=1$
したがって、$x+2y$は$x=1,y=0$のとき最小値$1$をとる.
$t=\sqrt{5}$のとき、$D=0$で③の二次方程式は重解をもつから$y= -\frac{-2t}{5}=\frac{2\sqrt{5}}{5} $
したがって、$x=t-2y=\sqrt{5}-2・\frac{2\sqrt{5}}{5}=\frac{\sqrt{5}}{5}$　これは$x-2y<0$を満たしている.

よって、$x+2y$は$x=\frac{\sqrt{5}}{5},y= \frac{2\sqrt{5}}{5}$のとき最大値$\sqrt{5} $をとる。
ゆえに、$x+2y$は$x=1,y=0$のとき最小値$1$
　　　　$x=\frac{\sqrt{5}}{5},y= \frac{2\sqrt{5}}{5}$のとき最大値$\sqrt{5} $

まあ難易度☆三つにふさわしい問題だったでしょうね.
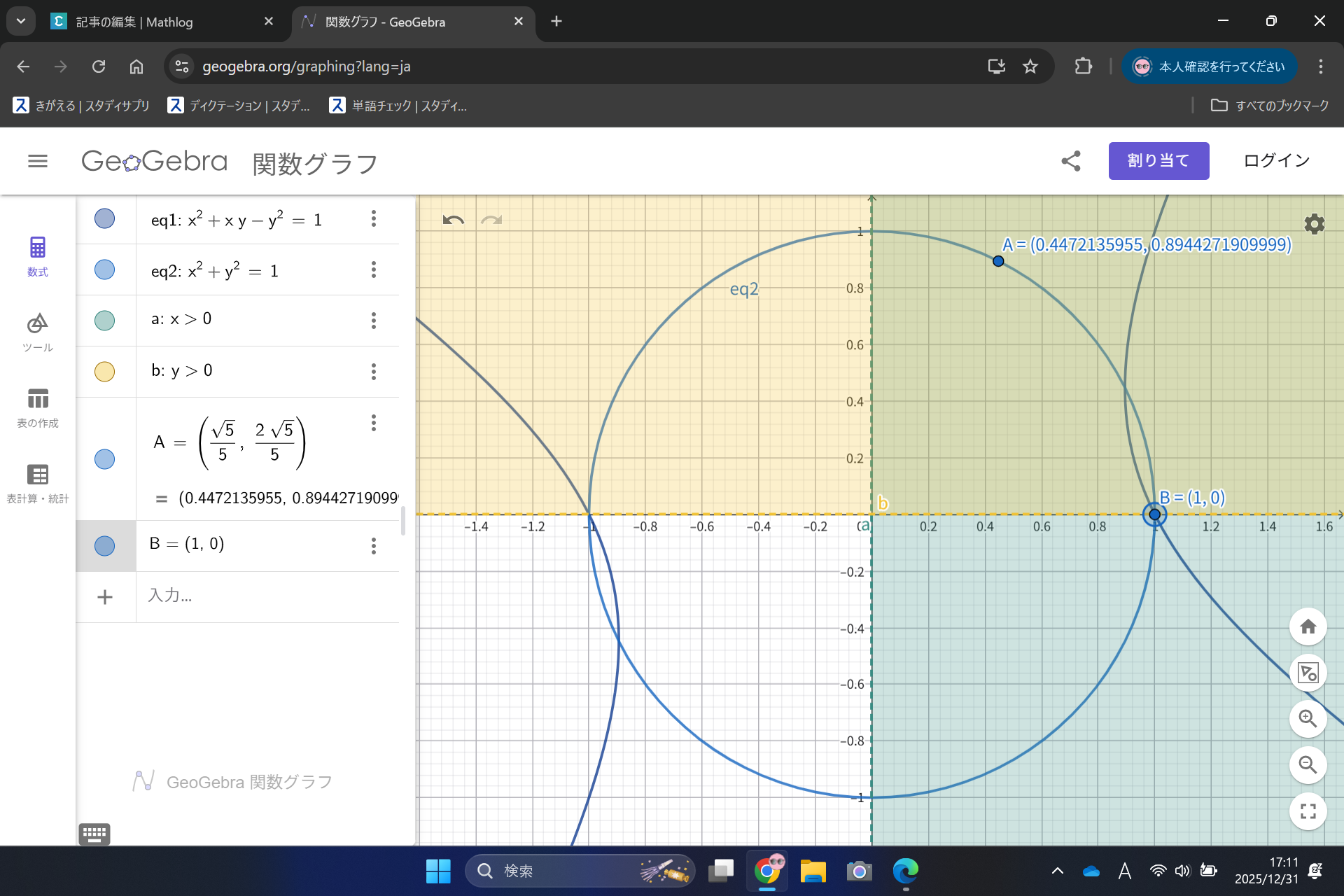
で、解答の途中にちらっとこの絶対値の付いた式（②,③の式）のグラフを提示するといったのでそれを見てみましょう. 出でよ役所広司！！
横浜フランス映画祭 2024 ラインアップ発表記者会見
ああ召喚する者を間違えてしまいました. こっちですね.
GeoGebraで普通に写真を保存する方法あったら教えてください.
なにか分かりましたか？そうです. 役所広司さんの目がキラキラしていることですよね！ですがそれもそうなのですが、グラフの方を見ていただくと、この問題の最大値の$x,y$の値は点$A$の$x$座標$,y$座標で、最小値は点$B$の$x$座標$,y$座標というのが見てわかると思います. 上に記した解き方は判別式や条件の範囲から絞っていく、というような結構面倒な解き方だったでしょう.しかし、この問題実は、このグラフについて考えていくだけで、あまり計算もややこしくない解き方が存在します. 一応数学Ⅱの範囲を多少含む（円の方程式を知ってないと無理なので. 双曲線の方程式も知ってたら役に立つ）のですが、$8$割ぐらいは数学Ⅰ、というか中学範囲みたいなもんなのでご紹介します.

まず、最初は同じく$x+2y$を文字に置き換えます. 気分転換に$x+2y=獄$とおきましょうか.(?) これは$y$の関数と見ると、$y= -\frac{1}{2}x+ \frac{獄}{2} $なので、傾きが$-\frac{1}{2}$ で$y$切片が$\frac{獄}{2}$ であることがわかります. また、絶対値を上と同じように外すと、$x^2+xy-y^2=1$と$x^2+y^2=1$が出てきますね.
まず最小値を見つけ出していきたいのですが、もういちど$x+2y$を見てみると、$x$が小さいより$y$が小さくなる方がより小さい値になりそうですよね. 求めたいのは結局$獄$の最小値ですから、$y$切片$\frac{獄}{2} $ができる限りで小さくなれるときを考えても変わりありません.
じゃあそのときはもちろん$\frac{獄}{2} $が原点に近づいていけばいくほどその値は小さくなっていきますが、ここで条件$x≧0,y≧0,$は必ず満たし 条件$x^2+xy-y^2=1,x^2+y^2=1$はどちらかが満たされていればいいので、言い換えれば、領域$x≧0,y≧0$内で直線$y= -\frac{1}{2}x+ \frac{獄}{2} $が$x^2+xy-y^2=1$または$x^2+y^2=1$のどちらかと交点をもち、かつ$\frac{獄}{2}$ が一番小さいのが求めたい$x+2y$の最小値てなワケです.
つーまーり？限界まで小さくしてどちらかのグラフと交点をもつような$\frac{獄}{2}$は徐々に$y$座標が下がっていき、同時に$x$座標が大きくなりますが、その限界が$y≧0$の境界点の$y=0$というワケです.
このときが限界まで下げた$\frac{獄}{2}$の最小値になるから、$x=1,y=0$のとき最小値$x+2y$は$1$
（ちょっと説明が同じことを繰り返しているように見えて申し訳ないですが、自分自身数学が苦手なのもありますのでご容赦ください.不明な点があったら優しく指摘してクレオパトラ）
次に最大値ですが、自分の中でこの解き方は相当革命的だと自負してます.
まず、$x^2+xy-y^2=1$が双曲線と分かっている人は「双曲線の方がでけえ値とれそうだな」と思えますが、分からない人はまず常識ともいえる$x^2+y^2=1$が原点を通る半径1の円から攻めていくしかないですね.でも、今回の場合、知ってる知らない以前に絶対値を外した時の条件として双曲線のときは$x≧2y$が課されていますから、$y$をでかくして、$\frac{獄}{2}$がでかくなるなという予想も簡単に砕かれますから、しぶしぶ円の方に集中してあげましょう.
じゃあ、円$x^2+y^2=1$と直線$y= -\frac{1}{2}x+ \frac{獄}{2} $に注目するとして、$\frac{獄}{2}$ が一番大きくなるのはどのときかなと考えたら、それが直線$y= -\frac{1}{2}x+ \frac{獄}{2} $が円$x^2+y^2=1$の接線となるときだというのはわかるでしょうか？少し下げると$\frac{獄}{2}$ は小さくなるし、少し上げるとそもそも円と交わりません。つまり、このときが最大値です.
で、ここからが今回の解き方の一番の魅力で、いろんなやり方があると思いますが、僕が知る限り一番計算がラクな方法は「円と接線の性質」を使った、「円の接線は、その接点を通る半径に垂直」というのを活用します.
ある直線に対する垂直な直線の求め方は覚えてますか？覚えてますよね. これは生まれた瞬間に習得できる公式ですからね.ちなみに僕は中三の後半ぐらいに初めて知りました.（←？）
逆数にして$-1$をかけるんでしたね. つまりこの場合接線に垂直な直線は$y=2x$となるわけですね.
で、この直線と円との交点が最大値になる$x,y$の値ですから、
$x^2+y^2=1⇔x^2+(2x)^2=1⇔x=±\frac{\sqrt{5}}{5}$
$x≧0$を満たすのは、$x=\frac{\sqrt{5}}{5}$と、簡単に求められちゃいます！710びっくり平城京ですね！！
あとは芋ずる式に$y$と$x+2y$の値も求まるってぇワケです.
あんな長かった計算式がちゃんと書いたとしても10行ぐらいに！

これも「はえーそんな解き方あったんか」ぐらいで頭の隅に入れておいていただけるとありがたいです.
おっしゃああ次！！！

問題4　美しい比で考える複雑な比

みんな大好き黄金比、といえばかの有名な神々しいパルテノン神殿　比で作り出す問題は好奇心と向上心で難問に仕上げてけよHEY Yo boy　2025は45の二乗で良いお年 2026もまじ超調子良いから数学楽しんでこうよ We are 創造神
ということで気を取り直して最終大問の問題4の解答解説していくんですが、まあ【ア】～【ウ】までは流れ作業みたいなもんすよね. 自分の物差ししか持ってないのでわかりませんが、多分【エ】～【カ】もそこまで難しくないと思います. ちなみに余談ですが、【エ】～【カ】の問題文をどうやって書くかはめっさ悩みました.悩みぬいた結果、この文が一番伝わりやすいかなと思ってこの問題文にしましたが、もしこう書いた方がいいよとかあれば気軽にコメントかテレパシーを送ってください.テレパシーの場合、僕が今住んでいるのがエクアドル（大嘘）なので、受信範囲は南アメリカの中までです. それ以上海外はちょっと......
ではもういちど気を取り直してまずは【ア】からいきましょうか.
勘のいい人は$∠A=72^{\circ},∠A’=36^{\circ}$を見た瞬間、「正五角形の中心角と$\frac{\phi}{2}$（$cos36^{\circ} $）かえ？」って天竜人みたいに言うんじゃないでしょうか？実際題名にある通り黄金比$\phi$を使って解いていきます.
問題を読み進めていくと、まず【ア】はつまりどういうことかと言うと、こういうことです.↓
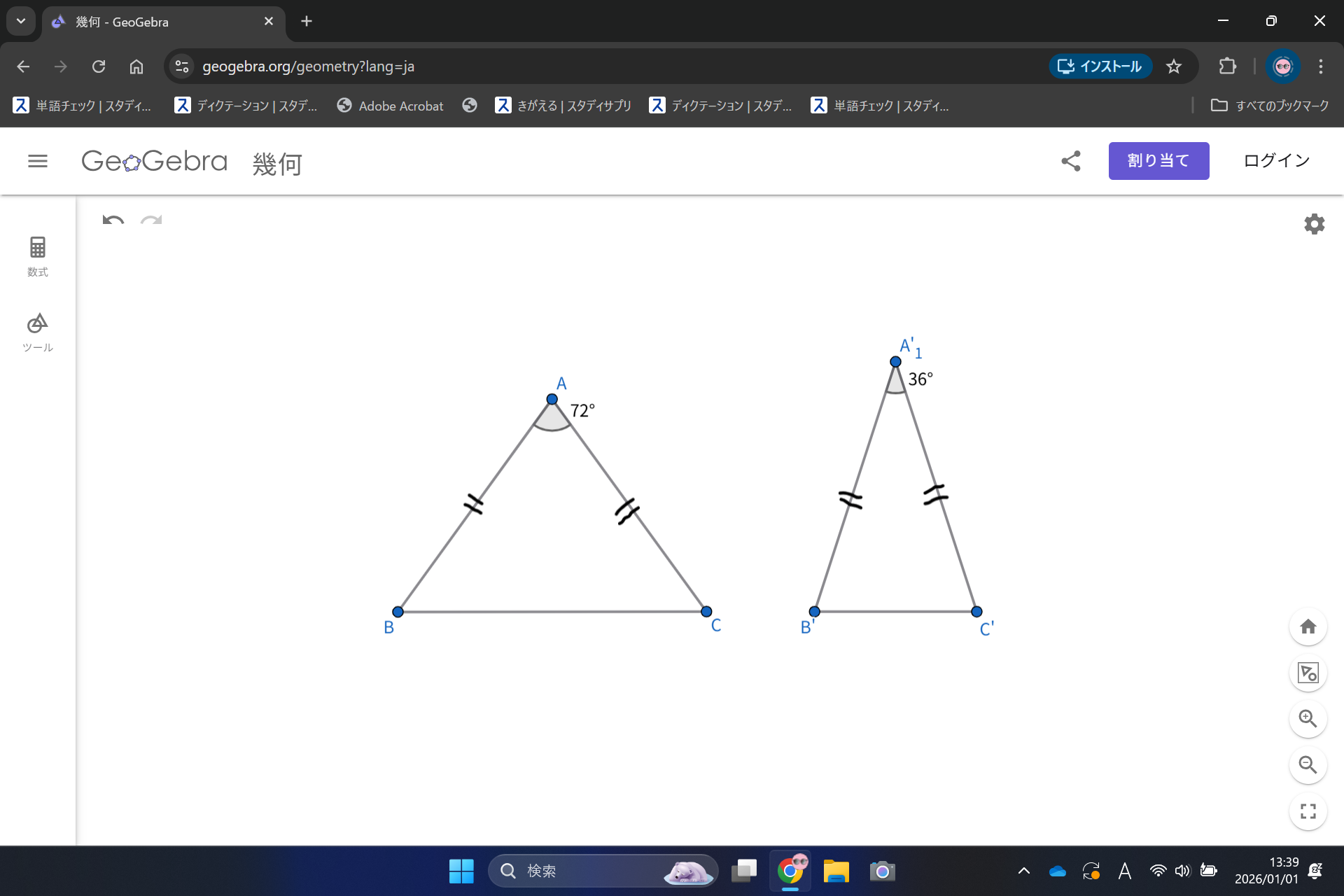思ってた以上にちっちゃかった
で、面積を比較するのですが、もちろん底面と高さはまったく別物で数値も全く公表されてないので、使うのは三角比の面積公式$\frac{1}{2}absin∠C$です.
だから、今回は角度が与えられている$∠A$と$∠A'$を面積公式の$∠C$に当てはめて考えて、$△ABC$は$\frac{1}{2}AB×AC×sin∠C$,$△A'B'C'$は$\frac{1}{2}A'B'×A'C'×sin∠C'$
んで、$AB=AC=A'B'=A'C'$ぬぁぬぉで結局、求めるのは$\frac{sin72^{\circ}}{sin36^{\circ}} $だおっていうことです.
どうします？$cos36^{\circ}$と$sin72^{\circ}$を非自明なものとして出した方がいいですか？もうめんどくさいので$cos36^{\circ}= \frac{1+ \sqrt{5} }{4} $や$sin72^{\circ}= \frac{ \sqrt{10+2 \sqrt{5} } }{4} $の値の導出過程は省いちゃいますか.まあ一応気になる人は....ggrks()
さあじゃあ$cos36^{\circ}= \frac{1+ \sqrt{5} }{4} $ですから、$sin36^{\circ}$は暗算すると$ \frac{ \sqrt{10-2 \sqrt{5} } }{4}$というのが分かります.で、特に解説するところもないからあとは$$\frac{ \sqrt{10+2 \sqrt{5} } }{4} ÷ \frac{ \sqrt{10-2 \sqrt{5} } }{4}=\frac{1+ \sqrt{5} }{2}$$ 黄金比だ. きもひい...
【イ】はもうねこれなんすか問題作ったやつ舐めちょりますね.
正五角形は$△ABC$が五個、正十角形は$△A'B'C'$が十個. なぜか問題文で【ア】と計算式が逆にされてるので、計算は$$\frac{ \sqrt{10-2 \sqrt{5} } }{4}×10 ÷\frac{ \sqrt{10+2 \sqrt{5} } }{4}×5 =\frac{ 2\sqrt{10-2 \sqrt{5} } }{\sqrt{10+2 \sqrt{5} }}=\sqrt{5}-1$$
お綺麗なようで.
んじゃ【ウ】ですね. なんか立体交えてきてすごい問題でも来るのかおもたらこれまた中学生以下の問題. 多分これ作った人は途中で問題作るの飽きたか【エ】～【カ】を元々作ってたけど、なんかもやもやして適当に問題増やしたかのどちらかですね. まあ作ったん僕ですけど.（ｼｯﾃﾙｹﾄﾞ）
正十二面体は正五角形が十二個あるから$△ABC$が全部で60個...え60個！？正気かよこの問題.×60とかめんどいだけじゃないですか.
なので計算は、$$\frac{ \sqrt{10+2 \sqrt{5} } }{4}×60 ÷ \frac{ \sqrt{10-2 \sqrt{5} } }{4}×10=\frac{ 6\sqrt{10+2 \sqrt{5} } }{\sqrt{10-2 \sqrt{5} }} =6×\frac{1+ \sqrt{5} }{2}=3+3\sqrt{5} $$
ey yo 次！
【エ】～【カ】は見ての通り、同じ問題文の穴あきなんですが、まずなんで内接球と外接球が一致するって書き方したかと言うと、自分数学苦手なのでこの柱体の中に正十二面体が内接するかそれとも限界まで大きくして内部に存在するという状態なのかどっちなのかいまいち見当がつかなくて、（たぶん内接しないのかな？論理的に説明できる人求ム）それで一番ピンと頭に来たのがこの問題文.
まず【エ】は柱体$X$の高さが、この内接球の直径と同じくなり、内接球の直径は底面の正十角形の内接円の直径と同じくなります.
つまりは、こんな図ですね.
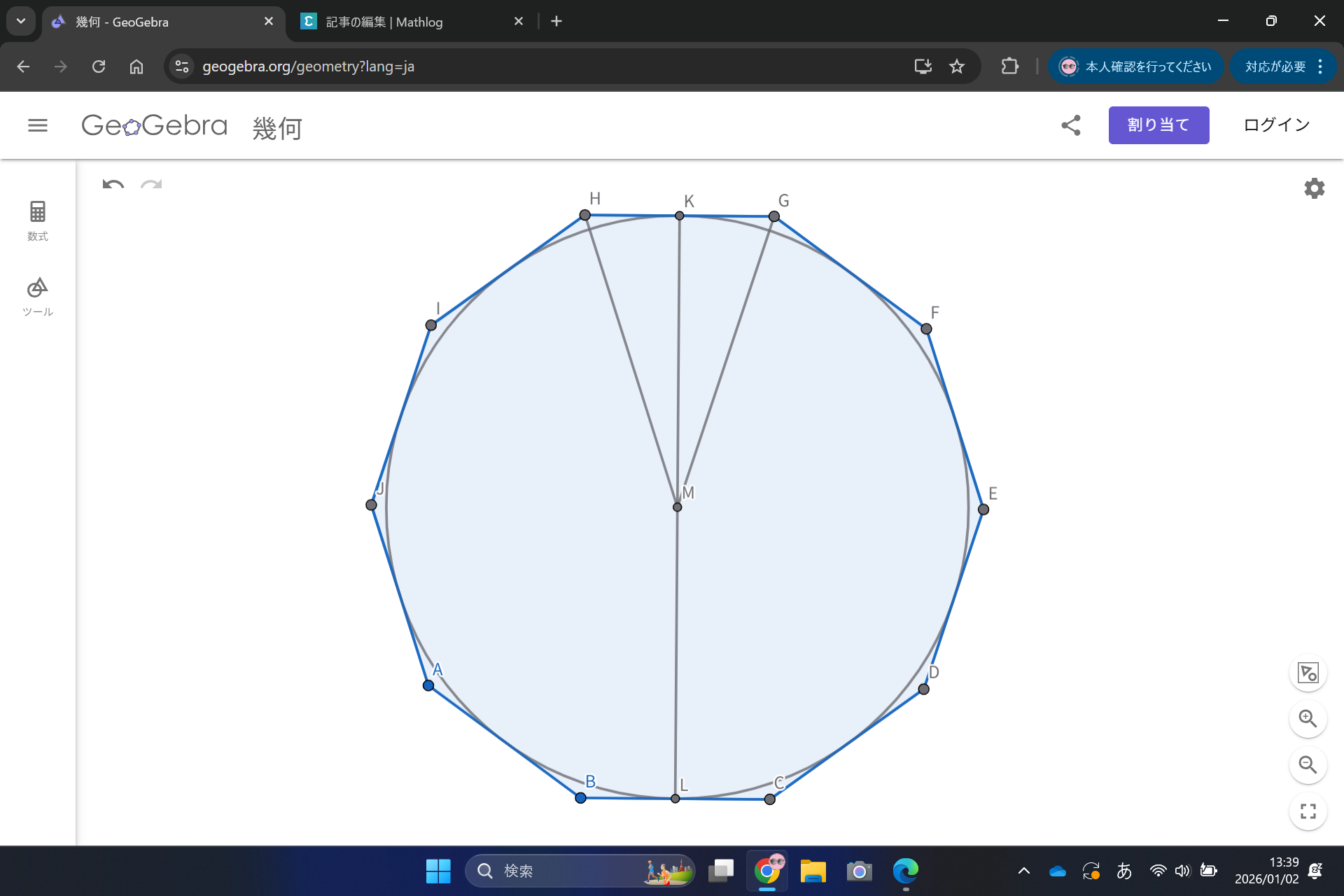ブックマークって勝手につくものなのか？
求めたいのは見えずらいですが、正十角形の生身を一刀両断している$KL$の長さですね. なんかうわさに聞いた話によると正$n$角形の一辺を$a$,内接円の半径を$r$とすると、$r=\frac{a}{2tan(\frac{180 }{n})}$って公式があるらしいですが、なんか気に食わないので公式は使わずに、まず外接円の半径を求める⇒三平方の定理で内接円の半径を求める、って解き方をします.（めんどくさいねぇ）
まず$△HGM$において余弦定理から、$HM=\frac{1+ \sqrt{5} }{2}$ってわかるんで（ん？暗算で$HG^2=HM^2+GM^2-2・HM・GMcos36^{\circ}$を計算しただけだよ？）、$△HKM$において三平方の定理より、$KM=\frac{ \sqrt{5+2 \sqrt{5} } }{2}$とわかって柱体$X$の高さは$\sqrt{5+2 \sqrt{5} }$と求まるワケです.
クソ端折ってガンガン解説していますが、わかりずらかったら申し訳ございませぬ.
次に正十二面体$Y$の一辺を求めていきますが、これまた台風の噂で聞いた話では正十二面体の一辺を$b$,外接球の半径を$R$とすると、$b=\frac{ \sqrt3({\sqrt{5}-1 }) }{3}R$っていう公式があるらしいんですけど、正直めちゃくちゃ使いたいんですが（普通に計算するのだいぶめんどい）使わずに気合いで出していきましょうか. いや正確に言えば、求める過程で最終的に公式が作れますのでそれで解いていきます.
大まかな方針としては、頂点を結び内部に立方体を作る⇒対角線から立方体の一辺を出す⇒正十二面体の一面と立方体の一辺との関係から【オ】を求める、てな方針でございまする.
常識と言えば常識ですが、正十二面体の中に立方体を作ることができます. これに関しては証明もクソもないですから実際に図を見て納得してください.
そして立方体の対角線から～、というのは実際に図を見ればわかりますが、内部にできた立方体の対角線は外接球の直径に等しくなります.
で、これは死んでも忘れちゃいけない公式で立方体の対角線は一辺を$s$とすると、$\sqrt3s$と表される.つまり、外接球半径を$R$としたから、$2R=\sqrt3s$というワケなのでR.
で、値を代入して求めていくのもありかなと思いましたが、無駄にめんどくさいしどうやってあの公式が導かれるのかも一応分かった方がいいかなと思うので、値はまだ代入しません.
次に正十二面体の一面と立方体の一辺の関係によく目を凝らしてください. と言っても、図がないので用意します.［下図参照］
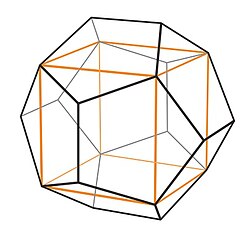機械音痴過ぎてこの画像を編集すらできない人←
で、そのふたつの関係に思い当たる節はありますか？え？正五角形と立方体は美しくて大好き？だ、だめですよ！正五角形と立方体のラブラブな仲に割って入ってドロドロで最終的に誰かは絶対報われず胸糞悪い三角関係なんて.()しかし、そんな三角関係も見方を変えればキラキラ輝く三角関係に生まれ変わります.
つまり茶番が過ぎましたが、立方体の一辺は正五角形の対角線になっているのです. あ知ってました？すみません余計なことに文字数が多くて.
昔中学校の先生に「君は二言(ふたこと)も三言(みこと)も四言(しこと)も余計です！」って言われたことがあって、そのときは「説教してんのにそれはどの口が言ってんねん」って思ってましたね. ――――（中略）
で、正五角形の対角線と言えば、正五角形の一辺$b$（ちなみにさっきから出てくる文字は特にちゃんと言ってないけど、例えのようなものを出すときにつけた文字をそのまま使っています. 結構適当なのでここらへんはあんま意識せず読んでいってください🙇）は対角線$s$と次のような関係があるのは超有名です.
$$ s=\frac{ {1+\sqrt{5} } }{2}b$$
こいつはめっちゃいろんな出し方があるらしいですけど、まあ一番無難なのは相似比とかからでしょうね. まあもし不可思議不可思議転が一知らない人がいたら自力で求めてみてください.
そいなら、$2R=\sqrt{3}s⇔s=\frac{ 2 }{\sqrt{3}}R$と連結させれば、正十二面体の外接円半径$R$と正五角形の一辺すなわち正十二面体の一辺$b$との関係がわかるわけです. これが【オ】を求めるときの冒頭に行った正十二面体の一辺と外接球半径との公式になります.
なので、この後これを計算すると、
$$ b=\frac{ \sqrt3({\sqrt{5}-1 }) }{3}R$$
となるわけです.
あとは、$R=\frac{ \sqrt{5+2 \sqrt{5} } }{2}$を代入して、

\begin{eqnarray} b &=& \frac{ \sqrt{5+2 \sqrt{5} } }{2}\cdot\frac{ \sqrt3({\sqrt{5}-1 }) }{3}\\　 &=& \frac{ \sqrt{3(5+2 \sqrt{5})(\sqrt{5}-1)^2 } }{6} \\ &=& \frac{ \sqrt{3(5+2 \sqrt{5})(6-2\sqrt{5}) } }{6} \\ &=& \frac{ \sqrt{30+6 \sqrt{5} } }{6} \end{eqnarray}
が解となります.すべて$6$を約数に持っていてなんとなくうずうずする人は、$$ b=\sqrt{\frac{5+\sqrt{5}}{6}}$$
としても全然いいと思います. ただ一般的に根号の中に分数があるのはあまり好まれませんから分母の$6$を外に出した形のままでいいと思います.
これで、【オ】も求まりましたので最後に【カ】を華麗に解いて終わりにしてやりましょう.
ちょっと文字が多くなってきたので、ここで整理しておきますね.

最後の【カ】に関しては、もう底面の一辺の長さも高さも正十二面体の一辺の長さも必要なものは全部求まっているので脳死で計算しても全然普通に答えは出せると思います. しかし、数学はどれだけ楽して解を導けるかが重要となってきます. 数学者のほとんどは結局これを追究しています. しらんけど.
なので、より楽で、効率的かつ合理的で宗教的な、いや宗教的じゃなくてもいいですが、とりあえず別の解き方を模索しましょう.

ここで、このような公式はおしりでしょうか？下品ですね.
ここで、このような公式はご存じないでしょうか？
$$ S_{10}=5ar=\frac{5}{2}ah$$

$$ S_{5}=\frac{ 5b^2 }{4tan36°}$$

あ知らなかったですか？安心してください. 僕も知らなかったです. というか、そもそも正十角形も正十二面体もそこらへんの問題ではまずほとんど見かけませんからね. 知らなくて当然です. しかし、知らないからと言って出せないわけでは決してありません.
この公式を頑張って出してみましょう.（頑張って、というほど難しくもないです）
まず$S_{10}=\frac{5}{2}h$から.正十角形を中心から $10$ 個の二等辺三角形に分割すると、その$1$つ分の底辺は$a=1$、高さは内接円半径$r$です.
つまり、
$$ S_{10}=10\times\left(\frac{1}{2}\times 1\times r\right)$$
ですよね。
ここで、柱体$X$の高さ$h$は内接球の直径$2r$と同じでしたから、
$$ r=\frac{h}{2}​$$
これを代入すれば、
$$ S_{10}=5\times\frac{h}{2}=\frac{5}{2}h$$
公式なんて覚えるもんじゃなくて、その場で作るもんなんすよ.（ドヤッ）
次に正五角形の$ S_{5}=\frac{5b^{2}}{4\tan 36^{\circ}}$
これも同じ理屈です.
正五角形を一辺$b$、高さ$r'$の三角形$5$個に分けると、
$$ S_{5}=5\times\left(\frac{1}{2}br'\right)$$
中心角$72^{\circ}$の半分$36^{\circ}$を使って、
$$\tan 36^{\circ}=\frac{b/2}{r'}$$
だから、
$$ r'=\frac{b}{2\tan 36^{\circ}}$$
これをブチ込めば、 $$ S_{5}=\frac{5b^{2}}{4\tan 36^{\circ}}$$
ハイ完成.
では、この「武器」を使って、柱体$X$と正十二面体$Y$の表面積比【カ】を、世界一楽に求めていきましょう.

表面積は「底面$2$枚$+$側面$10$枚」ですね。
$$S_{X}=2\cdot\frac{5}{2}h+10\cdot 1\cdot h=15h $$
シンプルすぎん？

表面積は「正五角形$S_{5}$が$12$枚分」です.
$$S_{Y}=S_{5}×12=\frac{5b^{2}}{4\tan 36^{\circ}}\cdot12=\frac{15b^{2}}{\tan 36^{\circ}}$$
ここで、さっき求めた
$$ b^{2}=\frac{5+\sqrt{5}}{6}$$
と、黄金比の界隈では有名な
$$ \tan 36^{\circ}=\sqrt{5-2\sqrt{5}}$$
を召喚します.
そして、
\begin{eqnarray} S_{Y} &=& 15\cdot\frac{5+\sqrt{5}}{6}\cdot\frac{\sqrt{5+2\sqrt{5}}}{\sqrt{5}}\\　 &=& \frac{5\cdot\sqrt{5}(\sqrt{5}+1)}{2}\cdot\frac{\sqrt{5+2\sqrt{5}}}{\sqrt{5}} \\ &=& \frac{5(\sqrt{5}+1)}{2}\sqrt{5+2\sqrt{5}} \end{eqnarray}
おや……？$\sqrt{5+2\sqrt{5}}$って、これ【エ】で出した高さ$h$そのものじゃね？
つまり、
$$ S_{Y}=\frac{5(\sqrt{5}+1)}{2}h$$
ってことになります.

さあ、計算していきましょう！
$$\text{【カ】}=\frac{S_{X}}{S_{Y}}=\frac{15h}{\frac{5(\sqrt{5}+1)}{2}h}$$
見てください. $h$が消えます.
残ったのは、
$$ \frac{15\cdot 2}{5(\sqrt{5}+1)}=\frac{6}{\sqrt{5}+1}$$
最後にこいつを有理化してフィニッシュ！
$$ \frac{6(\sqrt{5}-1)}{(\sqrt{5}+1)(\sqrt{5}-1)}=\frac{6(\sqrt{5}-1)}{4}=\frac{3\sqrt{5}-3}{2}$$

$$ \text{【カ】}=\frac{3\sqrt{5}-3}{2}$$

これでようやく【ア】～【カ】の合計$6$つの値を求め終わりましたね.
難しかった、というよりやや覚えてないと計算がめんどくさくなるとこはありましたが、まあ多分考え方的にはそんなに難しくないんじゃないかなと.（難しくない、と思って作ったはずなのにGeminiもchatGPTも間違えるし、これは難関大最終大問レベルです～～みたいなこと抜かすから難易度$ ★★☆☆☆$じゃないのかなって不安になりました）
あと【カ】は確かにちょっと強引だったかなとも思ってます. 反省はしてません.
ではこの記事の問題の解答解説はこれにて終了といたします. ここまでお読み詠み黄泉夜見代美頂きありがとうございました.