【相対論】Petrov分類２

Petrov分類の記事一覧

　 Petrov分類1 の続きです。前の記事で導入した記号、概念、命題などはそのまま使います。前回は幾何学寄りの方法でPetrov分類を導入しましたが、今回はより代数的な切り口になっていきます。

principal null vector

　これまではself-dual principal null plane を使ってPetrov分類を行ってきましたが、principal null vectorによる定義もあり、その準備をします。

　まず、self-dual null planeとnull vectorがスカラ倍を除いて一対一に対応することを見ます。　$P_+:V\to U_+$は基底を
\begin{align} &P_+(\sqrt{2}e_1\wedge k)=m\wedge k\\ &P_+(\sqrt{2}e_1\wedge l)=\bar m\wedge l\\ &P_+(2e_3\wedge e_0)=l\wedge k-m\wedge \bar m \end{align}
のように写しました。基底$\{\sqrt{2}e_1\wedge k,\sqrt{2}e_1\wedge l,2e_3\wedge e_0\}$と基底$\{m\wedge k,\bar m\wedge l,l\wedge k-m\wedge \bar m\}$に関する計量はそれぞれ
\begin{align} \begin{pmatrix} 0 & 2 & 0\\ 2 & 0 & 0\\ 0 & 0 & -4 \end{pmatrix},\ \begin{pmatrix} 0 & 1 & 0\\ 1 & 0 & 0\\ 0 & 0 & -2 \end{pmatrix} \end{align}
となることから、$P_+$が相似写像であることも分かりました。

　self-dual null planeを$\beta=m\wedge k$と表します（このとき、$k$は実数倍を除いて一意的に定まることに注意）。　$\beta\in U_+$が定める複素直線を$V$で考えてみます。複素数$\alpha=a+ib$に対して、
\begin{align} P_+^{-1}(\alpha\beta)=\alpha P^{-1}_+(\beta)=(a+b\ast)\sqrt{2}e_1\wedge k=\sqrt{2}(ae_1+be_2)\wedge k \end{align}
なので、$\beta$が定める複素直線は$V$では$\{x\wedge k;\ x\perp k,\ x:\textrm{spacelike}\}$という集合になります。これは本質的にはnull vector $k$のみで決まります。逆に、null vector $k$ に対して、$x\perp k$となる任意のspacelike vector $x$を取り、$x\wedge k$を$P_+$で写したものは、self-dual null planeを複素数倍の不定性を除いて一意的に定めます。このようにself-dual null planeとnull vectorは互いに複素数倍と実数倍を除いて対応しています。self-dual null plane $\beta$が定めるnull vectorの直線を$N(\beta)$と書くことにして、次のように定義します。

principal null vector の重複度

　self-dual principal null plane $\beta$に対応するprincipal null vector $k\in N(\beta)$の重複度を$\beta$の重複度として定義します。このとき、次の命題が成り立ちます。

　またprincipal null vectorの重複度を使ってPetrov分類を行うことができます。これは前の記事のPetrov分類の同値な2つの定義を考えれば自明な言い換えです。

　それぞれのtypeの状況を図で表す以下のような表記法があります。
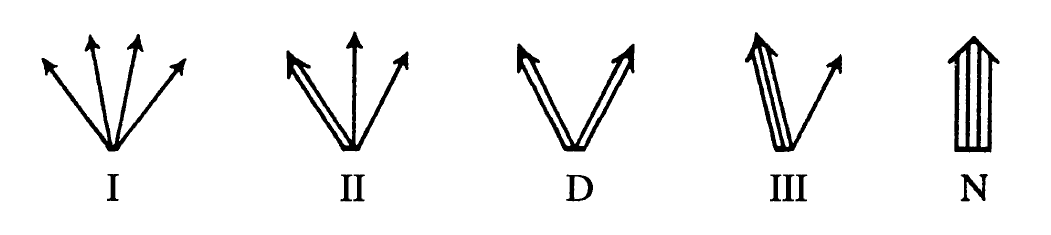Petrov分類のprincipal null vectorによる表現

Jordan標準形によるPetrov分類

　3つ目の分類方法は$\mathbb{W}_+$のJordan標準形による方法です。

　$tr\mathbb{W}_+=0$なので、$\mathbb{W}_+$のJordan標準形として可能な形は以下になります。
まず、3つの異なる固有値を持つ場合は、固有空間でない一般固有空間はあり得ないので
(Jordan-I)
\begin{align} \mathbb{W}_+\sim\begin{pmatrix}\lambda_1 & 0 & 0\\0 & \lambda_2 & 0\\0 & 0 & \lambda_3\end{pmatrix},\ \sum_i\lambda_i=0 \end{align}
という形になります。次に2つの固有値を持つ場合は、一つの固有値に関して2次元の固有空間がある場合と2次元の固有空間でない一般固有空間がある場合があるので、
(Jordan-II)
\begin{align} \mathbb{W}_+\sim\begin{pmatrix}-2\lambda & 0 & 0\\0 & \lambda & 1\\0 & 0 & \lambda\end{pmatrix},\ \lambda\ne0 \end{align}
(Jordan-D)
\begin{align} \mathbb{W}_+\sim\begin{pmatrix}\lambda & 0 & 0\\0 & \lambda & 0\\0 & 0 & -2\lambda\end{pmatrix},\ \lambda\ne0 \end{align}
となります。最後に固有値が一つの場合は０になるしかないので、3次元の固有空間でない一般固有空間を持つ場合、1次元の固有空間と2次元の固有空間でない一般固有空間を持つ場合、０行列の場合があるので、
(Jordan-III)
\begin{align} \mathbb{W}_+\sim\begin{pmatrix}0 & 1 & 0\\0 & 0 & 1\\0 & 0 & 0\end{pmatrix} \end{align}
(Jordan-N)
\begin{align} \mathbb{W}_+\sim\begin{pmatrix}0 & 1 & 0\\0 & 0 & 0\\0 & 0 & 0\end{pmatrix} \end{align}
(Jordan-O)
\begin{align} \mathbb{W}_+\sim O \end{align}
となり、この6種類は背反であり、これで全部です。

　全てのPetrov分類の$\mathbb{W}_+$は上記の6種類のどれかになるので、それを見ていきます。

Petrov type Nのとき
\begin{align} \mathbb{W}_+=\begin{pmatrix}0 & \Psi_{4} & 0\\0 & 0 & 0\\0 & 0 & 0\end{pmatrix} =\begin{pmatrix}\Psi_{4} & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{pmatrix}^{-1} \begin{pmatrix}0 & 1 & 0\\0 & 0 & 0\\0 & 0 & 0\end{pmatrix} \begin{pmatrix}\Psi_{4} & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{pmatrix}\sim \begin{pmatrix}0 & 1 & 0\\0 & 0 & 0\\0 & 0 & 0\end{pmatrix} \end{align}
となるので、これはJordan-N型です。

Petrov type IIIのとき
\begin{align} \mathbb{W}_+=\begin{pmatrix}0 & \Psi_{4} & - 2 \Psi_{3}\\0 & 0 & 0\\0 & \Psi_{3} & 0\end{pmatrix} =\begin{pmatrix}- 2 \Psi_{3}^{2} & \Psi_{4} & 0\\0 & 0 & 1\\0 & \Psi_{3} & 0\end{pmatrix}^{-1} \begin{pmatrix}0 & 1 & 0\\0 & 0 & 1\\0 & 0 & 0\end{pmatrix} \begin{pmatrix}- 2 \Psi_{3}^{2} & \Psi_{4} & 0\\0 & 0 & 1\\0 & \Psi_{3} & 0\end{pmatrix}\sim \begin{pmatrix}0 & 1 & 0\\0 & 0 & 1\\0 & 0 & 0\end{pmatrix} \end{align}
となるので、これはJordan-III型です。

Petrov type Dのとき
\begin{align} \mathbb{W}_+=\begin{pmatrix}- \Psi_{2} & 0 & 0\\0 & - \Psi_{2} & 0\\0 & 0 & 2 \Psi_{2}\end{pmatrix} \end{align}
となるので、これはJordan-D型です。

Petrov type IIのとき、重複度2のprincipal null vectorが1つだから、self-dual nullの固有ベクトルは1つだけで、その固有値は０でないです。０でない固有値を持って、type Dでないから、Jordan-I or IIです。$\mathbb{W}_+$は$g(\beta,\mathbb{W}_+\gamma)=g(\mathbb{W}_+\beta,\gamma)$を満たすから、異なる固有値に関する固有ベクトルは直交します。固有ベクトルの1つがnullのとき異なる固有値を3つ持つことは不可能なので、異なる固有値は2つです。従ってJordan-II型となります。

Petrov type Iのとき、重複度1のprincipal null vectorしかないので、self-dual nullの固有ベクトルは存在しない。従って、Jordan-I以外はあり得ないから、Jordan-I型である。

　以上より3つ目のPetrov分類の同値な定義を得ます。

　各Petrov typeのJordan分解の様子を象徴的に表した図として以下のようなものがあります。
$\mathbb{W}_+$の固有ベクトルと一般固有空間の様子を表す図