大学数学基礎解説

誤った数学的帰納法で誤った命題を証明する

数学的帰納法,平面の直線による分割

399

誤った数学的帰納法

誤った数学的帰納法を使うと…3!=3 に続いて、数学的帰納法の原理の命題を誤解して使用すると誤った命題も証明できてしまうという別の例を思いついた。

数学的帰納法

( $P (1) \land \forall k \in N; (P (k) ⟹ P (k + 1))$ )
$⟹ \forall n \in N; P (n)$

数学的帰納法

$P (1)$
どんな自然数 $k$ に対しても $P (k) ⟹ P (k + 1)$

が成立するならば、
任意の自然数 $n$ に対して $P (n)$

を誤解していると思われる

誤った数学的帰納法

( $P (1) \land$ $\exists$ $k \in N; (P (k) ⟹ P (k + 1))$ )
$⟹ \forall n \in N; P (n)$

誤った数学的帰納法

$P (1)$
ある自然数 $k$ に対して $P (k) ⟹ P (k + 1)$

が成立するならば、
任意の自然数 $n$ に対して $P (n)$

平面を直線で分割する

平面に直線を描くと、平面を2個の領域に分割できる。
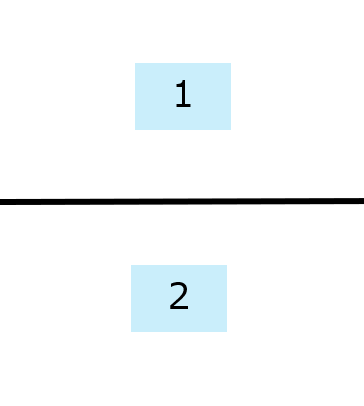直線による平面の分割
そこに最初の直線とは平行にならない2つ目の直線を描くと、平面は領域4個に分割される。
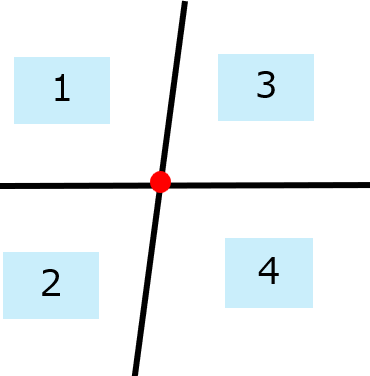2本の直線による平面の分割

直線による分割した後の領域の数を考える

直線 $0$ 本で $1$ 個の領域
直線 $1$ 本で $2$ 個の領域
直線 $2$ 本で $4$ 個の領域
なので、領域の数は線の数が増えるごとに $2$ 倍になっているように見える。

実は誤った命題

P (n)

$n$ 本の直線で平面は最大 $2^{n}$ 個の領域に分割できる

（実は誤り）数学的帰納法？を用いる

$1$ 本の直線で平面は $2$ 個の領域に分割できる。つまり $P (1)$ が成立。
冒頭に書いた通り、さらにもう $1$ 本の直線を適切に描くと、もう一つの直線が $P (1)$ による $2$ つの領域を、それぞれ $2$ 分割するので、 $2^{2} = 4$ 個の領域に分割できる。 $P (2)$ が成立。つまり、 $P (1) \Rightarrow P (2)$ が成立

ここで、誤った数学的帰納法を使用する。
$k = 1$ とすると $P (1)$ と $P (1) \Rightarrow P (2)$ が成り立つので、任意の自然数 $n$ に対して $P (n)$ が成立。つまり「 $n$ 本の直線で平面は最大 $2^{n}$ 個の領域に分割できる。」∎

しかし実際に平面に直線を描くと…

実際に $2$ 本の直線で $4$ つの領域に分割されているところに、 $3$ 本目の直線を描くと...
どうやっても、最大で $7$ 個の領域にしか分割できないことがわかる。すでにある交点を通るようにしたり、すでにある直線に平行に引いたりすると $6$ 個の領域に分割できるが、 $8$ 個の領域になるようには分割できない。
$P (3)$ 「 $3$ 本の直線で平面は最大 $2^{3} (= 8)$ 個の領域に分割できる。」は偽である。
このように誤った数学的帰納法を使用すると誤りである命題も証明できてしまう。
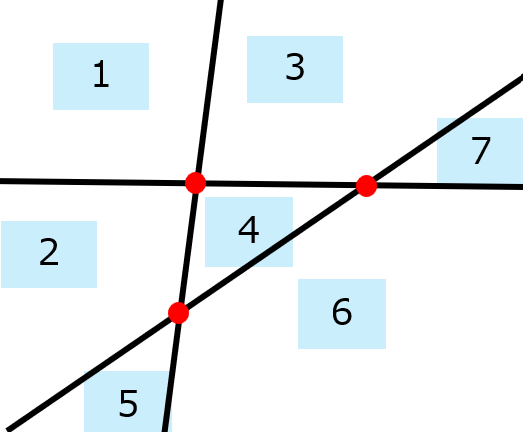3本の直線による平面の分割

平面を直線で分割した時の領域の最大個数はいくつか？

数学的帰納法を正しく使う

命題

Q (n)

$n$ 本の直線で平面は最大 $\frac{1}{2} (n^{2} + n + 2)$ 個の領域に分割できる

数学的帰納法を用いる

$n = 1$ の時、 $\frac{1}{2} (n^{2} + n + 2) = \frac{1}{2} (1^{2} + 1 + 2) = 2$ なので
$Q (1)$ が成立。
$\forall k \in N; Q (k)$ が成立と仮定する。 $k$ 本の直線で平面が $\frac{1}{2} (k^{2} + k + 2)$ 個の分割されているとする。
そこに、もう $1$ 本の他のどの直線とは平行にならずに既存の交点を通らない直線を描く。（できる領域の個数が最大になるようにしている）
そうすると、この直線はすでにある $k$ 本の直線と交わる。この直線上に交点は $k$ 個ある。直線がこれらの交点によって $k + 1$ 個の区間に分割される。直線が通る各領域（直線 $k$ 本で分割された各領域）はこれらのそれぞれの区間（直線との共通部分）によって $2$ 分割されるので、新たに $k + 1$ の領域が増える。
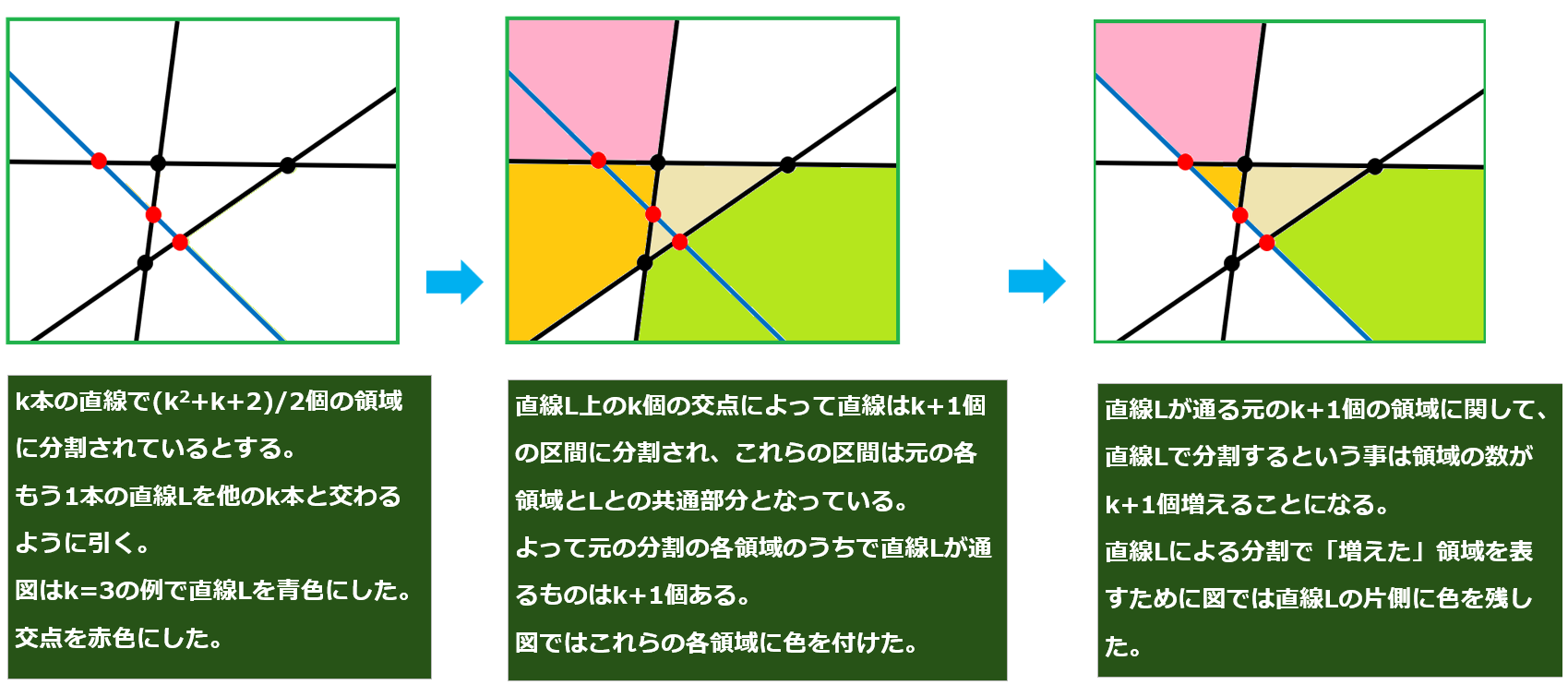新たな直線による分割
領域の数は
$\frac{1}{2} (k^{2} + k + 2) + (k + 1)$
$= \frac{1}{2} (k^{2} + k + 2 + 2 k + 2)$
$= \frac{1}{2} ((k + 1)^{2} - 1 + k + 2 + 2)$
$= \frac{1}{2} ((k + 1)^{2} + k + 1 + 2)$
$= \frac{1}{2} ((k + 1)^{2} + (k + 1) + 2)$
となり、新たに引いた直線はそれと平行でない他の $k$ 本の直線とは $k$ 回交わるだけなので、これより多い個数の領域には分割できない。 $Q (k + 1)$ が成り立つ。
任意の $k \in N;$ $n = k$ のときの $Q (k) \Rightarrow Q (k + 1)$ が示せた。 $Q (1)$ と合わせて、数学的帰納法を適用すると、任意の自然数 $n$ に対して $Q (n)$ が成立する。
よって、 $n$ 本の直線で平面は最大 $\frac{1}{2} (n^{2} + n + 2)$ 個の領域に分割できる∎

おわりに

数学的帰納法の確かめるべき条件を誤解すると、誤った命題を証明できてしまうという簡単な例を紹介した。
数列の一般項のような簡単な事にもある一つの一般化の推測が正しいとは限らない例にもなっている。
$n = 0, 1, 2$ と $3$ 以上が大きく異なる現象の一例にもなっている。先日 $X$ で、そういう現象に関する投稿を見かけたので、自分もいくつかの例を挙げてみた。その一つの例で、誤った数学的帰納法で誤った命題を証明する例にもなると思いこの記事を書いた。
これもまた、難しい本を読まなくても難しい問題を解かなくてもできる数学の楽しみ方の一つと言える。

投稿日：20日前

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

IIJIMAS

3731

他の人のコメント

コメントはありません。

読み込み中

IIJIMAS

誤った数学的帰納法で誤った命題を証明する

誤った数学的帰納法
直線による分割した後の領域の数を考える
平面を直線で分割した時の領域の最大個数はいくつか？
おわりに