局所同相写像としての層
こないだお茶をしながら話す機会があった(勉強中の)話を復習がてらまとめます。定義そのものはそれほど重くなく、ささっと終わらせることができてしまうところ、それを補完するための「気持ち」を書いた地の文が(特に最初の方は)多くなっています。
本稿の話の核にある数学的内容はほとんどTakeuchiSCT(pp.11-20)に書かれているものではありますが、僕の捉え方に沿って話の構成を組み替えたり、例を差し込んだり、追加で色々示したものが本稿になっています。基本的な定義をもう知っている人向けに言えば、位相空間$X$上の層の圏$\mathbf{Shv}_X \subseteq_\mathrm{cat} \mathbf{Set}^{\langle\mathcal{O}_X, \supseteq\rangle}$と$X$を余域に持つ局所同相写像(étale空間)の圏$\mathbf{\acute{E}t}_X \subseteq_\mathrm{cat} \raise{0.2em}{\mathbf{Top}}\left/\raise{-0.2em}{X}\right.$の間の圏同値 $\mathbf{Shv}_X \underset{\mathrm{Sections}}{\overset{\mathrm{Stalks}}\longleftrightarrows} \mathbf{\acute{E}t}_X$がある(nlab-etale-space)のですが、$\mathbf{\acute{E}t}_X$の対象のことを層と呼ぶことからはじめて、これがそもそもどういったものなのか、という話をするのと、この圏同値の$\mathrm{Stalks} \circ \mathrm{Sections} \cong \mathrm{id}_{\mathbf{\acute{E}t}_X}$の自然性を除く部分を直接的に示すことをします。これに伴って、芽の概念を位相空間上の関数に関する芽に特殊化して定義しています(auxiliary-defs-to-define-germs)(一般の$\mathbf{Set}$-valuedな前層$F \in \mathbf{Set}^{\langle\mathcal{O}_X, \supseteq\rangle}$についても、$\upharpoonright_V$を制限写像$F(U \supseteq V): F(U) \rightarrow F(V)$に読み替えることで容易に定義を一般化できます)。
「位相空間上の層」の概念は二つの(圏同値の意味で)同値な特徴付け(関手$\langle\mathcal{O}_X, \supseteq\rangle \rightarrow \mathbf{Set}$であって一定の貼り合わせ条件を満たすものとしての層と、底空間への局所同相写像としての層)を持っており、それぞれが少しずつ異なる側面から層という概念を見つめるものになっています。
本稿は、層の概念がそもそも何を表現しようとしているのかというのを明らかにしつつ、後者の「底空間への局所同相写像としての層」の概念への道のりを紹介します。前半は気持ちの話ばかりするのであまり証明を書いていませんが、終盤の定理群の証明を追うには連続関数・部分空間位相・開基辺りの取り扱いにある程度慣れている必要があるかもしれません。
グラフの重ね合わせとしての層
位相空間$(X, \mathcal{O}_X)$上の層$\mathcal{F}$は、大変ざっくり言えば、$X$の開集合が定義域になっているような関数のなんらかの集まり$C_\mathcal{F}$(関数全部、連続関数全部、正則関数全部、など)を持ってきて、それら関数の集合論的グラフ(関数$f:U\rightarrow X$についての$\{ (u, x) \in U \times X \mid f(u) = x \}$。これを$\mathrm{Graph}_f$とでも書くことにします)を全部一度に「重ね合わせた」ような位相空間です。グラフを「重ね合わせる」わけですから、一つの関数のグラフともう一つの関数のグラフが部分的に一致している時には、それらを二枚の全く異なるグラフとして考えるのではなく、一致している部分については同じグラフであるとして貼り合わせるようにします(きちんとした定義は後に回します。一旦、このようなふわっとしたイメージのまま話をさせてください)。
正則関数の層
例えば、$\mathbb{C}$上の層$\mathcal{F}_\mathrm{holo}$として、各$U \subseteq^{\mathrm{open}} \mathbb{C}$上で定義された正則関数(holomorphic function、即ち、各点複素微分可能な関数)すべてのグラフを重ね合わせたようなものが考えられるでしょう。つまり、$C_{\mathcal{F}_\mathrm{holo}} = \set{ f \mid U \subseteq^\mathrm{open} \mathbb{C} \text{ , } f : U \rightarrow \mathbb{C} \text{ は正則}}$として、これら正則関数の関数のグラフをどうにかして全部一挙に重ね合わせるということを考えたいわけです。
ところでそもそも、$f \in C_{\mathcal{F}_\mathrm{holo}}$のグラフというのは$\mathrm{dom}(f) \times \mathbb{C} \subseteq \mathbb{C} \times \mathbb{C}$の部分集合になっているわけなので、$f$のグラフを「描く」先の空間というのは、普通に考えれば、$\mathbb{C} \times \mathbb{C}$になっています(別の例を出しておくと、例えば、$S^2 \rightarrow \mathbb{R}^3$の連続関数(つまり、球面を三次元空間に描画するような連続関数)のグラフというのは$S^2 \times \mathbb{R}^3$に「描か」れますし、最も慣れ親しんでいるであろう実引数実関数$\mathbb{R} \rightarrow \mathbb{R}$のグラフは$\mathbb{R} \times \mathbb{R}$に描かれます)。
グラフを「重ね合わせる」方法として最も素朴であろう方法というのは、$\mathbb{C} \times \mathbb{C}$の中の$f$のグラフ$\mathrm{Graph}_f$に相当する部分を「塗りつぶす」という操作を各$f \in C_{\mathcal{F}_\mathrm{holo}}$について繰り返していくというものです。つまり、重ね合わせの結果として、集合
$$
\left(\bigcup_{f \in C_{\mathcal{F}_\mathrm{holo}}} \mathrm{Graph}_f \right)\subseteq \mathbb{C} \times \mathbb{C}$$
を考えようというやり方です。$f \in C_{\mathcal{F}_\mathrm{holo}}$の$\mathrm{Graph}_f$を集合和に加えるたびに、$\mathrm{Graph}_f \subseteq \mathbb{C}\times\mathbb{C}$が塗りつぶされていくという算段なわけです。
しかし、実のところ、これは全くうまくいきません。というのも、各$(z_1, z_2) \in \mathbb{C}\times\mathbb{C}$は定数関数$(z \in \mathbb{C}) \mapsto z_2$のグラフに含まれてしまっていて、定数関数は当然のように正則で$C_{\mathcal{F}_\mathrm{holo}}$の元になっていますから、$\bigcup_{f \in C_{\mathcal{F}_\mathrm{holo}}} \mathrm{Graph}_f$は定数関数のグラフの和をとった時点で$\mathbb{C}\times\mathbb{C}$全域になってしまっています。グラフをただ単に描くというのを繰り返してしまうと描く先の空間をすべて塗りつぶしてしまって、どんなグラフが描かれていたのか、という情報が完全に失われてしまうのです。
つまり、層を考える上では、点$(z, w) \in \mathbb{C}^2$が何らかの正則関数によって通過されているとき、これがどのように正則関数によって通過されたのか、という情報をグラフの各点に書き残しておきたいということになります。大雑把なアイデアとしては、関数$f: U \rightarrow \mathbb{C}$と定義域の点$z_0 \in U$とがあったとき、先ほどと同じく$\mathrm{Graph}_f$内の$(z_0, f(z_0))$に相当するものを描いていくわけなのですが、ここで単に$(z_0, f(z_0))$という点をプロットするのではなく、$(z_0, \text{「$f$が $(z_0, f(z_0))$ をどのように通過しているのか」})$という組を集めていく、という、そういうことをやりたいのです。
すると、「$f$が$(z_0, f(z_0))$をどのように通過しているのか」というふわっとした話をどのように厳密に記述すればよいのかというのが問題になってきます。今は正則関数を考えていて常に微分ができますから、まずは導関数たちを使ってこれを記述してみるということを考えます。
例えば、$(0, 1)$は定数関数$\mathrm{const}_1 = (z \in \mathbb{C}) \mapsto 1$によっても$(z \in \mathbb{C}) \mapsto z + 1$によっても踏まれる点ですが、定数関数は$(0, 1)$を通る時に傾き$0$なのに対し、$(z \in \mathbb{C}) \mapsto z + 1$は傾き$1$になっています。このように、傾きが異なることを以て、$\mathrm{const}_1$と$(z \in \mathbb{C}) \mapsto z + 1$が$0$を通過するときの挙動が違うのだ、と主張することができます。
![!FORMULA[63][872907372][0]を通る、傾きが異なる二つの関数](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FfZAgzaP7OPXXLipyEsdj.png?alt=media) $(0, 1)$を通る、傾きが異なる二つの関数
$(0, 1)$を通る、傾きが異なる二つの関数
$(0, 1)$は$\cos$によっても通過されます。$\cos$と$\mathrm{const}_1$が$(0, 1)$を通過するときの様子はどう異なるでしょうか?先ほどの$(z \in \mathbb{C}) \mapsto z + 1$との比較とは異なり、$0$での一階微分はどちらも消えています。しかし、高次の微分を見てみると、例えば二階微分が異なっています。これはTaylor展開を考えるとわかります。
$$ \begin{array}{} % 最悪の空白調整すぎる 助けて~ \mathrm{const}_1(z) & = & 1 & \!\!\!+\!\!\! & 0z & \!\!\!+\!\!\! & 0z^2 & \!\!\!+\!\!\! & 0z^3 & \!\!\!+\!\!\! & 0z^4 & \!\!\!+\!\!\! & \cdots & \!\!\!+\!\!\! & 0z^{2n} & \!\!\!+\!\!\! & 0z^{2n+1} & \!\!\!+\!\!\! & \cdots \\ \cos z & = & 1 & \!\!\!+\!\!\! & 0z & \!\!\!+\!\!\! & \tfrac{-1}{2!}z^2 & \!\!\!+\!\!\! & 0z^3 & \!\!\!+\!\!\! & \tfrac{1}{4!}z^4 & \!\!\!+\!\!\! & \cdots & \!\!\!+\!\!\! & \tfrac{(-1)^n}{(2n)!}z^{2n} & \!\!\!+\!\!\! & 0z^{2n+1} & \!\!\!+\!\!\! & \cdots \end{array} $$
正則性というのは極めて強い制約で、よく知られているように、$U \subseteq^{\mathrm{open}} \mathbb{C}$上の関数$f : U \rightarrow \mathbb{C}$があったとき、$f$が正則であることと$f$が各点Taylor展開可能(解析的)であることは一致します。すなわち各$f \in C_{\mathcal{F}_\mathrm{holo}}$は、各点$z_0 \in \mathbb{C}$においてTaylor級数が正の収束半径$r_{z_0} \in \mathbb{R}_{>0}$を持っているわけで、Taylor級数が開球$B_{z_0, r_{z_0}} = \{ z \in \mathbb{C} \mid |z-z_0| < r_{z_0} \}$内の$f$の挙動を完全に説明しきっています。つまり、各$z_0$についての$z_0$周りの$f$のTaylor級数は、$f$が「どのように」$(z_0, f(z_0))$を通過しているのかという情報を与えています。
話を戻すと、今は正則関数のグラフをすべて一挙に描いたような空間$\mathcal{F}_\mathrm{holo}$を作りたくて、グラフをただ単に$\mathbb{C}\times\mathbb{C}$上に塗りつぶす形で置いていくのではなく、入力座標と、グラフの各点がどのような挙動を持つ関数によってもたらされているのか、という情報の組をかき集めればよいのではないか、という話でした。このアイデアをTaylor級数の話を踏まえて実現しようとすると、次のようなものが出来上がります。
$$ \mathcal{F}_\mathrm{holo} \overset{?}{:=} \left\{ \left(z_0, \{a_k\}_{k \in \mathbb{N}} \right) \in \mathbb{C}\times\mathbb{C}^\mathbb{N} \;\middle|\; \text{冪級数 $\sum_{k = 0}^{+\infty}a_k(z-z_0)^k$ は正の収束半径を持つ} \right\} $$
正則関数$f: U \rightarrow \mathbb{C}$と$z_0 \in U$が与えられたとき、$z_0$周りのTaylor級数$\sum_{k=0}^{+\infty} \frac{f^{(k)}(z_0)}{k!}(z-z_0)^k$は正の収束半径を持っていますから$\left(z_0, \left\{ \frac{f^{(k)}(z_0)}{k!} \right\}_{k \in \mathbb{N}}\right) \in \mathcal{F}_\mathrm{holo}$になっていて、これが$z_0$を$f$が「どう」通過したのか、という情報を記録しているということになっています。$z_0$周りでの挙動が異なる$f_1, f_2 : U \rightarrow \mathbb{C}$を持ってくれば、これらは$z_0$周りで異なるTaylor級数を持っていますから、記録される組というのもまた異なってきます。つまり、$\mathcal{F}_\mathrm{holo}$がやっていることとしては、各点$z_0$について、$z_0$の周りで$C_{\mathcal{F}_\mathrm{holo}}$の要素たちによって取られ得るすべての挙動を過不足なく集めてきているというわけです。(注:$U$が非連結のときには、「$f_1 \neq f_2$であるが、$z_0$を含む連結成分$V$上では$f_1$と$f_2$が一致している」ということがあり得ます。しかし、その事実は組$\left(z_0, \left\{ \frac{{f_1}^{(k)}(z_0)}{k!} \right\}_{k \in \mathbb{N}}\right) = \left(z_0, \left\{ \frac{{f_2}^{(k)}(z_0)}{k!} \right\}_{k \in \mathbb{N}}\right)$には反映されません。この組は局所的な挙動のみを捉えている、といえます。)
ここで、$\left\{ \frac{f^{(k)}(z_0)}{k!} \right\}_{k \in \mathbb{N}}$の初項は$f(z_0)$ になっていますから、$f$が$z_0$においてどのような値を取っていたのか、という(一番最初の試みでは$\mathbb{C}\times\mathbb{C}$の第二成分にそのまま書き込んでいた)情報は$\left(z_0, \left\{ \frac{f^{(k)}(z_0)}{k!} \right\}_{k \in \mathbb{N}}\right)$にも含有されています。つまり、ただ単に$\mathbb{C}\times\mathbb{C}$に組$(z_0, f(z_0))$を書き込んでいった時よりも豊かな情報を集めてきている、ということになります。これによって、$\mathbb{C}\times\mathbb{C}$にグラフを描いていったときのような、描く先の空間がすべて塗りつぶされてしまって、元のグラフの形が全く分からなくなってしまった、という事態が回避できているのです。
![!FORMULA[119][36974077][0]の周りで正則関数が取り得る「挙動」というのがすべて集めてこられている](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FOiWqhIT6NTZm0BnMQsq5.png?alt=media) $z_0$の周りで正則関数が取り得る「挙動」というのがすべて集めてこられている
$z_0$の周りで正則関数が取り得る「挙動」というのがすべて集めてこられている
$\overset{?}{:=}$などと書いていますから、あぁなんだ、これもまた結局定義として不適切なんじゃないか、はやく真の定義を見せろ、などと言いたくなるかもしれませんが、実のところ、これを$\mathcal{F}_\mathrm{holo}$の定義だと思って問題ありません。というのも、まだ$\mathcal{F}_\mathrm{holo}$にどう位相を入れて空間としての形を形成するか、という話をしていないですから、このままでは位相空間の定義として不十分になっているというだけで、上のように定義された集合に適切で自然な位相を入れることで、次に紹介する方法で定義できる$\mathcal{F}_\mathrm{holo}$と同相な空間が得られるからです。
具体的にどう位相を入れれば良いのか、というのは、次の節で芽の概念を紹介した後に述べます。
芽の空間としての層
芽
先ほどの$\mathcal{F}_\mathrm{holo}$の定義(?)では、正則関数の局所的な記述としてあり得るTaylor級数を各点でかき集めてくることで、正則関数の層という位相空間(と位相を適切に入れることで同相になるような集合)を構成しました。
次の話題として、$U \subseteq^\mathrm{open} \mathbb{R}$上で定義される実連続関数$U \rightarrow \mathbb{R}$のグラフたちを同じように重ね合わせて層を作ることはできるか、というのを考えます。これは、少なくとも、先ほどのようにTaylor級数をかき集めてくることでは実現できません。実連続関数は一般にはTaylor展開ができない(そもそも一階微分可能である保証すらない)ため、各$x_0 \in \mathbb{R}$の周りで正の収束半径を持つTaylor級数の係数列を「$x_0$の周りの関数の局所的な挙動」としてかき集めてきても、解析的関数のクラスの挙動しか捉えることができないからです。このような情報の集め方では、例えば、$(x \in \mathbb{R}) \mapsto |x|$といった微分不能関数の微分不能点(この場合は$0$)周りでの挙動というのを層として取りこぼしてしまうのです。
この状況は、一番最初に$\mathcal{F}_\mathrm{holo}$を作ろうとしたときに$f(z_0)$のみを$z_0$周りの$f$の挙動と捉えてうまくいかなかったのと少し似たような事態になっています。結局、冪級数は「$x_0$の周りの連続関数の局所的な挙動」をエンコードするデータとしては貧弱すぎて、グラフの形という情報を失わずに空間(今考えている空間というのは、「Taylor展開の中心点と、その開近傍で収束する冪級数の係数列」の集合)に点をプロットする、ということを十分に支援できないのです。正則(つまり、解析的)関数のクラスに対しては冪級数が関数の局所的な挙動を記述しきれていましたが、この前提が崩れているのです。
ではどうすれば良いか、というのを考えてみます。まず当たり前のことを言うようですが、冪級数(の係数列)というのは解析的関数の局所的な挙動のエンコードにはなっていますが、解析的関数そのものではありません。一般の実連続関数の局所的な挙動が冪級数としてエンコードできないというのが問題なのですから、そもそもこういった、実数列のような簡潔なデータに局所的挙動をエンコードしようとしたりするのをやめて、実連続関数の生の挙動をそのまま局所的挙動の記述として持ってくるといいのではないか、という発想が出てきます。つまり、関数の局所的挙動を級数のような整然としたデータとして記述しなおすというのをあきらめて、実際の観測結果そのものをそのまま持ってきて、それを(局所的挙動の)記述なのだ、と言い張るということです。
この考えを定式化しているのが芽(germ)と呼ばれる概念です。
芽の概念を述べるために、まず、補助的な集合と関係を定義します(これらの名前や記法はいずれも非標準的です)。
$(X, \mathcal{O}_X)$を位相空間、$Y$を集合、$x_0 \in X$とする。
$x_0$の周りを通る関数そのものたちの集合として
$$
\begin{align}
\mathrm{LocalFns}_{X,Y,x_0} &:= \left\{ f \text{$\mid U \subseteq^\mathrm{open} X$, $x_0 \in U$, $f : U \rightarrow Y$} \right\} \\
&\subseteq\ Y^X
\end{align}
$$
とおく。
$\mathrm{LocalFns}_{X,Y,x_0}$上の関係$\sim_{x_0}$を、
$$ f \sim_{x_0} g \;:\Longleftrightarrow\; \text{$x_0$ の開近傍 $W \in \mathcal{O}_X$ が存在して、$W \subseteq \mathrm{dom}(f) \cap \mathrm{dom}(g)$ かつ $f\upharpoonright_W = g\upharpoonright_W$} $$
と定め(ここで、$f\upharpoonright_W$は$f$の$W$への制限)、$f \sim_{x_0} g$のとき$f$と$g$は$x_0$の周りで局所的に同一と言うことにする。すると、$\sim_{x_0}$は同値関係である(反射性と対称性は明らかで、開近傍と開近傍の共通部分が開近傍になるため推移性が言える)。
そこで、$x_0$の周りで関数が局所的に取り得る挙動すべての集合として、
$$ \mathrm{LocalBehavior}_{X,Y,x_0}\ :=\ \raise{0.2em}{\mathrm{LocalFns}_{X,Y,x_0}}\left/\raise{-0.2em}{\sim_{x_0}}\right. $$
と定める。
$f \sim_{x_0} g$というのがどういった状況なのかというと、$x_0$の周りの十分に狭い部分については$f$と$g$の挙動が完全に一致しているということです。
![この絵のなかの!FORMULA[158][37794][0]と!FORMULA[159][37825][0]は!FORMULA[160][36914495][0]で(より強く、!FORMULA[161][37329][0]上の任意の点で)局所的に同一](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FjjCoIcViiqJyunGGTxRz.png?alt=media) この絵のなかの$f$と$g$は$x_0$で(より強く、$W$上の任意の点で)局所的に同一
この絵のなかの$f$と$g$は$x_0$で(より強く、$W$上の任意の点で)局所的に同一
局所同一性はどれほどの範囲で$f$と$g$が一致しているのか、という情報を完全に無視しています。局所同一性で$\mathrm{LocalFns}_{X,Y,x_0}$を割ることで、$x_0$の周りの関数の局所的な挙動以外の情報、例えば、その関数がどれほど広い範囲で定義されうるものなのか、であったり、少し離れた場所での(その局所的な挙動の「元となった」)関数の挙動といった情報がすべて潰された同値類が得られます。
![少し離れたところでやんちゃな挙動をしても、何らかの開近傍の中での挙動さえ一致すれば局所同一。つまり、これらはすべて同じ同値類に属する関数たちで、同値類自体は!FORMULA[166][36914495][0]周りでの局所的な挙動がどのような感じなのかという情報しか持たない。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FtkD2zoWQHx62ugB4IyT7.png?alt=media) 少し離れたところでやんちゃな挙動をしても、何らかの開近傍の中での挙動さえ一致すれば局所同一。つまり、これらはすべて同じ同値類に属する関数たちで、同値類自体は$x_0$周りでの局所的な挙動がどのような感じなのかという情報しか持たない。
少し離れたところでやんちゃな挙動をしても、何らかの開近傍の中での挙動さえ一致すれば局所同一。つまり、これらはすべて同じ同値類に属する関数たちで、同値類自体は$x_0$周りでの局所的な挙動がどのような感じなのかという情報しか持たない。
このようにして取り出された関数の局所的な挙動のことを芽と呼びます。
$U \subseteq^\mathrm{open} X$、$x_0 \in U$と関数$f: U \rightarrow Y$が与えられたとき、同値類$[f]_{\sim_{x_0}} \in \mathrm{LocalBehavior}_{X, Y,x_0}$のことを$f$の$x_0$での芽(germ)と呼び、これを$\mathrm{germ}_{x_0}(f)$と書くこととする。
$V \subseteq^\mathrm{open} U \subseteq^\mathrm{open} X$、$x_0 \in V$と関数$f: U \rightarrow Y$が与えられたとき、$\mathrm{germ}_{x_0}(f) = \mathrm{germ}_{x_0}(f \upharpoonright_V)$。
$V$は$x_0$の開近傍であって$f \upharpoonright_V =(f \upharpoonright_V)\upharpoonright_V$であるから、$f \sim_{x_0} (f \upharpoonright_V)$であり、すなわち$\mathrm{germ}_{x_0}(f) = [f]_{\sim_{x_0}} = [f \upharpoonright_V]_{\sim_{x_0}} = \mathrm{germ}_{x_0}(f \upharpoonright_V)$。
芽は連続関数のみならず、任意の(開集合上に定義された)集合論的関数の局所的な動作というものを捉えるものになっています。「局所的な動作」の「局所的」という語彙は定義域側の局所性であり、芽を定義する上では、値域でどのように関数が挙動するかというところに制約を設ける必要が無いからです。したがって、例えば、ディリクレ関数のような至る所不連続な関数や、よりwildに、Conwayのbase-13関数のようなstrongly Darbouxな(i.e. グラフが$\mathbb{R}^2$内で稠密になる)関数についても、芽を考えることは(その行い単体で意義があるかはさておいて)できます。
実連続関数の層
元々、グラフを一挙に貼り合わせるというのがやりたかったことであり、グラフの各点に「局所的な挙動」をどう添加すればよいのか、という話を(正則関数という狭い関数クラスよりも広い)実連続関数たちに対しても一般化しようとして芽の概念がでてきた、というのがここまでの流れです。
つまり、各点であり得る実連続関数の芽というものを集めてくれば、実連続関数のグラフを貼り合わせたような空間が得られそうです。この考えを基に、次のように定義します。
集合$\left|\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}\right|$を
$$
\left|\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}\right|\ :=\
\bigsqcup_{x_0 \in \mathbb{R}}
\left\{ \mathrm{germ}_{x_0}(f) \in \mathrm{LocalBehavior}_{\mathbb{R},\mathbb{R},x_0} \;\middle|\; \text{$U \subseteq^\mathrm{open}\mathbb{R}$, $U \ni x_0$ で $f: U \rightarrow \mathbb{R}$ は連続} \right\}
$$
で定義する(ただし、$\bigsqcup$は直和(discriminated union))。$\left|\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}\right|$に、
$$
\biggl\{ \left\{ \left(x, \mathrm{germ}_{x}(f)\right) \;\middle|\; x \in U \right\} \;\bigg|\; \text{$U \subseteq^\mathrm{open}\mathbb{R}$ で $f: U \rightarrow \mathbb{R}$ は連続} \biggr\}
$$
を開基として生成した位相を入れた空間を$\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$と定義する。
開基の構成に着目してみると、$\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$の中では、芽が実連続関数$f: U_{\subseteq^\mathrm{open} \mathbb{R}} \rightarrow \mathbb{R}$に沿って開集合として繋がることで、$f$の「グラフ」、それも集合論的な$f$のグラフと比べてより情報を持っている、$x$と、$f$の$x$での芽の組の集まりとして表現されなおしたグラフそのものが開集合になっていることがわかります。特に、$V \subseteq U$な開集合を考えた時、$V$への$f$の制限を考えても$f\upharpoonright_V$は連続ですから、restriction-of-neighbourhood-in-germsを用いて$\left\{ \left(x, \mathrm{germ}_{x}(f)\right) \;\middle|\; x \in V \right\} = \left\{ \left(x, \mathrm{germ}_{x}(f \upharpoonright_V)\right) \;\middle|\; x \in V \right\} \subseteq^\mathrm{open} \mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$であることがわかります。つまり、$f$のグラフを、定義域の任意の開集合に沿って切り取ったものもやはり開になっています。
例として、$\mathrm{ReLU}=(x \in \mathbb{R})\mapsto \mathrm{max}(0, x)$ と $\mathrm{const}_0 = (x \in \mathbb{R})\mapsto 0$ の二つの関数を考えてみます。この時、例えば、$\left\{ \left(x, \mathrm{germ}_{x}(\mathrm{ReLU})\right) \;\middle|\; x \in (-2, 1) \right\}$と$\left\{ \left(x, \mathrm{germ}_{x}(\mathrm{const}_0)\right) \;\middle|\; x \in (-1, 2) \right\}$はいずれも$\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$で開です。
![!FORMULA[208][968379715][0]と!FORMULA[209][254702841][0]のグラフ(を開区間で切り取ったもの)に対応する、!FORMULA[210][352348446][0]の二つの開集合](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F0bcXCtiKigbQiwRrVRD8.png?alt=media) $\mathrm{ReLU}$と$\mathrm{const}_0$のグラフ(を開区間で切り取ったもの)に対応する、$\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$の二つの開集合
$\mathrm{ReLU}$と$\mathrm{const}_0$のグラフ(を開区間で切り取ったもの)に対応する、$\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$の二つの開集合
上図の中では$(0, \mathrm{germ}_0(\mathrm{ReLU}))$と$(0, \mathrm{germ}_0(\mathrm{const}_0))$が同じ原点の位置に描かれていますが、これらは$\left|\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}\right|$の異なる点であって、しかも、近傍による分離が不可能な(⁰ これら点をそれぞれ含む開近傍二つをどう取っても、それら開近傍が(¹ 特に、原点よりも負側の、$0$に貼りついている部分が重なることで ₁)空でない共通部分を持ってしまう ₀)二点になっています。このように、二つの部分的に一致していたグラフが途中から分岐する、といったことが$\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$では起こっており、これによって、$\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$はHausdorffではなくなっています。このHausdorff性の破れ方というのは、$\mathbb{R} \sqcup \mathbb{R}$の負の部分の半直線たちを(同じ負実数たちを同一視する、$\{(\mathrm{left}(x), \mathrm{right}(x)) \mid x \in \mathbb{R}_{<0}\}$の反射対称閉包$\mathrm{left}(\mathbb{R}_{<0})\sim\mathrm{right}(\mathbb{R}_{<0})$で割ることで)貼り合わせて得られる、二つの「原点」(だったもの)を持つ空間$\left(\raise{0.2em}{\mathbb{R} \sqcup \mathbb{R}}\left/\raise{-0.2em}{\mathrm{left}(\mathbb{R}_{<0})\sim\mathrm{right}(\mathbb{R}_{<0})}\right.\right)$がHausdorffでなくなる様子とよく似ています。
![商写像!FORMULA[221][-989060511][0]。原点が二つに分岐したままなのに、その任意の近傍の負側が貼り付いてしまっているせいで分離できない。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FMR8djWsVIRf4b8Vlf1bd.png?alt=media) 商写像$q: \mathbb{R} \sqcup \mathbb{R} \rightarrow \left(\raise{0.2em}{\mathbb{R} \sqcup \mathbb{R}}\left/\raise{-0.2em}{\mathrm{left}(\mathbb{R}_{<0})\sim\mathrm{right}(\mathbb{R}_{<0})}\right.\right) $。原点が二つに分岐したままなのに、その任意の近傍の負側が貼り付いてしまっているせいで分離できない。
商写像$q: \mathbb{R} \sqcup \mathbb{R} \rightarrow \left(\raise{0.2em}{\mathbb{R} \sqcup \mathbb{R}}\left/\raise{-0.2em}{\mathrm{left}(\mathbb{R}_{<0})\sim\mathrm{right}(\mathbb{R}_{<0})}\right.\right) $。原点が二つに分岐したままなのに、その任意の近傍の負側が貼り付いてしまっているせいで分離できない。
$\left|\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}\right|$と全く同じように、$z\in\mathbb{C}$とその開近傍で定義されている正則関数$U_{\subseteq^\mathrm{open} \mathbb{C}} \rightarrow \mathbb{C}$の芽の組をかき集めてくると、やはり、正則関数のグラフたちを重ね合わせたような空間が出てきます。
$$
\left|\mathcal{F}_\mathrm{holo}\right| := \bigsqcup_{z_0 \in \mathbb{C}}
\biggl\{ \mathrm{germ}_{z_0}(f) \in \mathrm{LocalBehavior}_{\mathbb{C},\mathbb{C},z_0} \;\bigg|\; \text{$U \subseteq^\mathrm{open}\mathbb{C}$, $U \ni z_0$ で $f: U \rightarrow \mathbb{C}$ は正則} \biggr\}
$$
に、
$$
\biggl\{ \left\{ \left(z, \mathrm{germ}_{z}(f)\right) \;\middle|\; z \in U \right\} \;\bigg|\; \text{$U \subseteq^\mathrm{open}\mathbb{C}$ で $f: U \rightarrow \mathbb{C}$ は正則} \biggr\}
$$
を開基として生成した位相を入れた空間を$\mathcal{F}_\mathrm{holo}$と定義する。
正則関数の範囲ではTaylor級数が開近傍上での挙動をちょうど記述できるので、芽と級数の係数列の間に全単射が作れます。つまり、芽の集まりとしての$\mathcal{F}_\mathrm{holo}$は、一番最初に仮置きしたnaive-defn-of-sheaf-of-holofnsでの$\mathcal{F}_\mathrm{holo}$と本質的には同じ集合になっています。そういった理由で、正則関数の層を、$z \in \mathbb{C}$と、その開近傍で定義された関数のTaylor級数の組を集めてきた空間だと考えていても問題はない、というわけです。
局所同相写像としての層
ここまでの話からして、点$(x_0, \mathrm{germ}_{x_0}(f)) \in \mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$というのは、$f$の集合論的グラフ$\mathrm{Graph}_f$の中の点$(x_0, f(x_0))$のように、グラフの一点を表現している(ただし、$(x_0, f(x_0))$周辺の$f$の挙動というのも同時に引き連れてきている)ようなものだったのでした。
グラフの一点は、その点が定義域のどの入力によってもたらされたのかという情報、即ち、XY平面に$\mathbb{R} \rightarrow \mathbb{R}$のグラフを描いたときの「X座標」を持っています。この情報を取り出す射影関数(projection)$p: \mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}} \rightarrow \mathbb{R}$を、$\left((x_0, \mathrm{germ}_{x_0}(f)) \in \mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}\right)\mapsto x_0$として定義します。
ここで一つのグラフ、例えば$f := (x \in (-1, 2)) \mapsto x^2 + 1$のグラフ$G_f := \{(x, \mathrm{germ}_x(f)) \mid x \in (-1, 2)\}$を考えてみます。すると、$p[G_f]$は(グラフをその定義域に射影するわけですから、当然)$(-1, 2)$になるわけですが、逆に、$x \in (-1, 2)$の$p$での原像は$G_f$の中には$(x, \mathrm{germ}_x(f))$のちょうどひとつしかないわけなので、$p \upharpoonright_{G_f} \;: G_f \rightarrow (-1, 2)$は全単射になっています。
![!FORMULA[249][421752348][0]を!FORMULA[250][38104][0]で射影する様子](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FI1rqIo6uIeshDdfBvDfh.png?alt=media) $G_f := \{(x, \mathrm{germ}_x(f)) \mid x \in (-1, 2)\}$を$p$で射影する様子
$G_f := \{(x, \mathrm{germ}_x(f)) \mid x \in (-1, 2)\}$を$p$で射影する様子
それどころか、(成り立つことそのものは絵を見れば直感的に明らかだと思いますが、)次も言えます。
$p \upharpoonright_{G_f} \;: G_f \rightarrow (-1, 2)$ は同相写像。
まず、$p \upharpoonright_{G_f} \;: G_f \rightarrow (-1, 2)$の連続性を示す。$U \subseteq^{\mathrm{open}} (-1, 2)$を任意に取ると、$p^{-1}[U] = \{ (x, \mathrm{germ}_x(f)) \mid x \in U \} = \{ (x, \mathrm{germ}_x(f \upharpoonright_U)) \mid x \in U \} $は$\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$の開基の元になっているから、$p^{-1}[U] \subseteq^\mathrm{open} \mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$。$p^{-1}[U] \subseteq G_f$なので$p^{-1}[U] \subseteq^\mathrm{open} G_f$。
$\left(p \upharpoonright_{G_f}\right)^{-1} \;: (-1, 2) \rightarrow G_f$の連続性を示せば終わり。そこで、$V \subseteq^{\mathrm{open}} G_f$を任意に取る。$G_f \subseteq^{\mathrm{open}} \mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$なので$V \subseteq^{\mathrm{open}} \mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$になっているから、$\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$の位相の定義より、$\mathbb{R}$の開集合と連続関数の組の族$\set{(U_i, f_i)}_{i \in I_V}$を用いて$V = \bigcup_{i \in I_V}\left\{ (x, \mathrm{germ}_x(f_i)) \mid x \in U_i \right\}$と書ける。各$i \in I_V$について$U_i \subseteq p[V] \subseteq (-1, 2)$だから、
$$
\begin{eqnarray}
\left(\left(p \upharpoonright_{G_f}\right)^{-1}\right)^{-1}[V]
&=& \left(p \upharpoonright_{G_f}\right)[V] \\
&=& \left(p \upharpoonright_{G_f}\right)\left[\bigcup_{i \in I_V}\left\{ (x, \mathrm{germ}_x(f_i)) \mid x \in U_i \right\}\right] \\
&=& \bigcup_{i \in I_V}\left(p \upharpoonright_{G_f}\right)\biggl[\bigl\{ (x, \mathrm{germ}_x(f_i)) \mid x \in U_i \bigr\}\biggr] \\
&=& \bigcup_{i \in I_V} U_i
\end{eqnarray}
$$
は$(-1, 2)$の開集合の和であり、開であることがわかる。
この証明は、$f$が具体的にどのような連続関数なのか、ということを一切用いていませんから、どんな連続関数$g : U_{\subseteq^\mathrm{open} \mathbb{R}} \rightarrow \mathbb{R}$を持ってきても同様に、射影をグラフ$G_g$に制限したものが同相写像になっていることが言えます。ですから、任意の$(x, \mathrm{germ}_x(f)) \in \mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$を取ってきたとき、芽の元となった関数のグラフ$G_f \subseteq \mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$はこの点の開近傍になっていて、しかも$p \upharpoonright_{G_f} \;: G_f \rightarrow (-1, 2)$が$\mathbb{R}$の開部分集合への同相写像を与えています。
このような性質をもつ連続写像のことを局所同相写像と呼びます。
$X, Y$を位相空間とする。連続写像$f: X \overset{\mathrm{cts}}{\rightarrow} Y$が局所同相写像(local homeomorphism)であるとは、任意の$x \in X$について開近傍$V_x \ni x$が存在して、$f$の$V_x$への制限$(f \upharpoonright_{V_x}): V_x \rightarrow f\left[V_x\right]$が同相写像になっており、$f[V_x] \subseteq^{\mathrm{open}} Y$なことである。
射影 $p: \mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}} \rightarrow \mathbb{R}$ は局所同相写像。
射影 $p: \mathcal{F}_\mathrm{holo} \rightarrow \mathbb{C} = (z_0, \mathrm{germ}_{z_0}(f)) \mapsto z_0$ は局所同相写像。
一般の位相空間上の層の定義
層とは、開集合上に定義された関数の芽を貼り合わせてグラフの重ね合わせを表現した$\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$のような位相空間であって、このような層の各点から芽を取る点への射影(例えば、先ほど見た$p: \mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}} \rightarrow \mathbb{R}$)が局所同相写像になるという話をここまで見てきました。
ここで少し話を飛躍させて、このように局所同相写像を取れる空間のことを層と呼びなおし、これを層の定義とすることにします。
$X$を位相空間とする。($X$上の)層(sheaf)とは、局所同相写像$p : \mathcal{F} \rightarrow X$のことである。$X$のことを($p$の)底空間、$\mathcal{F}$のことを($p$の)全空間と呼ぶ。
語の濫用として、$\mathcal{F} = \mathrm{dom}(p)$のことを$X$上の層と呼ぶこともある。
$\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$は$\mathbb{R}$上の層である。
$\mathcal{F}_\mathrm{holo}$は$\mathbb{C}$上の層である。
今までは連続関数すべてのグラフを一挙に重ね合わせるといった話をしてきていましたが、locally-homeo-sheafに従うと、例えば、ただ単に底空間をいくらか垂直に並べたような空間も層になっていることがすぐにわかります。
$X$を位相空間、$I$を集合とするとき、$\bigsqcup_I X$($X$の$|I|$個のコピー)から$X$への射影$p_I: \bigsqcup_I X \rightarrow X$は層になる。特に、$I = 0, 1$のときの空写像$p_0: \emptyset \rightarrow X$と、($\bigsqcup_1 X \cong X$という同一視のもとの)恒等写像$p_1: X \rightarrow X = \mathrm{id}_X$は層である。
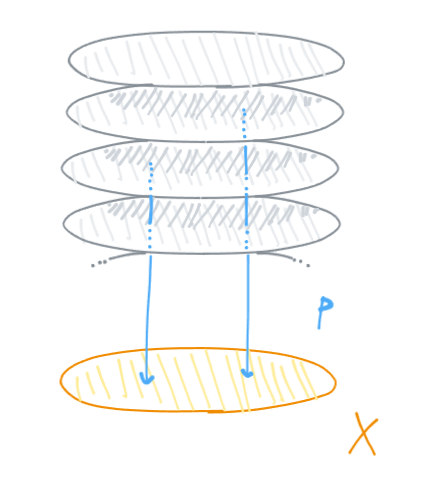 底空間のコピーを全空間とする層
底空間のコピーを全空間とする層
「いいやちょっとまて、(グラフの重ね合わせとしての)層に局所同相写像を取れるという話は分かったが、局所同相写像を取れるということだけを以てそれを層と呼ぶというのは、グラフの重ね合わせという概念をもはや捉えられなくなっているのではないか」、つまり「このように層を定義することで、グラフの重ね合わせ以外の空間も層になってきてしまうのではないか」、であったり「じゃあ、その$p_n: X^{\sqcup n} \rightarrow X$たちはどうグラフの重ね合わせなんだ」などと思われるかもしれません。これらは至極真っ当な疑問だと思います。
例えば、円環$S^1\times[0, 1]$を底空間として、その普遍被覆空間となる螺旋状の帯($\mathbb{R} \times [0, 1]$)からの射影$p: (x, j) \mapsto (e^{2 \pi ix}, j)$を考えます($S^1$は$\left\{\ z \in \mathbb{C} \;\big{|}\; |z| = 1\right\}$と定義されているものとします)。これも(より一般に、被覆写像は)局所同相写像であり層になっていますが、この構造のどこが関数のグラフの重ね合わせだと思えるのかは、直ちに明らかではありません(でも、ぐっと睨むとわかるかもしれません)。
![局所同相写像!FORMULA[320][-1372159183][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Fy5wd2DhwN7OfY5elUkZX.png?alt=media) 局所同相写像$p: \left(\mathbb{R} \times [0, 1]\right) \rightarrow \left(S^1 \times [0, 1]\right) = (x, j) \mapsto (e^{2 \pi ix}, j)$
局所同相写像$p: \left(\mathbb{R} \times [0, 1]\right) \rightarrow \left(S^1 \times [0, 1]\right) = (x, j) \mapsto (e^{2 \pi ix}, j)$
「わかるかもしれません」などと書いてあることから察することができたかもしれませんが、locally-homeo-sheafでの意味の層一般にも、「関数のグラフ」のような概念をふたたび見出すことができます。
$p: \mathcal{F} \rightarrow X$を$X$上の層として、$A \subseteq X$とする。$p$の$A$上の切断(section)とは、連続関数$f: A \rightarrow \mathcal{F}$であって、$(p \upharpoonright_{f[A]}) \circ f = \mathrm{id}_A$となるものである。
TakeuchiSCTは、「$p$の(開集合)$U$上の切断」のことを「$U$の上の$\mathcal{F}$の断面」と呼んでいます(そう呼びたい気持ちはわかる)。
![底空間!FORMULA[332][37360][0]の!FORMULA[333][37014873][0]個のコピーを全空間とする層の切断の例。連結開集合は同じコピーに飛んでいくが、異なる連結成分は別々のコピーに飛んでいくこともある。この例については、!FORMULA[334][36895][0]に離散位相を入れたものへの連続関数!FORMULA[335][388349475][0]の層になっていることがわかる。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F84oqtH7ub0Mv2ZcJArim.png?alt=media) 底空間$X$の$|I|$個のコピーを全空間とする層の切断の例。連結開集合は同じコピーに飛んでいくが、異なる連結成分は別々のコピーに飛んでいくこともある。この例については、$I$に離散位相を入れたものへの連続関数$U_{\subseteq^\mathrm{open} X} \rightarrow I$の層になっていることがわかる。
底空間$X$の$|I|$個のコピーを全空間とする層の切断の例。連結開集合は同じコピーに飛んでいくが、異なる連結成分は別々のコピーに飛んでいくこともある。この例については、$I$に離散位相を入れたものへの連続関数$U_{\subseteq^\mathrm{open} X} \rightarrow I$の層になっていることがわかる。
![局所同相写像!FORMULA[336][-1372159183][0]の切断の例。円環を3/4周ほどする領域を、「(!FORMULA[337][38104][0]で指定される)横方向」を変えないまま帯に貼り付けていくようなものになっている。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F4bSK3FbMXp6Kj0ai0pPn.png?alt=media) 局所同相写像$p: \left(\mathbb{R} \times [0, 1]\right) \rightarrow \left(S^1 \times [0, 1]\right) = (x, j) \mapsto (e^{2 \pi ix}, j)$の切断の例。円環を3/4周ほどする領域を、「($p$で指定される)横方向」を変えないまま帯に貼り付けていくようなものになっている。
局所同相写像$p: \left(\mathbb{R} \times [0, 1]\right) \rightarrow \left(S^1 \times [0, 1]\right) = (x, j) \mapsto (e^{2 \pi ix}, j)$の切断の例。円環を3/4周ほどする領域を、「($p$で指定される)横方向」を変えないまま帯に貼り付けていくようなものになっている。
例に描いた図のように$p: \mathcal{F} \rightarrow X$を「縦方向の射影」だと考えた時、$p$の切断というのは、「横方向の位置を動かさないまま、底空間の開集合を全空間に送る」ような連続関数です。気持ちとしては、全空間$\mathcal{F}$のことを、(横方向の)入力座標と、「その座標周辺で関数が取り得る局所的な挙動」の情報というのが各点に内包された「グラフを描く先の空間」だと捉えることができ、すると切断というのは、グラフを描く先の空間に($p(f(x)) = x$が要請するように入力座標を保ちながら)実際に点を打っていくような連続関数なのだと考えることができます。
このように考えると、$\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$を構成したときと同じように、切断の芽たちを切断に沿って開集合として繋ぎ合わせることで、「切断たちのグラフ」というのを一挙に貼り合わせて別の層を作ることができそうです。実際にそうすることができて、しかも、そうして作った層は元の層と「同じ」ものになります。つまり、局所同相写像$p: \mathcal{F} \rightarrow X$という一見素朴な構造があったとき、常に、これを$p$の切断$X \rightarrow \mathcal{F}$たちのグラフを貼り合わせた層だと考え直すということができます。
ここから先は、一連の定義と定理を以てこれを正当化することを目標とします。まずは、局所同相写像の切断の芽の空間を($\mathcal{F}_{\mathbb{R} \overset{\mathrm{cts}}{\rightharpoonup} \mathbb{R}}$などと同じような方法で)定義するところからはじめます。
$p: \mathcal{F} \rightarrow X$を層とする。集合
$$
\left|\mathcal{F}_{\mathrm{sects}(p)}\right| \;:=\;
\bigsqcup_{x_0 \in X} \left\{
\mathrm{germ}_{x_0}(f) \in \mathrm{LocalBehavior}_{X,\mathcal{F},x_0}
\;\bigg|\;
\text{$U \subseteq^\mathrm{open}X$, $U \ni x_0$ で $f: U \rightarrow \mathcal{F}$ は $p$ の切断}
\right\}
$$
に、
$$
\biggl\{
\left\{ \left(x, \mathrm{germ}_{x}(f)\right) \;\middle|\; x \in U \right\}
\;\bigg|\;
\text{$U \subseteq^\mathrm{open}X$ で $f: U \rightarrow \mathcal{F}$ は $p$ の切断}
\biggr\}
$$
を開基として生成した位相を入れた空間を$\mathcal{F}_{\mathrm{sects}(p)}$と定義する。
また、射影$p_{\mathrm{sects}(p)}: \mathcal{F}_{\mathrm{sects}(p)} \rightarrow X$を$(x, \mathrm{germ}_x(f)) \mapsto x$と定める。
$p: \mathcal{F} \rightarrow X$が層であるとき、射影$p_{\mathrm{sects}(p)}: \mathcal{F}_{\mathrm{sects}(p)} \rightarrow X$は連続。
$U \subseteq^\mathrm{open} X$を任意に取る。まず、全空間の定義から、
$$
\left(p_{\mathrm{sects}(p)}\right)^{-1}\left[U\right]
= \left\{ \left(x_0, \mathrm{germ}_{x_0}(f)\right) \;\big{|}\; \text{$x_0 \in U$, $V \subseteq^\mathrm{open} X$, $V \ni x_0$ で $f: V \rightarrow \mathcal{F}$ は $p$ の切断} \right\} \\
$$
と書ける。$p_{\mathrm{sects}(p)}$の連続性を示すためには、$\left(p_{\mathrm{sects}(p)}\right)^{-1}\left[U\right]$の要素$y$について、$y \in W \subseteq \left(p_{\mathrm{sects}(p)}\right)^{-1}\left[U\right]$となるような$y$の開近傍$W$を取れることを言えれば十分である。
そこで、$x_0 \in U$、$V \ni x_0$であるような$V \subseteq^\mathrm{open} X$、$p$の切断$f : V \rightarrow \mathcal{F}$を任意に取り、$\left(p_{\mathrm{sects}(p)}\right)^{-1}\left[U\right]$に包含される$\left(x_0, \mathrm{germ}_{x_0}(f)\right)$の開近傍を取れることを示す。まず、一般に切断の制限は切断であるから、$f \upharpoonright_{V \cap U}: (V \cap U) \rightarrow \mathcal{F}$は$p$の切断である。restriction-of-neighbourhood-in-germsより$\mathrm{germ}_{x_0}(f) = \mathrm{germ}_{x_0}(f \upharpoonright_{V \cap U})$なので、
$$
\begin{eqnarray}
\left(x_0, \mathrm{germ}_{x_0}(f)\right)
&=& \left(x_0, \mathrm{germ}_{x_0}(f \upharpoonright_{V \cap U}) \right) \\
&\in& \bigl\{ \left(x, \mathrm{germ}_x(f \upharpoonright_{V \cap U}) \right) \;\big{|}\; x \in V \cap U \bigr\}
\end{eqnarray}
$$
であるが、この右辺は(開基の元だから)開であって、かつ($p_{\mathrm{sects}(p)}$での像が$V \cap U$になっているから)$\left(p_{\mathrm{sects}(p)}\right)^{-1}\left[U\right]$に包含されている。
$p: \mathcal{F} \rightarrow X$を層、$U \subseteq^\mathrm{open}X$、$f: U \rightarrow \mathcal{F}$を$p$の切断とする。$f$の芽のグラフを$G_f := \{ (x, \mathrm{germ}_x(f)) \mid x \in U \} \subseteq^\mathrm{open} \mathcal{F}_{\mathrm{sects}(p)}$としたとき、$\left(p_{\mathrm{sects}(p)} \upharpoonright_{G_f}\right): G_f \rightarrow U$は同相写像。
各$x \in U$について$\left(p_{\mathrm{sects}(p)} \upharpoonright_{G_f}\right)^{-1}[\{x\}] = \{(x, \mathrm{germ}_x(f))\}$だから、$p_{\mathrm{sects}(p)} \upharpoonright_{G_f}$は全単射。
projection-from-space-of-germs-is-continuousにより$p_{\mathrm{sects}(p)} \upharpoonright_{G_f}$は連続だから、あとは$\left(p_{\mathrm{sects}(p)} \upharpoonright_{G_f}\right)^{-1} \;: U \rightarrow G_f$の連続性を示せばよい。そこで$V \subseteq^{\mathrm{open}} G_f$を任意に取る。まず、$G_f \subseteq^{\mathrm{open}} \mathcal{F}_{\mathrm{sects}(p)}$なので$V \subseteq^{\mathrm{open}} \mathcal{F}_{\mathrm{sects}(p)}$。よって、$\mathcal{F}_{\mathrm{sects}(p)}$の位相の定義より、$X$の開集合と$p$の切断の組の族$\set{(U_i, f_i)}_{i \in I_V}$を用いて$V = \bigcup_{i \in I_V}\left\{ (x, \mathrm{germ}_x(f_i)) \mid x \in U_i \right\}$と書ける。各$i \in I_V$について$U_i \subseteq \left(p_{\mathrm{sects}(p)}\right)[V] \subseteq U$だから、
$$
\begin{eqnarray}
\left(\left(p_{\mathrm{sects}(p)} \upharpoonright_{G_f}\right)^{-1}\right)^{-1}[V]
&=& \left(p_{\mathrm{sects}(p)} \upharpoonright_{G_f}\right)[V] \\
&=& \left(p_{\mathrm{sects}(p)} \upharpoonright_{G_f}\right)\left[\bigcup_{i \in I_V}\left\{ (x, \mathrm{germ}_x(f_i)) \mid x \in U_i \right\}\right] \\
&=& \bigcup_{i \in I_V}\left(p_{\mathrm{sects}(p)} \upharpoonright_{G_f}\right)\biggl[\bigl\{ (x, \mathrm{germ}_x(f_i)) \mid x \in U_i \bigr\}\biggr] \\
&=& \bigcup_{i \in I_V} U_i
\end{eqnarray}
$$
は$U$の開集合の和であり、開であることがわかる。
$p_{\mathrm{sects}(p)}: \mathcal{F}_{\mathrm{sects}(p)} \rightarrow X = (x, \mathrm{germ}_x(f)) \mapsto x$は局所同相写像。
$(x_0, \mathrm{germ}_{x_0}(f)) \in \mathcal{F}_{\mathrm{sects}(p)}$を任意に取り、$U := \mathrm{dom}(f) \subseteq^{\mathrm{open}} X$と書く。すると、
- $G_f = \{(x, \mathrm{germ}_x(f)) \mid x \in U\}$は$\mathcal{F}_{\mathrm{sects}(p)}$の開基の定義より$(x_0, \mathrm{germ}_{x_0}(f))$の開近傍になっており、
- $p_{\mathrm{sects}(p)}\left[G_f\right] = U \subseteq^\mathrm{open} X$、かつ
- local-homeomorphismness-of-graph-projectionより$\left(p_{\mathrm{sects}(p)} \upharpoonright_{G_f}\right): G_f \rightarrow U$は同相写像
であるから、$p_{\mathrm{sects}(p)}$は局所同相写像。
こうして作った層の切断の芽の層が元の層と(適切な意味で)「同じ」ものになるわけですが、それを示すために、層の切断に関する補題を二つ先に示しておきます。
一つ目の補題はlocal-homeomorphismness-of-graph-projectionと似た直感に基づくものです。
$p : \mathcal{F} \rightarrow X$を層、$f : U _{\subseteq^\mathrm{open} X} \rightarrow \mathcal{F}$を$p$の切断とすると、$f: U \rightarrow f[U]$は$p \upharpoonright_{f[U]}$の逆(連続)写像である。特に、$p \upharpoonright_{f[U]}: f[U] \rightarrow U$と$f: U \rightarrow f[U]$は共に同相写像であって、$f[U]$と$U$は同相。
$f$が$p$の切断であることから$\left(p \upharpoonright_{f[U]}\right) \circ f = \mathrm{id}_{U}$が言えるので、あとは$\mathrm{range}\left(p \upharpoonright_{f[U]}\right) \subseteq U$であることと$f \circ \left(p \upharpoonright_{f[U]}\right) = \mathrm{id}_{f[U]}$であることが言えればよい。
まず、$y \in f[U]$とすると、$x \in U$であって$f(x) = y$であるものが取れる。すると$\left(p \upharpoonright_{f[U]}\right)(y) = \left(p \upharpoonright_{f[U]}\right)(f(x)) = x \in U$であるから、$p \upharpoonright_{f[U]}: f[U] \rightarrow U$となっている。さらに、今の等式の両辺に$f$を適用すれば$\left(f \circ \left(p \upharpoonright_{f[U]}\right)\right)(y) = f(x) = y$が得られるが、$y \in f[U]$が任意だったから、結局$f \circ \left(p \upharpoonright_{f[U]}\right) = \mathrm{id}_{f[U]}$となる。
もう一つの補題は、局所同相性のおかげで切断の像が開になっているということを述べます。例えば、$\mathbb{R}^2$内の$(x \in (-1, 2)) \mapsto x^2 + 1$のグラフは$\mathbb{R}^2$内では開になっていないですが、これは$\mathbb{R}^2$が像の周りにべったりと貼り付いているから起こっている現象であって、局所同相性があるとこのような事態が起こらず、切断のグラフ一枚一枚が他から開集合で分離できるのだ、と言っているのだと思うことができます。
![!FORMULA[437][104314161][0]のグラフが!FORMULA[438][-207757014][0]内で開になれていない様子](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FIHUm5eCpkqJ0i0R4iWnM.png?alt=media) $(x \in (-1, 2)) \mapsto x^2 + 1$のグラフが$\mathbb{R}^2$内で開になれていない様子
$(x \in (-1, 2)) \mapsto x^2 + 1$のグラフが$\mathbb{R}^2$内で開になれていない様子
$p : \mathcal{F} \rightarrow X$を層、$f : U _{\subseteq^\mathrm{open} X} \rightarrow \mathcal{F}$を$p$の切断とすると、$f[U] \subseteq^\mathrm{open} \mathcal{F}$。
$f[U] \subseteq^\mathrm{open} \mathcal{F}$であることを示すには、各$y \in f[U]$について$y$の開近傍$W \subseteq^\mathrm{open} \mathcal{F}$であって$W \subseteq f[U]$なものが存在することを言えば十分である。
そこで、$y \in f[U]$を任意に取る。$p$が局所同相写像だから、$y$の開近傍$V_y \subseteq^\mathrm{open} \mathcal{F}$であって、$p[V_y] \subseteq^\mathrm{open} X$かつ$\left(p \upharpoonright_{V_y}\right): V_y \rightarrow p[V_y]$が同相写像になっているものが取れる。いま、$y \in f[U] \cap V_y \subseteq f[U]$であるから、あとは$f[U] \cap V_y$が$\mathcal{F}$で開になっていることを示せば良い。
$V_y \subseteq^\mathrm{open} \mathcal{F}$だから$f[U] \cap V_y \subseteq^\mathrm{open}f[U]$で、$f$の連続性より$f^{-1}[f[U] \cap V_y] \subseteq^\mathrm{open} U$。$U \subseteq^\mathrm{open} X$だったから$f^{-1}[f[U] \;\cap\;V_y] \subseteq^\mathrm{open} X$で、しかも補題8より$p[f[U] \;\cap\;V_y] = \left(p \upharpoonright_{f[U]}\right)[f[U] \;\cap\;V_y] = f^{-1}[f[U] \cap V_y] \subseteq^\mathrm{open} X$が言える。$p[f[U] \;\cap\;V_y] \subseteq p[V_y] \subseteq^\mathrm{open} X$であることから$p[f[U] \;\cap\;V_y] \subseteq^\mathrm{open} p[V_y]$だが、$(p \upharpoonright V_y)$が連続な単射であることから$f[U] \cap V_y \subseteq^\mathrm{open} V_y$。$V_y \subseteq^\mathrm{open} \mathcal{F}$だから、結局$f[U] \cap V_y \subseteq^\mathrm{open} \mathcal{F}$。
![全体の状況。黒 (!FORMULA[470][37360][0]) → 水色 (!FORMULA[471][37267][0]と!FORMULA[472][1127644163][0]) → 赤(!FORMULA[473][35903864][0]) → 紫 (!FORMULA[474][-654408161][0]とその!FORMULA[475][38104][0]での像) の順で描かれていると読むと良い。図のように、!FORMULA[476][35903864][0]として!FORMULA[477][1127644163][0]から途中で逸脱するようなものが取れてしまう場合もあるが、!FORMULA[478][1127644163][0]との共通部分は!FORMULA[479][-961625920][0]で開な!FORMULA[480][38383][0]の近傍になってくれている。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FvI54xjP4ZaxyFGwZBwAo.png?alt=media) 全体の状況。黒 ($X$) → 水色 ($U$と$f[U]$) → 赤($V_y$) → 紫 ($f[U] \cap V_y$とその$p$での像) の順で描かれていると読むと良い。図のように、$V_y$として$f[U]$から途中で逸脱するようなものが取れてしまう場合もあるが、$f[U]$との共通部分は$\mathcal{F}$で開な$y$の近傍になってくれている。
全体の状況。黒 ($X$) → 水色 ($U$と$f[U]$) → 赤($V_y$) → 紫 ($f[U] \cap V_y$とその$p$での像) の順で描かれていると読むと良い。図のように、$V_y$として$f[U]$から途中で逸脱するようなものが取れてしまう場合もあるが、$f[U]$との共通部分は$\mathcal{F}$で開な$y$の近傍になってくれている。
これで準備が整いました。元からある局所同相写像と、その局所同相写像の切断の芽を貼り合わせて作った「グラフの層」が実は同じ形をしているのだ、ということを述べます。
$p: \mathcal{F} \rightarrow X$を層とする。この時、同相写像$h: \mathcal{F} \rightarrow \mathcal{F}_{\mathrm{sects}(p)}$であって、$p_{\mathrm{sects}(p)} \circ h = p$となるものが取れる。
まずは$h: \mathcal{F} \rightarrow \mathcal{F}_{\mathrm{sects}(p)}$を構成する。$y \in \mathcal{F}$に対して、
$$
\mathcal{V}_y := \left\{ V \subseteq^\mathrm{open} \mathcal{F} \mid \text{$p\left[V\right] \subseteq^\mathrm{open}X$, $V \ni y$ かつ $(p \upharpoonright_{V}): V \rightarrow p\left[V\right]$ が同相写像} \right\}
$$
と定める。この時、$p$の局所同相性により取れる$y$の開近傍が$\mathcal{V}_y$の元であるから$\mathcal{V}_y \neq \emptyset$であり、その上、次が言える。
$H := (y \in \mathcal{F}) \mapsto \left\{\mathrm{germ}_{p(y)}\left(\left(p \upharpoonright_{V_y}\right)^{-1}\right) \;\middle|\; V_y \in \mathcal{V}_y \right\}$として、各$y \in \mathcal{F}$について$H(y)$の中に(主張1により)唯一存在する要素を$g_y$と定義する。$V_y \in \mathcal{V}_y$について$\left(p \upharpoonright_{V_y}\right)^{-1}: p\left[V_y\right] \rightarrow V_y$は$p$の$p\left[V_y\right]$上の切断であるから、$h(y) := \left(p(y), g_y\right)$と定義すれば$h: \mathcal{F} \rightarrow \mathcal{F}_{\mathrm{sects}(p)}$となる。すると、
$$
\begin{eqnarray}
(p_{\mathrm{sects}(p)} \circ h)(y)
&=& p_{\mathrm{sects}(p)}\left(\left(p(y), \mathrm{germ}_{p(y)}\left(\left(p \upharpoonright_{V_y}\right)^{-1}\right)\right)\right) \\
&=& p(y)
\end{eqnarray}
$$であるから$p_{\mathrm{sects}(p)} \circ h = p$で、あとは$h$が同相写像になっていることを示せば良い。
まずは、$h$が全単射であることを示す。これには、次の主張を示せば十分である。
まず、$f(x) \in h^{-1}[\{ (x, \mathrm{germ}_x(f)) \}]$を示す。補題8により$\left(p \upharpoonright_{f[U]}\right)^{-1} = f$で、さらに補題9と補題8から$f[U] \in \mathcal{V}_{f(x)}$であるから、主張1と併せて$$
\begin{eqnarray}
h(f(x))
&=& \left(p(f(x)), g_{f(x)}\right) \\
&=& \left(p(f(x)), \mathrm{germ}_{p(f(x))}\left(\left(p \upharpoonright_{f[U]}\right)^{-1}\right)\right) \\
&=& \left(x, \mathrm{germ}_{x}(f)\right)
\end{eqnarray}
$$
であることがわかる。
あとは$h^{-1}[\{ (x, \mathrm{germ}_x(f)) \}] \subseteq \{f(x)\}$を示せば良い。なので、$y \in h^{-1}[\{ (x, \mathrm{germ}_x(f)) \}]$を任意に取ることにする。すると、$p(y) = p_{\mathrm{sects}(p)}(h(y)) = p_{\mathrm{sects}(p)}((x, \mathrm{germ}_x(f))) = x$だから、$V_y \in \mathcal{V}_y$を適当に選べば、$$
\begin{eqnarray}
h(y)
&=& \left(p(y), g_{y}\right) \\
&=& \left(p(y), \mathrm{germ}_{p(y)}\left(\left(p \upharpoonright_{V_y}\right)^{-1}\right)\right) \\
&=& \left(x, \mathrm{germ}_{x}\left(\left(p \upharpoonright_{V_y}\right)^{-1}\right)\right) \\
\end{eqnarray}
$$
と書け、さらに、$\left(p \upharpoonright_{V_y}\right)$が全単射だから$y = \left(p \upharpoonright_{V_y}\right)^{-1}(x)$となっている。ところで、$y \in h^{-1}[\{ (x, \mathrm{germ}_x(f)) \}]$だったから、$\mathrm{germ}_{x}\left(\left(p \upharpoonright_{V_y}\right)^{-1}\right) = \mathrm{germ}_{x}(f)$となっている。つまり、$x$の開近傍$W \subseteq \mathrm{dom}\left(\left(p \upharpoonright_{V_y}\right)^{-1}\right) \cap \mathrm{dom}(f) = p[V_y] \cap U$があって$\left(p \upharpoonright_{V_y}\right)^{-1} \style{font-size:150%}{\upharpoonright}_W = f {\upharpoonright}_W$となっているわけだが、そうすると結局$y = \left(p \upharpoonright_{V_y}\right)^{-1}(x) = \left(\left(p \upharpoonright_{V_y}\right)^{-1} \style{font-size:150%}{\upharpoonright}_W\right)(x) = (f {\upharpoonright}_W)(x) = f(x)$なので良い。
次に、$h$の連続性を示す。これには終域の開基の任意の元の$h$での逆像が始域で開になっていることを示せば良いから、$U \subseteq^\mathrm{open}X$と$p$の切断$f: U \rightarrow \mathcal{F}$を任意に取り、$h^{-1}\left[\left\{ \left(x, \mathrm{germ}_{x}(f)\right) \;\middle|\; x \in U \right\}\right] \subseteq \mathcal{F}$が開であることを示す。しかし、主張2よりこの集合は$\left\{ f(x) \;\middle|\; x \in U \right\} = f[U]$であり、補題8よりこれは開。
最後に、$h^{-1}$の連続性を示す。そのため、$Y \subseteq^\mathrm{open} \mathcal{F}$と$y \in Y$を任意に取る。$f(y)$の開近傍$W \subseteq^\mathrm{open} \mathcal{F}_{\mathrm{sects}(p)}$であって$W \subseteq h[Y]$なものを取れることを示せば、$h[Y] \subseteq^\mathrm{open} \mathcal{F}_{\mathrm{sects}(p)}$であることが分かるので十分である。$V'_y \in \mathcal{V}_y$をひとつ取る。$V'_y \cap Y \subseteq^\mathrm{open} \mathcal{F}$で、一般に$\mathcal{V}_y$の要素の$y$との開近傍との共通部分は再び$\mathcal{V}_y$の要素となるから、$V_y := V'_y \cap Y \in \mathcal{V}_y$となる。任意の$y' \in V_y$について$V_y \in \mathcal{V}_{y'}$となっていることに注意すれば、
$$
\begin{eqnarray}
h[V_y]
&=&
\left\{
\left(p(y'), \mathrm{germ}_{p(y')}\left(\left(p \upharpoonright_{V_y}\right)^{-1}\right)\right)
\;\middle|\;
y' \in V_y
\right\} \\
&=&
\left\{
\left(x, \mathrm{germ}_x\left(\left(p \upharpoonright_{V_y}\right)^{-1}\right)\right)
\;\middle|\;
x \in p[V_y]
\right\}
\end{eqnarray}
$$となっていることがわかる。$\left(p \upharpoonright_{V_y}\right)^{-1}$が$p$の切断であり、かつ$p[V_y]$が開であったから、$h[V_y]$は$\mathcal{F}_{\mathrm{sects}(p)}$の開基の元であり、特に$h[V_y] \subseteq^\mathrm{open} \mathcal{F}_{\mathrm{sects}(p)}$である。$h(y) \in h[V_y] \subseteq h[Y]$であるから、$h^{-1}$の連続性は示された。
最後に、定理10から得られる$h: \mathcal{F} \rightarrow \mathcal{F}_{\mathrm{sects}(p)}$が満たす$p_{\mathrm{sects}(p)} \circ h = p$という条件が何なのか、というところの話を軽く述べておきます。ここまで関数空間の層の例、また、定理10までの一連の証明を通して見てきた通り、局所同相写像$p: \mathcal{F} \rightarrow X$というのは、各$y \in \mathcal{F}$について、$y \in \mathcal{F}$の原因となった切断への「入力座標」$x \in X$(i.e. 何らかの切断$f$について$f(x) = y$となるような$x$)を割り当てるような写像になっていました。この考え方で言えば、$p_{\mathrm{sects}(p)} \circ h = p$という条件は、「$h$が全空間の上下方向の値を入れ替えたりすることはあっても、入力座標方向には要素をずらすことがまったく無い」ということを述べています。
別の見方をすれば、$p$は層$\mathcal{F} \rightarrow X$を記述する唯一のデータとなっているわけで、$p_{\mathrm{sects}(p)} \circ h = p$というのは、「層$p$のことを層$p_{\mathrm{sects}(p)}$を用いて記述しなおすことができる」と主張しているとも考えることができます。これは代数系の準同型と似たようなことが起きており(例えば、$1 \mapsto ab$で定まる$\mathbb{Z} \rightarrow \langle a, b \;|\; \rangle$という群準同型は、$(ab)^n \in \langle a, b \;|\; \rangle$によって$n \in \mathbb{Z}$を記述しなおしているのだと思うことができます)、この等式のことを「$h$が$p \rightarrow p_{\mathrm{sects}(p)}$の『準同型』である」のだと読み取ることもできます。
実際、層$p_1: \mathcal{F}_1 \rightarrow X$から$p_2: \mathcal{F}_2 \rightarrow X$への射を、$h: \mathcal{F}_1 \rightarrow \mathcal{F}_2$であって$p_2 \circ h = p_1$であるようなものだと定義すると、層の射は圏を成します。この圏は$X$上のétale空間の圏と呼ばれています(nlab-etale-space)。定理10は、この圏の中で$\mathcal{F} \cong\mathcal{F}_{\mathrm{sects}(p)}$が成り立っていることを主張しているわけです。
![例えば、円環の被覆空間が二つ、!FORMULA[588][-207756983][0]に逆巻きに埋め込まれていたとして、「埋め込みの上下をひっくり返す」ような同相写像!FORMULA[589][37856][0]は射影を保つ。この!FORMULA[590][37856][0]は!FORMULA[591][36676198][0]から!FORMULA[592][36676229][0]への(可算無限個ある)射の一つとなっている。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F5cadLH5iHibb9gxVb9mB.png?alt=media) 例えば、円環の被覆空間が二つ、$\mathbb{R}^3$に逆巻きに埋め込まれていたとして、「埋め込みの上下をひっくり返す」ような同相写像$h$は射影を保つ。この$h$は$p_1$から$p_2$への(可算無限個ある)射の一つとなっている。
例えば、円環の被覆空間が二つ、$\mathbb{R}^3$に逆巻きに埋め込まれていたとして、「埋め込みの上下をひっくり返す」ような同相写像$h$は射影を保つ。この$h$は$p_1$から$p_2$への(可算無限個ある)射の一つとなっている。
以上です。