文献あり

ある行列と可換な行列はどのくらいあるか？

2665

はじめに

ある行列と可換な行列はどのくらいあるのでしょうか？定式化して言うと,
$A\in M_n( \mathbb{C} )$ について, 線型空間 $V_A:=\{B\in M_n( \mathbb{C} )\mid AB=BA\}$ の次元はどのくらいでしょうか？

実は, これは$A$のジョルダン標準形に現れるジョルダン細胞のサイズを用いて表せます.

対角成分$\lambda$, サイズ$k$のジョルダン細胞を$J(\lambda, k)$で表す.
$k_1\geq \cdots\geq k_r\geq 1$として, $A$のジョルダン標準形に現れるジョルダン細胞のうち対角成分が$\lambda$であるものが$J(\lambda, k_1), \cdots, J(\lambda, k_r)$であるとする. (各$k_i$および$r$は$\lambda$に依存する.)
このとき, $\dim V_A$は$\displaystyle\sum_{i=1}^r(2i-1)k_i$ を$A$の固有値$\lambda$ごとに足し合わせたものに等しい.

以下これを示します.

証明

基底の変換により$\dim V_A$は保たれるので, $A$をジョルダン標準形として考えてよい. $AB=BA$のとき$B$は$A$の広義固有空間を保つので, ある広義固有空間に注目して考察すればよい. 特に固有値$0$に対する広義固有空間を考えれば十分である.

すなわち, 示すべき命題は以下のものである.

$A$をべき零行列とし, $k_1\geq \cdots\geq k_r\geq 1$として, $A$のジョルダン標準形に現れるジョルダン細胞が$J(0, k_1), \cdots, J(0, k_r)$であるとしたときに
$$\dim V_A=\displaystyle\sum_{i=1}^r(2i-1)k_i . $$

$B\in V_A$を$A$のジョルダン細胞に沿ってブロック行列に区分けし, 各$ij$成分を$B_{ij}$とする. $B_{ij}$は$k_i\times k_j$行列である.

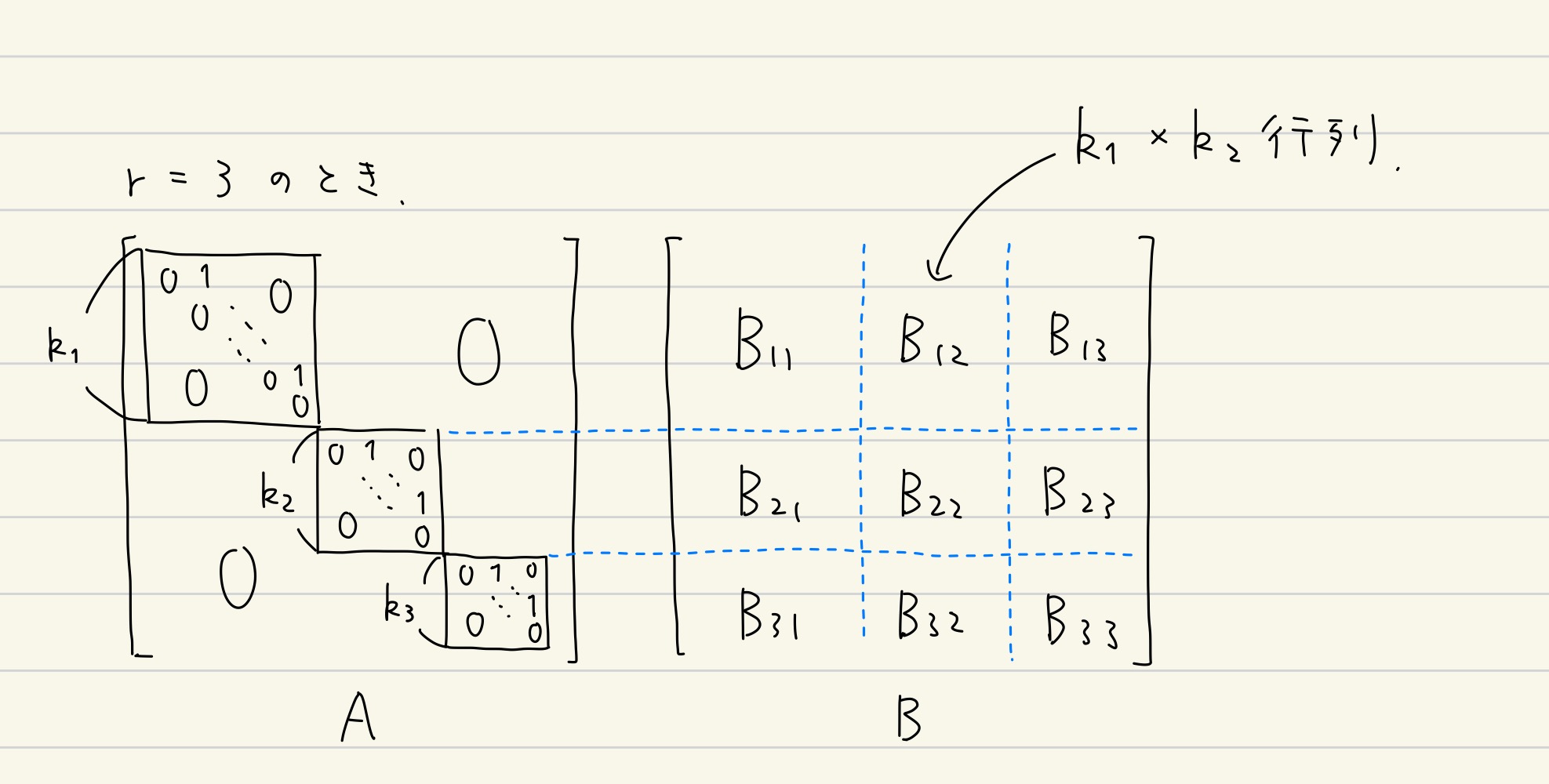ブロック行列の様子

$AB=BA$は, 各ブロック行列$B_{ij}$について $J(0, k_i)B_{ij}=B_{ij}J(0, k_j)$ が成立することと同値である.

計算の様子

この条件から$B_{ij}$の成分を直接計算して求めると次のようになる.(成分でおいて計算する様子は面倒だったので載せません...)

!FORMULA[38][-401040318][0]の表示 $B_{ij}$の表示

よって$B_{ij}$の自由度が$\min\{k_i, k_j\}$ なので, $B$全体の自由度(すなわち$V_A$の次元)は $\displaystyle\sum_{1\leq i, j\leq r}\min\{k_i, k_j\}$ に等しい. $k_i$が数えられる回数は$2i-1$回なので,
$\displaystyle\sum_{1\leq i, j\leq r}\min\{k_i, k_j\}= \sum_{i=1}^r (2i-1)k_i.$
以上より命題$2$が示されたので命題$1$が従う. (証明終)