ライツアウトパズルを使って単純無向グラフにおけるマッチングの総数の偶奇を求める方法を思いつきました

グラフ理論,ライツアウト,マッチング

160

はじめに

ある単純無向グラフ$G$が与えられたとき，$G$のマッチングの総数の偶奇を求める方法を見つけたので紹介します．

本文

定義

本記事で用いる定義です．

単純無向グラフ

頂点集合$V_G$, 辺集合$E_G\subseteq \{\{a,b\}\mid a,b\in V_G, a\neq b\}$の組を単純無向グラフとし，$G=(V_G,E_G)$で表す．

グラフ理論におけるマッチングの定義は以下の通りです．

マッチング

グラフ$G$におけるマッチングとは，集合$M_G\subseteq E_G$であって，$M_G$のどの$2$つの元も，互いに頂点を共有していないものである．

グラフ$G$におけるマッチングの総数は，トポロジカル・インデックス(細矢インデックス)という名前がついています．

トポロジカル・インデックス

$G$におけるトポロジカル・インデックス$Z_G$を以下で定義する．
$$Z_G=\sum_{k=0}^{n}\#M_{G,k}$$
ここで，$n$は$G$の頂点数であり，
$M_{G,k}$は$G$におけるマッチング$M_G$であって$\#M_G=k$であるもの全ての集合である．

主張

先に結論から述べてしまいます．

単純無向グラフ$G$の隣接行列を$A$とする．このとき，以下が成立する．
$$Z_G\equiv\det(A+I)\quad(\bmod2)$$

基本的に，$Z_G$そのものを求めるためには膨大な計算量を必要とするため，多項式時間では求めることができません(おそらく...というかそうじゃないとこの記事の意味がなくなるので困る)
しかし，この主張を用いることで$Z_G$の偶奇であれば$O(n^3)$で求めることができます．

ライツアウト

ライツアウトとは

いきなり何？となるかもしれないですが，ここで，ライツアウトパズルについて説明します．
見たことある人も多いと思います．正方形の盤面があり，各マスが白黒で着色されています．マスを$1$つ選んで操作を行うと，そのマスと，隣接しているマスの色が反転します，マスを上手く選び操作を施して，全てのマスの色を白色にするとクリアとなります．
ライツアウトの操作の例
このライツアウトですが，常に解くことができるわけではありません．
たとえば，$3\times3,7\times7$の盤面ではどの盤面からでもすべてのマスを白色にすることができるのですが，$4\times4,5\times5$の盤面では解けない配置が存在します．

ライツアウトの盤面を一般化する

単純無向グラフに色の情報を足したライツアウトグラフ(本記事独自の呼び方です)を以下のように定義します．

ライツアウトグラフ

頂点集合を$V_{G_L}$, 辺集合を$E_{G_L}\subseteq \{\{a,b\}\mid a,b\in V_{G_L}, a\neq b\}$とする．
また，関数$\mathrm{Col}_{G_L}:V_{G_L}\rightarrow\{0,1\}$によって$V_{G_L}$の各元が値を持っている．
このとき，ライツアウトグラフ$G_L$を$G_L=(V_{G_L},E_{G_L},\mathrm{Col}_{G_L})$で表す．
ライツアウトグラフ全体の集合を$\mathfrak{G}$とする．

ライツアウトグラフの各頂点に対する操作を次で定義します．

ライツアウトグラフの頂点に対する操作

また，$v\in V_{G_L}$について定まる関数$\mathrm{Swap}_v:\mathfrak{G}\rightarrow\mathfrak{G}$を以下で定義する．

$\mathrm{Swap}_v(G_L)=\mathrm{Swap}_v((V_{G_L},E_{G_L},\mathrm{Col}_{G_L}))=(V_{G_L},E_{G_L},\mathrm{Col}^*_{G_L})$
$\mathrm{Col}^*_{G_L}(v)=\begin{cases}0\quad\text{if }\ \mathrm{Col}_{G_L}(v)=1\\1\quad\text{otherwise}\end{cases}$
$\begin{aligned}\text{for each }u\in V_{G_L} &\text{ s.t. }u\neq v, \{u,v\}\in E_{G_L}:\\&\mathrm{Col}^*_{G_L}(u)=\begin{cases}0\quad\text{if }\ \mathrm{Col}_{G_L}(u)=1\\1\quad\text{otherwise}\end{cases}\end{aligned}$
$\text{for each }u\in V_{G_L}\text{ s.t. }u\neq v,\{u,v\}\not\in E_{G_L}:\mathrm{Col^*_{G_L}}(u)=\mathrm{Col_{G_L}}(u)$

長ったらしく書いていますが，要は$1$つ頂点を選んだら，その頂点自身と，頂点と隣接している頂点の$0,1$を入れ替えると言っているだけです．
この操作は適用させる順番は関係なく，同じ頂点へ$2$回操作することは操作していないことと同じです．まぁ当たり前ですね．
もう一つ，ライツアウトグラフの解も定義しておきます．

ライツアウトグラフの解

$\mathfrak{G}^*=\{(V,E,\mathrm{Col})\in\mathfrak{G}\mid \forall v\in V, \mathrm{Col}(v)=0\}$とする．このとき，
$X_{G_L}=\{v_i\mid 0\leq i\leq m \leq \#V_{G_L}, \mathrm{Swap}_{v_1}\circ\mathrm{Swap}_{v_2}\circ\cdots\mathrm{Swap}_{v_m}(G_L)\in\mathfrak{G}^*\}$を$G_L$における解とする．
ただし，条件を満たすような$v_1,v_2,\cdots v_m$が存在しないときは，$X_{G_L}=\varnothing$とし，$G_L$は解を持たないものとする.

すべての頂点の持つ値を$0$にできたら勝ちってことです．
ようやくライツアウトグラフについての定義がおわりました．
ライツアウトグラフの例を$1$つ載せます．
$$\begin{aligned} &G_L=(V_{G_L},E_{G_L},\mathrm{Col}_{G_L})\\ &V_{G_L}=\{1,2,3,4\},\ E_{G_L}=\{\{1,2\},\{2,3\},\{3,4\},\{3,1\}\},\\ &\mathrm{Col}_{G_L}(1)=0,\ \mathrm{Col}_{G_L}(2)=0,\\ &\mathrm{Col}_{G_L}(3)=1,\ \mathrm{Col}_{G_L}(4)=0 \end{aligned}$$
としてみます．
各頂点が持っている$\mathrm{Col}_{G_L}$の値について$0$を白，$1$を黒にして描画します．
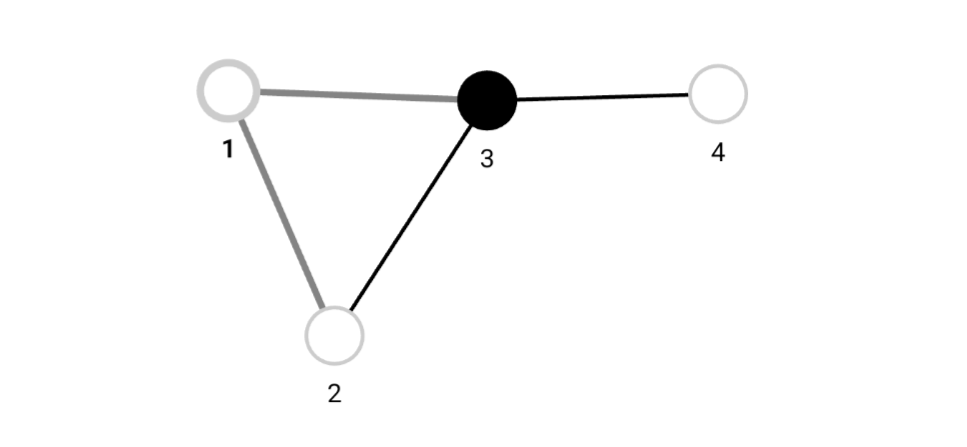ライツアウトグラフの例
この場合の$G_L$における解は存在して，$X_{G_L}=\{1,3,4\}$です．
正方形の盤面におけるライツアウトの自然な拡張となっていると思います．
グラフ版のライツアウトパズルの簡易的なエディタを作成しましたので載せておきます．興味のある人は触ってみるとちょっと楽しいかもしれないです．
グラフ版ライツアウト

ライツアウトグラフが常に解を持つかの判定

$G_L\in\mathfrak{G}$について，$G_L=(V_{G_L},E_{G_L},\mathrm{Col}_{G_L})$ とします．このとき，$\mathrm{Col}_{G_L}$の値の組み合わせの違いとして考えられる $2^{\#V_{G_L}}$個のライツアウトグラフの集合を$G_L^*$とします．
$G^*_L$の要素の中には，少なくとも$1$つは解をもつようなものが存在することは自明でしょうが，$V_{G_L},E_{G_L}$によっては，$G^*_L$の要素すべてが解を持っているような場合もあります．
与えられたライツアウトグラフが，頂点の持っている値にかかわらず常に解を持っているための条件を求めてみましょう．
ここからの演算は特に断りのない限り，$\mathbb{F}_2$上で行います．
また，簡単のため，$G_L$の頂点数を$n:=\#V_{G_L}$とします．
$G_L$の各頂点について，$\mathrm{Col}_{G_L}(v_i)$の値を並べた$n$次ベクトルを考え，このベクトルを$\overrightarrow{G_L}$とします．
また，$\mathrm{Swap}_{v_i}$も同じように，色を変える頂点に対応する成分を$1$，それ以外を$0$とすれば，$n$次ベクトルが作れます．このベクトルを$\overrightarrow{S_{v_i}}$とします．
すると，$\overrightarrow{G_L}+\overrightarrow{S_{v_i}}$によって得られるベクトルも，$\mathrm{Swap}_{v_i}(G_L)$の各頂点における$\mathrm{Col}_{\mathrm{Swap}_{v_i}(G_L)}$の値を並べた$n$次ベクトルとなっています．
このことから，連立方程式
$$\overrightarrow{G_L}+\sum_{i=1}^{n}x_i\overrightarrow{S_{v_i}}=\vec{0}$$
を，未知数$x_1,x_2,\cdots,x_n$について解くことで，ライツアウトグラフの解を求めることができます．
また，この連立方程式が解を持たなければ，ライツアウトグラフの解は常に存在するとは言えないため，与えられたライツアウトグラフが，頂点の持っている値にかかわらず常に解を持っているための条件は，
$$\det(S)=1$$
となります．ただし，$S$は$\overrightarrow{S_{v_1}},\overrightarrow{S_{v_2}},\cdots,\overrightarrow{S_{v_n}}$を並べた$n$次正方行列です．
隣り合う頂点に対応する成分を$1$にしていたため，$S$は対称行列となります．
先ほど例に挙げたグラフで考えてみます．
$$\overrightarrow{G_L}=\begin{pmatrix}0\\0\\1\\0\end{pmatrix}, \overrightarrow{S_{1}}=\begin{pmatrix}1\\1\\1\\0\end{pmatrix},\overrightarrow{S_{2}}=\begin{pmatrix}1\\1\\1\\0\end{pmatrix},\overrightarrow{S_{3}}=\begin{pmatrix}1\\1\\1\\1\end{pmatrix},\overrightarrow{S_{4}}=\begin{pmatrix}0\\0\\1\\1\end{pmatrix}$$
であるため，
$$S=\begin{pmatrix}1&1&1&0\\1&1&1&0\\1&1&1&1\\0&0&1&1\end{pmatrix}$$
です．この行列は$G_L$の隣接行列に単位行列を足したものです．
また，$G_L$のすべての頂点に$1$つずつループを付加したグラフの隣接行列としてみることもできます．
ここで，$\det(S)$の定義を思い出します．$\mathbb{F}_2$で考えていたので，置換の符号は無視してよく，
$$\det(S)=\mathrm{perm}(S)=\sum_{\sigma\in\mathfrak{S}}\prod_{i=1}^{n}S(i,\sigma(i))$$
です．ただし，$\mathfrak{S}$を$n$次対称群，$S$の$(i,j)$成分を$S(i,j)$としました．
行列式は，$S$の成分から$1$を選んでかけるような置換の選び方の個数として解釈できます．
さらに，$S$は対称行列であり，対角成分について非対称な成分の選び方は偶数個存在します．
したがって，対角成分について対称な成分の選び方のみをカウントすればよいです．

マッチングとライツアウト

マッチングの話に戻ります．先ほど例に挙げたライツアウトグラフと同じ頂点と辺の組を持つ単純無向グラフ$G$を例として話します．
$$\begin{aligned} &G=(V_G,E_G)\\ &V_G=\{1,2,3,4\},\ E_G=\{\{1,2\},\{2,3\},\{3,4\},\{3,1\}\} \end{aligned}$$
ここで，$G$のマッチング$M_G$を
$$M_G=\{\{1,2\},\{3,4\}\}$$
とします．この辺を赤く着色して次に示します．
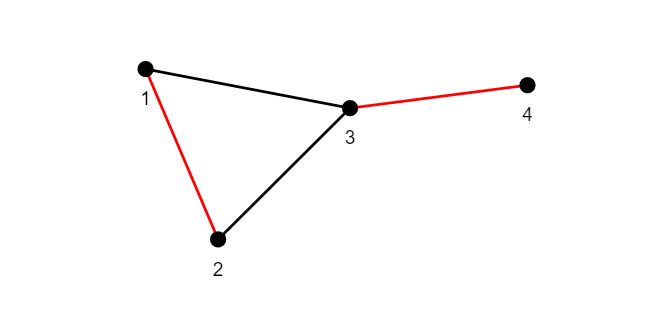マッチングの一例
$M_G$の各要素について，辺で結ばれている頂点の組を入れ替えるように置換$\sigma$を定めます．
この例だと
$$\sigma=\begin{pmatrix}1&2&3&4\\2&1&4&3\end{pmatrix}$$
です．この置換によってえらばれる$S$の要素は
$$ S=\begin{pmatrix}1&\color{red}{1}&1&0\\\color{red}{1}&1&1&0\\1&1&1&\color{red}{1}\\0&0&\color{red}{1}&1\end{pmatrix} $$
であり，対角成分について対称な選び方となっています．
一般に，各$M_G$に対して，異なる$\sigma$が定まり，それらは全て対角成分について対称な選び方を与える置換となります．
逆に，対角成分について対称な選び方を与える$\sigma$それぞれに対して，異なる$M_G$が定まります．
したがって，
$$\det(S)=\#\bigcup M_G=Z_G$$
です．
$G$の隣接行列を$A$とすると，$S=A+I$であったため，冒頭の主張である
$$Z_G\equiv\det(A+I)\quad(\bmod2)$$
が示せました．