～同値類と群の準同型定理について。～

この記事では、同値類という用語を初めて見る人向けに同値類とは何かを端的にイメージ重視で解説します。その関連として群の準同型定理についても、線型写像を少し知っている人向けに解説します。

本題

　集合$S$があって、$S$は$S=A_{1}\cup A_{2}\cup A_{3}...$かつ、各$i,j\in\mathbb{N}$について $A_{i}\cap A_{j}=\varnothing$という風に、お互いに交わらない部分集合$A_{1}, A_{2},A_{3}...$達に分割されているとする（これを直和分割と言う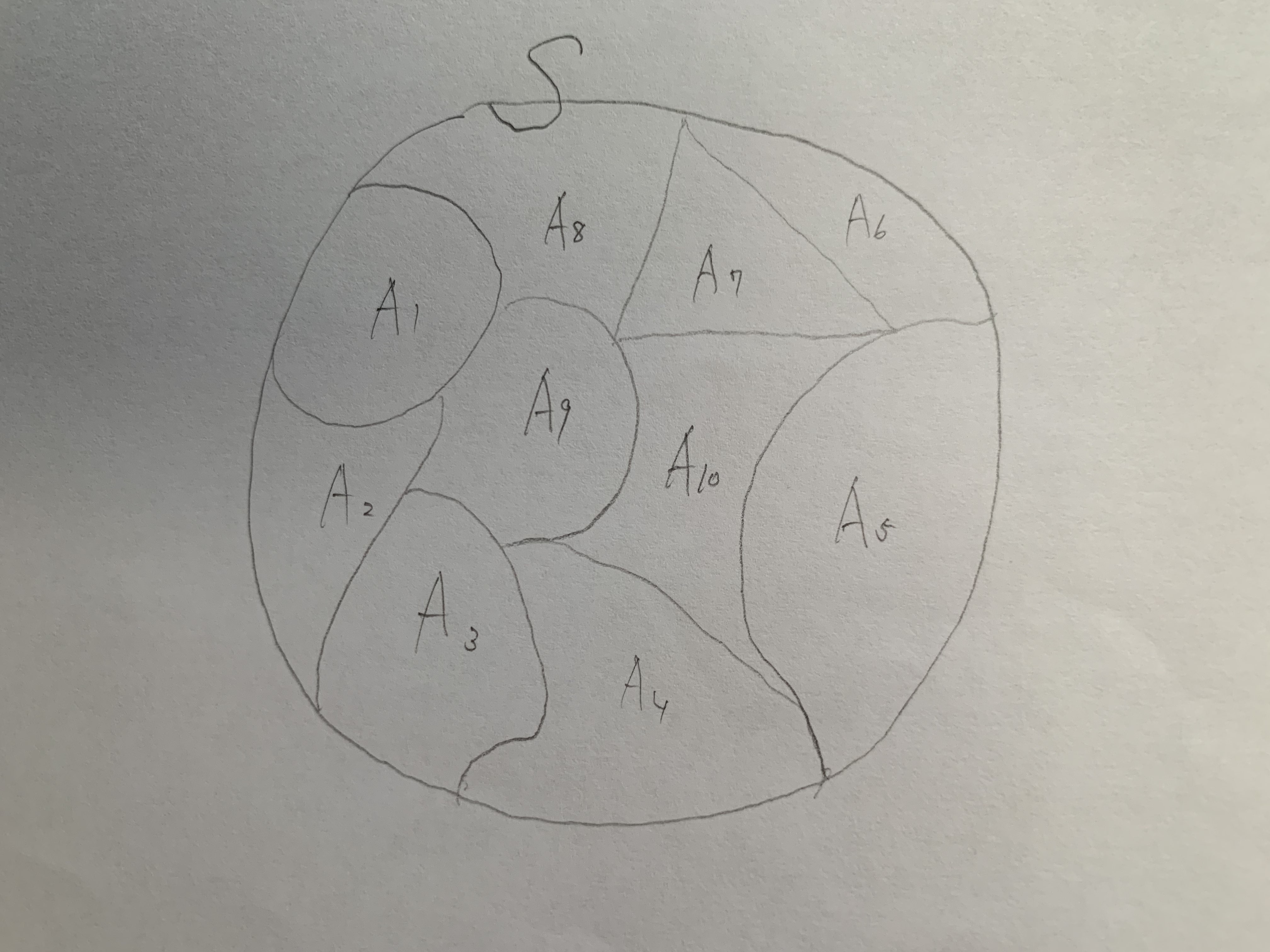）。 直和分割
この時、

イメージ的には何か集まりSがあった時に、その集まりS内でさらに$A_{1}, A_{2},A_{3}...$という風に分類する時の、同じ分類に分けられた物同士の集まりが同値類です。同じ値を持つ類（たぐい）の者達です。
例１　学校の全校生徒を学年別にクラス分けする時の各クラス、例えば2年Aや3年B組などはそれぞれ同値類2年A組、同値類3年B組と言う。学年別で分けた時には同値類は１年と２年と３年の３つ（ただし３学年あるとする）。
例2　所属するサークルで分類する場合は、兼部が可能であれば同値類は無い。改めて兼部不可能な部活達（例えばAとBとC）とその他の部に所属する人で分類し直せば、同値類はAとBとCとその他の人達の４つ。
例３　$S$を正の整数、$n$を何か自然数とする。$S$の中から$n$で割り算した時の余りが等しくなる様な数を集めた時、これは直和分割出来ていて同値類は$n$個ある（あまりが0~n-1のn個）。

同値類の性質

　ここでは同値類に含まれる元同士の関係について考えます。それは一言に同じ分割に属する点同士の関係と言えて（上の例では同じクラスメート・同級生・差が$n$の倍数同士等）、その、同じ分割に属するという事を定式化します。
手順（i）
　各$A_{i}$の元を書き下すと、$\lbrace x\in S \space \vert \space x\in A_{i}かつx\notin A_{j},i\neq j\rbrace $（条件式の後半部分は仮に元々例２の様な分類がされている状況も考えて書いていますがあまり気にしなくても大丈夫です）こう書ける。
もしもある$x^{1},x^{2}\in S$が両方共にある$A_{i}$に属していて（$x^{1},x^{2}\in A_{i}$）　、なおかつ$x^{2},x^{3}\in S$が$x^{2},x^{3}\in A_{j}$とする。
この時、$x^{2}$は異なる同値類に属する事は無いため$A_{j}=A_{i}$という事になる。よって$x^{2},x^{3}\in A_{i}$
手順（ii）
　（i）の流れを数学の記号を使って整理する。
「$x^{1},x^{2}$が同じ同値類に属する事」を$x^{1}\sim x^{2}$と書く。したがって「$x^{2},x^{3}$が同じ同値類に属する事」は$x^{2}\sim x^{3}$と書かれる。この記法では、（i）の論理は
$x^{1}\sim x^{2}$かつ$x^{2}\sim x^{3}$ならば$x^{1}\sim x^{3}$
と整理される。ちなみにこの事を推移律を満たすと言う。
また次の事が成り立つ。
$x^{1}\sim x^{1}$（反射律）
$x^{1}\sim x^{2}$ならば$x^{2}\sim x^{1}$（対称律）
　つまり

　～を同じ同値類に属する事ではなく、もっと一般的に、何らかの評価基準で同じ分類に振り分けられる時に$x^{1}\sim x^{2}$等と書く事にする。

同値関係について

　つまり、同値関係は直和分割を作り、直和分割は同値関係を作るという事。

例４　例１と例３は同値関係で分類している。例２の改めた方の分け方は同値関係をなしている。
例５　実数空間$R^{n}$（$n=3$等）において点$x^{i}$と$x^{j}$が原点対称な位置関係にある時に$x^{i}\sim x^{j}$と書くとすると、～の意味する関係性は同値関係ではない。
証明　$x\in (R^{n}-\lbrace 原点0 \rbrace)$の原点対称な点は$-x$なので$x\nsim x$。▯
ちなみに$x^{i}\sim x^{j}$となる点は$x^{i}= x^{j}=$原点0に限るため、$x^{i}\sim x^{j}$ならば、$x^{i}= x^{j}=$原点0なため、$x^{j}\sim x^{i}$で対称律を満たし、同様に推移律も満たす。
例６（大小関係）実数の集合$R^{1}$において、$x^{i}$と$x^{j}$が$x^{i}\geq x^{j}$な時に$x^{i}\sim x^{j}$と書くとすると、～の意味する関係性は同値関係ではない。　
証明　$x\in R^{1}$として、$x\geq x$（等号成立）なため$x\sim x$で反射律はOK。$x^{i}\geq x^{j}$ならば$x^{j}\geq x^{i}$になるのは$x^{i}=x^{j}$な場合に限る為、一般的には成り立たないので対称律を満たさない。推移律に関しては$x^{i}\geq x^{j}$かつ$x^{j}\geq x^{k}$ならば$x^{i}\geq x^{j}$なため成り立つ。▯
ちなみに、$R^{1}$の部分集合を各実数１つだけを元に持つ集合$\lbrace x \rbrace $で定義して、$R^{1}=\bigcup_{x= -∞}^∞\lbrace x\rbrace $とすると、各同値類$\lbrace x\rbrace$内にてこの大小関係$\geq$は同値関係になる。しかし、この同値分割は$R$の元を大小関係$\geq$によって分類した結果作られる分割ではなく、$\geq$に関して反射律・対称律・推移律を満たす様に分類したら出来る分割。この時の同値関係とは$\geq$を同値関係にする様な元同士の関係。

群の準同型定理について

ここでの目的は次の

これを順を追って説明する事です。
まずはベクトル空間の線型写像の場合の計算をして、そのまま同じ計算方法で群の準同型の場合に当てはめる様に進めます。

ベクトル空間の線型写像の場合

$A,B$を実ベクトル空間、$λ,ν\in R$、$a_{i},a_{j}\in A$とする。

例７　１次函数の比例式$y=ax$や多変数函数$f(x_{1},x_{2},x_{3},...)=x_{1}x_{2}x_{3}...$は線型写像。後者は多重線型関数と言われ、各$x_{i}$に関して線型性を持っている。各変数をスカラー倍する事は、ベクトル空間の点をスカラー倍する事とは別物なので注意。同様にベクトル空間の２点の和ベクトルを$f$で計算する事と、その２点での$f$の２つの値の和を計算する事は別物であり等しくないので注意（実際に分配法則で計算してみると計算結果が等しくない）。

$e_B$を$B$の単位元（ゼロベクトル）とする。

例８　Aの単位元（ゼロベクトル）$e_A$は$e_A\in \operatorname{Kerf}$。$f$が全射な時は$\operatorname{Imf}=B$。

証明　※群の場合との計算に対応付けるため、少し遠回りな計算手順を踏みます。
$k_i,k_j\in \operatorname{Kerf}$、$λ_i,λ_j\in R$とする。
・まずは和とスカラー倍について閉じている事、つまり$k_i+k_j\in \operatorname{Kerf}$と$λk\in \operatorname{Kerf}$を示す。
$f(λ_ik_i+λ_jk_j)=λ_if(k_i)+λ_jf(k_j)=0$
よって和とスカラー倍で閉じている。
・単位元は$A$のゼロベクトル$e_A$。実際、$f(e_A)+f(e_A)=f(e_A+e_A)=f(e_A)$より$f(e_A)=e_B$なため$e_A\in Kerf$であって、$e_A+x=x$が成り立っている。
・$x\in \operatorname{Kerf}$の$A$としての逆元$-x$に関して。$f(-x)+f(x)=f(-x+x)=f(e_A)=e_B$より$f(-x)=-f(x)$であり、この右辺は$=-e_B=e_B$（e_Bはゼロベクトル）なため$-x\in \operatorname{Kerf}$
・スカラー係数との結合法則や分配法則等も$A$からそのまま引き継がれる。　▯

つまり$\operatorname{Kerf}$は$A$の部分空間という事。例えば$R^{3}$では、部分空間とは無限に広がる平面や無限に伸びる直線の事。$R^{3}$そのものや$\lbrace 原点 \rbrace$も部分空間。

～$A$に同値関係を導入する。～

$a_i,a_j\in A$に関して、$a_j-a_i\in \operatorname{Kerf}$を満たす時に$a_i\sim a_j$と書く。

例９（図を参照）例えば$R^{3}$に$\operatorname{Kerf}$の２次元平面が広がっているのをイメージすると、$\operatorname{Kerf}$内で直交する２つの単位ベクトルを用意して、$\operatorname{Kerf}$に直交する単位ベクトルを１つ用意した時のこの３つを基本ベクトルとする正規直交座標系を作った時（図の$e_1,e_2,e_3$）、平面$\operatorname{Kerf}$に直交する軸（図の$e_3軸$）の方向の成分が等しい時に$\sim$を書くという事。例えばある点xがあり、$x\sim y$な$y$全体（図の平面$\lbrack x \rbrack$）は、$x$を含み、$\operatorname{Kerf}$に平行な２次元平面をなす。 例９の図
実際には手前にも横にも無限に広がっている。また、$Kerf$は原点を含み$Kerf=\lbrack 0 \rbrack$

この時、

証明
反射律・・・$a-a=0=e_A\in \operatorname{Kerf}$よって$a\sim a$
対称律・・・$a_j-a_i\in \operatorname{Kerf}$ならば$a_i-a_j=-(a_j-a_i)\in \operatorname{Kerf}$よって$a_i\sim a_j\Longrightarrow a_j\sim a_i$
推移律・・・、$a_j-a_i\in \operatorname{Kerf}$かつ、$a_k-a_j\in \operatorname{Kerf}$ならば、$a_k-a_i=(a_k-a_j)+(a_j-a_i)\in \operatorname{Kerf}$よって$a_i\sim a_j$かつ$a_j\sim a_k\Longrightarrow a_i\sim a_k$　▯
例１０（図を参照）　$R^3$内において２次元部分空間Cがあるとして、Cの各点に直交する直線（$R^1$）が交わっているとすると、これはCの各点を通る$R^1$達に直和分割されており、この時の同値関係は「Cの同じ点の延長線上にある時に～を書く」という事になる。言い換えれば、平面Cと、Cに直交する直線上のベクトルで正規直交座標系（図の$e_1,e_2,e_3$）を作った時に、C平面の成分（２次元方向の成分）が等しければ～を書くという事で、数式で書けば$a_i\sim a_j\Longleftrightarrow a_j-a_i\in R^1$。仮に$Kerf$が１次元の直線な場合はこういう直和分割になる。 例１０の図
Cの垂線で原点を通るものが$Kerf=\lbrack 0 \rbrack$

　～による同値分割の同値類で、ある$a\in A$を含むものを$\lbrack a \rbrack$と書く。

証明　$a_i\sim a$（$a_i-a\in \operatorname{Kerf}$）なため、各$a_i$に対して$k_i\in \operatorname{Kerf}$が存在して、$a_i=a+k_i$と書ける。
$f(a_i)=f(a+k_i)=f(a)+f(k_i)=f(a)$　▯

証明 $\lbrack a_i \rbrack$と$\lbrack a_j\rbrack$との和を$\lbrack a_i+a_j\rbrack$で定義したい。その為には、$\lbrack a_i \rbrack$内の他の点$a'_i$と、同様に別の点$a'_j\in \lbrack a_j \rbrack$を使って和を$\lbrack a'_i+a'_j\rbrack$で計算した時にこの２つが等しくなって$\lbrack a_i+a_j\rbrack=\lbrack a'_i+a'_j\rbrack$が成り立つ様にしたい。何故なら、もしも等しくならなければそれは同じ２元$\lbrack a_i \rbrack$と$\lbrack a_j\rbrack$の和に関して計算結果が２通り以上存在する事を意味するため。
　実際に$\lbrack a_i+a_j\rbrack=\lbrack a'_i+a'_j\rbrack$を示す。記号は補題６と同じにする。
$a'_i+a'_j=a_i+k_i+a_j+k_j$
より、$f(a'_i+a'_j)=f(a_i+k_i+a_j+k_j)=f(a_i)+f(k_i)+f(a_j)+f(k_j)=f(a_i+a_j)$
なため、系から$\lbrack a_i+a_j\rbrack=\lbrack a'_i+a'_j\rbrack$が言える。
　次に、この和に対してベクトル空間を成す事を示す。
単位元（ゼロベクトル）は$\lbrack e_A \rbrack=Kerf$。実際に$\lbrack e_A \rbrack+\lbrack a \rbrack=\lbrack e_A+a \rbrack=\lbrack a \rbrack $が全ての$a\in A$について成り立つ。
$e_A$を$-a$で置き換えれば、$\lbrack a \rbrack$の逆元（逆ベクトル）は、$\lbrack -a \rbrack$。
同様にベクトル空間Aと計算が同じなため、演算が閉じている事やスカラー係数との結合法則や分配法則についてはAの性質をそのまま引き継ぐ。
したがってこの和に対して同値類の集合はベクトル空間をなす。▯

例１１例９の図では、同値類の集合とは$e_3$軸の事とほぼ同じ。つまり１次元ベクトル空間$R^1$。例１０の図では同値類の集合とは平面Cの事とほぼ同じ。つまり２次元ベクトル空間$R^2$。
例えば、同じ平面が直線的に積み重なっていて、その積み上がる方向が１次元的な事だとか（例９）、直線の分布が平面Cに沿って２次元的に存在している（例１０）という様にイメージすると分かり易いかもしれません。

証明　単位元は$f(0)$。
$λ_if(a_i)+λ_jf(a_j)=f(λ_ia_i+λ_ja_j)\in \operatorname{Imf}$より和とスカラー倍について閉じている。
スカラーとの結合法則や分配法則はBからそのまま受け継ぐ。
よって$Imf$は$B$の部分ベクトル空間。▯

　$Imf$を新たにBと置くか、もしくは$f$は全射な線型写像とする。

証明　前半は系で書いた事なので、最後の線型同型を誘導する事を証明する。
同値類の集合のベクトル空間をA/～と記し、$\hat f:A/～→\operatorname{Imf}$を$\hat f(\lbrack a\rbrack):=f(a)$で定義すると、$\hat f$が線型同型写像な事が次の様に示される。
$\hat f$の全単射性・・・$f$は全射なため$B=\operatorname{Imf}$の各点で原像が存在して、系によってそれらはそれぞれA/～の１点（１つの同値類）ずつに対応している。
$\hat f$の線型性・・・$f$は線型写像なため$\hat f(λ_i\lbrack a_i\rbrack +λ_j\lbrack a_j\rbrack)=f(λ_ia_i+λ_ja_j)=λ_if(a_i)+λ_jf(a_j)=λ_i\hat f(\lbrack a_i\rbrack)+λ_j\hat f(\lbrack a_i\rbrack)$よって線型写像。▯

群の場合

上のベクトル空間の場合と同じ論理で命題３が導けます。
最初は群の定義と準同型写像の定義から。

各$g_i\in G$とする。

上の定義は、ベクトル空間の様な演算法則をもう少し抽象化したものだと思ってもらいたいです。

証明　略。▯

GとG'を群とする。演算・は略記として、$g_1・g_2=g_1g_2$等と書く。

線型写像との違いは、係数という概念が無い事と、演算を和＋で行っていない事。例えば正則行列の全体は行列の積について群を成すけど、この積は積の順番が可換ではない。しかしこの記事で準同型定理を示すためには、計算的には係数を全て１にするだけで大丈夫。可換性も使っていない。

G'の単位元を$e'$と書く。

証明　略。▯

群$G$に同値関係を入れる。
$x,y\in G\Longrightarrow x^{-1}y\in \operatorname{Kerf}$な時、$x\sim y$と書く。これは同値関係。
この時の同値類の集合を$G/～$と書く。

証明　略。核を使って上記の様な同値関係を定めると$G/～$は群を成す。▯

証明　略。▯