QとQ-{0}は位相同型

$A,B$を$\R$の稠密部分集合とし，$f\colon A\to B$を順序同型写像とする．$f$が位相同型写像でもあることを示す．$a\in A$と$\varepsilon>0$を任意にとる．$B$は稠密であるから，
$$\ex b\in B,\;0< f(a)-b<\varepsilon$$

$f$は全単射であるから，
$$\ex a'\in A,\;f(a')=b$$
このとき$0< f(a)-f(a')$であり$f$は順序同型なので$a'< a$である．$a'< x< a$について，
$$0< f(a)-f(x)< f(a)-f(a')<\varepsilon$$
が成り立つ．よって$f$は連続である．$A$と$B$を入れ替えれば$f^{-1}$も連続である．

したがって$f$は位相同型写像である．

$h_{a,b}^{c,d}$は全単射であり，正数倍拡大と平行移動の組合せなので順序を保つ．

$\Q$と$\Q\setminus\{0\}$は共に$\R$の稠密部分集合であるから，補題1より順序同型$f\colon\Q\setminus\{0\}\to\Q$を構成すればよい．そのために順序同型$f_+\colon\Q_{>0}\to\Q_{>\sqrt2}$を構成する．

$$\Q_{>0}=(0,1]_\Q\sqcup \Q_{>1}$$
$$\Q_{>\sqrt{2}}=(\sqrt{2},2]_\Q\sqcup\Q_{>2} $$
と非交和分解できることに注意する．
まず順序同型$f_0\colon(0,1]_\Q\to(\sqrt2,2]_\Q$を構成する．

\begin{align} (0,1]_\Q &=\bigsqcup_{j=0}^\infty(\fr{1}{j+2},\fr{1}{j+1}]_\Q\\ &=\cdots\sqcup(\fr{1}{3},\fr{1}{2}]_\Q\sqcup(\fr{1}{2},1]_\Q \end{align}

\begin{align} (\sqrt{2},2]_\Q &=\bigsqcup_{j=0}^\infty(\fr{\lceil 10^{j+1}\sqrt{2}\rceil}{10^{j+1}},\fr{\lceil 10^j\sqrt{2}\rceil}{10^j}]_\Q\\ &=\cdots\sqcup(1.415,1.42]_\Q\sqcup(1.42,1.5]_\Q\sqcup(1.5,2]_\Q \end{align}
と非交和分解する．補題2によって各区間ごとに順序同型$g_j$を
$$g_j:=h_{\fr{1}{j+2},\fr{1}{j+1}}^{\fr{\lceil 10^{j+1}\sqrt{2}\rceil}{10^{j+1}},\fr{\lceil 10^j\sqrt{2}\rceil}{10^j}}\colon(\fr{1}{j+2},\fr{1}{j+1}]_\Q\to (\fr{\lceil 10^{j+1}\sqrt{2}\rceil}{10^{j+1}},\fr{\lceil 10^j\sqrt{2}\rceil}{10^j}]_\Q$$
で定めることができ，順序同型
$$f_0:=\bigsqcup_{j=0}^\infty{g_j}\colon(0,1]_\Q\to(\sqrt2,2]_\Q$$
が得られる．

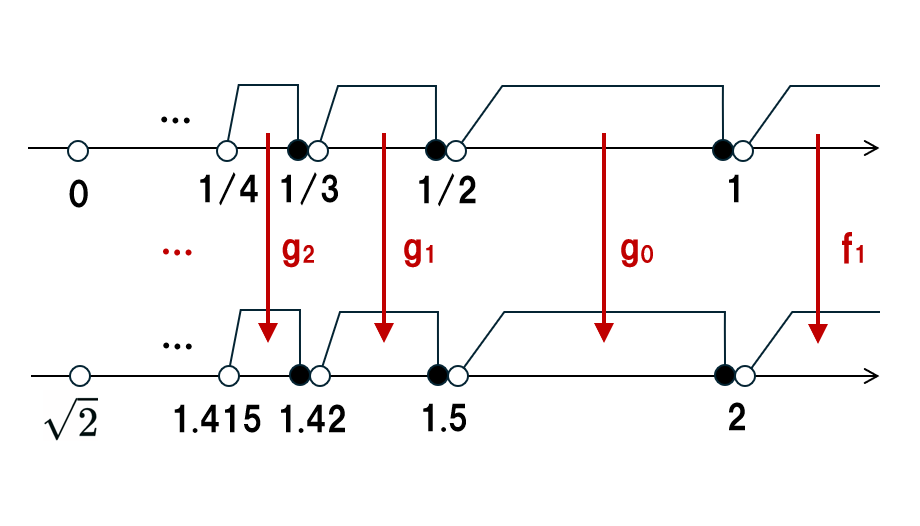
また，
$$f_1\colon\Q_{>1}\to\Q_{>2},\ x\mapsto2x$$
と定めるとこれは順序同型である．よって順序同型
$$f_+:=f_0\sqcup f_1\colon\Q_{>0}\to\Q_{>\sqrt2}$$
が得られる．さらに
$$f_{-}\colon\Q_{<0}\to\Q_{<-\sqrt2},\ x\mapsto -f_+(-x)$$
で定めるとこれも順序同型である．そこで
$$\Q\setminus\{0\}=\Q_{<0}\sqcup\Q_{>0}$$
$$\Q=\Q_{<\sqrt{2}}\sqcup\Q_{>\sqrt{2}}$$
という非交和分解に注意して，
$$f:=f_{-}\sqcup f_{+}\colon \Q\setminus\{0\}\to\Q$$
とおけば，これは求める順序同型である．