テトリスの代数と素因数分解の一意性
目次
- はじめに
- 動機
- 挿入について
- 素因数分解とその一意性
- 外挿入について
- 最後に
はじめに
この記事では$\mathbb{N}$の冪集合$\mathcal{P}(\mathbb{N})$上の挿入演算についてまとめます。これは、テトリスにおける消去可能性問題を研究する中で出てきたものです。テトリスとの関係は次節「動機」で解説します。
また、今回扱う代数系では素因数分解のような分解が可能です。この記事ではこれを正に素因数分解と呼ぶべき理由の一つを解説します。
今回は全ての証明を省略する。
以下、この記事では$\mathbb{N}=\{0,1,2,\dots\},\mathbb{N}_{>0}=\mathbb{N}^+=\{1,2,3,\dots\}$とし、
自然数$n$と言った場合は、$n\in\mathbb{N}$を指すものとする。
動機
テトリスでは、次の画像のように、ある列が「消去」されることが本質的である。
列が消去される様子
これを数学的に表現するために、まずブロックに以下のように名前をつける。
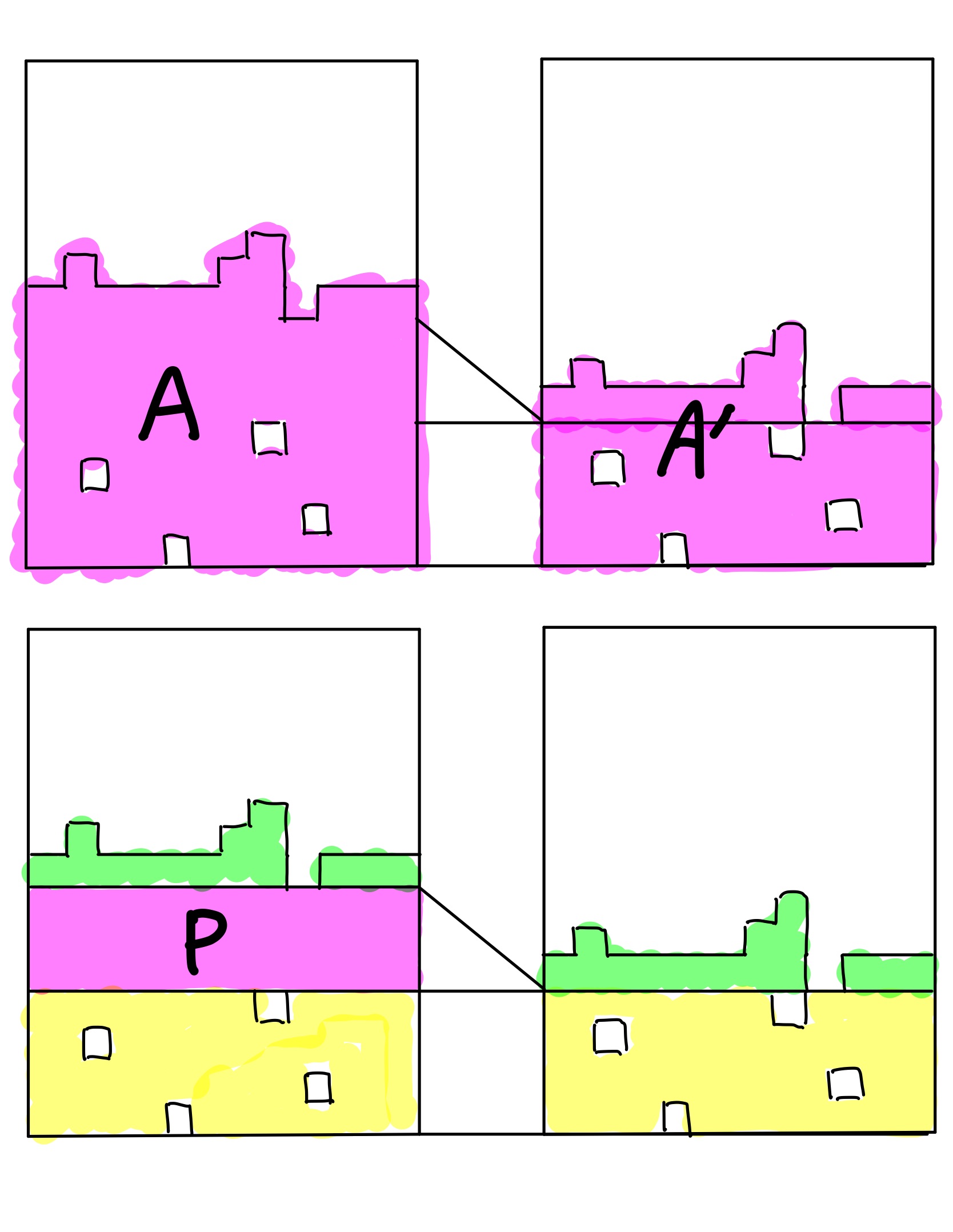各ブロックの名前
この図では$A$のうち$P$の部分が「消去」されて$A'$となっている。
ここで、発想を転換させて、「$A'$に$P$を挿入することで$A$となる」と見ることにする。
すると、後述する「挿入演算」によって、$A=A'\circ P$と表現することができる。
これによって、挿入の逆演算として「消去」を定式化できる、ということになる。
そのために、まずは最も単純な、横幅が$1$のテトリス盤面である$\mathbb{N}$とその冪集合$\mathcal{P}(\mathbb{N})$上の挿入演算について考察する。
挿入について
$\mathcal{P}=\mathcal{P}(\mathbb{N})=2^\mathbb{N}\stackrel{\mathrm{def}}{=}\{A|A\subset\mathbb{N}\}$
$\mathcal{F}=\mathcal{F}(\mathbb{N})\stackrel{\mathrm{def}}{=}\{A\in\mathcal{P}(\mathbb{N})||A|<\infty\}$
$\mathcal{G}=\mathcal{G}(\mathbb{N})\stackrel{\mathrm{def}}{=}\{A\in\mathcal{P}(\mathbb{N})||A^c|=\infty\}$
$\mathcal{P}$は$\mathbb{N}$の冪集合、$\mathcal{F}$は$\mathcal{P}$の有限集合全体、$\mathcal{G}$は$\mathcal{P}$の補無限集合全体である。
また$\mathcal{P}-\mathcal{F}$は無限集合全体、$\mathcal{P}-\mathcal{G}$は補有限集合全体である。
これらは$\mathcal{F}\subset\mathcal{G}\subset\mathcal{P}$を満たす。
$A \subset \mathbb{N}$を補無限集合、つまり$A\in\mathcal{G}(\mathbb{N})$とする。
このとき、$\varphi_A:\mathbb{N} \rightarrow \mathbb{N} - A $なる順序同型が一意に存在する。この$\varphi_A$の終域を$\mathbb{N}$に延長した順序単射も再び$\varphi_A$と書き、これを$A$が誘導する挿入写像という。
この挿入写像により、挿入演算が以下のように定義される。
$A,B\in\mathcal{G}(\mathbb{N})$のとき、$\varphi_B\circ\varphi_A=\varphi_C$をみたす$C\in\mathcal{G}(\mathbb{N})$が一意的に存在する。
このとき、$C=A\circ B$と書き、これを$A$への$B$の挿入という。
次は非常に重要な定理である。
$(\mathcal{G}(\mathbb{N}),\circ,\varnothing)$はモノイドをなす。つまり、以下が成り立つ。
- 任意の$A,B,C\in\mathcal{G}(\mathbb{N})$に対して、$(A\circ B)\circ C=A\circ(B\circ C)$
- 任意の$A\in\mathcal{G}(\mathbb{N})$に対して、$A\circ\varnothing=\varnothing\circ A=A$
一般に、写像の合成は非可換なので、$\mathcal{G}$は非可換モノイドとなる。
また、$\varnothing\in\mathcal{G}(\mathbb{N})$であることに注意せよ。
素因数分解とその一意性
以下は、素因数分解とその一意性を考える上で基本的である。
$\mathcal{F}(\mathbb{N})$は$\mathcal{G}(\mathbb{N})$の部分モノイドである。
以下、$\mathcal{F}(\mathbb{N})$上で、昇順標準形と降順標準形の二種類の標準形を定義する。特に、後者は素因数分解ともいい、$\mathcal{F}(\mathbb{N})$及び$\mathcal{G}(\mathbb{N})$の構造を調べるのに重要な役割を果たす。
$n\in\mathbb{N}$に対して、
$(n)\stackrel{\mathrm{def}}{=}\{n\}\in\mathcal{G}(\mathbb{N})$
つまり、$\mathbb{N}$の一元集合$\{n\}\in\mathcal{G}(\mathbb{N})$を$(n)$と書くのである。
$A=\{a_0,\dots,a_n\}\in\mathcal{F}(\mathbb{N})$かつ$a_0<\dots< a_n$のとき、
$A＝(a_0)\circ\dots\circ(a_n)$
となる。この表示を$A$の昇順標準形という。
$n\in\mathbb{N},m\in\mathbb{N}$に対して、
$(n)^m\stackrel{\mathrm{def}}{=}\stackrel{\mathrm{m個}}{(n)\circ\dots\circ(n)}$
とする。ただし、$m=0$のときは、
$(n)^m=(n)^0\stackrel{\mathrm{def}}{=}\varnothing$
と定める。
$A\in\mathcal{F}(\mathbb{N})$に対して、$|A|=n<\infty$とするとき、
ある自然数列$\{e_k\}_{k=0}^n\subset\mathbb{N}$が一意に存在し、
$A=(n)^{e_n}\circ\dots\circ(0)^{e_0}$
となる。この表示を、降順標準形または素因数分解という。
昇順標準形と降順標準形は、混乱のない場合にはどちらも単に標準形と呼ぶこともあるということをここで注意しておく。
$A\in\mathcal{F}(\mathbb{N})$の降順標準形を、$A=(n)^{e_n}\circ\dots\circ(0)^{e_0}$とするとき、
$e_n+\dots+e_0=|A|$
となる。
$A\in\mathcal{F}(\mathbb{N})$に対して、$|A|=n<\infty$とするとき、
$n< m$なる任意の$m\in\mathbb{N}$に対して、ある自然数列$\{e_k\}_{k=0}^m\subset\mathbb{N}$が一意に存在し、
$A=(m)^{e_m}\circ\dots\circ(0)^{e_0}$
となり、$e_m=\dots=e_{n+1}=0$であり、$e_n,\dots,e_0$は標準形の指数と一致する。
この表示もまた、降順標準形あるいは素因数分解という。
また、降順標準形を素因数分解と呼ぶ理由は、形式が類似しているという点以外にも本質的な点があることを次節で解説する。
外挿入について
ここでは、降順標準形を素因数分解と見るべき理由の一つを見ていく。
結論から述べると、降順標準形は$\mathcal{F}(\mathbb{N})$と$\mathbb{N}_{>0}$の間の同型を与えるからである。
これを見ていくために、新たに外挿入という演算を定義する。
$A,B\in\mathcal{F}(\mathbb{N})$に対し、$n=\max\{|A|,|B|\}$とし、$A,B$の降順標準形をそれぞれ、
$A=(n)^{e_n}\circ\dots\circ(0)^{e_0}$
$B=(n)^{d_n}\circ\dots\circ(0)^{d_0}$
とするとき、$A$と$B$の外挿入$A\bullet B$を以下で定める。すなわち、
$A\bullet B\stackrel{\mathrm{def}}{=}(n)^{e_n+d_n}\circ\dots\circ(0)^{e_0+d_0}$
$p_0,p_1,p_2,p_3,\dots$を素数を小さい順に並べた自然数数列$2,3,5,7,\dots$とする。
$(\mathcal{F}(\mathbb{N}),\bullet,\varnothing)$は可換モノイドをなす。つまり、以下が成り立つ。
- 任意の$A,B,C\in\mathcal{F}(\mathbb{N})$に対して、$(A\bullet B)\bullet C=A\bullet(B\bullet C)$
- 任意の$A\in\mathcal{F}(\mathbb{N})$に対して、$A\bullet\varnothing=\varnothing\bullet A=A$
- 任意の$A,B\in\mathcal{F}(\mathbb{N})$に対して、$A\bullet B=B\bullet A$
$(\mathcal{F}(\mathbb{N}),\bullet,\varnothing)$と$(\mathbb{N}_{>0},\times,1)$はモノイドとして同型。
実際、$A\in\mathcal{F}(\mathbb{N})$に対し、$A$の降順標準形を$A=(n)^{e_n}\circ\dots\circ(0)^{e_0}$とするとき、
$p(A)=p((n)^{e_n}\circ\dots\circ(0)^{e_0})=p_n^{e_n}\times\dots\times p_0^{e_0}$
なる写像$p:\mathcal{F}(\mathbb{N})\rightarrow \mathbb{N}_{>0}$はモノイド同型を与える。
つまり、降順標準形は自然数の素因数分解と同一視されるのである。
最後に
振り返り
今回は、$\mathcal{G}(\mathbb{N})$上の挿入演算を定め、その部分モノイド$\mathcal{F}(\mathbb{N})$上で二種類の標準形が存在することを見た。また、降順標準形を用いて外挿入を定め、これにより$\mathcal{F}(\mathbb{N})$と$\mathbb{N}_{>0}$が同型であることを見た。
実は...
実は、今回定義した挿入演算は左項が$\mathcal{P}(\mathbb{N})$に延長することができる。
また、二種類の標準形及び外挿入$\bullet$は、$\mathcal{P}(\mathbb{N})$の有限集合全体$\mathcal{F}(\mathbb{N})$でのみならず、$\mathcal{G}(\mathbb{N})$において定義することもできる（！）
だが、無限集合に関する標準形は無限積表示ということであるから、収束概念が必要となってくるので、適切な位相を導入せねばならない。
次回予告
次回以降は演算の定義域を拡張するのと、位相を導入し、収束について議論するところからである。（位相空間論の知識は不要）
(実は標準形は$\mathcal{P}(\mathbb{N})$全域でも定義できます!)
この記事を高評価した人
この記事に送られたバッジ
投稿者
