院解15 京大数学系 H24 数学I 5 積分で定義された複素関数の微分

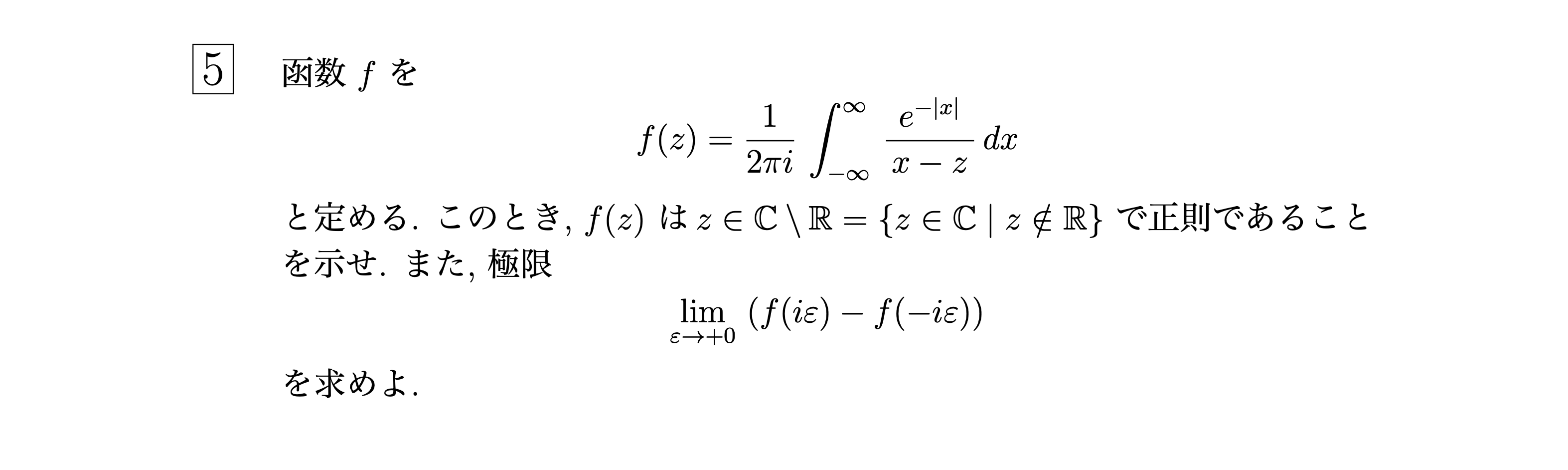
$\displaystyle \int_{-\infty}^\infty \left | \dfrac{e^{-|x|}}{x-z}\right|dx\leq\displaystyle \int_{-\infty}^\infty \left | \dfrac{e^{-|x|}}{\text{Im}z}\right|dx<\infty$であり,絶対収束しているのでルベーグ積分であるとして考える.スカラー倍で正則性は変わらないから,平行移動により$z$は純虚数であるとして示せば十分である.そこで,$z=ib$,$b\in\mathbb{R}\backslash\{0\}$とおく.すると
$\dfrac{f(z+h)-f(z)}{h}=\dfrac{1}{2\pi h i}\displaystyle\int_{-\infty}^\infty \left( \dfrac{e^{-|x|}}{x-ib-h}-\dfrac{e^{-|x|}}{x-ib}\right)dx$
$=\dfrac{1}{2\pi i}\displaystyle\int_{-\infty}^\infty \dfrac{e^{-|x|}}{(x-ib-h)(x-ib)}dx$,ここで$|b-h|<\dfrac{|b|}{2}$のとき
$\dfrac{1}{2\pi }\left| \dfrac{e^{-|x|}}{(x-ib-h)(x-ib)}\right|\leq \dfrac{1}{2\pi}\dfrac{2e^{-|x|}}{|b|^2}$であり,この右辺が可積分であることからLebesgueの収束定理を用いることができ
$\dfrac{f(z+h)-f(z)}{h}\to \dfrac{1}{2\pi i}\displaystyle\int_{-\infty}^\infty \dfrac{e^{-|x|}}{(x-ib)^2}dx$,($h\to 0$).よって$\mathbb{C}\backslash \mathbb{R}$で$f(z)$は正則である.

次に,被積分関数は$x$についての偶関数だから
$f(i\epsilon )-f(-i\epsilon)=\dfrac{1}{i\pi}\displaystyle\int_{-\infty}^\infty \dfrac{e^{-x}}{x^2+\epsilon^2}dx=\dfrac{2}{i\pi}\displaystyle\int_{0}^\infty \dfrac{e^{-x}}{x^2+\epsilon^2}dx$.ここで,$x=\epsilon\ \text{tan}t$とおく.
$f(i\epsilon )-f(-i\epsilon)=\dfrac{2}{i\pi}\displaystyle\int_{0}^{\dfrac{\pi}{2}} e^{-\epsilon\ \text{tan}t}dt$.$\epsilon>0$だから$t\in [0,\frac{\pi}{2})$に対し$|e^{-\epsilon\ \text{tan}t}|\leq 1$.よってLebesgueの収束定理により
$(\text{与式})=\dfrac{2}{i\pi}\displaystyle\int_0^{\frac{\pi}{2}}1dt=-i$.$\Box$