解での微分係数の逆数を含む級数が、解の逆数和になる
今回の定理
留数定理とかで遊んでたら次を発見した。
逆数和が収束して、重複のない数列$\{a_n\}_{n\in A}$で
$\dis f(x)=\prod_{n\in A}\left(1-\frac x{a_n}\right)$とすると、
$\dis\sum_{n\in A}\frac1{a_nf’(a_n)}=-1$
$\dis\sum_{n\in A}\frac1{a_n^2f’(a_n)}=\sum_{n\in A}\frac1{a_n}$
全然不十分
$\frac1{f(-x)}$にラマヌジャンマスター定理を適用すると
$\dis\qquad\lim_{s\to n}\frac{-\sin(\pi s)}{\pi}\int_{0}^{\infty}\frac{x^{-s-1}}{f(-x)}dx=\frac{1}{n!}\frac{d^n}{dx^n}\Bigg|_{x=0}\frac1{f(x)}$
で、左辺の積分をハンケル路(の逆向き)と大きい円に変形する。その経路を$C$とする。
ハンケル路の方は積分の前に$\frac1{1-e^{-2i\pi s}}$が付いて、大きい円での積分は0にいく。(省略)
つまり
$\dis\qquad\begin{align}\frac{-\sin(\pi s)}{\pi}\int_{0}^{\infty}\frac{x^{-s-1}}{f(-x)}dx&=\frac{-\sin(\pi s)}{(1-e^{-2i\pi s})\pi}\int_{C}\frac{x^{-s-1}}{f(-x)}dx \\ &=-\frac{e^{i\pi s}}{2i\pi}\int_{C}\frac{x^{-s-1}}{f(-x)}dx \end{align}$
で、留数を計算する。
$x=-a_n$で一位の極を持つ。
$\dis\qquad -\frac{e^{i\pi s}}{2i\pi}\int_{C}\frac{x^{-s-1}}{f(-x)}dx=-e^{i\pi s}\sum_{m\in A}\frac{(-a(m))^{-s-1}}{-f’(a(m))}$
よって
$\dis\qquad\sum_{m\in A}\frac{a(m)^{-n-1}}{f’(a(m))}=-\frac1{n!}\frac{d^n}{dx^n}\Bigg|_{x=0}\frac1{f(x)}$
完成！$n=0,1$のときを上に載せた。
まずマスター定理を使うために$f(x)$に制限がかかるし、ハンケル路あるから多価関数になったらまずそう。あと、$a_n$に負の実数が含まれてたらこの経路じゃ囲えないので駄目そう。
$\to$コメント欄、別証明で解決してくださいました！ vunu さんありがとうございます。
これだけでも、へ〜って感じだが、色々してたら結構面白かったので書いていく。
複雑な級数の生成
まずは普通に$a_n$を定めてみる
$a_n=n^4$
$\qquad a_n=n^4\qquad(n\in\mathbb{N})$
とすると
$\qquad \dis f(x)=\frac{\sin(\pi\sqrt[4]x)\sinh(\pi\sqrt[4]x)}{\pi^2\sqrt x}$
となる。(証明略)
微分の計算
で、$f’(x)$を計算しなければならない
ややこしそうだけど、欲しいのは$f’(a_n)=f’(n^4)$だけなのでちょっと工夫できる。
$f(x)$が$x=n^4$で解を持つ原因となっている$\sin(\pi\sqrt[4]{x})$と、(その他)に分けて積の微分を実行すれば、(その他)が微分される項は$x=n^4$で消えるので、
$\qquad \dis \begin{align}f’(n^4)&=\frac{\left(\dis\frac d{dx}\sin(\pi\sqrt[4]x)\right)\sinh(\pi\sqrt[4]x)}{\pi^2\sqrt x}\Bigg|_{x=n^4} \\ &=\frac{\cos(\pi\sqrt[4]x)\sinh(\pi\sqrt[4]x)}{4\pi x^{\frac54}}\Bigg|_{x=n^4} \\ &=\frac{\cos(\pi n)\sinh(\pi n)}{4\pi n^5} \end{align} $
と、いうことで
$\begin{align} \qquad&\dis\sum_{n\in\mathbb{N}}\frac1{a_nf’(a_n)} \\ =&\sum_{n\in\mathbb{N}}\frac{1}{n^4\frac{\cos(\pi n)\sinh(\pi n)}{4\pi n^5}} \\ =&4\pi\sum_{n\in\mathbb{N}}\frac{(-1)^nn}{\sinh(\pi n)} \end{align}$
なんとこれが定理より、-1になるので
$\dis\sum_{n\in\mathbb{N}}\frac{(-1)^{n+1}n}{\sinh(\pi n)} =\frac1{4\pi}$
また、定理の二段目を使うと
$\qquad\dis\sum_{n\in\mathbb{N}}\frac1{n^4}=\frac{\pi^4}{90}$
なので、
$\dis\sum_{n\in\mathbb{N}}\frac{(-1)^{n+1}}{n^3\sinh(\pi n)} =\frac{\pi^3}{360}$
を得る。
この式自体はまぁまぁ有名なので目新しさはないけど、結構あっという間に証明できてしまった。
$a_n=q^{-n}\qquad(0\le n \le N-1)$
この時
$\dis\qquad f(x)=(x;q)_N$
となる。(qポッホハマー)
$f’(q^{-n})$を計算する。
$\dis\qquad\begin{align}
f’(q^{-n})&=(1-xq^{-n})’\prod_{0\le k \le N-1,k\neq n }(1-q^{-n+k})\\
&=-q^{-n}\prod_{0\le k\le n-1}(1-q^{-n+k})\prod_{n+1\le k\le N-1}(1-q^{-n+k})\\
&=-q^{-n}\prod_{1-n\le k\le 0}(1-q^{k-1})\prod_{0\le k \le N-n-2}(1-qq^{k})\\
&=-q^{-n}(-1)^n\prod_{0\le k\le n-1}q^{-k-1}(1-qq^{k})(q;q)_{N-n-1}\\
&=-(-1)^nq^{-n}q^{-\frac{n(n+1)}2}(q;q)_{n}(q;q)_{N-n-1}
\end{align}$
見栄えのために、$N\to N+1$として、
$\dis\sum_{0\le n \le N}\frac{(-1)^nq^{\frac{n(n+1)}2}}{(q;q)_n(q;q)_{N-n}}=1$
$\dis\sum_{0\le n \le N}\frac{(-1)^nq^{\frac{n(n-1)}2}}{(q;q)_n(q;q)_{N-n}}=\frac{1-q^{N+1}}{1-q}$
この式もそれ自体はq二項定理とかで示せるので別にって感じだけど、$a(n)$を$q^{3n-1},q^{3n-2}$とか複雑にしたらすぐに変な式得られて楽しい。
好きな解と微分係数を持つ関数
最初の証明で、
$\dis\qquad f(x)=\left(1+\sum_{n\in A,m\in\mathbb{N}}\frac1{a_n^{1+m}f’(a_n)}x^m\right)^{-1} $
が分かる。
この式、$f(x)$の解とその微分係数で$f(x)$を表しているが、逆に解とその微分係数を決めると上の式でその関数を作ってくれる。
試しに解が$x=n\quad(n\in\mathbb{N})$、そこでの微分係数が$\sqrt n\sin n$になるようにしてみる。(本当に適当)
こうなった。
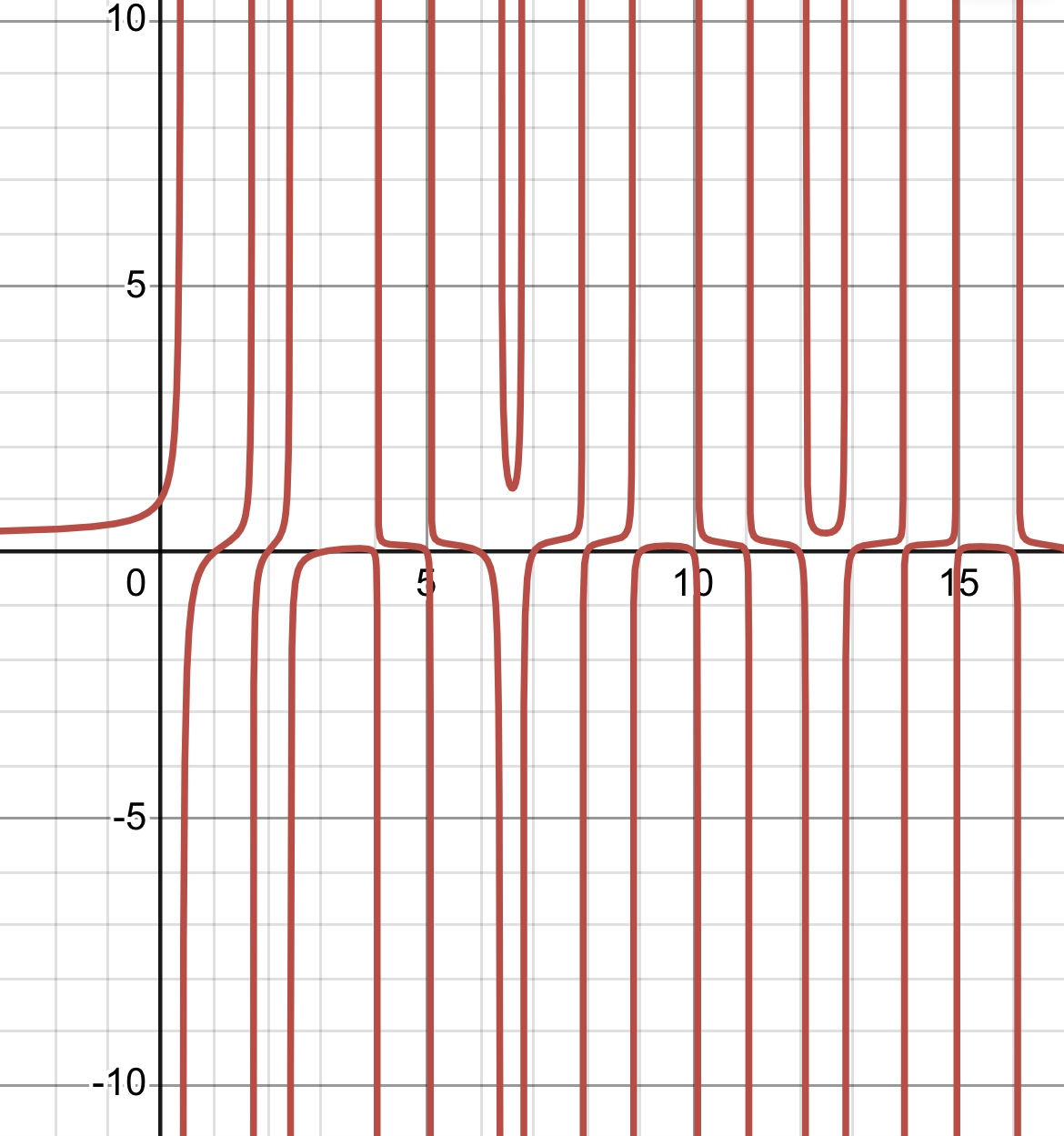もちろん成り立ってる
まぁ、だからなんだって感じだけど、微分係数も定められるのは新しい、かも？
偶成分が相反公式みたいな関数
意味不明な目次
$a_n$で作った$f(x)$を用いて、解が$x=a_n-\alpha,a_n+\alpha$の関数を作る。
$\dis\qquad\prod_{n\in A}\left(1-\frac{x}{a_n+\alpha}\right)\left(1-\frac{x}{a_n-\alpha}\right)=\frac{f(x+\alpha)f(x-\alpha)}{f(\alpha)f(-\alpha)}$
となるので、
$\dis\begin{align} \qquad&\sum_{n\in A}\frac1{(a_n+\alpha)\left(\frac{f(a_n+2\alpha)f’(a_n)}{f(\alpha)f(-\alpha)}\right)}+\sum_{n\in A}\frac1{(a_n-\alpha)\left(\frac{f’(a_n)f(a_n-2\alpha)}{f(\alpha)f(-\alpha)}\right)}=-1 \\ \\ &-\frac1{f(\alpha)f(-\alpha)}=\sum_{n\in A}\frac1{(a_n+\alpha)f’(a_n)f(a_n+2\alpha)}+\sum_{n\in A}\frac1{(a_n-\alpha)f’(a_n)f(a_n-2\alpha)} \end{align}$
ということで
$\dis g(x)=-2\sum_{n\in A}\frac1{(a_n+x)f’(a_n)f(a_n+2x)}$
という、なんかよく分からん級数の関数を定義すると、その偶成分が
$\dis\frac{g(x)+g(-x)}{2}=\frac1{f(x)f(-x)}$
と書ける。
絶妙に凄さがよく分からない。
なんか面白そうな活用方法あればください
モジュラーっぽい関数の生成
今までのは前座で、最早この話題を紹介するためだけにこの記事を書いてる。
解を$x=a_n,\alpha a_n$
とすると
$\qquad\dis\prod_{n\in A}\left(1-\frac{x}{a_n}\right)\left(1-\frac{x}{\alpha a_n}\right)=f(x)f\left(\frac x{\alpha}\right)$
となるので、
$\dis\begin{align} \qquad\sum_{n\in A}\frac1{a_nf’(a_n)f\left(\frac{a_n}{\alpha}\right)}+\sum_{n\in A}\frac1{\alpha a_nf(\alpha a_n)f’(a_n)}=-1 \end{align}$
を得る。
よって
$\qquad\dis\phi(x)=\sum_{n\in A}\frac1{a_nf’(a_n)f(xa_n)}$
とすると、
$\qquad\phi(x)+\phi(\frac1x)=-1$
が成り立つ。微分して二乗すると
$\qquad\phi’(\frac1x)^2=x^4\phi’(x)^2$
うおーー。
僕だけかも知らんけど、$x$と$-x$の関係式より、$x$と$\frac1x$の関係式ってなんか特別に感じる。まあ、偶関数に$\log x$入れたらなんぼでも作れるけど。そう言うのじゃなくて。
もうあとは周期性があれば(ほぼ)モジュラー形式、ということで
$\qquad a_n=(n-\frac12)^2\qquad(n\in\mathbb{N})$
を持ってくる。このとき
$\qquad f(x)=\cos(\pi \sqrt x)$
なので
$\qquad\dis\phi(x)=\frac2{\pi}\sum_{n\in\mathbb{{Z}}}\frac{(-1)^n}{(n-\frac12)\cos\left(\pi \sqrt x (n-\frac12)\right)}$
とすると
$\dis\qquad\phi’\left(\frac1x\right)^2=x^4\phi’(x)^2$
となる！
周期のために$F(x)=((\phi(x^2))’)^2$とすれば偶関数にもなって、
$\dis\qquad F(x+2)=F(x)$
$\dis\qquad F\left(-\frac1x\right)=x^4F(x)$
となる。ほぼモジュラー！
嬉しいけど、僕はどうしても普通のモジュラー形式をこの方法で作ることはできなかった。
できたら特殊値とかもっと色々できたかも。
因みにこの関数はモジュラー群の部分群
$\qquad\dis\left\langle\begin{pmatrix}1&2\\0&1\end{pmatrix},\begin{pmatrix}0&-1\\1&0\end{pmatrix}\right\rangle$
で対称性がある。
で、これは
成分を2で割ったあまりが、
$\begin{pmatrix}1&0\\0&1\end{pmatrix} \quad\begin{pmatrix}0&1\\1&0\end{pmatrix}$
のどっちかになる、行列式が1の集合ということになる。(にわかなので多分)
次元とかリーマン面とか考えたらなんか面白いことが分かりそう？
さらに$x=a_n,\alpha a_n,\beta a_n$とすれば何変数関数でも似たような関係式を得られる。
おわり
$\sinh$の級数とか難しいと思っていたけど、なんとすぐ示せた。
$q$級数もできて、$x,\frac1x$の関係式も得られて、とても楽しい。
さらに$f$を何乗かしても似たようなことができる。
$f$が有限の多項式でも成り立つので、受験の武器にもなるかも？(そんな場面ないか)
間違いあれば指摘ください
見てくれてありがとうございました
この記事を高評価した人
この記事に送られたバッジ
投稿者
