中高生のための集合論入門
はじめに
こんにちは、みねみねです。
普段は数学部にて整数問題をはじめとする数学オリンピック対策問題を出題しているのですが、数学部の活動の一環として数学教育も行いたいと思い、この記事を執筆しました。
中学校、また高校での数学と大学数学の雰囲気の違いを味わっていただけたら幸いです。
ところで、高校までの数学と大学数学の決定的な違いは何でしょうか。
...
それは、「厳密さ」です。
問題に回答する際の論理の厳密さとか、そういうレベルではありません。「数学という体型そのものの厳密さ」です。
あなたは「自然数とはなんですか?」と訊かれたときにうまい受け答えが思い浮かぶでしょうか。「正の整数」と答えても「じゃあ、整数ってなんなの?」と言われてしまいそうです。そうしてくるうちに、私達は「そもそも自然数ってなんなんだろう」という迷走に陥ります。
自分自身がよくわかっていない概念を用いて数学をするということはリスキーです。...というよりかは、ちゃんと定義されていないものを用いて数学をすることは論理的とは言い難いうえ、体系そのものの崩壊を招きます。
...
そのことを理解するために、本題に入る前ですが命題論理について軽く触れておきましょう。
「ならば($ \Longrightarrow $)」という記号(数理論理学においては、命題や文を構成する要素はすべて「記号」とするシステマチックな考え方をする)は、2つの命題$p,q$が存在するとき、「$p \Longrightarrow q$」という一つの命題を作り出すことができます。私たちが普段使っている言語を用いると、この命題は「$p$ならば$q$である」を意味し、これは$p$そのものや$q$そのものとは全く異なる命題となります。
具体例を見てみましょう。$p$を「1=2である」、$q$を「5=5である」と定義します。このとき、「$p \Longrightarrow q$」が意味するものは「$1=2$ならば$5=5$である」です。もちろん、$p$は偽で$q$は真です。では、「$p \Longrightarrow q$」の真偽はどうなるのでしょうか。
正解は、「真」です。実際に証明してみましょう。
$1=2$であるから、$1 \cdot 0=2 \cdot 0$すなわち$0=0$
$0=0$であるから。$0+5=0+5$すなわち$5=5$
$1=2$から正しい(と認められている)推論を用いて$5=5$が導けたため、$p\Longrightarrow q$は真である。
ここで、私たちは大胆な一般化を行います。それは、「具体的な命題の内容にかかわらず、その真偽のみで$p\Longrightarrow q$の真偽を定める」ということです。
実際にやってみます。
真偽の表
| $p$ | $q$ | $p\Longrightarrow q$ |
|---|---|---|
| 真 | 真 | 真 |
| 真 | 偽 | 偽 |
| 偽 | 真 | 真 |
| 偽 | 偽 | 真 |
1.真⇒真
言うまでもなく真
2.真⇒偽
これ(この推論)が真だったら、もうなんでもアリじゃんか
3.偽⇒真, 4.偽⇒偽
推論のスタートが偽なんだからどんな結論が出たっていいよね?
このことから、とある命題$p$が存在し、$p$が偽のとき、命題$q$と$ \lnot q$(数理論理学では$q$の否定を$\lnot q$と書く)について、$p \Longrightarrow q$と$p \Longrightarrow \lnot q$の両方が真になります!つまり数学をする際に、もともと矛盾を孕んだ定義から何かを推論するとあらゆる命題に対してそれとその否定が示せてしまいます。推論によりあらゆる箇所で矛盾するわけです。
ですから!!!!!
数百年前の偉大な数学者は!!!!!!
「厳密な体系」の構築を進めてきたんです!!!!!!!!!!!
...
自然言語を排斥した厳密な数学、それが「現代数学」というわけです。
どうしてここまで「厳密性」が大切になっているのか、少しは分かっていただけたでしょうか?
というわけで、現代数学の最も根底にある「集合」というものを掘り下げていき、厳密さが大事になってくる大学数学の雰囲気を味わっていきましょう!!
目次
前篇 集合論の夜明け
高校で習う集合。それは本当に「集合」と呼べるのでしょうか..?
この章では高校での集合を復習していきながらパラドックスを通して"ZFが定められた理由"について考えていきます。
後篇 写像と濃度
高校までは直感的な理解も大切とされる数学ですが、ときに直感を排除した抽象的な議論が要請されることがあります。この章ではそれを体験するために「濃度」という集合の基本概念と戯れながら集合についての知見を深めていきます。
では、本編へれっつらごー!
前篇 集合論の夜明け
どーでもいい話なんですけど、高校で集合を学ぶとき、たった数時間で履修し終えてしまうのはどうなのかなって思います。集合についてもっと学ぶべきことがたくさんあるのに$A \cup B$の要素の数を求めたりして満足するのは危険なのではないでしょうか? まあ、高校までだとあまり集合を使わないからいいのか...
はい! ってな訳で集合について復習していきます! まだ習っていない中学生の方でもわかるように書くので逃げないでください!
集合とはなにか
突然ですが高校生のみなさん! 「集合ってなんですか?」と訊かれたらなんて答えますか? みなさんはきっと、「モノの集まり」と答えてくれるのではないでしょうか。
偉い!!!めちゃくちゃ偉いです!!!集合は必ずしも「数のみを集めたもの」ではないですからね!それを意識して、あえて「モノ」という言葉を選んだのでしょう!!これからもその感性を大切にしてほしいです()
図にするとこんなふうになります。
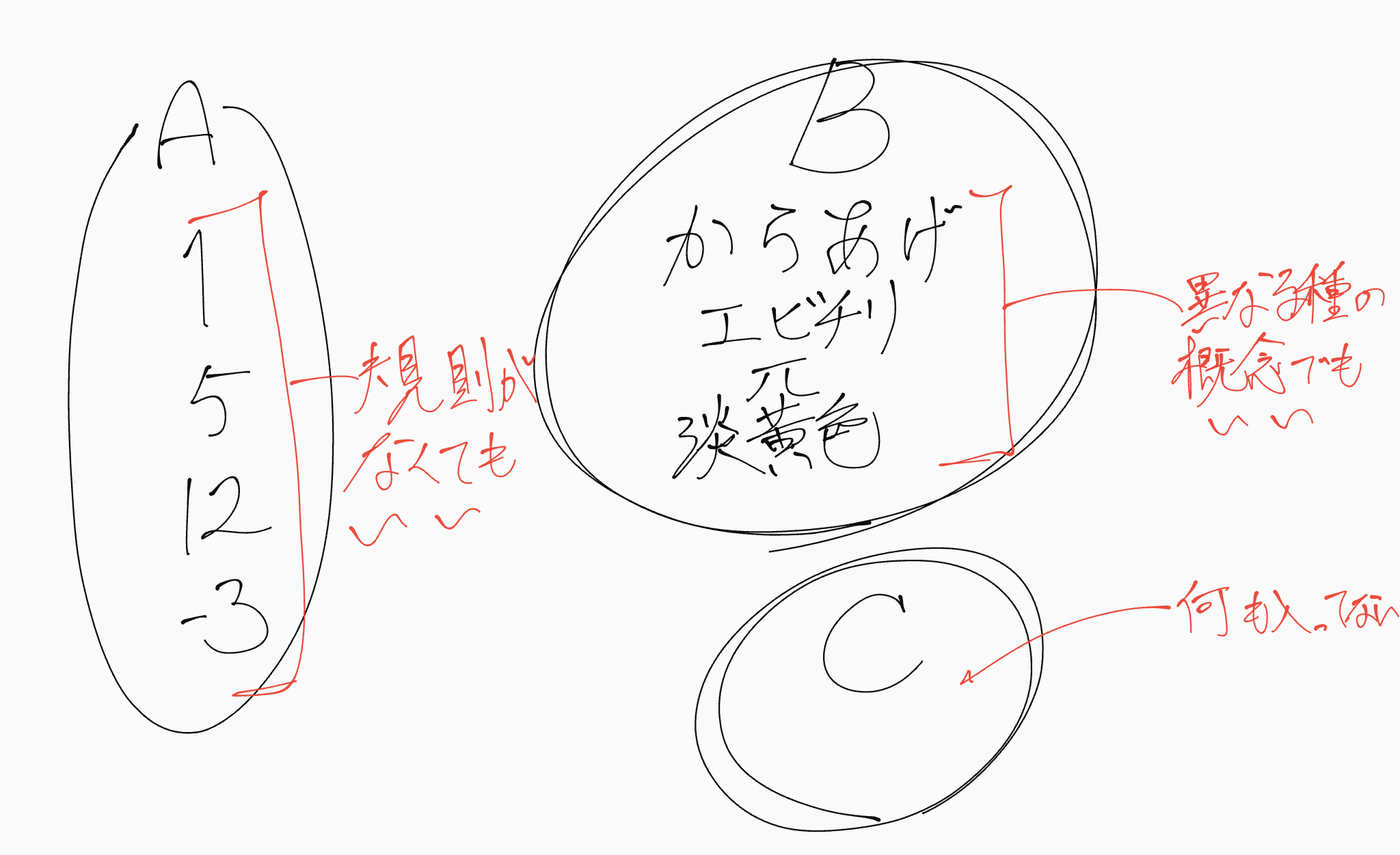 集合のイメージ
集合のイメージ
数と色とか、ジャンルが違っても一緒に集められていたらそれは「集合」なんですね〜 あと、「なにも集めていない、空っぽな集合」ってものも考えることができます。これを「空集合」といい、$\varnothing$という記号で表します。
集合の中身ひとつひとつのことを、その集合の要素といいます。たとえば、図の左上にある集合Aの要素は「1,5,12,-3」の4つです。
集合と要素の関係は次のように書きます。
$a$が集合$A$の要素であるとき、$a \in A$と表す。
$a$が集合$A$の要素でないとき、$a \notin A$と表す。
さきほどの図において、
・$1 \in A$
・$12 \in A$
・$\pi \in B$
・ハンバーグ$ \notin B$
・$x \notin \varnothing$($x$は任意の概念)
である。
ここで、集める要素が決まれば集合が定まります。つまり、要素の情報を用いて集合が記述できるのです。
集合の決定(記述)の仕方は二つあります。
一つ目は、要素を列挙するやり方。
$A= \lbrace 1,5,12,-3 \rbrace $のように、$\lbrace\,\rbrace$で要素を囲んで集合を記述できます。
二つ目は、要素の規則を書くやり方。
たとえば、$A=\lbrace x|x\text{は2の倍数}\rbrace$のように書きます。
また、同じ集合を表すものとして、$A=\lbrace 2x|x\text{は整数}\rbrace$のような書き方もできます。とにかく、$\lbrace \text{要素}|\text{要素の満たす条件}\rbrace$という書き方をします。
この二つの記法は時と場合によって使い分けます。使い分けについては、集合に慣れ親しんだら自然と身につくのでそこまで怖がらなくていいです!!!
基本的な集合は、最初から記号が与えられています。いちいち「$A$は自然数を表す集合です」というふうにことわらなくてもいいように、世界共通の記号が定められているのです。
$\mathbb{N}$...自然数全体の集合
$\mathbb{Z}$...整数全体の集合
$\mathbb{Q}$...有理数全体の集合
$\mathbb{R}$...実数全体の集合
$\mathbb{C}$...複素数全体の集合
その他にも様々な記号がありますが、今は勉強しなくても大丈夫でしょう。
これらの記号のおかげで、さきほどの「要素の規則を書く記述法」がとても楽になりました! 具体的に様々な集合を記述してみましょう!
偶数全体の集合 $\lbrace 2x | x \in \mathbb{Z} \rbrace$
奇数全体の集合 $\lbrace 2x+1|x\in\mathbb{Z}\rbrace$
ここで、この記述法の理解度を試すために次の問題を解いてみましょう。
次の集合はどのような集合だろうか。
1.$\lbrace k^2|k\in \mathbb{Z}\rbrace$
2.$\lbrace \frac{b}{a}|a\in\mathbb{Z},b\in\mathbb{Z},a\neq0\rbrace$
解答
1.平方数全体の集合
2.$\mathbb{Q}$(有理数全体の集合)
集合は、要素の種類のみに着目するため「要素の重複」や「並び方」にこだわりはない。あくまでもサラダボウルのようなイメージ
$\lbrace 1,1,2,3\rbrace=\lbrace 1,2,3\rbrace$ (重複は無視)
$\lbrace 8,1,5\rbrace=\lbrace 1,5,8\rbrace$ (順番は無視)
部分と濃度
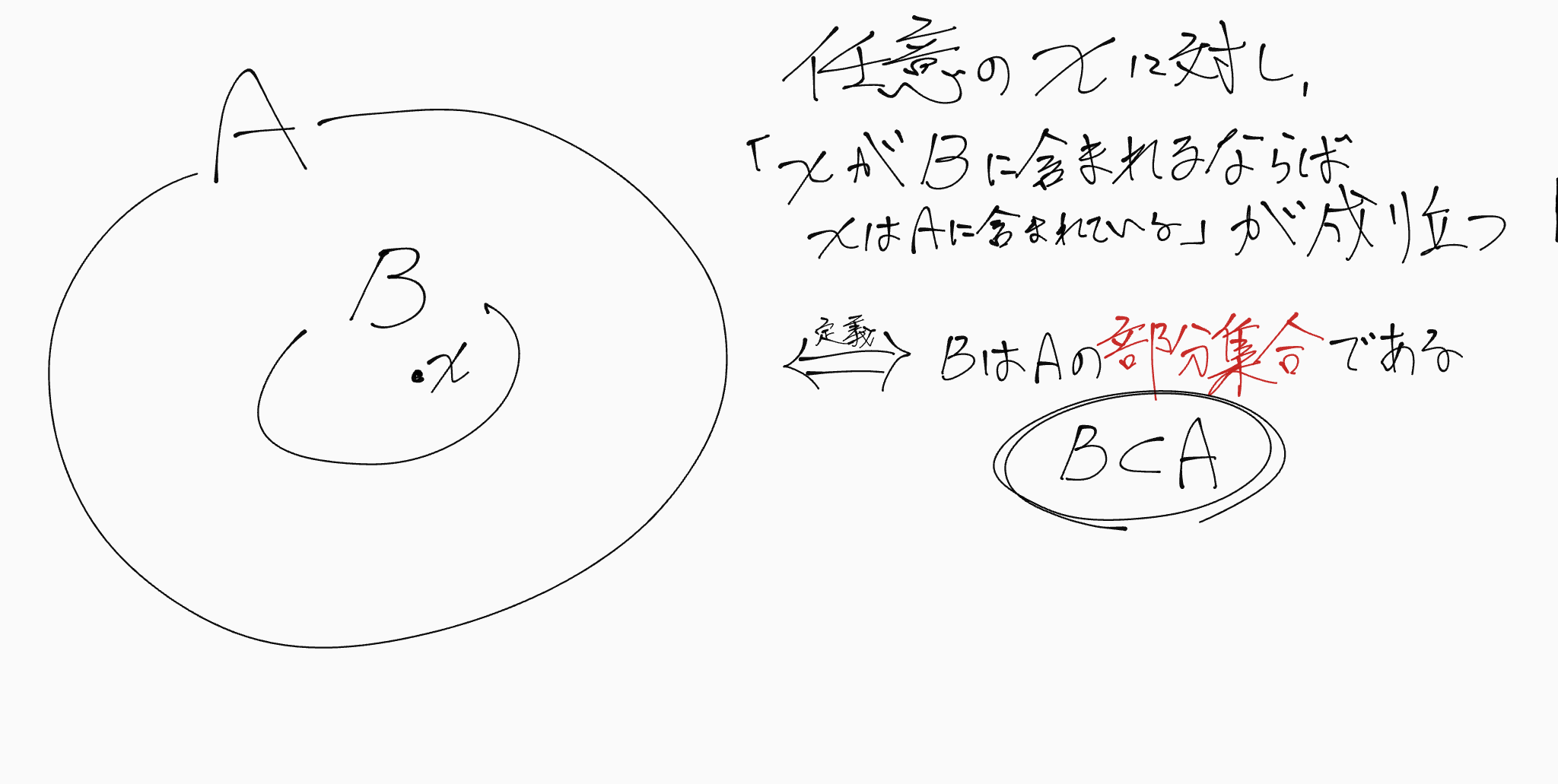 部分集合の定義
部分集合の定義
「$B$が$A$の部分集合である」とは、どんな$x$に対しても$x\in B \Longrightarrow x\in A$が成り立つということである
そして、このことを$B \subset A$と書く
部分集合という新しい概念が出てきました! 簡単に言うと、「まるまる含まれた集合」ってことですね! この概念は、「ありがたい概念」というよりかは「自然と考えられる概念」です。
では、具体例をいくつかみていきましょう。
$\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}\subset\mathbb{C}$
$\lbrace\text{赤,青}\rbrace\subset\lbrace x|x\text{は虹色を構成する色}\rbrace$
任意の集合$A$について、
$\varnothing\subset A$,$A\subset A$ ($\varnothing$は空集合を表す記号)
$\text{赤}\in \lbrace x|x\text{は虹色を構成する色}\rbrace$だが、
$\lbrace\text{赤}\rbrace\subset\lbrace x|x\text{は虹色を構成する色}\rbrace$である。
これは、$\text{赤}$はただの「対象(要素)」を意味しているが、$\lbrace\text{赤}\rbrace$は「集合」を意味しているため起こることである。
もっと言うと、$\in$は「左に対象として見るものが、右に集合が来る」記号、$\subset$は「右も左も集合が来る」記号である。
今後学習する際は「ただの対象なのか、集合なのか、」を意識して臨むべきである。
同様の理由で、$\mathbb{N}\notin\mathbb{Z}$だが、$\mathbb{N}\subset\mathbb{Z}$である。$\mathbb{Z}$というものは「数」を要素として持つものであり、$\mathbb{N}$という「集合そのもの」を要素には持たない。
 伝われ〜!!!!!!
伝われ〜!!!!!!
ついでに冪集合(べき集合)という概念についても触れておきます。
これを見ると、集合はホントーに「何でもアリ」なんだなっていう気持ちになります!!!!
ある集合$A$の部分集合ひとつひとつを要素としてもつ集合を$A$の冪集合といい、$\mathscr{P}(A)$と書く。
う〜ん...よくわかりませんね...
つまりは、「集合は、数字でも惣菜でも、どんなものも要素にしていい。なんなら、集合を要素として持つような集合を考えてもいい」ってことです。
言葉で説明してもわかりにくいので例をみてみましょう。
$A=\lbrace0,1\rbrace$とする。
$A$の部分集合は、$\varnothing,\lbrace0\rbrace,\lbrace1\rbrace,\lbrace0,1\rbrace$の四つがある。
よって、$\mathscr{P}(A)=\lbrace\varnothing,\lbrace0\rbrace,\lbrace1\rbrace,\lbrace0,1\rbrace\rbrace$である。
ここで、$\lbrace1\rbrace\in\mathscr{P}(A)$だが、$1\notin\mathscr{P}(A)$である。
もっというと、$B\subset A$というのは、$B\in\mathscr{P}(A)$というふうに書けるってことですね〜...
![!FORMULA[100][36091879][0]と!FORMULA[101][-1086707062][0]のイメージ](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Fc01UPUX8QVFiAwuAfgXw.png?alt=media) $\in$と$\subset$のイメージ
$\in$と$\subset$のイメージ
$\subset$は、あくまでも同じ次元での主従関係だけど、$\in$は、ひとつ下の次元を取り込んでいる主従関係...みたいな...
$\subset$の左右は同じレベルだけど、$\in$の左右にはレベルの差がある...みたいな...
そういう気持ちが伝わったら嬉しいです...
またまた別の概念について考えます。それは「濃度」ってヤツです。
簡単に言うと要素の個数のことです。
$\lbrace 0,1,2\rbrace$の濃度は$3$ですし、$\lbrace 1,4,9,16,25\rbrace$の濃度は$5$です。
一応記号を整理すると、$ \left| A \right| $で集合$A$の濃度を表します。たとえば$\left| \lbrace0,1,2\rbrace\right|=3$ってことです。なお、ここでは$\left| \mathbb{N} \right|=\infty$のように書くこととします(無限ってなんか扱いがいろいろめんどいんすよね...それもあとでなんとなく分かります)
濃度は(いまのところ)かんたんな概念なので次の問題を解いてみましょうか!
$\left|A\right|=n$とする。
このとき、$\left|\mathscr{P}(A)\right|=2^n$となることを示せ
解答
$\mathscr{P}(A)$の要素は$A$の部分集合であるため$A$の部分集合の個数を数えればよい。
$A$の要素$a_1,a_2,\cdots a_n$のそれぞれに対して、部分集合に含む/含まないの$2$通りが考えられるため、部分集合として考えられるものは$2^n$通り存在する。
これが、$\mathscr{P}(A)$が「冪集合」と言われる所以ですね〜 なんの感動もないですが...
はい、ってなわけで、第一章最大の山場に入ります!!!
「集合とはなにか」を疑う
第一章のはじめに、集合とは「モノの集まり」であると堂々と述べました。さらに、集合の記述法として、「要素の規則を書く書き方」というものもやりました。
ここで、$\lbrace\text{要素}|\text{要素の満たすべき条件}\rbrace$という形での集合の記述のしかたを用いて、「既存の集合(偶数の集合など)を記述する」のでなく「条件によって新たな集合を作り出す」ことができそうだという発送に至ります。てきとーに条件を定めてやれば一意に集合が決まるため、自由自在に集合がつくれる! ってことです。条件が集合の構築を支配してるって感じですね!
そういえば、問題1.1の$\lbrace k^2|k\in \mathbb{Z}\rbrace$なんて、$\lbrace\text{要素}|\text{要素の満たすべき条件}\rbrace$の形に書き換えてあげると$\lbrace x|x=k^2,k\in \mathbb{Z}\rbrace$となって条件で集合を定めているわかりやすい例と言えるでしょう。
ってなわけで、こんなハチャメチャ集合も考えることができるわけです。
$R=\lbrace x|x\notin x\rbrace$ という集合を考えてみる
ひとことで言うならば「『自分自身を要素に持たないもの』を全部集めた集合」ってことですね()
この集合を理解するために、少し復習しましょう。
$\in$と$\subset$の違い:$\in$は集合と要素という「異なる立場の主従関係」であり、$\subset$は集合どうしの主従関係である。例3のあとの注意でも「$\mathbb{N}\notin\mathbb{Z}$だが、$\mathbb{N}\subset\mathbb{Z}$である」と書いた。
集合の要素は割と自由であるため、「集合を集めた集合」を考えることもできた。具体的には冪集合がそれの一例である。
では、$R$を読み解いていきましょう!
そもそも$R$の要素$x$は「$x\notin x$」を満たしているものである。
- $1\notin 1$より、$1\in R$
- $2\notin 2$より、$2\in R$
- $\mathbb{N}\notin\mathbb{N}$より、$\mathbb{N}\in R$
- $\lbrace x|x=k^2,k\in \mathbb{Z}\rbrace\notin\lbrace x|x=k^2,k\in \mathbb{Z}\rbrace$より、$\lbrace x|x=k^2,k\in \mathbb{Z}\rbrace\in R$
なんか当たり前ですね()
逆に$x\in x$を満たすような$x$を探すのが難しいくらいです。
このまま行くと、すべての概念は$R$の要素になるのではないかという気がしてきます。...っと、おや? 様子がおかしくなってきましたよ?
前提知識
ある集合$A$が存在するとき、任意の概念$x$に対し、
- $x\in A$
- $x\notin A$
のどちらかは真でもう一方は偽である。
まあ、当たり前ですよね。ってことは、$R$に対しても同じことが言える...!
任意の概念$x$に対し、
- $x\in R$
- $x\notin R$
のどちらかは真でもう一方は偽である。
なんなら、この概念$x$を$R$にすることもできる...!!!
- $R\in R$
- $R\notin R$
のどちらかは真でもう一方は偽である。
あぁ...なんか見えてきましたね...!!
これはなんかヤバいことが起きそうです!!!!!!
1.$R\in R$のとき
$R$(左)は、$R$(右)の要素だから$x\notin x$を満たす概念である。
つまり、$R\notin R$が成り立ち、仮定の$R\in R$と導いた結論の$R\notin R$がどちらも真になることはない。よって、$R\in R$は偽。
2.$R\notin R$のとき
$R$(左)は、$R$(右)の要素でないから$x\notin x$を満たさない概念、つまり$x\in x$を満たす概念である。
つまり、$R\in R$が成り立ち、仮定の$R\notin R$と導いた結論の$R\in R$がどちらも真になることはない。よって、$R\notin R$は偽。
今、1.と2.の両方が偽であると導いたが、それは$R\in R$と$R\notin R$のどちらかは真であることに矛盾する。
な...なんで矛盾が起こってしまった!!!!
妥当な推論から生まれてしまった矛盾...これははじめにで最も恐れたこと...数学という体系そのものの崩壊です!!!!
...ってなわけで、こうならないために結局何をすればいいかというと、$\lbrace\text{要素}|\text{要素の満たすべき条件}\rbrace$という形で集合を構築するとき、条件をメチャクチャに設定できないようにすればいいと言えそうです。
この制約のおかげで矛盾を回避できそうです!!!!
このように、「集合」を「モノを好き勝手集めたもの」としてはいけません!!!!!具体的に、集合を作るうえで矛盾が起きないようにする制約たちのことを「ZF公理系」といいます。「ZF公理系」に基づいた集合を考えるのが、矛盾を引き起こさないためのキーです(だからZF公理系は現代の集合論の要です)。
(※ZFについては「おまけ」参照!)
はーい、前篇終わり!!!!
ちゃんと休憩しよう!!!!!!!!
後篇 写像と濃度
いきなりですが、さっきまで扱った内容とは全く別の概念を扱います。それは「写像」です。
あまりおすすめしませんが、「写像ってなんすか?」と調べるとたくさん動画が出てくるくらいには一部界隈で有名な言葉です()
はい、ってなわけで写像を扱っていく!!!
写像とはなにか
ある集合から別の集合へのジップラインを考えます。ここでは簡単のため集合$A$から集合$B$へのジップラインを考えます。$A$から$B$へ飛び移るのです!!!このジップラインを$f$と名付けましょう。
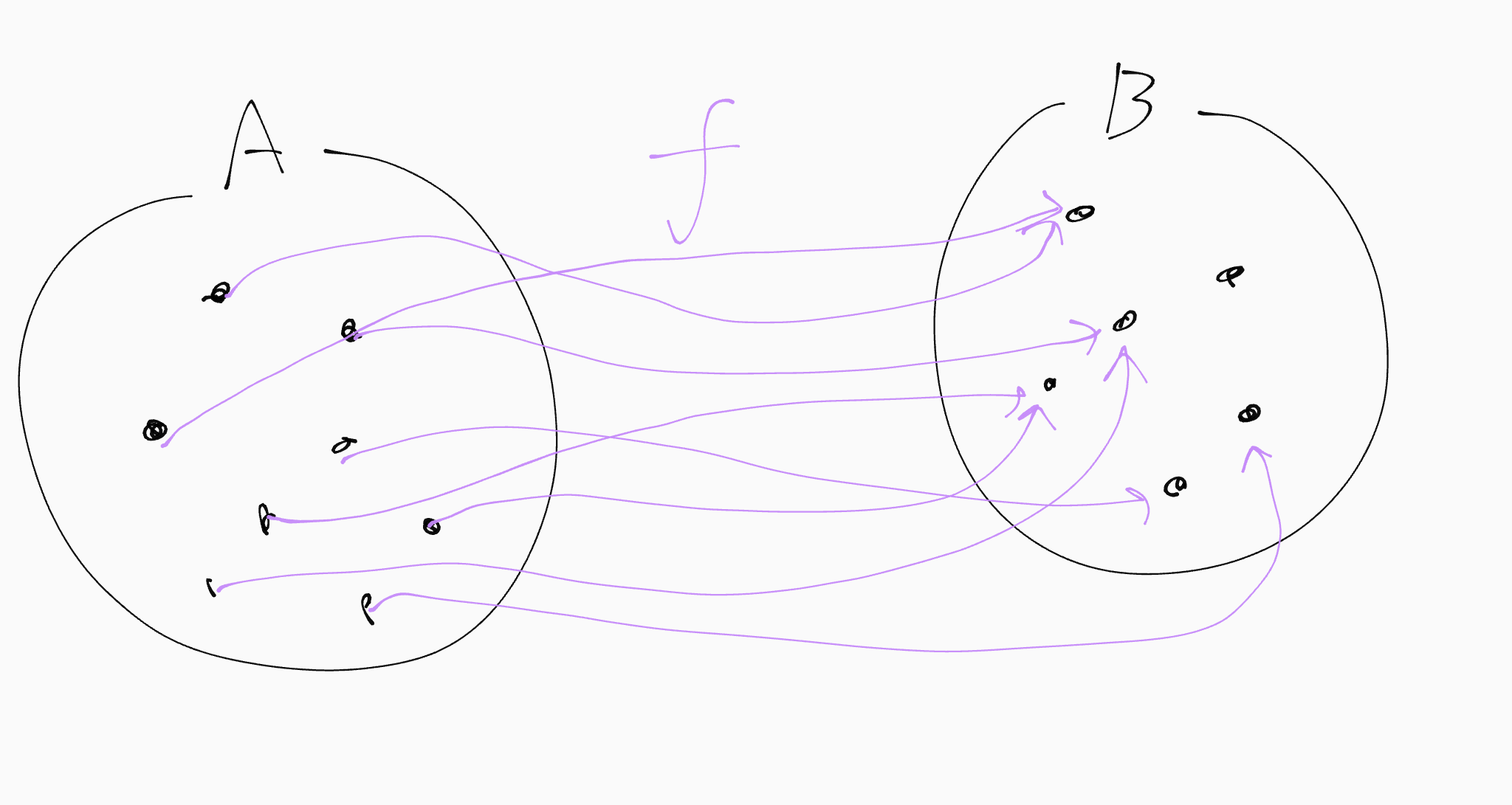 ジップライン
ジップライン
ある$A$の要素$a$があり、$f$でのそれの行き先を$f(a)$と表すことにします。
![!FORMULA[192][36229333][0]が!FORMULA[193][-114649016][0]に行く](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F8f7UdMojMhnADjfCGiyj.png?alt=media) $a_1$が$f(a_1)$に行く
$a_1$が$f(a_1)$に行く
図のように、行き先は被ってもいいです。式で表すと、$a_2\neq a_3$であっても$f(a_2)=f(a_3)$となっていいということですね。
いっぽう、一つの要素から異なる行き先に行ってはいけません。式で表すと、$a_1=a_2$のとき$f(a_1)\neq f(a_2)$となってはいけません。
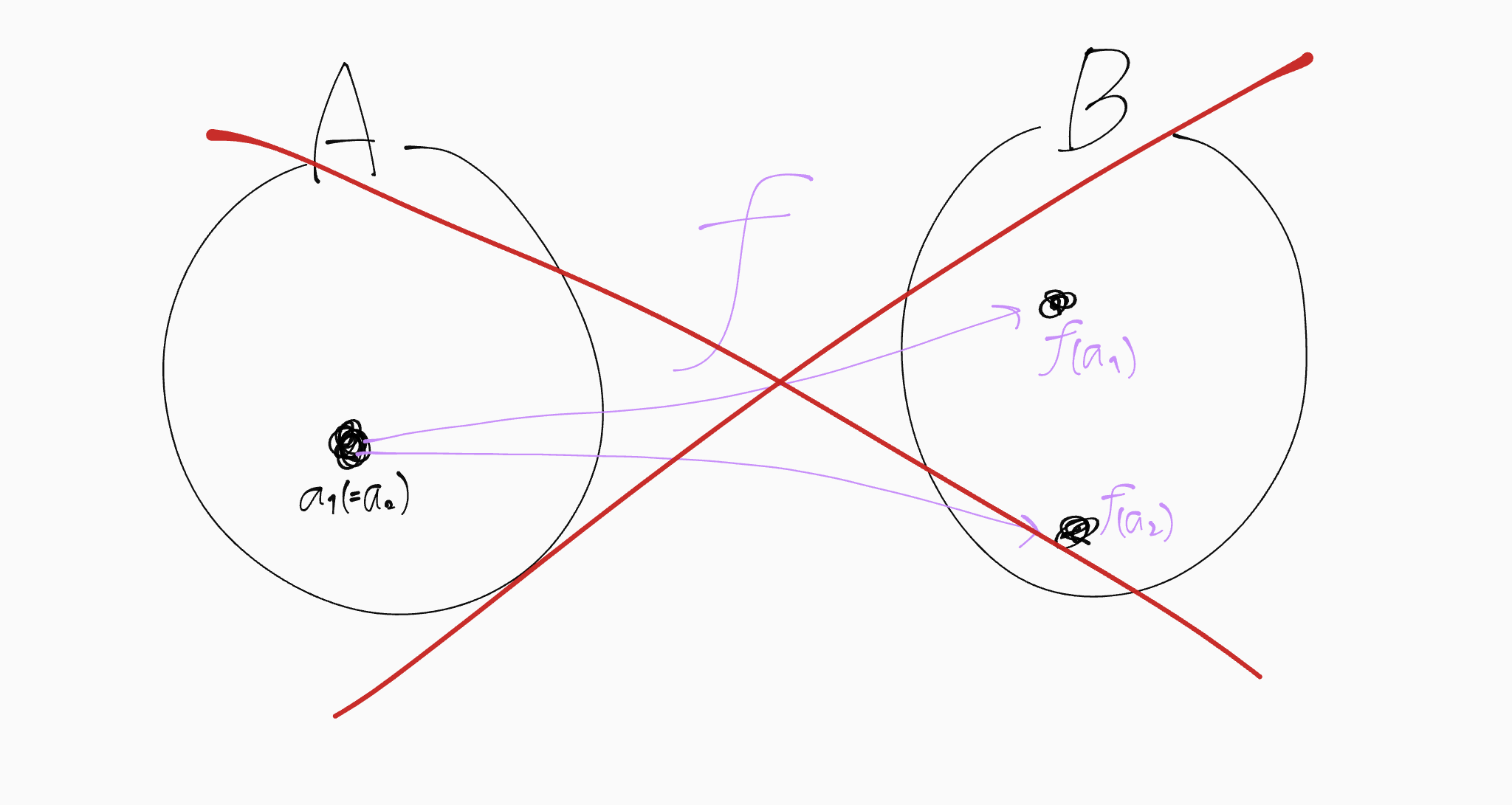 行き先が分かれてはいけない
行き先が分かれてはいけない
また、根本の集合(集合$A$)の要素に、ジップラインがつながっていないものがあってはいけません。$A$のすべての要素はジップラインで$B$にいけます。
このようなジップライン$f$のことを、「写像」と呼びます。
集合$A,B$があり、以下の規則を満たす$A$の要素から$B$の要素への対応づけを写像と呼ぶ
・$A$の各要素に対して、$B$のある要素がただ一つ対応する
写像は、以下の図のように書く
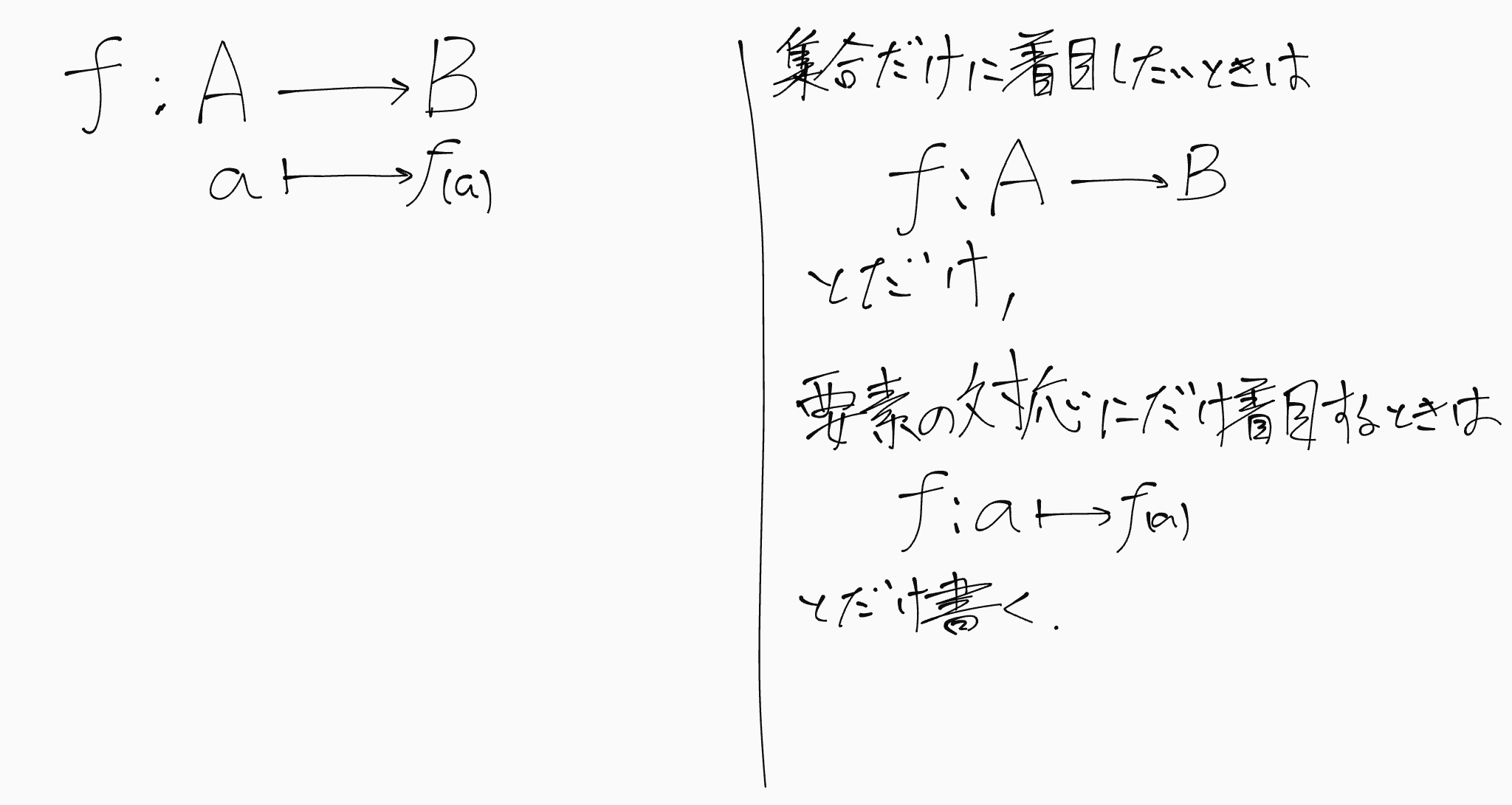 写像の書き方
写像の書き方
$f:\mathbb{R}\rightarrow\mathbb{R}$を、$f:x\mapsto x^2$と定めると、これは写像になる。
![つまり!FORMULA[209][-1103287586][0]ってこと](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FscwydnVzXS9IemhDmpcW.png?alt=media) つまり$f(x)=x^2$ってこと
つまり$f(x)=x^2$ってこと
...薄々気づいている人も多いかと思いますが、つまり写像とは関数の一般化です。なんなら、大学では数以外にも「関数」という言葉を使うので写像と関数に意味的な違いはないと認識していいです。
ところで、写像は「行き先が被っていてもいい」「行き先の集合にもれがあってもいい」のですが(さきほどの例だと$1$と$-1$は行き先が被っており、行き先の集合において$-5$とかはジップラインがつながっていない「もれ」になります)、逆に「行き先が被っていない」写像や「行き先の集合にもれがない」写像には特別な名前がついており、それぞれ、その写像が単射、全射であるといいます。
式で表すとこうなります。
写像$f:A\rightarrow B$が単射であるとは、任意の$a,a'\in A$について$f(a)=f(a')\Longrightarrow a=a'$が成り立つことを言う。
写像$f:A\rightarrow B$が全射であるとは、任意の$b\in B$について、$f(a)=b$となる$a\in A$が存在することを言う。
写像$f$が全単射であるとは、$f$が単射かつ全射であることを言う。
濃度と全単射
突然ですが、集合$A,B$の間に全単射$f:A\rightarrow B$が存在するならば$\left|A\right|=\left|B\right|$が成り立ちます。これは、$A$の要素と$B$の要素が一対一に対応しているからです。
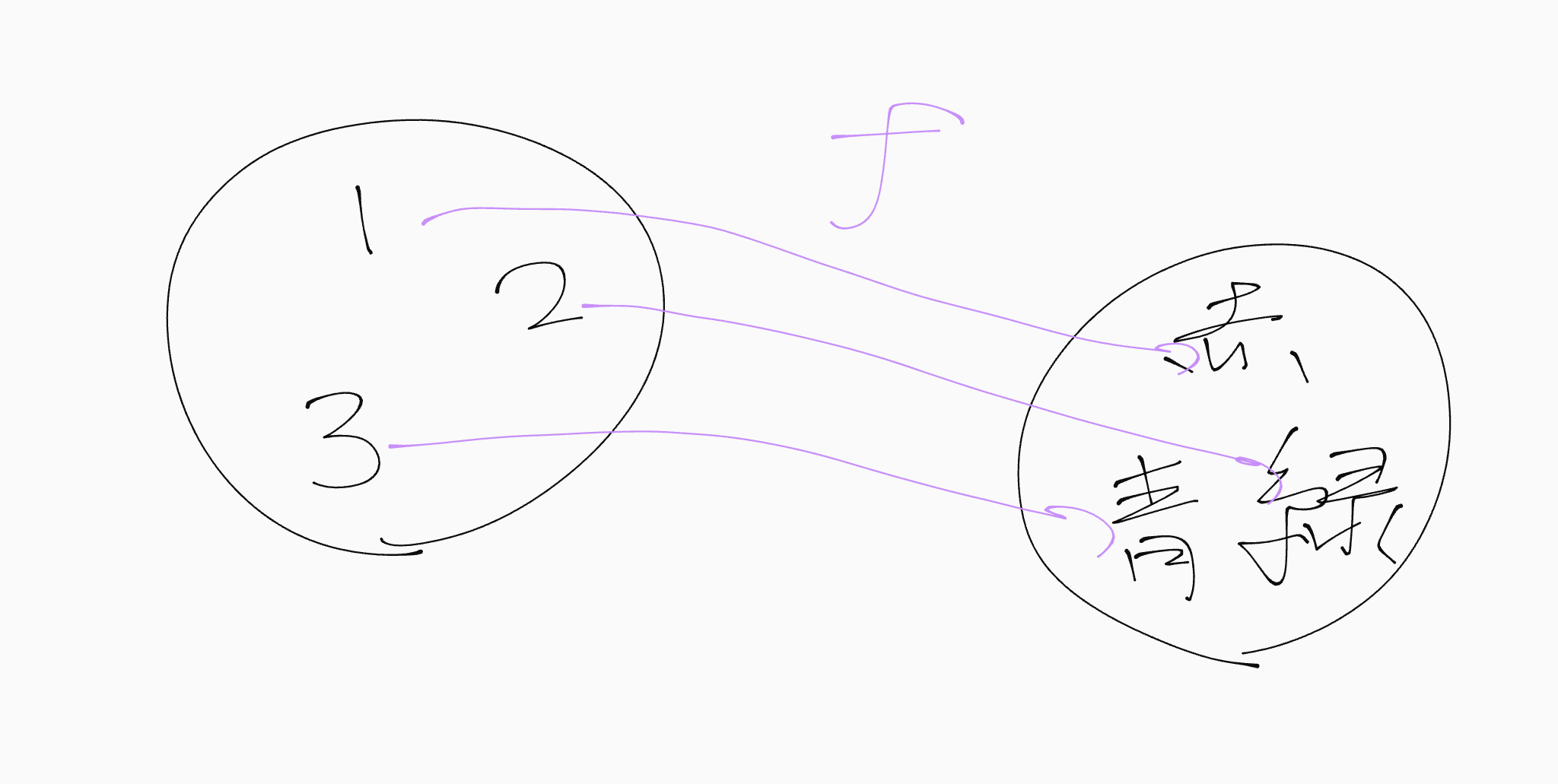 全単射が存在すると要素の数は同じ
全単射が存在すると要素の数は同じ
もちろん、全射$f:A\rightarrow B$が存在するならば$\left|A\right|\geq\left|B\right|$が成り立ちます。
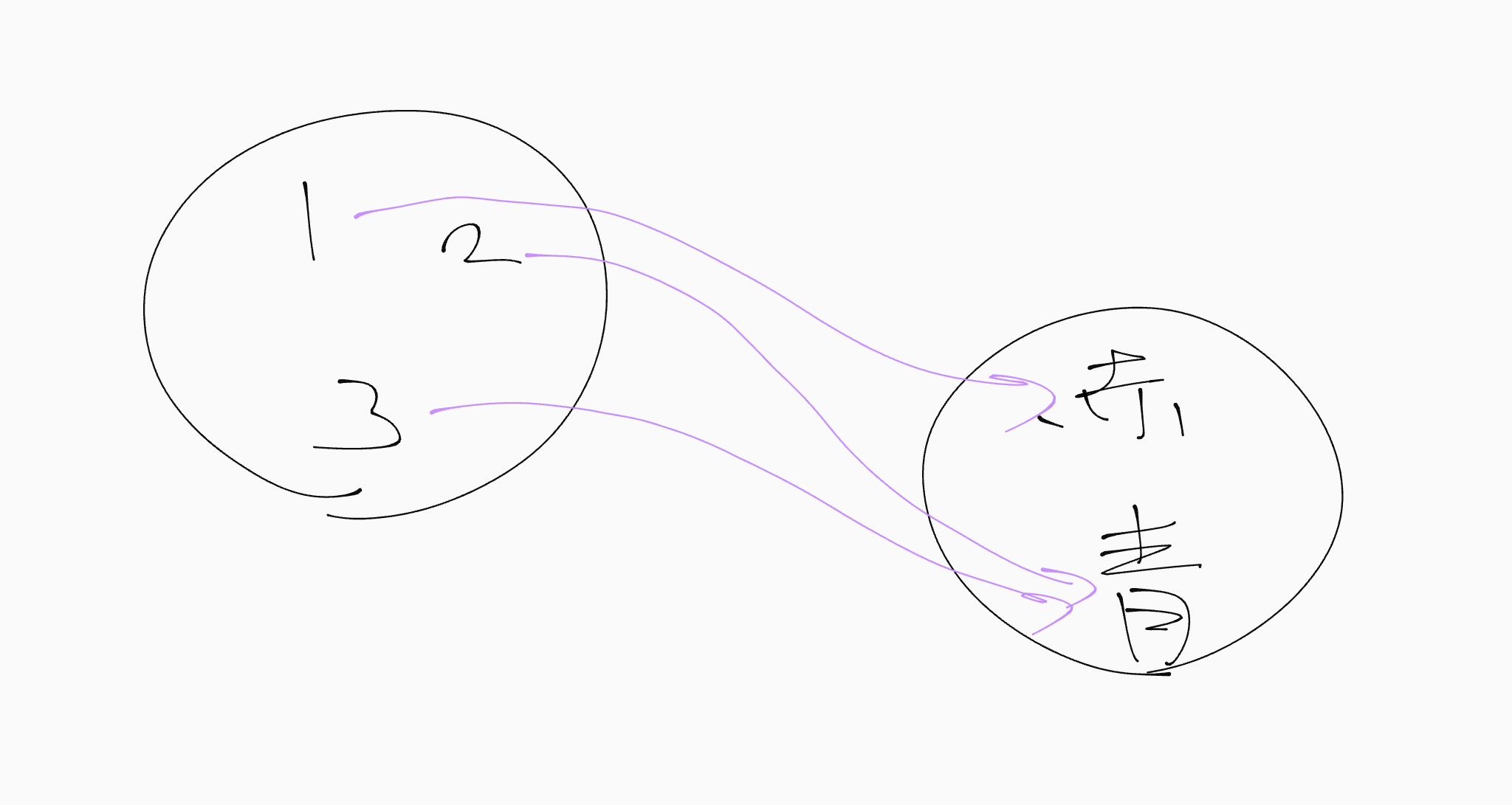 全射が存在するならば根本が多い
全射が存在するならば根本が多い
なお、$\left|A\right|\geq\left|B\right|$であって$\left|A\right|\neq\left|B\right|$のとき、$\left|A\right| \gt \left|B\right|$とします。
これらは、「無限の濃度」にも適応できます。つまり、$\left|\mathbb{N}\right|$と$\left|\mathbb{Z}\right|$の大小比較ができるようになりました。
「無限」を数える
さて、突然ですが$\left|\mathbb{N}\right|<\left|\mathbb{Z}\right|$でしょうか。それとも$\left|\mathbb{N}\right|>\left|\mathbb{Z}\right|$でしょうか(そんなわけない)。はたまた$\left|\mathbb{N}\right|=\left|\mathbb{Z}\right|$でしょうか。
直感的な話をすると、濃度とは「要素の個数」なので、$\left|\mathbb{Z}\right|$は$\left|\mathbb{N}\right|$の二倍ほどの大きさがありそうです。
では、ここで写像を用いて論理的に濃度を比較してみましょう。
写像$f:\mathbb{Z}\rightarrow\mathbb{N}$を、$x\in\mathbb{Z}$が
- 0のとき $f(x)=1$
- 正の数のとき $f(x)=2x$
- 負の数のとき $f(x)=-2x+1$
とすれば$f$は全単射になる。よって$\left|\mathbb{N}\right|=\left|\mathbb{Z}\right|$である。
なんと、直感的ではない結論として$\left|\mathbb{N}\right|=\left|\mathbb{Z}\right|$を導けました!これも、勉強していくうちにだんだん直感的にわかるようになってきます。
では、$\left|\mathbb{N}\right|$と$\left|\mathbb{Q}\right|$について考えてみましょう。$\mathbb{Q}$は稠密であり、さすがに$\left|\mathbb{N}\right|<\left|\mathbb{Q}\right|$な気がします...が、なんか様子がおかしくなってきました!!!
以下の図のように有理数を横一列に並べることができる。
なお、座標$(a,b)$を有理数$\frac{b}{a}$と同一視する。
左に出てきた数や存在しない数を消して詰め直す。
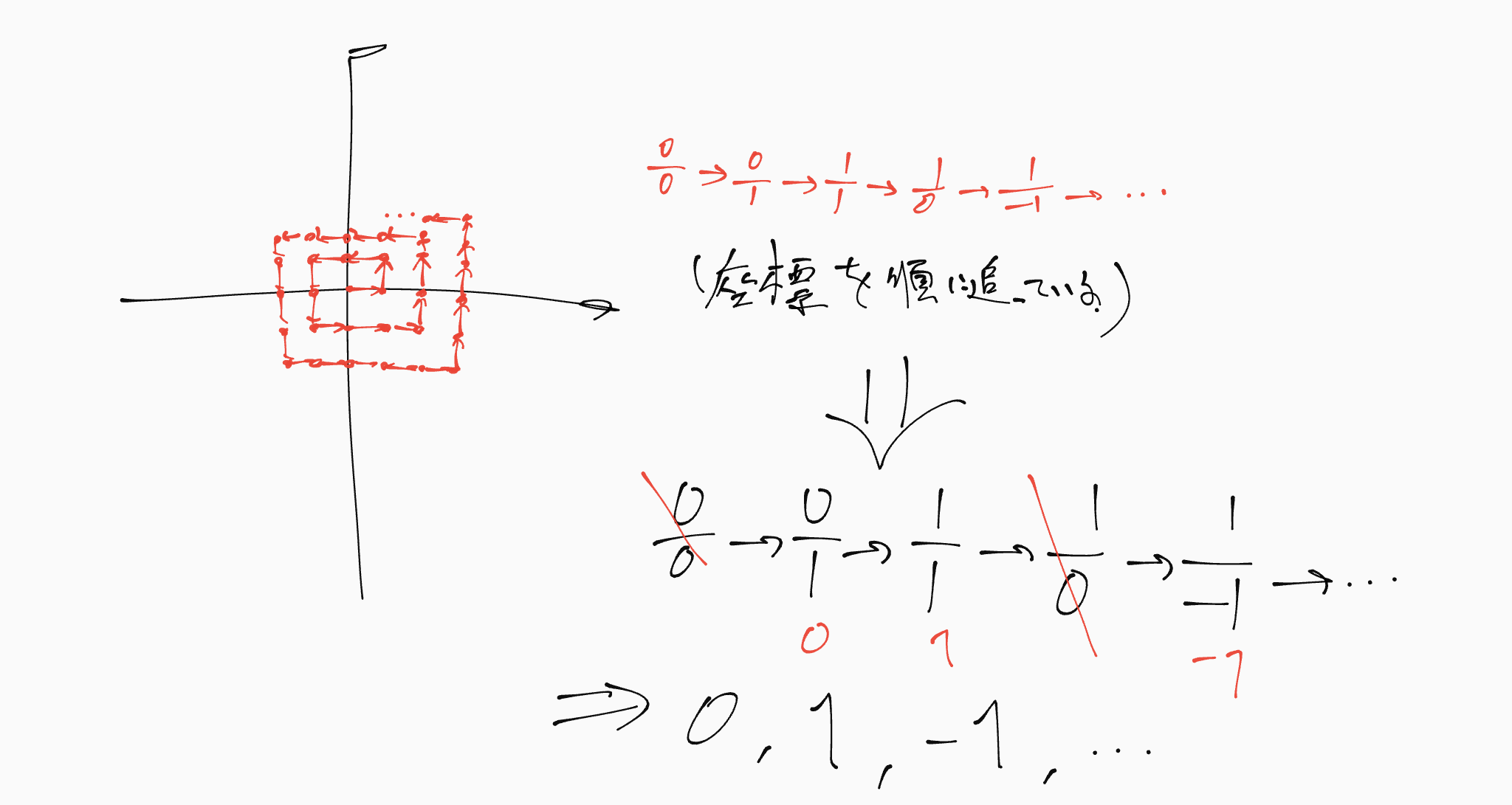 イメージ
イメージ
左から順番に自然数を対応させると、これは全単射になる。
よって$\left|\mathbb{N}\right|=\left|\mathbb{Q}\right|$。
では、$\left|\mathbb{R}\right|$はどうでしょう。結論から言うと、$\left|\mathbb{N}\right|<\left|\mathbb{R}\right|$が成り立ちます!!
全射$f:\mathbb{R}\rightarrow\mathbb{N}$が存在することは明らか。よって$\left|\mathbb{N}\right|\leq\left|\mathbb{R}\right|$。
ここで、全単射$f:\mathbb{N}\rightarrow\mathbb{R}$が存在しないことを示す。
全単射$f:\mathbb{N}\rightarrow\mathbb{R}$が存在すると仮定する。
すると$f$は全射であるから全射$f:\mathbb{N}\rightarrow[0,1]$が存在する。ただし、$[0,1]=\lbrace x\in\mathbb{R}|0\leq x\leq 1\rbrace$である。
ここで、$[0,1]$の要素は「$0.a_1a_2a_3...$」という形の無限小数で表せる。たとえば$\frac{1}{7}=0.1428571...,0.5=0.5000...,\frac{\pi}{10}=0.31415926...$である。ただし、ここでは$0.9999...=1$とする。
$f(1)=0.a_1a_2a_3...$
$f(2)=0.b_1b_2b_3...$
$f(3)=0.c_1c_2c_3...$
...
であるとき、$A=a_1\text{より1大きい数(9の次は0とする)},B=b_2\text{より1大きい数(9の次は0とする)},$同様に$C,D,...$も定義する。
ここで、$f(n)=0.ABCDE...$となる$n$について考える。
$n=1$は、小数第一位が異なるため不適。
$n=2$は、小数第二位が異なるため不適。
同様にして、このような$n$は存在しないことが言える。
よって、$f$は全射でない。
背理法により、$\left|\mathbb{N}\right|<\left|\mathbb{R}\right|$。
なんと!実数は有理数までとは違って自然数より大きいのです!
ちなみにこの証明を「カントールの対角線論法」といいます。
ところで、濃度について次のような別の定理が成り立ちます。
任意の無限集合$A$に対し、$\left|A\right|<\left|\mathscr{P}(A)\right|$である。
いちおう証明載せておきます。
全単射$f:A\rightarrow\mathscr{P}(A)$が存在すると仮定する。
ここで、$a\in A$の行き先$f(a)\in \mathscr{P}(A)$とは何かを考える。
$f(a)\in \mathscr{P}(A)$とは言い換えると$f(a)\subset A$ということであり(これは冪集合の定義である)、下のような図が描ける。
![!FORMULA[286][1126134742][0]は左右に存在する](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FIY4gAkS2pfIBNAVxJkjq.png?alt=media) $f(a)$は左右に存在する
$f(a)$は左右に存在する
ここで、左側の図に着目する。図のように、$a$が$f(a)$に含まれていないような$a$、すなわち$a\notin f(a)$を満たす$a$をすべて集めた集合を$B$とする。これは$A$の部分集合であるから、$B=\lbrace a\in A|a\notin f(a)\rbrace \subset A$つまり$B\in \mathscr{P}(A)$である。よって下のような図が描ける。
![!FORMULA[296][36678][0]も左右に存在する](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FscewECRuhpFMNSVNzrub.png?alt=media) $B$も左右に存在する
$B$も左右に存在する
ところで、$f$は全単射であったため、行き先が$B$となる$x$、つまり$f(x)=B$となる$x\in A$が存在する。
では、この$x$はどこに存在するだろうか。
もし$x\in B$ならば、
$x$は$x\notin f(x)$つまり$x\notin B$を満たす。これは過程に反する。
もし$x\notin B$ならば、
$x$は$x\in f(x)$つまり$x\in B$を満たす。これは過程に反する。
よって全単射$f$は存在しない。
いやー!!お疲れ様でした!!第二章はこれで終わりです!!「写像」が如何に重要な概念なのかが少しでも伝われば幸いです!!
ちょっとだけ補足を入れますね。
↓↓↓
$\left|\mathbb{R}\right|$も$\left|\mathscr{P}(\mathbb{N})\right|$も、どちらも$\left|\mathbb{N}\right|$より真に大きいです。実は$\left|\mathbb{R}\right|=\left|\mathscr{P}(\mathbb{N})\right|$が成り立つのですが、ここではその証明はしないこととします。
濃度について、漠然とした「不確定さ」を感じてもらうために連続体仮説の話をしようと思います。
$\left|\mathbb{N}\right|<\left|\mathbb{R}\right|$ですが、$\left|\mathbb{N}\right|< X<\left|\mathbb{R}\right|$なる濃度$X$は存在するのでしょうか。実は、このような$X$が存在することは「証明も反証もできません(?!)」。存在するとも、しないとも言い切れないのです。これは我々の研鑽が足りないのではなく、「証明も反証もできない」という命題が証明できるのです(?!?!?!)。これが意味するのは、$\mathbb{R}$の濃度は、濃度の数直線を考えたときにどこにいるのか確定していない、ということです。
この、$X$が存在するか、という問いは連続体仮説と呼ばれ、高校までの数学では味わえない「未知」を体感するのにとっておきの題材です。ちょっと長くなりましたが、気になった方は是非くわしく調べてみてください。
おまけ
ZFとはなにかについてちょっとだけ触れます。
ZFとは、概ね、「このような集合は存在することができる」というように、考えたい集合の存在を保証してくれるものです(もうちょっと正確に言うと、「このような対象については真面目な議論ができますよ」という保証ですかね)。
そこには「自然数の集合を考えることができる」みたいなことは書かれていません。ノリとしては、「空集合を考えていいですよ」みたいな感じです。
そんな、一見不自由そうなZFですが、次のようなことができます。
- 自然数(0,1,2,...)を「再現したなにか」を作れる。
- 自然数の和差積商を再現できる。
- つまり有理数や、その数列もつくれる。
また、現代数学の対象は、大体が「集合の言葉で定義」されています。言わせれば、「あらゆる概念は、集合・論理である」のです!抽象的な解析学とかをやればびっくりして腰が抜けると思います()
いかがだったでしょうか?ほんとうは直和だとか具体的な自然数の構成方法だとか、もっともっと集合について話したいことはあるのですが、はじめはこれくらいで十分でしょう。
特に集合の基本が分かれば論理的思考の役に立つはずです。また、写像が分かれば「順像法」「逆像法」の知見が深まることでしょう。
この記事を通して集合論及び大学数学に興味を持っていただけたならば、とても嬉しいです。では、またどこかで...
