量子力学における散乱問題　一次元系

散乱問題 一次元編

　電子や中性子、光子などの波動性を持つ粒子を対象に当てると、対象の特性を反映した散乱パターンが見られます。例えば金属中では電子が運動していますが、不純物に散乱されて特有の電子波パターンを示します。電子の散乱がしばしば起きることで電気抵抗が生じます。

　散乱波から対象ポテンシャルを求める問題を逆問題と言いますが、逆問題を解くには順問題の正しい理解が重要です。

　この記事では一次元系の散乱順問題を考察します。一般には三次元散乱の問題になりますが、三次元だろうと変数分離して一次元系に帰着させるので、三次元系の本質は一次元系が担っていると捉えることもできます。

もちろん、回転や角運動量など多次元系特有の現象もあるので、安易に次元を下げるわけにはいきません。

　方程式の世界では、粒子の波をシュレディンガー方程式、対象をポテンシャル関数で表現します。粒子と対象に斥力が生じていたら正、引力が生じていたら負の値を取ります。このポテンシャルは対象の形状を反映して有限の広がりを持っているのが普通ですが、一点に局在したポテンシャルによる散乱波を重ね合わせると、広がったポテンシャルによる散乱も表現可能です。なぜなら一点局在ポテンシャルであるデルタ関数の畳み込み和は、任意の関数を表現できるからです。デルタ関数型ポテンシャルを例に、散乱問題を定性的に考察してみましょう。

デルタ関型数ポテンシャルによる散乱

散乱問題の要素を以下のように簡略化します。

(1)一次元系
(2)定常状態
(3)ポテンシャルは一点に局在
(4)平面波$e^{ikx}$を入射すると、透過波$Te^{ikx}$と反射波$Re^{-ikx}$が出力される。

$k$は粒子の波数として、$\hat{g} := \frac{2mg}{\hbar^2} $, $k^2 := \frac{2mE}{\hbar^2}$と整理してあげましょう。移項して整理すると、

$$\frac{d^2\psi(x)}{dx^2}+k^2\psi(x)=\hat{g}\delta(x)\psi(x)$$

ヘルムホルツ方程式に似てると思った人は、よく勉強している証拠です。

両辺微小区間$[-\varepsilon, \varepsilon]$で積分してあげます。波動関数は連続なので、左辺第二項は$\varepsilon\rightarrow 0$の極限で消えます。

$$\frac{d\psi(+0)}{dx}-\frac{d\psi(-0)}{dx}=\hat{g}\psi(0) \tag{1}$$

また、ポテンシャル部分でも波動関数は連続なので、

$$\psi(+0)-\psi(-0)=0 \tag{2}$$

(1)(2)が二つの境界条件になります。

1.1 左側から入射する場合、

(4)の仮定を使って状況を簡略化します。

(4)平面波$e^{ikx}$を入射すると、透過波$Te^{ikx}$と反射波$Re^{-ikx}$が出力

$$ \psi(x) =\left\{ \begin{array}{l} Te^{ikx} & (x \ge 0) \\ e^{ikx} + Re^{-ikx} & (x < 0) \end{array} \right. $$

(1)(2)の二つの境界条件より、

$$ \left\{ \begin{array}{l} ikT-ik(1-R)=\hat{g}\psi(0)=\hat{g}T \\ T = 1 + R \\ \end{array} \right. $$

(1)の境界条件において、$\psi(0) = 1 + R = T$を代入し忘れないよう注意しましょう。(著者は一敗済み)

整理すると、
$$ \left\{ \begin{array}{l} (1-\frac{\hat{g}}{ik})T+R=1 \\ T = 1 + R \\ \end{array} \right. $$
これを解いて、
$$T = \frac{1}{1-\frac{\hat {g}}{2ik}}, \ \ R = \frac{\frac{\hat {g}}{2ik}}{1-\frac{\hat {g}}{2ik}}$$

を得ます。$T$の分だけ透過するし、$R$の分だけ反射されます。

解釈

透過率や反射率は複素数なので、位相の変化も同時に生じます。斥力による散乱$g>0$を考えると、

$$Te^{ikx} = \frac{1}{1+\frac{\hat {g}^2}{4k^2}}\left[1-i\frac{\hat {g}}{2k}\right]e^{ikx}$$→ 虚部が負　→　位相が負にずれる　→ 波が正の方向にずれる

ことがわかります。ポテンシャルに電子波が押し除けられている様子が再現できます。

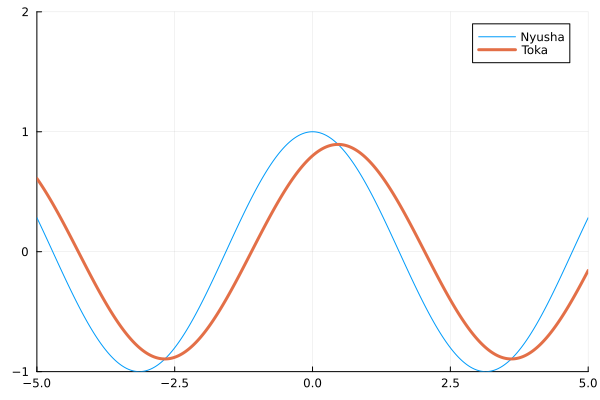入射波(青色)と透過波(赤色)の実部の関係

この図では敢えて$g$を小さく取り、頂点のズレが比較しやすいようにしました。頂点が進行方向に押し除けられて、位相が前にずれることを反映しています。

反射波についても同様に、

$$Re^{ikx} = \frac{1}{1+\frac{\hat {g}^2}{4k^2}}\left[-\frac{\hat {g^2}}{4k^2}-i\frac{\hat{g}}{2k} \right]e^{ikx}$$ 虚部が負　→　位相が負にずれる　→ 波が正の方向にずれる
ことがわかり、先ほどと同様の関係を得られます。

入射波と反射波の関係

1.2 右向きから入射する場合

(4)の仮定を逆向きに焼き直します。

(4)平面波$e^{-ikx}$を入射すると、透過波$T'e^{-ikx}$と反射波$R'e^{ikx}$が出力

$$ \psi(x) =\left\{ \begin{array}{l} e^{-ikx} + R'e^{ikx} & (x \ge 0) \\ T'e^{-ikx} & (x < 0) \end{array} \right. $$

(1)(2)の二つの境界条件から同様に求まりますが、後ほどもう少し簡単な方法で、$T' = R$, $R'=T$を示すことができます。

1.3 両方向から侵入する場合

同様に計算できるものの、係数の解釈を少し変えてみましょう。両側から進行する波のうち、ポテンシャルの向きに侵入する波を$a_{-}^{in}, a_{+}^{in}$、ポテンシャルから出ていく波を$a_{-}^{out}, a_{+}^{out}$で表現します。

境界条件(1)(2)を加味すると、4つの係数が2本の連立方程式で立式できるため、以下のような行列表記が可能になります。

$$\left( \begin{array}{c} a_{-}^{out} \\ a_{+}^{out} \end{array} \right) = \begin{pmatrix} S_{11} & S_{12} \\ S_{21} & S_{22} \end{pmatrix} \left( \begin{array}{c} a_{+}^{in} \\ a_{-}^{in} \end{array} \right) $$

$$ \psi(x) =\left\{ \begin{array}{l} a_{+}^{in} e^{-ikx} + a_{+}^{out} e^{ikx}& (x \ge 0) \\ a_{-}^{in} e^{ikx} + a_{-}^{out} e^{-ikx} & (x < 0) \end{array} \right. $$
この行列のことをS行列と呼んでいます。

S行列。下から上に時系列が流れていると解釈すると、
$a_{+}^{in}$が$a_{-}^{out}$に出力されると解釈できる。

境界条件を元に行列要素を決定すると、

$$ \left\{ \begin{array}{l} (-ika_{+}^{in}+ika_{+}^{out})-(ika_{-}^{in}-ika_{-}^{out}) = g\psi(0) \\ a_{-}^{in} + a_{-}^{out} = a_{+}^{in} + a_{+}^{out} = \psi(0) \\ \end{array} \right. $$

$$ \left( \begin{array}{c} a_{+}^{in} \\ a_{-}^{in} \end{array} \right) = \left( \begin{array}{c} A \\ B \end{array} \right) $$
とみなして、$a_{+}^{out}$と$a_{-}^{out}$について解くと見通しが良くなります。

$$ \left\{ \begin{array}{l} (-ikA+ika_{+}^{out})-(ikB-ika_{-}^{out}) = g\psi(0) \\ B + a_{-}^{out} = A + a_{+}^{out} \\ \end{array} \right. $$

連立方程式を解くと、

$$ \left\{ \begin{array}{l} a_{-}^{out} = A + \frac{\hat{g}}{2ik}(B + a_{-}^{out})\\ a_{+}^{out} = B + \frac{\hat{g}}{2ik}(A + a_{+}^{out})\\ \end{array} \right. $$

故に、行列要素が以下のように決定されます。

$$ \left\{ \begin{array}{l} a_{-}^{out} = \frac{1}{1-\frac{\hat{g}}{2ik}}a_{+}^{in} + \frac{1}{1-\frac{\hat{g}}{2ik}}\frac{\hat{g}}{2ik}a_{-}^{in}\\ a_{+}^{out} = \frac{1}{1-\frac{\hat{g}}{2ik}}\frac{\hat{g}}{2ik}a_{-}^{in} + \frac{1}{1-\frac{\hat{g}}{2ik}}a_{+}^{in} \\ \end{array} \right. $$

S行列を具体的に書くと、

$$S =\left( \begin{matrix} \frac{1}{1-\frac{\hat{g}}{2ik}} & \frac{1}{1-\frac{\hat{g}}{2ik}}\frac{\hat{g}}{2ik} \\ \frac{1}{1-\frac{\hat{g}}{2ik}}\frac{\hat{g}}{2ik} & \frac{1}{1-\frac{\hat{g}}{2ik}} \end{matrix} \right)$$

となります。

(1.2)で軽く紹介した逆向き散乱を考えたくば、係数を
$$a_{+}^{in} = 1 , \ \ a_{-}^{in} = 0$$
とおけば良いのです。

$$T' = a_{-}^{out} = \frac{1}{1-\frac{\hat{g}}{2ik}}\frac{\hat{g}}{2ik}, \ \ R' = a_{+}^{out} = \frac{1}{1-\frac{\hat{g}}{2ik}}$$

が導かれます。

1.4　S行列のユニタリー性

高度な内容なので、初見で理解する必要はありません

ポテンシャル関数が$x=0$について線対称なので、固有関数は奇関数と偶関数に分類できます。これを反映して、S行列を対角化すると、対角化する基底関数が偶関数と奇関数になります。それぞれ偶パリティ散乱と奇パリティ散乱と呼んでおきましょう

入射波と散乱波で粒子数は保存するので、S行列はユニタリーです。

$$|a_{-}^{in}|^2 + |a_{+}^{in}|^2=|a_{-}^{out}|^2 + |a_{+}^{out}|^2$$

を行列で表せば示せます。

ユニタリ行列の固有値は絶対値1の複素数であり、$e^{2i\delta_l}(l = 0,1)$と表現できます。対角化する行列が以下の行列$U$であることが容易に示せます。

$$U = \frac{1}{\sqrt{2}}\left( \begin{matrix} 1 &1 \\ -1 & 1 \end{matrix} \right)$$

この時、S行列は

$$S = U^{\dagger} \left( \begin{matrix} e^{2i\delta_1} &0 \\ 0 &e^{2i\delta_1} \end{matrix} \right) U =e^{i(\delta_0 + \delta_1)} \left( \begin{matrix} \cos(\delta_0-\delta_1) &i\sin(\delta_0-\delta_1) \\ i\sin(\delta_0-\delta_1) &\cos(\delta_0-\delta_1) \end{matrix} \right) $$

となり、固有値の指数部分が位相のずれを表現していることがわかります。特に、偶パリティと奇パリティで位相のズレが異なることは直感的には理解し難いので、S行列を数学的に料理して初めて得られる考察だと思います。

固有値の導出

S行列の固有値は以下のように求められます。

$$\det \left( \begin{matrix} \frac{1}{1-\frac{\hat{g}}{2ik}}-\lambda & \frac{1}{1-\frac{\hat{g}}{2ik}}\frac{\hat{g}}{2ik} \\ \frac{1}{1-\frac{\hat{g}}{2ik}}\frac{\hat{g}}{2ik} & \frac{1}{1-\frac{\hat{g}}{2ik}} -\lambda \end{matrix} \right) =　\left(\frac{1}{1-\frac{\hat{g}}{2ik}}-\lambda \right)^2 - \left(\frac{1}{1-\frac{\hat{g}}{2ik}}\frac{\hat{g}}{2ik}\right)^2 $$

$$ =\left(\frac{1}{1-\frac{\hat{g}}{2ik}} - \frac{1}{1-\frac{\hat{g}}{2ik}}\frac{\hat{g}}{2ik}-\lambda \right) \left(\frac{1}{1-\frac{\hat{g}}{2ik}} + \frac{1}{1-\frac{\hat{g}}{2ik}}\frac{\hat{g}}{2ik}-\lambda \right) = 0 $$

故に固有値は
$$\lambda = 1,\ \ \ \ \frac{1+\frac{\hat{g}}{2ik}}{1-\frac{\hat{g}}{2ik}}$$
より、位相のズレが以下のように計算できる。
$$\delta_0 = 0,\ \ \ \tan(\delta_1) = \frac{-\frac{\hat{g}}{k}}{1-\frac{\hat{g}^2}{4k^2}}$$

$g = 1$の時の位相のズレ

位相の式は分母＝0の点で発散します。発散の境界を挟んで、順位相と逆位相が切り替わることが見て取れます。

1.5　S行列の極についての考察

S行列の固有値はそれぞれ

$$\lambda = 1,\ \ \ \ \frac{1+\frac{\hat{g}}{2ik}}{1-\frac{\hat{g}}{2ik}}$$

であり、波数が実数の時には絶対値が１の複素数になるのした。今度は波数を複素数に拡張してみましょう。

固有値$e^{2i\delta_l}$が以上の拡張により、$\delta $が複素数になる状況を含むようになります。固有値は

$$e^{2i(u + vi)} = e^{-2v} e^{2iu}$$

より$v>0$ならば絶対値が減衰し、$v<0$ならば絶対値が増大します。遠方で振幅が膨れ上がる状況は非物理的なので除外します($Im(\delta)>0$の時のみ考える)。

複素位相での固有値の結果は、出力された波の振幅が遠方で減衰している状況に対応していると捉えることができます。そして、波が遠方で減衰しており、ポテンシャル近傍で値を持つ状況は、量子力学の世界で束縛状態と呼ばれるのでした。

束縛状態を持つには、ポテンシャルと粒子が引力相互作用を持つ$g<0$のときを考えれば良いでしょう。$g<0$のときの$k$の値で、最も特別な状況を表しているのは、固有値

$$\lambda =\frac{1+\frac{\hat{g}}{2ik}}{1-\frac{\hat{g}}{2ik}}$$

の分母がゼロになる状況です。そこで、固有値が極を取る時のエネルギーを求めてみます。

$$k = -i \frac{\hat{g}}{2}$$
より、エネルギーは
$$E = \frac{\hbar^2k^2}{2m}=-\frac{\hbar^2\hat{g}^2}{8m}=-\frac{mg^2}{2\hbar^2}$$

となります。この値は、デルタ型ポテンシャルの束縛状態のエネルギーの値と確かに一致します。

境界条件からデルタ型ポテンシャルの基底状態のエネルギーを求めることで、確かにこの値は導出できます。ですが、S行列の固有値の極から束縛状態のエネルギーを求められる保証は今の所ありません。

書籍を漁りまくっても文献が見つからなかった

最後に

勢いに任せて執筆したはいいものの、なんとも後味悪い最後を迎えてしまいました。JJ.Sakuraiにデルタ関数型ポテンシャルの束縛状態を求める演習問題を昔経験したことがあったので、極の端数が束縛状態にそっくりだという洞察ができました。

S行列時体は素粒子論や場の量子論でも登場する概念なので、極の分布が束縛状態や散乱状態、基底状態などの情報を担ってたら確かにアツい気もします。

「S行列の固有値が極がどのような物理的状況に対応するだろうか」

という疑問を、未来の自分に託します。

無責任とも呼びます