フォイエルバッハ点のとある性質の証明
今回の記事では, Emelyanov’s Theorem をオイラー・ポンスレ点と直角双曲線を用いて証明する.
次の補題が本質的である.
垂心系を成さない四点$A, B, C, P$のオイラー・ポンスレ点を$X$としたとき, $P$の三角形$ABC$における cevian circle は$X$を通る.
四点$A, B, C, P$を通る直角双曲線を$\mathcal{H}$とする. 有名事実として三角形$ABC$の九点円は$\mathcal{H}$の中心を通る. 同様にして, 三角形$BCP, CAP, ABP$の九点円は$\mathcal{H}$の中心を通る. よって, $\mathcal{H}$の中心は$X$に一致する. ここで, $P$の三角形$ABC$における cevian triangle を$DEF$としたとき, 前回の記事 の補題 3 より三角形$DEF$の内心と傍心は$\mathcal{H}$上にある. 傍心三角形の九点円はもとの三角形の外接円に一致するので, 円$DEF$が$X$を通ることが示された.
三角形$ABC$において, フォイエルバッハ点を$Fe$, 角の二等分線と対辺の交点をそれぞれ$D, E, F$とする. このとき, 四点$Fe, D, E, F$は共円である.
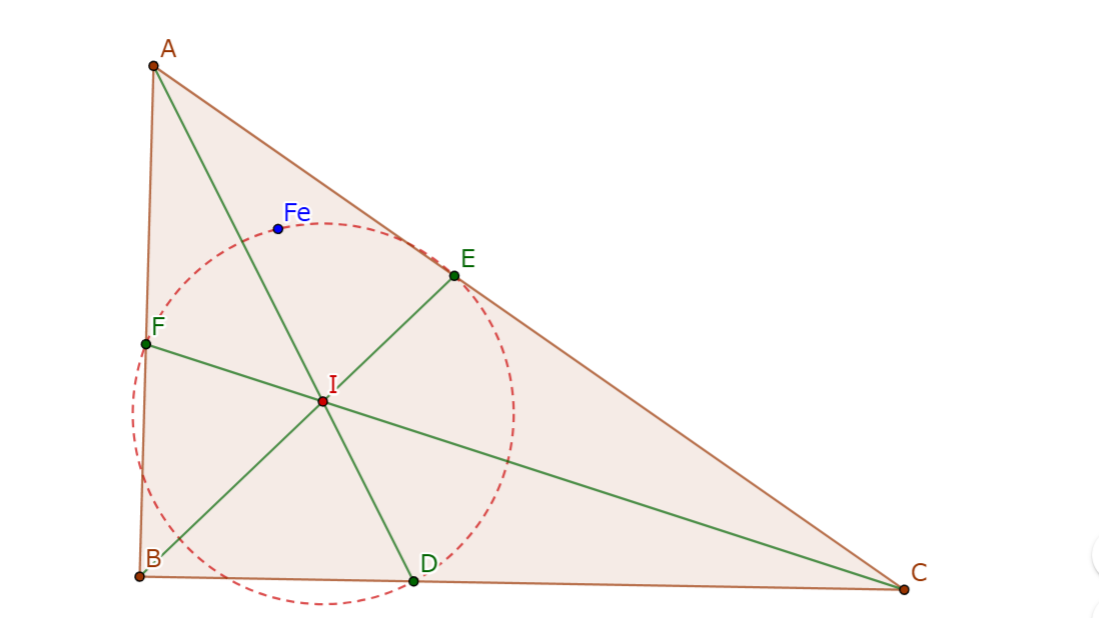
フォイエルバッハ双曲線を$\mathcal{H}$とする. 有名事実として$\mathcal{H}$の中心は$Fe$であり, また, 四点$A, B, C, I$のオイラー・ポンスレ点は$Fe$に一致する. よって, 四点$A, B, C, I$に補題 1 を適用することで示された.
この定理を用いると, 次のような性質を示すことができる.
三角形$ABC$において, 角の二等分線と対辺の交点を$DEF$とし, 外フォイエルバッハ点を$Fe_A, Fe_B, Fe_C$とする. このとき, 三角形$DEF$と三角形$Fe_AFe_BFe_C$は相似である.
内接円, $\angle A$-傍接円, 九点円に monge's theorem を適用することで, 三点$Fe, D, Fe_A$の共線を得る. 同様にして, 三点$Fe, E, Fe_B$, 三点$Fe, F, Fe_C$は共線である. すると,
定理 2 より, $\angle DEF = \angle DFeF = \angle Fe_AFeFe_C = \angle Fe_AFe_BFe_C$.
同様にして$\angle EFD = \angle Fe_BFe_CFe_A$なので示された.