(ネタ記事) 2^{2027}-1は素数か.
本題
稀に見るネタ記事です.
$2^{2027}-1$は素数か.
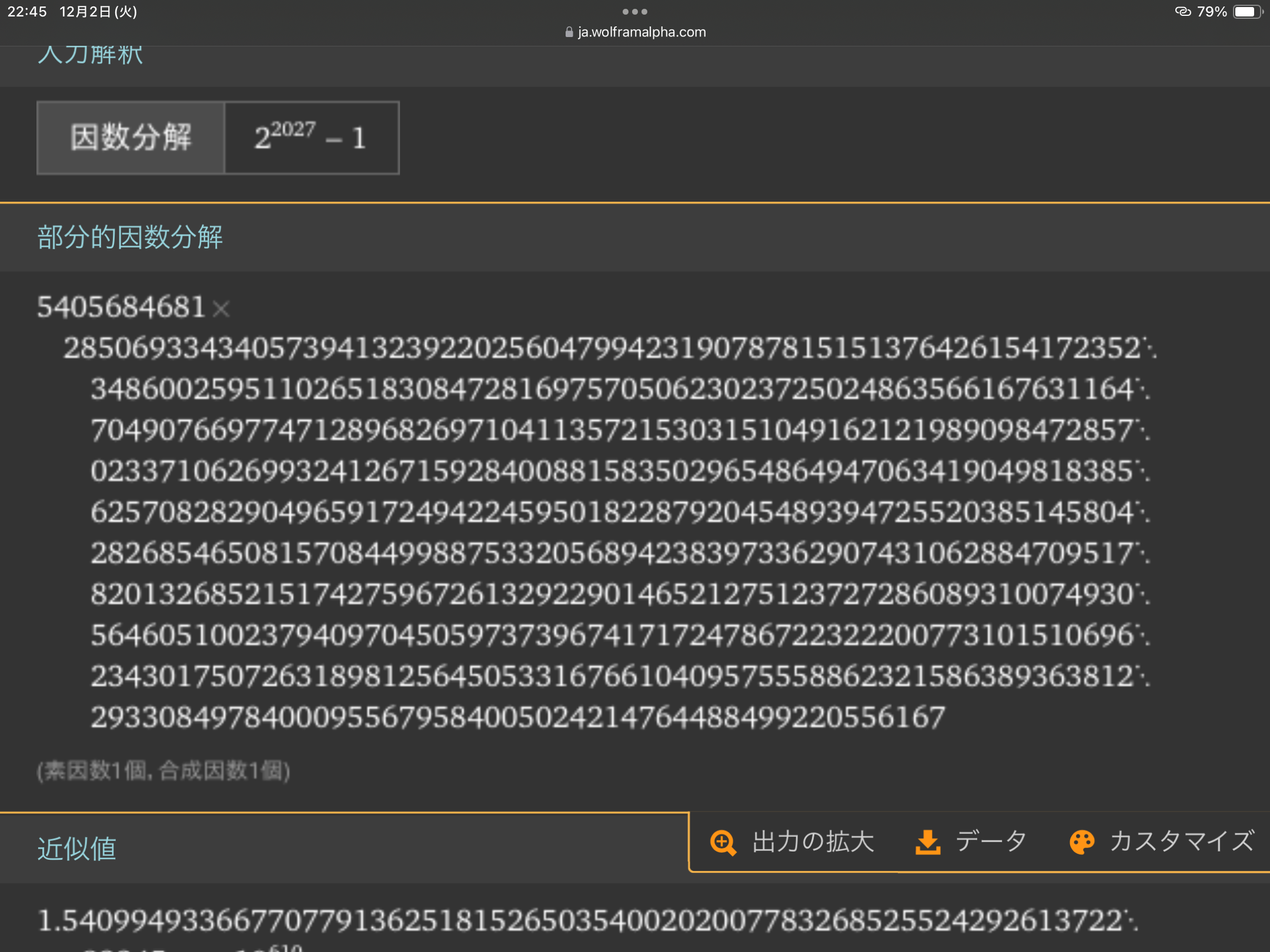
最小の素因数で因数分解をすると,
$5405684681×
285069334340573941323922025604799423190787815151376426154172352
3486002595110265183084728169757050623023725024863566167631164
7049076697747128968269710411357215303151049162121989098472857
0233710626993241267159284008815835029654864947063419049818385
6257082829049659172494224595018228792045489394725520385145804
2826854650815708449988753320568942383973362907431062884709517
8201326852151742759672613292290146521275123727286089310074930
5646051002379409704505973739674171724786722322200773101510696
2343017507263189812564505331676610409575558862321586389363812
29330849784000955679584005024214764488499220556167$
となって素数ではない.
(訂正済み)
あとがき
 ふ ざ け ん な
ふ ざ け ん な
ちゃんとした方の記事も後々あげます.
では次の記事でお会いしましょう.
