数列のチェザロ平均の集積点~学部で習うあの事実の一般化~
ごあいさつ
はじめまして, Torteです. 微分幾何学や解析学が好きなので, それらに関連した話題をこれから書き散らしていけたらと考えております.
今回は数列の集積点についてのお話です. 学部生だった頃に解けなかった上下極限の練習問題のひとつなのですが, 主張自体が面白い割に解説を見かけたことがなかったため, 過去の自分に宛てるつもりでこの度記事を書いてみることにしました.
※本稿では数列の上下極限, および集積点の知識を仮定します. また, 数列は全て実数列とします.
数列のチェザロ平均
数列$\{a_n\}_n$の第$n$項までの平均$\displaystyle s_n=\frac{1}{n}\sum_{j=1}^{n}a_j$を, 数列$\{a_n\}_n$のチェザロ平均といいます. チェザロ平均に関しては, 理系大学生であればおそらく学部1年で習う次の事実が有名でしょう.
数列$\{a_n\}_n$が$\displaystyle \lim_{n \to \infty}a_n = \alpha$を満たすならば, そのチェザロ平均$\{s_n\}_n$も$\displaystyle \lim_{n \to \infty}s_n = \alpha$をみたす.
この事実は, 大学数学最初の難所である$\varepsilon$-$N$論法の練習問題としてお馴染みです(なので証明は割愛). 今回は収束するとは限らない数列$\{a_n\}_n$のチェザロ平均について考えてみましょう.
具体例の計算
数列が無限大に発散する場合には, 先の事実の証明と同様にして, チェザロ平均も無限大に発散することが確かめられます. ですので, 収束しない数列$\{a_n\}_n$としては有界なものを考えましょう.
収束しない有界数列の例としてパッと思いつくのは, 次のような振動する数列です.
数列$\{a_n\}_n$を$a_n = (-1)^n$で定義する. このとき, $\{a_n\}_n$のチェザロ平均$\{s_n\}_n$は
\begin{align}
s_n=
\begin{cases}
0 &\text{$n$が偶数のとき,}\\
\frac{1}{n} &\text{$n$が奇数のとき,}
\end{cases}
\end{align}
で与えられる. 特に$\displaystyle\lim_{n \to \infty}s_n = 0$である.
もう少し一般化して, 周期的な数列についても考えてみましょう.
数列$\{a_n\}_n$は周期$N$の数列とする. すなわち任意の自然数$n$に対し$a_{n+N} = a_n$が成り立つとする. このとき, $\alpha = (1/N)\sum_{j=1}^{N}a_j$とすると, $s_n \to \alpha$となる. 実際, 十分大きな$n$に対して, $n$を$N$で割った商を$q$, 余りを$r$とすると, 数列の周期性から,
\begin{align}
s_n = \frac{1}{n}\left(\underbrace{\sum_{j=1}^N a_j+\cdots+\sum_{j=1}^N a_j}_{\text{$q$個}}\right)+\frac{1}{n}\sum_{j=1}^{r}a_j= \frac{qN}{n}\alpha+\frac{1}{n}\sum_{j=1}^{r}a_j
\end{align}
となる.したがって, $\displaystyle A=\max_{1\leq j \leq N}|a_j|$とおくと, $n=qN+r$および$0 \leq r < N$に注意して,
\begin{align}
|s_n-\alpha|\leq \frac{r|\alpha|}{n}+\frac{rA}{n} \leq \frac{N(|\alpha|+A)}{n} \to 0
\end{align}
となって, $s_n \to \alpha$がわかる.
このように, 数列$\{a_n\}_n$自体が収束しなくても, そのチェザロ平均はある値に収束することがあります. そうすると今度は「チェザロ平均が発散するような有界数列はあるか?」という疑問が湧いてきます. そのような数列の例としては次のようなものがあります.
数列$\{a_n\}_n$を次のように定義する:
\begin{align}
a_n=
\begin{cases}
1 &\text{$2^{m-1}\leq n <2^m, m=1, 2, \ldots$のとき,}\\
0 &\text{$2^{m}\leq n <2^{m+1}, m=1, 2, \ldots$のとき.}
\end{cases}
\end{align}
すなわち$\{a_n\}_n$は$1, 0, 0, 1, 1, 1, 1, \ldots$のように,$n$が奇数のときは第$n$群を$2^{n-1}$個の$1$が並んだもの, $n$が偶数のときは第$n$群を$2^{n-1}$個の$0$が並んだものとして得られる群数列である.
自然数$m$に対し, 第$2m$群までの$2^{2m+1}-1$項分のチェザロ平均を計算すると,
\begin{align}
s_{2^{2m+1}-1} = \frac{1+4+\cdots+4^m}{1+2+\cdots+2^{2m}}
= \frac{1}{3}\cdot \frac{4^{m+1}-1}{2\cdot4^m-1} \to \frac{2}{3}
\end{align}
となる. 一方, 第$2m+1$群までのチェザロ平均は同様にして$\displaystyle \frac{1}{3}$に収束することが示せる. こうして, 異なる値に収束する二つの部分列が取れたので, この数列のチェザロ平均$\{s_n\}_n$は収束しないことがわかった.
この例についてもう少し見てみましょう. 例3では「キリのいい」ところで項を打ち切った部分列を考えていたので, 今度は項をもう少し加えた部分列を計算してみます.
数列$\{a_n\}_n$を例3で扱った数列とする. $m$を自然数として, 第$2m+1$群の第$2^{2m}$項(すなわち第$2m$群に$0$を$2^{2m}$個加えたもの)までのチェザロ平均を計算すると,
\begin{align}
\frac{1+4+\cdots+4^m}{1+2+\cdots+2^{2m}+2^{2m}}
= \frac{1}{3}\cdot \frac{4^{m+1}-1}{3\cdot4^m-1} \to \frac{4}{9}
\end{align}
となる. 同様に, 第$2^{2m+2}$群の第$2^{2m+1}$項までのチェザロ平均の極限は$5/9$となる. 特に, これらの値は区間$[1/3, 2/3]$に属する.
部分列の取り方を色々変えてみると, $1/3$から$2/3$までのさまざまな値を実現できることが確認できます.
例3での計算から, $2/3$は分子にできるだけ$1$を含むようにして作った「値の大きい」部分列の極限なので, これはチェザロ平均$\{s_n\}_n$の上極限だと考えられます. 同様に, $1/3$はチェザロ平均$\{s_n\}_n$の下極限だと考えられます. これを踏まえると例4は, 部分列の取り方を工夫することで, 下極限$1/3$から上極限$2/3$までの実数を, チェザロ平均の集積点として実現でき得ることを示唆している…という風にも見ることができそうです.
有界数列のチェザロ平均の集積点
以上を踏まえて, 本稿のメインテーマに移ります. 先の例で見た通り, チェザロ平均そのものが収束しない場合でも, 集積点全体を考えることには何か意味がありそうです.
実は収束するとは限らない有界数列に関しては, 冒頭に挙げた事実の次のような一般化が成立します.
数列$\{a_n\}_n$は有界であるとする. このとき, $\{a_n\}_n$のチェザロ平均のなす数列$\{s_n\}_n$の集積点全体は区間$\displaystyle \left[ \liminf_{n \to \infty} s_n, \limsup_{n \to \infty} s_n\right]$と一致する.
証明のアイデア
証明に入る前に, 少しだけイメージを述べておきましょう.
まず, 集積点の定義について復習しておきます.
$1$次元Euclid空間$\mathbb{R}$の部分集合$A \subset \mathbb{R}$に対し, 点$x \in \mathbb{R}$が$A$の集積点(accumulation point)であるとは, 任意の$\varepsilon>0$に対してある$a \in A\setminus \{x\}$が存在して, $|a-x| < \varepsilon$が成り立つようにできることをいう.
つまり, 集積点$x$の周りには($x$以外の)$A$の点が無数に存在する, というイメージです. 数列の上極限や下極限も, 数列の要素のなす集合の集積点の一種です.
上極限や下極限はそれぞれ集積点集合の最大値および最小値ですから, 集積点集合が考えている区間に含まれていることは明白です. ですので後は, 区間内の任意の点の周りに$s_n$が無数に存在することが言えれば良いわけです.
少なくとも区間の端点の周りには無数の$s_n$が存在しているのですから, $s_n$たちは「端から端までジャンプ」することを無限回繰り返していることになります. ジャンプ一回分の歩幅$|s_{n+1}-s_n|$がもし小さければ, 区間上には端から端まで移動する際についた沢山の足跡が残ることになります. ステップ数$n$が大きくなるにつれて歩幅も小さくなることが言えれば, 区間はこの足跡, すなわち$s_n$たちで埋め尽くされることになり, これにより主張が示せそうです.
![数列!FORMULA[97][67506229][0]が集積するイメージ](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FBiaHogiYLSDeEZKEe0Ab.jpg?alt=media)
数列$\{s_n\}_n$が集積するイメージ
実際に集積点であることを示そうとすると, 部分列を具体的に構成する必要があって少し骨が折れるので, 今回は上記のイメージをもとに背理法で証明することにします. 結論を否定すると「飛び越えないといけない大穴が出現するが, 歩幅が小さすぎて飛び越えられない」というイメージが浮かぶので, そのことを数学の言葉で記述します.
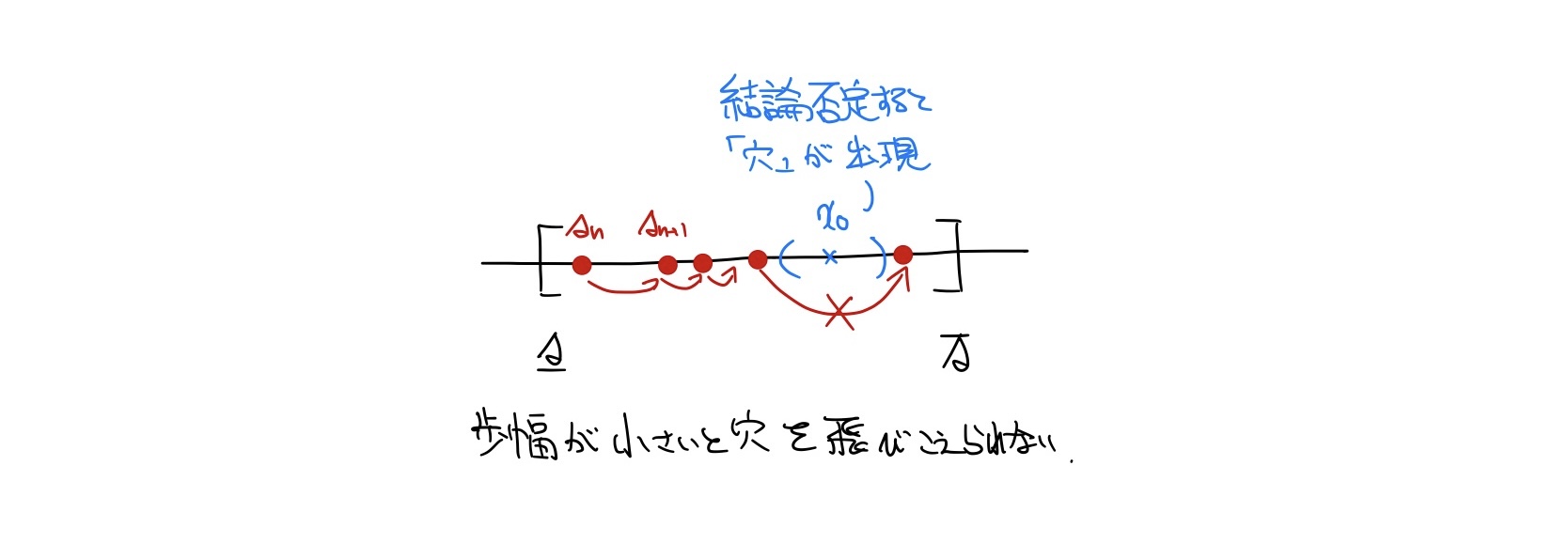背理法による証明のイメージ
数列$\{s_n\}_n$の集積点全体のなす集合を$S$とする. また, $\displaystyle \underline{s}=\liminf_{n \to \infty}s_n$, $\displaystyle \overline{s}=\limsup_{n \to \infty}s_n$とおく. $\underline{s}=\overline{s}$のときは主張の成立は明らかなので, $\underline{s}<\overline{s}$とする.
上下極限の定義から$\overline{s}=\max{S}$, $\underline{s}=\min{S}$となるので. $S \subset [\underline{s}, \overline{s}]$である.
そこで, $S \neq [\underline{s}, \overline{s}]$と仮定する. すなわち, ある$x_0 \in (\underline{s}, \overline{s})$と正の実数$\varepsilon_0>0$があって, 任意の自然数$n$に対し$|s_n-x_0| \geq \varepsilon_0$が成り立つとする.
数列$\{a_n\}_n$は有界なので, ある正の実数$M>0$があって, 任意の自然数$n$に対し$|a_n| \leq M$とできる. このとき,
\begin{align}
|s_n| \leq \frac{1}{n} \sum_{j=1}^{n}|a_j| \leq \frac{1}{n} nM=M
\end{align}
より$|s_n| \leq M$となる.
ここで,
\begin{align}
s_{n+1}=\frac{1}{n+1}\sum_{j=1}^{n+1}a_j=\frac{1}{n+1}\sum_{j=1}^{n}a_j+\frac{a_{n+1}}{n+1}=\frac{n}{n+1}s_n+\frac{a_{n+1}}{n+1}
\end{align}
となるので,
\begin{align}
|s_{n+1}-s_n|=\left|\frac{-s_n}{n+1}+\frac{a_{n+1}}{n+1}\right| \leq \frac{|s_n|+|a_{n+1}|}{n+1} \leq \frac{2M}{n+1}.
\end{align}
そこで, 自然数$N$を$2M/(N+1)<\varepsilon_0$となるよう十分大きく取っておくと, $n>N$ならば$|s_{n+1}-s_n|<\varepsilon_0$とできる.
いま, $\varepsilon>0$を十分小さく取って, $\underline{s}+\varepsilon < x_0-\varepsilon_0$および$x_0+\varepsilon_0 < \overline{s}-\varepsilon$が成り立つようにしておく(区間の端点のごく近辺だけを考えたいため).
$\underline{s}$や$\overline{s}$は$S$の元だから, 自然数$N_{-}$および$N_{+}$が存在して, $|s_{N_{-}}-\underline{s}|<\varepsilon$および$|s_{N_{+}}-\overline{s}|<\varepsilon$が成り立つようにできる. このような$N_{-}$や$N_{+}$は無限に存在するので, 必要なら大きく取り直して, $N< N_{-}< N_{+}$と仮定してよい. このとき, 有限点列$\{s_n\}_{n=N_{-}}^{N_{+}}$は, 集合$[\underline{s}-\varepsilon, x_0-\varepsilon_0]\cup[x_0+\varepsilon_0, \overline{s}+\varepsilon]$に含まれる. さらに, $s_{N_{-}}\in [\underline{s}-\varepsilon, x_0-\varepsilon_0]$, $s_{N_{+}}\in [x_0+\varepsilon_0, \overline{s}+\varepsilon]$だから, $N_{-} \leq n < N_{+}$を満たすある自然数$n$に対し,
\begin{align}
|s_{n+1}-s_n| \geq 2\varepsilon_0
\end{align}
が成り立つ必要がある(どこかで大ジャンプが必要).
ところがこの$n$は$n>N$を満たすから, $|s_{n+1}-s_n|<\varepsilon_0$でなければならず(大ジャンプできるだけの歩幅がない!), 矛盾する.
以上により, $S=[\underline{s}, \overline{s}]$が成り立つ.
こうして, 収束しない有界数列に対しても, 極限ではなく集積点を考えることで, チェザロ平均を「収束させる」ことが可能になることがわかりました.
有名な事実でも, ちょっぴり深掘りしてちょっぴり一般化できると, ちょっぴり嬉しい. そんな数学特有の楽しみを, 本記事を通して少しでも感じていただければ幸いです.
この記事を高評価した人
この記事に送られたバッジ
投稿者
