じゃんけんの期待回数について

$n\gt1$のとき、マルコフ性より、
\begin{equation} \begin{split} &E(n)= \sum_{i=1}^{n}p(n,i)(E(i)+1) \\ &\Longleftrightarrow(1-p(n,n))E(n)=1+\sum_{i=1}^{n-1}p(n,i)E(i)(\because\sum_{i=1}^{n}p(n,i)=1) \end{split} \end{equation}
$p(n,n) \neq$$1$　として
\begin{equation} \begin{split} E(n)=\frac{1}{1-p(n,n)}(1+ \sum_{i=1}^{n-1}p(n,i)E(i))\end{split}\end{equation}を得る。

$a$$\gt$$b$のときは略
$a=b$のとき、$p(a,b)$はつまりあいこになる確率。
\begin{equation} \begin{split} p(a,a)&=1-\sum_{i=1}^{a-1}p(a,i) \\ &=1-\sum_{i=0}^{a} \frac{1}{ 3^{a-1}}\binom{a}{i}+\frac{2}{3^{a-1}} \\ &=1-\frac{2^{a}-2}{3^{a-1}} \end{split} \end{equation}
よって、補題１より、$E(n)$の漸化式を得る。

https://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1205-9.pdf
をご参照ください。
補題２で得られた漸化式を用いて帰納的に証明できます。
具体的な形は
$\dfrac{1}{3}(\dfrac{3}{2})^{n} \leq E(n)$$\leq$ $(\dfrac{3}{2})^{n}$
です。

$a \gt b$のとき　略
$a=b$のとき、つまりあいこになる確率は、参加者が全員王様に勝利するか、全員あいこor負けとなる確率なので、
$p(a,a)=(\dfrac{2}{3})^{a}+(\dfrac{1}{3})^{a}$
よって、補題１より$K(n)$の漸化式を得る。

①$K(n)=O(\log_{3}{n})$ の証明

$\forall n$$\in$$\mathbb{N}$について$K(n) \leq an+b$ と仮定する。($a,b=const.$)
このとき補題４より、1より大きい自然数$n$に対し
\begin{equation} \begin{split} K(n)&=\dfrac{1}{3^{n}-2^{n}-1}(3^{n}+\sum_{i=1}^{n-1}2^{n-i}\dbinom{n}{i}K(i)) \\ &\leq \dfrac{1}{3^{n}-2^{n}-1}(3^{n}+\sum_{i=2}^{n-1}2^{n-i}\dbinom{n}{i}(ai+b)) \\ &=\dfrac{1}{3^{n}-2^{n}-1}(3^{n}+\sum_{i=0}^{n}2^{n-i}\dbinom{n}{i}(ai+b)-(an+b)-2^{n-1}(a+b)n-2^{n}b) \\ &=\dfrac{1}{3^{n}-2^{n}-1}(3^{n}+3^{n-1}an+3^{n}b-(an+b)-2^{n-1}(a+b)n-2^{n}b) \\ &=\dfrac{1}{3^{n}-2^{n}-1}(3^{n}+an(3^{n-1}-2^{n-1}-1)+b(3^{n}-2^{n}-1)-2^{n-1}bn) \\ &=\dfrac{1}{3^{n}-2^{n}-1}(3^{n}+\dfrac{an}{3}(3^{n}-2^{n}-1)+b(3^{n}-2^{n}-1)-\dfrac{2^{n}}{6}an-\dfrac{2}{3}an-2^{n-1}b) \\ &\leq \frac{1}{3}an+b+1 \end{split} \end{equation}
これを繰り返すことで、$\forall t \in \mathbb{N}$ に対し
$K(n)\leq (\dfrac{1}{3})^tan+t+b $が成り立つ。
よって　$t= \lceil \log_{3}{n}\rceil $　とおくと、
\begin{equation} \begin{split} K(n)&\leq(\dfrac{1}{3})^{\lceil \log_{3}{n}\rceil}an+\lceil \log_{3}{n}\rceil+b &\leq(\dfrac{1}{3})^{\log_{3}{n}}an+\log_{3}{n}+1+b \\ &=\log_{3}{n}+a+b+1 \end{split} \end{equation}
$K(n)\leq2n$であることは帰納法で簡単に示せるので、
$K(n)\leq \log_{3}{n}+3$
したがって　$K(n)=O(\log_{3}{n})$を得る。

②$K(n)= \Omega(\log_{3}{n}) $の証明
本筋は①と同じです。
$\forall n \in \mathbb{N} $に対して、
$K(n) \geq \dfrac{a}{n+1}+b $が成り立つと仮定する。このとき、1より大きい$n$について
\begin{equation} \begin{split} K(n)&=\dfrac{1}{3^{n}-2^{n}-1}(3^{n}+\sum_{i=1}^{n-1}2^{n-i}\dbinom{n}{i}K(i)) \\ &\geq\dfrac{1}{3^{n}-2^{n}-1}(3^{n}+\sum_{i=0}^{n}2^{n-i}\dbinom{n}{i}(\frac{a}{n+1}+b)-2^{n}(a+b)-(\frac{a}{n+1}+b)) \\ &\geq\dfrac{1}{3^{n}-2^{n}-1}(3^{n}+\frac{3^{n+1}a}{n+1}+3^{n}b-2^{n}(a+b)-(\frac{a}{n+1}+b)) \\ &=\frac{1}{3^{n}-2^{n}-1}(3^{n}+\frac{3a}{n+1}(3^{n}-2^{n}-1)+b(3^{n}-2^{n}-1)+\frac{3a \times 2^{n}}{n+1}+\frac{3a}{n+1}) \\ &= \frac{3a}{n+1}+b+\frac{(n+1)3^{n}+3a\times 2^{n}+3a}{(n+1)(3^n-2^n-1)} \\ &\geq\frac{3a}{n+1}+b+1 \end{split} \end{equation}
よって帰納的に$\forall t \in \mathbb{N} $に対して
$K(n)\geq\dfrac{a3^{t}}{n+1}+t+b$ を得る。
$t= \lceil\log_{3}{n}\rceil $とおくと、]
$K(n)\geq\log_{3}{(n+1)}+a+b$
$\forall n \in \mathbb{N} $ について
$K(n)\geq \dfrac{1}{n+1}-1$が成り立つことは簡単に示せるので、$a=1,　b=-1$　として
$K(n)\geq \log_{3}{(n+1)}\geq \log_{3}{n}$
したがって、　$K(n)= \Omega(\log_{3}{n}) $ を得る。
①、②より、
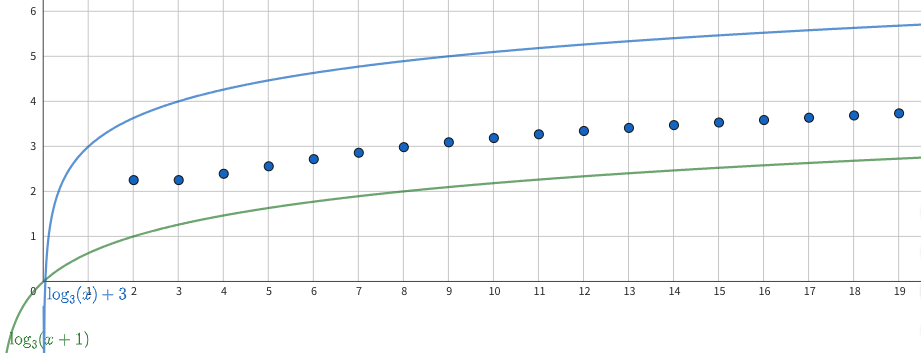
$\log_{3}{(n+1)}\leq K(n)\leq\log_{3}{n}+3$ $(n\geq2)$
すなわち$K(n)= \Theta(\log_{3}{n}) $　　　　　　（証明終）

$n$は１より大きい自然数とする。
\begin{equation} \begin{split} &\log_{3}{(n+1)}\leq K(n)\leq \log_{3}{n}+3 \\ &\iff \frac{\log_{3}{(n+1)}}{\log_{3}{n}}\leq \frac{K(n)}{\log_{3}{n}}\leq 1+\frac{3}{\log_{3}{n}} \\ \end{split} \end{equation}
$n \rightarrow ∞$で右辺と左辺は共に１に収束する。
よってハサミウチの原理より
\begin{split} \lim_{n \to \infty}\dfrac{K(n)}{\log_{3}{n}}=1 \end{split}

$n\geq7$のとき
$K(n)<\log_{3}{n}+3<\dfrac{1}{3}(\dfrac{3}{2})^n< E(n)$
なので、あとは$6$以下の$n$について調べることで系２を得る。